顾及障碍物的一般图形Voronoi图及其加权图的ArcGIS栅格实现

田松，崔希民，孙云华，崔伟宏，李文杰

（1.中国矿业大学（北京）地球科学与测绘工程学院，北京 100083；2.中国科学院遥感与数字地球研究所，北京 100101）

Voronoi图是一种对空间无缝不重叠的最短距离分割方法［1］，具有势力范围、侧向邻近、局域动态等特性［2，3］，成功解决了找最近点、求最大空圆、求n个点的凸包、求最小树等问题［4］，是计算几何的重要分支，广泛应用于物理、化学、分子生物、医学、地学等领域。在地学领域，Voronoi图可用于空间插值［5］、空间关系表达［6］、城市影响范围分析［7］、最优路径选取［8］、城市规划［9］、设施选址分析［10］等方面。

一般图形Voronoi图由普通Voronoi图生成元扩展为点、线、面而成，是对Voronoi图理论和应用的扩充，当前，该领域研究较为成熟。例如，张有会等［11］研究了一般图形Voronoi图的近似构造法；赵晔等［12］以距离表方式离散生成一般图形Voronoi图；曹清洁、安志宏、董雪等［13－15］先后研究了障碍物Voronoi图的离散生成及应用；Gong等［16］利用矢量方式生成了一般图形加权Voronoi图，并实现了点、线、面实体的插入和删除。关于一般图形Voronoi图与 GIS结合的应用研究，Dong［17］和范熙伟［1］分别以栅格方式和矢量方式结合GIS开发组件生成了点、线、面的Voronoi图及加权图，但二者算法均只能单独处理点、线、面生成元，限制了其应用范围，且未考虑障碍物情况。本文利用ArcEngine，以栅格结晶方式生成了顾及障碍物的一般图形Voronoi图及其加权图，该方法不需要考虑生成元形状，避免了计算Voronoi边界形状的大量计算，实现简单。同时与ArcGIS软件紧密结合，为研究和发展GIS空间数据结构和模型提供了重要方法。

1 基本定义

1.1 一般图形加权Voronoi图定义

定义1［11］：设p为平面上的点，G为平面上的几何图形，定义p和G之间的距离为：

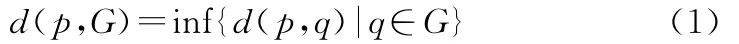
定义2：设Gi（i＝1，2，…，n）为平面上互不相交的几何图形，λi（i＝1，2，…，n）是给定的n个正实数，称V（Gi）是由生成元Gi确定的权重为λi的一般图形加权Voronoi图，当λ1＝λ2＝…＝λn时，V（Gi）为一般图形Voronoi图。

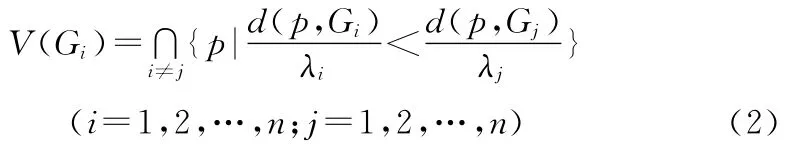
1.2 一般图形障碍加权Voronoi图定义

定义3［18］：设G为平面上互不相交的几何图形，O为平面上的线状或面状障碍物，p1、p2为平面上的两个点。若从任一目标点开始，到达另一目标点的路径不与障碍物集合O相交或仅与边界相交，则称此路径经过的最短欧氏距离为p1与p2的障碍距离，记为d0（p1，p2）。定义p和G 的障碍距离为：

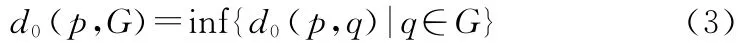
定义4：设Gi（i＝1，2，…，n）为平面上互不相交的几何图形，λi（i＝1，2，…，n）是给定的n个正实数，Oj（j＝1，2，3，…，m）为平面上的线状、面状障碍物，称V（Gi）是由生成元Gi确定的权重为λi的一般图形障碍加权Voronoi图，当λ1＝λ2＝…＝λn时，V（Gi）为一般图形障碍Voronoi图。

2 顾及障碍物的一般图形Voronoi图及其加权图结晶算法

2.1 算法的基本思想

所有被障碍物覆盖的栅格（记为障碍物栅格）赋予统一颜色值。所有被生成元覆盖的栅格（记为生成元栅格）指定相应颜色，保证不同生成元栅格之间颜色不同，同时与障碍物栅格颜色不同，赋予生成元栅格相应权重值。对于每类生成元栅格，选取边界栅格作为扩散中心，以指定规则向外结晶，并将结晶区域赋予同中心栅格相同的颜色。结晶过程中需检验：如果结晶区域已着色（包括已赋予其他类别生成元栅格颜色或障碍物栅格颜色），则越过；否则就以中心栅格对应的颜色着色结晶区域，当屏幕所有像素着色完成时，算法结束。这时，不同颜色区域间的边界即为Voronoi图的边界近似曲线。

图1 算法流程Fig.1 Algorithm flow chart

2.2 算法的实现步骤

输入：生成元集合Gi（i＝1，2，…，n），为平面上互不相交的任意几何图形，包含属性PointID：生成元Gi的唯一标识；Color：Gi颜色，Weight：Gi权重，Gi.Weight＝λi，障碍物集合Oj（j＝1，2，…，m）。

输出：一般图形Voronoi栅格图或加权栅格图VR（Gi）（i＝1，2，…，n）；一般图形 Voronoi矢量图或加权矢量图Vv（Gi）（i＝1，2，…，n）。

算法具体实现步骤如下：1）数据获取。从GIS矢量数据集中获取生成元集合Gi（i＝1，2，…，n），障碍物集合Oj（j＝1，2，…，m），保证任意生成元不重合，任意生成元与障碍物不重合；结晶速度集合Si（i＝1，2，…，n）；速度阈值thresh。2）生成Gi的最小外包矩形 MBR。3）栅格划分。设定栅格大小，将MBR划分为一系列正方形栅格集合Rk（k＝1，2，…，z），包括属性GridID：栅格Rk的唯一标识；PointID：生成元标识，拥有相同PointID的栅格为一类生成元栅格；Color：栅格颜色；CurrentSpeed：记录算法执行过程中的实时结晶速度；Original－Speed：记录原始结晶速度，该值恒定，由生成元权重确定；State：当前栅格状态，由Before、Now和Next 3种状态组成，分别表示栅格“已参与完操作”、“正参与操作”和“等待参与操作”。4）障碍物区域赋值。递归循环R，如果Rk∩Oj≠Φ，则令Rk.Corlor＝ζ，ζ为恒定正整数，表示该栅格为障碍物区域。5）生成元区域赋值。递归循环R，如果Rk∩Gi≠Φ，则令Rk.PointID＝Gi.PointID，Rk.Color＝Gi.Color，Rk.OriginalSpeed＝Si，Rk.CurrentSpeed＝Si，Rk.State＝Now。如果Rk∩Gi＝Φ，则令Rk.PointID＝－1，Rk.Color＝－1，Rk.OriginalSpeed＝－1，Rk.CurrentSpeed＝－1，Rk.State＝Next。6）区域结晶。递归循环R，如果Rk.State＝Now，同时Rk.PointID＞0，表示Rk是“正参与操作”的生成元栅格，可以参与结晶过程。如果选择一般图形障碍加权Voronoi结晶，则计算Rk结晶速度speed，speed＝Rk.Original－Speed＋Rk.CurrentSpeed，若speed＞thresh，按相应结晶规则获取Rk周围栅格Rq（q＝1，2，…，x），如果Rq.PointID＞0或Rq.Color＝ζ，说明该位置已经被填充，继续下一次递归；否则令Rq.PointID＝Rk.Point－ID，Rq.Color＝ Rk.Color，Rq.OriginalSpeed＝Rk.OriginalSpeed，Rq.CurrentSpeed＝speed－thresh，Rk.State＝Before。如果speed＜thresh，则令Rq.CurrentSpeed＝speed，继续下一次递归。如果选择一般图形障碍Voronoi图结晶，则按相应结晶规则获取Rk周围栅格Rq（q＝1，2，…，x），如果栅格Rq.PointID＞0或Rq.Color＝ζ，说明该位置已经被填充，继续下一次递归，否则令Rq.PointID＝Rk.PointID，Rq.Color＝ Rk.Color，Rk.State＝Before。7）状态更新。递归循环R，如果Rk.PointID＞0，同时Rk.State＝Next，令Rk.State＝Now。如果全部PointID＞0，算法结束，否则执行步骤6。8）数据输出。输出文件为一般图形Voronoi栅格图或加权栅格图VR，根据实际需要可以将其转化为矢量图或加权矢量图Vv，一并输出。

2.3 关于算法的几点说明

2.3.1 结晶规则 Voronoi图离散生成方式包括距离表法和结晶法等。由于结晶法模型众多，实现灵活，固选作本文算法的主要实现方式，可根据实际需要，选择相应结晶方式。常见结晶规则如下［13］：4－模板（图2a），生成元以菱形方式生长；8－模板（图2b），生成元以正方形方式生长；4－模板、8－模板交替（图2c），生成元以近似圆形方式生长。3种结晶规则分别对应数字图像中3种不同的距离度量方法［19］：

图2 图像结晶规则及距离度量方法［13］Fig.2 Image crystallization rule and distance measurement method

2.3.2 颜色的确定及边界提取 Gi的颜色属性可以是灰度值或RGB值，相应生成VR（Gi）灰度图或RGB图。算法执行前设定颜色方式，Color值为随机生成。在VR（Gi）生成后，通常需要标定不同类型生成元栅格间的Voronoi边，称为Voronoi边的近似抽出，其实质是栅矢转换的过程。在ArcEngine中，提供相关接口实现栅矢图转换。

2.3.3 结晶速度确定 算法结晶速度确定如下：

由式（8）和式（9）可知：Si的最大值为1。

根据2.2步骤（6）给出的公式：Rk.OriginalSpeed＝Si，Rk.CurrentSpeed＝Si，speed＝Rk.OriginalSpeed＋Rk.CurrentSpeed。令thresh＝1，判断栅格Rk扩张的条件是如果speed＞1，则扩张，Rk.CurrentSpeed＝speed－1；否则Rk.CurrentSpeed＝speed。

3 应用实例

利用本文算法，针对不同生成元和障碍物（图3）可生成不同类型Voronoi图：点Voronoi图及加权图、线Voronoi图及加权图、面Voronoi图及加权图和一般图形Voronoi图及加权图等，同时以上情况还可分为顾及障碍物及未顾及障碍物两种情况。下面给出利用本算法得到的3个实例：1）一般图形Voronoi图（图4）；2）一般图形加权 Voronoi图（图5）；3）顾及障碍物的一般图形加权Voronoi图（图6）。图4、图5的生成元位置、形状一致，由于其权重不同，造成Voronoi图形状的差异。

图3 生成元和障碍物Fig.3 Generators and obstacles

图4 一般图形Voronoi图Fig.4 Voronoi diagram for general figures

图6 一般图形障碍加权Voronoi图Fig.6 Weighted Voronoi diagram with obstacles for general figures

4 结论

本文借鉴了一般图形Voronoi图、加权图及障碍物Voronoi图等研究，利用C＃和ArcEngine，以栅格结晶方式生成了顾及障碍物的一般图形Voronoi图及其加权图，取得较好的实验效果。相比以往研究，该算法有如下优点：1）与文献［1］、［16］等矢量实现方式相比，该算法中不需要考虑生成元的形状，点、线、面均可作为生成元，避免了矢量方法中计算Voronoi边界形状的大量计算。同时，考虑了线状、面状障碍物的情况，扩展了算法的应用范围。2）与文献［12－15］、［17］等栅格实现方式相比，该算法利用GIS开发组件编程实现，可移植性强，功能灵活，如可选择不同的结晶方式（棋盘距离、城区距离和欧式距离等）、不同的生成元输出方式（点生成元输出、线生成元输出、面生成元输出或三者的任意组合输出）、不同的文件输出格式（灰度图像、RGB图像、GIS矢量图）及是否加权、是否考虑障碍物等；在输出GIS矢量文件时，可选择是否包含生成元标识、颜色、权重等属性信息。该算法为研究和发展GIS空间数据结构和模型提供了重要方法，扩展了Voronoi图在地学领域的应用。

［1］ 范熙伟.加权Voronoi图矢量生成算法研究及其实现［D］.西安：西北大学，2011.

［2］ GOLD C M.The meaning of neighbor［J］.Lecture Notes in Computing Science，1992（39）：220－235.

［3］ 陈军.Voronoi动态空间数据模型［M］.北京：测绘出版社，2000.

［4］ 张有会，李秀丽，杨立平，等.Voronoi图画法的改进与实现［J］.计算机科学，1999，26（11）：86－87.

［5］ LOWELL K，GOLD C.Using a fuzzy surface＿based cartographic representation to decrease digitizing efforts for natural phenomena［J］.Cartography and GIS，1995，22（3）：222－231.

［6］ 赵仁亮.基于Voronoi图的空间关系计算研究［D］.长沙：中南大学，2002.

［7］ 王新生，刘纪远，庄大方，等.Voronoi图用于确定城市经济影响区域的空间组织［J］.华中师范大学学报（自然科学版），2003，37（2）：256－260.

［8］ SHARIFZADEH M，SHAHABI C.Processing optimal sequenced route queries using Voronoi diagrams［J］.GeoInformatica，2008，12（4）：411－433.

［9］ 覃瑜，师学义.利用Voronoi图的城乡居民点布局优化研究［J］.测绘科学，2012，37（1）：136－138.

［10］ 张伟松.基于Voronoi图的数字电视地面广播站选址分析［D］.北京：中国测绘科学研究院，2011.

［11］ 张有会，浅野哲夫，小保方幸次，等.关于一般图形Voronoi图的近似构造法的研究［J］.数值计算与计算机应用，2002（3）：216－225.

［12］ 赵晔，张有会，赵志辉，等.关于一般图形Voronoi图的离散构造法的研究［J］.计算机应用与软件，2004，21（6）：76－78.

［13］ 曹清洁.障碍Voronoi图的结晶生成［D］.石家庄：河北师范大学，2004.

［14］ 安志宏.线段障碍城市Voronoi图的结晶生成［D］.石家庄：河北师范大学，2007.

［15］ 董雪.障碍Voronoi图性质及其应用研究［D］.哈尔滨：哈尔滨理工大学，2011.

［16］ GONG Y X，LI G C，TIAN Y，et al.A vector－based algorithm to generate and update multiplicatively weighted Voronoi diagrams for points，polylines，and polygons［J］.Computer ＆Geoscience，2012，34：118－125.

［17］ DONG P L.Generating and updating multiplicatively weighted Voronoi diagrams for point，line and polygon features in GIS［J］.Computer ＆ Geoscience，2008，34：411－421.

［18］ BERTIN E，CHASSERY J M.3－D Voronoi diagram：Application to segmentation［A］.International Symposium on Voronoi Diagrams in Science and Engineering［C］.1992.197－200.

［19］ 章毓晋.图像处理和分析基础［M］.北京：高等教育出版社，2002.