供水管网模型水质不确定性研究*

龙天渝， 王军慧

(重庆大学 城市建设与环境工程学院,重庆400045)

供水管网的水力模型在工程应用中比较多，水质模型由于其复杂性，工程应用还比较少。导致水质模型的不确定性的因素众多，不仅包括水力输入参数：节点流量Q和管段水损系数C；还包括水质输入参数：主体水反应系数kb和管壁反应系数kw。对供水管网模型的不确定性研究，以水力的不确定性的研究见多，而水质不确定研究的研究较少。Kapelan等[1]在仅考虑节点流量不确定性的条件下，提出了一个随机优化设计模型，并用遗传算法进行了求解。刘孟军[2]用一阶泰勒展开式导出的节点压力和管段流量对节点流量的近似偏导矩

金溪[3]用线性化供水管网概率水力模型，研究了节点流量的随机性对管网水力特性的影响，研究发现当节点流量的变异系数较大时，进行线性近似的随机性分析会导致较大的误差。Barkdoll[4]在一个较小的供水管网之上，分析稳态流和非稳态流条件下了节点流量对于水压和水质的影响，这里的节点流量是基本用水量，给定节点流量的分布特征是高斯分布和均匀分布。

分析以上研究以及相关研究可以发现，目前有关供水管网模型的不确定性的研究，主要针对节点流量的随机性或输入数据的误差引起的管网系统模型参数的不确定性，而针对供水管网模型主要校核参数的不确定性对于水质的影响的研究极少。为此，在假定Q(基本用水量)、C、kb和kw的随机性都服从正态分布的前提下，使用蒙特卡罗随机抽样法，对所获的输入参数的抽样值，应用动态水质模型计算供水管网的节点水质，研究了基本用水量、水损系数、主体水反应系数和管壁反应系数单独作用及共同作用下对供水管网节点水质不确定性的影响，并给出了应用实例。

1 研究方法

因为不确定性本身是一个概率的现象，输入参数是随机取值的，在供水管网的不确定性的分析中应采用概率的方法。蒙特卡罗法(MCS)作为一种随机抽样算法，在供水管网模型的不确定性分析中得到了广泛的应用，并且认为以MCS计算得到的模型输出量不确定性是正确的标准，其他方法在不确定性研究中应用时应先与MCS计算的结果进行比较以确定方法是否可行。MCS是一种用数值模拟来解决与随机变量有关的实际工程问题的方法，其基本思路是，对一个具体的问题，首先建立描述该问题的概率分布模型，然后根据该概率模型进行随机抽样生成一组随机数，以随机数作为输入值计算问题的目标解，重复抽样计算过程得到目标解的统计规律，并以此作为问题的解[5]。

2 案例分析

这里采用EPANET软件安装目录下提供的案例管网Net2，Net2管网的拓扑结构如图2所示。Net2管网中包含一个水源节点1和一个水塔，水源节点1的供水是断续的，消毒剂都是从水源节点1进入管网中。模型输入参数：水力输入参数节点流量(包括节点基本用水量和用水模式)和水损系数不做改变。水质输入参数认为所有管道的主体水反应系数相同，kb= -0.8 d-1；供水管网的管壁余氯衰减系数分成两类，管径DN300的管壁系数为kw1= -0.648 d-1，管径DN200的管壁系数为kw2= -0.792 d-1(供水管网只有这两种管径的管段)，余氯反应为一级反应。对Net2管网执行延时水力水质分析的时间为55 h，水质时间步长5 min，报告水质时间步长1 h，钟表计时开始时间12 am。

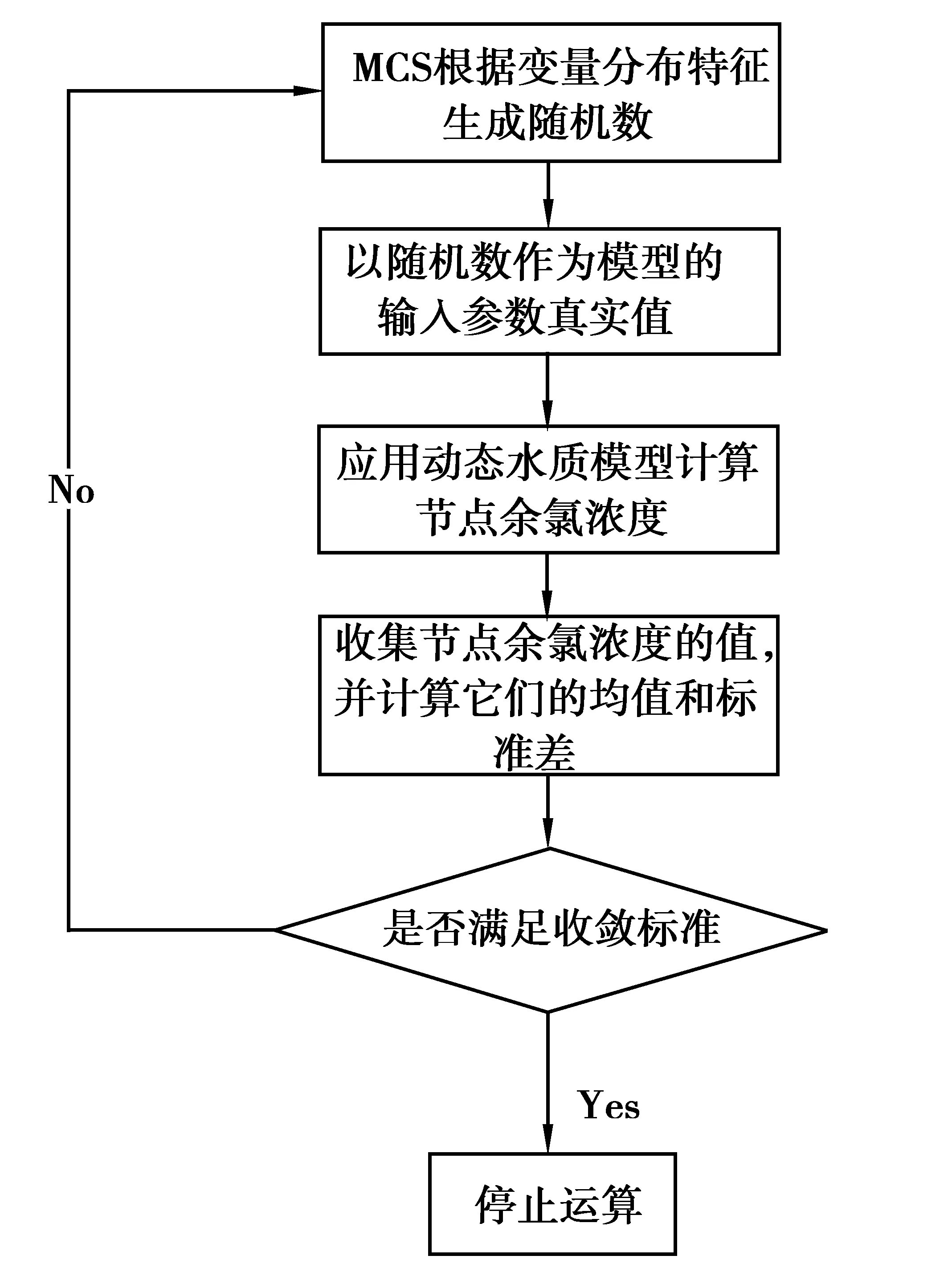
图1 算法流程图

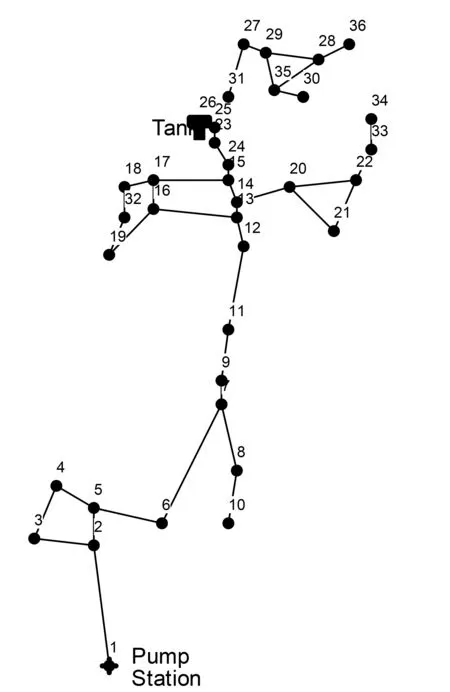
图2 Net2管网拓扑结构

为了研究输入参数对于动态水质的不确定性的影响，这里水源节点1的余氯浓度随模拟时间是不断变化的，水源节点1的源头水质为1.0 mg/L，水质变化的时间模式如图3。Net2管网用水节点的初始余氯浓度都设为0.3 mg/L。水源节点的余氯浓度随时间不断变化，且水源节点的供水是断续的，显然模拟时段内各节点余氯浓度也是随时间不断变化的。

认为Net2所有的输入参数都是服从正太分布的，量化输入参数的不确定性，输入参数的均值为模型中的值，取水损系数的变异系数为0.05，节点基本用水量的变异系数为0.1，参考Pasha[7]所有反应系数的变异系数取0.1。对Net2进行抽样模拟中，每次利用MCS生成的随机数个数为节点数、管段数、主体水反应系数(等于管段数)和管壁反应系数(等于管段数)之和。为了保证余氯浓度值统计量的充分收敛，在每次不确定性分析中都进行了3 000次的抽样计算。对Net2的余氯模型进行水质不确定性分析，通过模拟计算可以得到整个时段内节点余氯浓度的分布特征。

图4给出了在所有输入参数的共同影响下节点7在40时余氯浓度的标准差和MCS抽样计算次数的关系。节点7余氯浓度的标准差在0.003左右，节点余氯浓度的不确定度很小，这也说明了动态水质模型节点水质的鲁棒性。从节点余氯浓度的统计量和抽样次数的关系可知，即便在对这么的变量的抽样模拟时，在约1 000次的模拟计算时余氯浓度的统计值已经开始收敛。同时由于MCS在量化不确定性因素的方法简单，因此在评价诸多因素对供水管网模型的不确定性影响时，MCS不失为一种很好的方法。

图3 水源节点1余氯时间模式

图4 40时节点7余氯浓度标准差

图5和6分别给出了节点7和33在40 h余氯浓度的箱形图，其中7是靠近供水点节点，节点33是末端节点。从节点余氯浓度的箱形图中可以看出，所有不确定输入参数共同作用下，节点余氯的不确定性程度最大。单个不确定参数对节点7余氯浓度的影响程度从大到小依次是：kw、kb、Q和C，单个不确定参数对节点33余氯浓度的影响程度从大到小依次是：kb、kw、Q和C。总体来说余氯反应系数造成的不确定性程度最大，因此在水质模型校核中对主体水反应系数和管壁反应系数进行校核，是建立准确的水质模型的关键所在。比较水力模型输入参数基本用水量和水损系数对余氯浓度的不确定性影响程度，都有基本用水量的影响程度要大于水损系数，这一点和节点流量和水损系数对于节点压力的不确定影响程度的大小关系是一样的[8]。

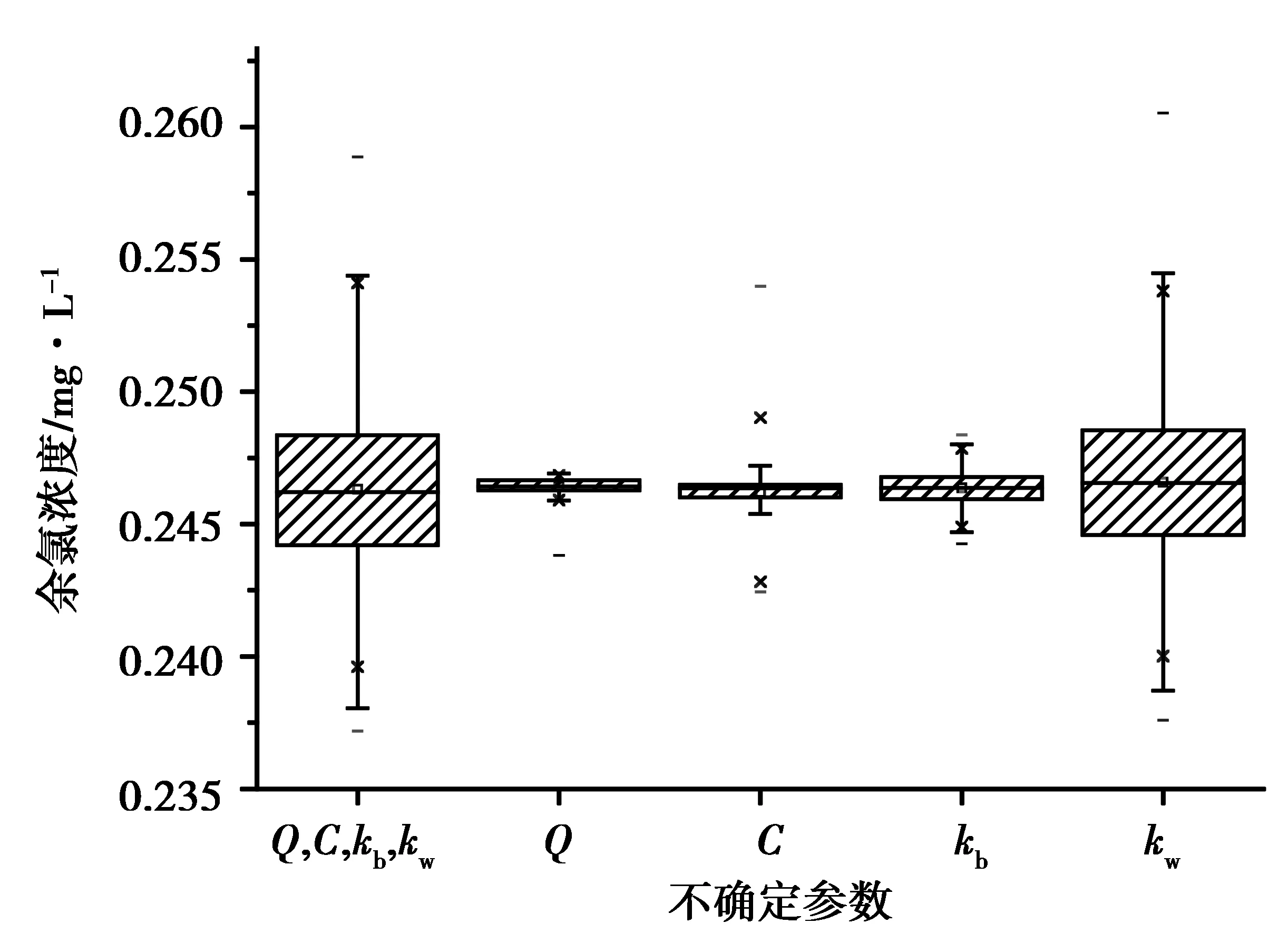
图5 节点7余氯浓度箱形图

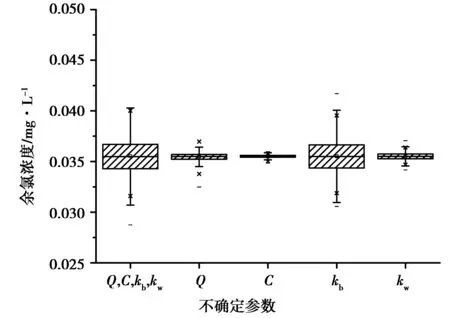
图6 节点33余氯浓度箱形图

图7和图8分别给出了在所有不确定输入参数的作用下，节点7和节点33在整个模拟时段上余氯浓度的误差图。节点7的余氯浓度曲线，有4个波谷。这4个出现的时间对应着节点1不供水的4个时间段，这时候节点7的用水是由水塔提供，节点7使用由水塔流过来的水，其水质要比由水源直接流过来要差，这是因为水在水塔中停留余氯浓度在不断衰减。同时也可以看出，在由水源节点供水向水塔供水转变时节点7余氯浓度的标准差相对较大，节点7余氯浓度标准差的最大值出现在47时的0.013 9 mg/L。

节点33的余氯浓度曲线和节点7的余氯曲线形式完全不同，从模拟时间开始节点33的余氯浓度一直在下降，这是因为节点33靠近管网末端，其水龄比较大，从起始开始由水源节点1所供给的水流到节点33需要21.89 h(节点水龄值)。那么在这个时间之间，节点33的余氯浓度只与管网中初始浓度0.3 mg/L有关，而和水源节点1的余氯浓度无关，所以曲线也一直在下降。在水源节点1流至节点33之后的3个不供水的时间段，节点33的余氯浓度曲线有上升的趋势，其中在最后一个上升趋势很明显。这个原因和节点7余氯浓度处于波谷的原因是一样的，都是因为给节点的水质供给是由一个水源切换到另外一个水源。同样的对于末端节点33而言有，由水源节点供水向水塔供水转变时节点33余氯浓度的标准差相对较大，节点33余氯浓度标准差的最大值出现在47时的0.016 2 mg/L。

图7 节点7余氯浓度误差

图8 节点33余氯浓度误差

比较节点7和节点33对应时刻节点余氯浓度的标准差，大部分时刻节点33余氯浓度标准差都是要大于节点7，这可能与节点在管网中的相对位置有关，节点33位于管网末端，其节点水龄比较大，同一时刻流至末端节点的水受到的不确定因素的影响比前端水龄较小的节点要多，所以其受不确定性参数的影响较大。

和水力模型的不确定分析类似，水质模型的不确定分析可以用水质的不确定区间作为水质模型计算的值，这样更能准确的把握供水管网中的水质情况。通过节点水质的分布情况，对供水管网的水质可靠度进行评估。在实际的供水管网模型的应用中，如果发现在出厂水水质满足标准的情况下，监测节点的余氯浓度值长时间小于水力模型计算的节点水质不确定区间下限值，则供水管网中可能发生了如下情况：(1) 监测设备故障，导致所监测的余氯值与实际情况不符；(2) 供水管网发生污染事故，监测节点的余氯浓度值无法保障供水安全。建议建模工作者可以将监测节点水质不确定区间的下限值作为管网事故预警的标准，当监测节点的监测余氯浓度值频繁小于标准值时发出预警信号，提醒相关工作人员对供水管网中存在的问题进行核实和处理。同时水质不确定区间可以为水厂消毒剂的投加剂量提供参考等。

3 结论

(1) 由输入参数所导致动态水质模型节点余氯浓度的不确定性是很小的，动态水质模型具有鲁棒性。

(2) 在水力和水质不确定输入参数的共同作用下，节点余氯浓度的不确定性最大；余氯反应系数是对余氯浓度影响程度最大的输入参数，在水质模型校核时应针对主体水反应系数和管壁反应系数进行校核；水力输入参数节点基本用水对水质的不确定性影响的程度要高于水损系数。

(3) 同一时刻一般有末端节点余氯浓度的不确定性要大于前端节点，且当节点用水由一水源切换到另外一水源时，节点余氯浓度的不确定性程度最大。

参考文献：

[1]KAPELAN Z, SAVIC D, WALTERS G A. Robust least cost design of water distribution systems using Gas[J]. In Proceedings of the computer control for water industry CCWI, 2003(2):101-105

[2]刘孟军,邹平华,何钟怡. 供水管网中节点流量随机性的影响分析[J].给水排水，2007,33:350-354

[3]金溪. 供水管网概率水力模型线性化求解方法[J].河海大学学报，2011,39(4)：458-463

[4]BARKDOLL B D, DIDGAM H. Effect of user demand on water quality and hydraulics of distribution systems[J].Proc World Water & Environmental Resources Congress， 2003(6)：107-109

[5]王中宇,刘智敏，夏新涛. 测量误差与不确定度评定[M]. 北京：科学出版社,2008

[6]谢善斌, 金波, 刘遂庆. 基于不确定度量的给水管网用户的用水模式分析[J].中国给水排水,2011,27(7): 59-62

[7]PASHA M F K. Uncertainty Analysis and Calibration of Water Distribution Quality Models[D]. Tucson Arizona:Universityof Arizona,2006

[8]PASHA M F, LANSEY K. Analysis of uncertainty on waterdistribution hydraulics and water quality Proc[J]. World Water Congress, 2005(6)：207-209