多子样服从同一线性模型的检验*

李光辉， 张 洪， 叶绪国

(1. 凯里学院 数学科学学院，贵州 凯里 556011；2. 东南大学 数学系，南京 210096)

1 问题的提出

含有p-1个自变量的理论线性回归模型一般形式为

y=Xβ+e，E(e)=0， Cov(e)=σ2I

(1)

其中y为n×1的观测向量，X为n×p的已知设计阵，且rank(X)=p，e为n×1的随机误差向量，模型中n次观测到的数据记为Ai=(yi,xi1,…,xi,p-1)，i=1,2,…,n，并记W={A1,A2,…,An}为n组观测值所组成的样本空间，Ai为其中的样本点.对于模型(1)，通过最小二乘法可获得β的LSE，建立经验回归方程为

(2)

记Lj={Aj1,Aj2,…,Ajnj}是由W中的nj个样本点所组成的子样，即Lj⊆W,j1,j2,…,jnj为自然数1，2，…，n中的nj个数.易知，W中共包含2n个子样.

现考虑以下情形：若W中存在m个子样L1,L2,…,Lm，且满足p+1≤nj≤n-1,j=1,2,…,m,即在这m个子样下建立的经验回归方程和参数β的LSE为

(3)

这k个经验回归方程与总数据下的回归方程(2)具有较大的差别，且拟合效果明显优于式(2).以一元线性回归为例，图1给出了两组数据的散点图及拟合直线.

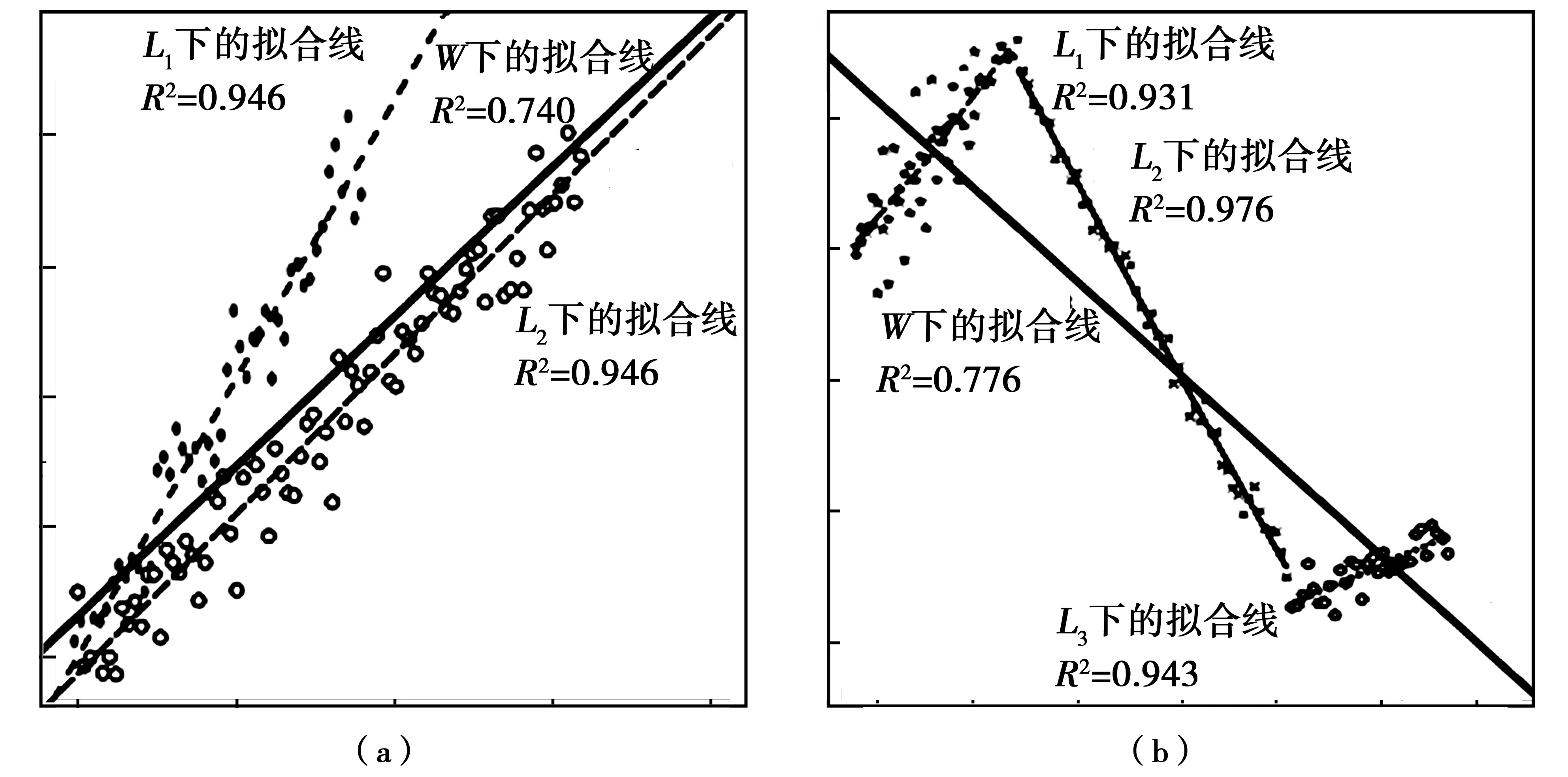
图1 子样下的经验回归方程与总体回归方程的差别示意图

如图1示，两组数据下所建立的回归方程都通过了R检验，在W下的R2都大于0.7，说明两组数据的线性关系都显著，但图1(a)中数据取得两组子样下所建立的回归方程与总回归方程差别较大，但拟合效果更佳；图1(b)中的散点呈明显分段，用3段拟合所得的回归方程拟合效果明显优于总回归直线，所以，在以上两种线性关系都显著的情形下，对总回归方程的拟合效果仍然提出质疑.

同理，在多元回归模型中，即使总回归方程通过了F检验，且每个自变量系数都通过了t检验，若以均方误差来度量回归方程的拟合效果，在W中的k个子样下的回归方程与总回归方程差别较大，且具有更小的均方误差，但总回归方程的拟合效果欠佳.

所以，线性模型的同一性就是指，在总回归方程显著的条件下，对于∀Lj⊆W，在Lj下建立的子样回归方程(3)与总回归方程(2)之间不存在较大差别，拟合效果相近.线性模型的同一性检验就是对k个子样作如下检验：

H0：β(j)=β,j=1,…,m； H1：β(j)不全等于β

(4)

张双林[1，2]对多组自相关数据服从同一模型作了假设检验.此处在此基础上，利用文献[3]中的方法，提出利用自助法获得W中的k个子样，通过文献[4]中的结论，对每个子样分别建立回归方程，检验整体数据W是否服从同一线性模型，并导出了检验统计量.

2 自助样本作同一性检验的可行性

设从W中取出m个完全不同的自助样本，并保证每个自助样本下的已知设计阵X(j)都是列满秩的，记为

Lj={Aj1,Aj2,…,Ajnj}，j=1,2,…,m，p+1≤nj≤n-1

(5)

特别地，每个自助样本中取a个样本点，若a≤ni，i=1,2，…,k，则取到这些子样的概率为

若a≥ni时，i=1,2，…,k，取到这些子样的概率为

所以，不论以何种方式获得自助样本，只要W含有不满足同一性的子样越多，就会导致取到该子样的概率越大，进一步构造的检验统计量中也会含有更多与总模型相悖的信息.

3 同一性检验

设m组自助样本下的理论线性回归模型为

yij=β10+βi1xi1j+…+βi(p-1)xi(p-1)j+eij,i=1,…,m,j=1,…,nj

(5)

其中yij和eij分别表示第i组自助样本下的第j次的观测值和随机误差，βik表示第i组自助样本下的第k个未知参数，xikj表示第i个自助样本下的第k个变量的第j次观测值，k=1,2，…,p-1.将模型(5)记为矩阵形式得

y(i)=X(i)β(i)+e(i),e(i)～N(0,σ2Ini),i=1,2，…,m

(6)

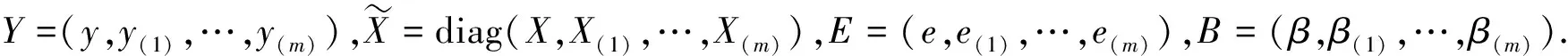
(7)

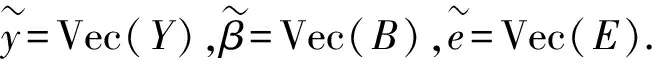
现需要检验的假设(4)可记为

(8)

下面计算模型(6)下的残差平方和SSe与约束残差平方和SSHe.

(9)

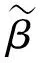
(10)

由式(9)(10)得

由于SSHe-SSe～χ2(p)，SSe～χ(N+n-(m+1)p)且两者相互独立，则可得到检验统计量为

(11)

有F～F(p,N+n-(m+1)p)，对于给定的水平α，若F>Fα(p,N+n-(m+1)p)，则拒绝原假设，认为模型不满足同一性，此时不认同模型具有良好的预测水平.

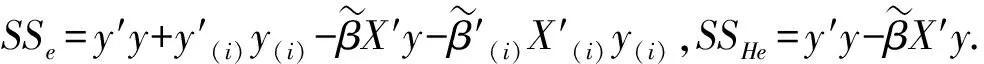
由此得到的检验统计量为

更进一步，若每个自助样本中的样本容量都为α，此时检验统计量为F～F(p,m(a-p)+n-p).

参考文献：

[1] 张双林，沙秋英.k组多元自相关数据服从同一模型的假设检验[J].应用数学学报，1995，18(4)：518-527

[2] 张双林，陈超. 线性模型的等价性检验[J].黑龙江大学学报，1997，14(1)：1-8

[3] 王松桂.线性模型引论[M]. 北京：科学出版社，2004

[4] 胡雪梅，吴代红，李楠.基于原始自助法估计异方差线性模型[J]. 重庆工商大学学报：自然科学版，2010，27(1)：15-17