基于模糊支持向量机的信用风险评估模型研究

林 于 力

(重庆大学 数学与统计学院，重庆 401331)

20世纪30年代至今，金融经济危机频频发生，信用风险评估成为金融风险管理领域的重要课题。实证研究表明：支持向量机模型(SVM)是研究信用风险评估问题的最好模型之一[1]。SVM的主要思想是最小化泛化误差的上界，在机器学习过程中，对训练样本需要解一个二次规划。当遇到一个大型的二次规划问题时，计算会很复杂。因此，解二次规划问题的算法影响着支持向量机模型的性能。另外，在实际生活中，不能完全确定每个信用申请者是属于可信客户还是违约客户。例如，一个申请者有90%可能属于可信(不违约)客户，有10%可能属于违约(不可信)客户，很难100%判定申请者是可信的还是违约的。因此，应为信用申请者设置一个模糊隶属度，对信用风险评估问题应进行模糊化处理。

针对以上问题，本文利用试验设计方法和模糊支持向量机，构造基于试验设计的模糊支持向量机模型来进行信用风险评估。在该模型中，首先采用试验设计方法为模型选择最优参数，然后利用模糊支持向量机来处理信用评估问题。此外，为了减少支持向量机求解二次规划问题的计算复杂度，利用最小二乘原理进行简化处理。最后，用来自UCI机器学习库中的德国信用数据集对提出的方法进行实证分析。

1 基于试验设计的模糊最小二乘支持向量机模型

1.1 模糊最小二乘支持向量机模型的构造

支持向量机首先通过映射函数φ(·)把输入数据映射到一个高维的特征空间中，并找到有最大分类间距的最优分离超平面。最优超平面表达如下：

y=wTφ(x)+b=0

(1)

其中，x=(x1，x2，…，xN)T，N为样本数，w为超平面的法向量，b是偏差，为一个标量。根据结构风险最小化原则，分类超平面问题可以通过如下的优化问题求解：

(2)

寻找最优超平面是一个二次规划问题，有较高的计算复杂性，因此，基于最小二乘原则进行求解。在实际的信用分类问题中，每个样本数据不能完全明确的分到一个特定的类里，引入模糊隶属度μi，模型变为

(3)

为训练数据的每个元素指定αki，相应的拉格朗日函数为

(4)

由KKT点的必要条件，代入式(4)，有：

(5)

上述等式可写为

(6)

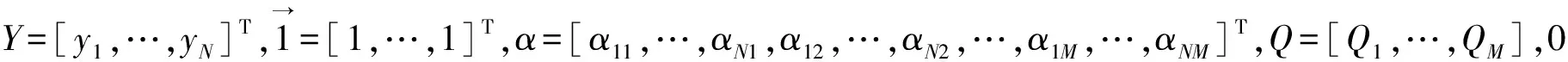
分类器为

(7)

最后，模型变为

(8)

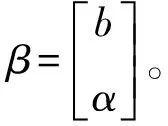
输入空间到高维特征空间的非线性映射取径向基核函数：

(9)

对于隶属度μi，选择公式：

(10)

sk是由SVM，LSSVM等信用评分方法得到的每个输入数据的初始信用评分。

1.2 分类器参数选择的方法

支持向量机的性能不仅受解优化问题的算法所影响，在机器学习的过程中参数的选择也是很重要的。试验设计法(DOE)的主要思想如下：首先，设定一个覆盖了整个搜索空间的粗糙网格；然后，迭代网格解析度和搜索边界直至满足停止准则。每次迭代后，搜索空间重新设定为以最优性能的点为中心。如果上述过程使搜索边界超过了给定的界，调整中心使整个空间包含在给定的界中。

以两个参数的设定为例。让每个参数取值[-5，5]，图1表示以1×1为精度，网格搜索法总共要评估的点是100；图2表示用DOE方法需要评估的点及其迭代，圆表示第一次迭代的点，三角形表示第二次迭代的点。

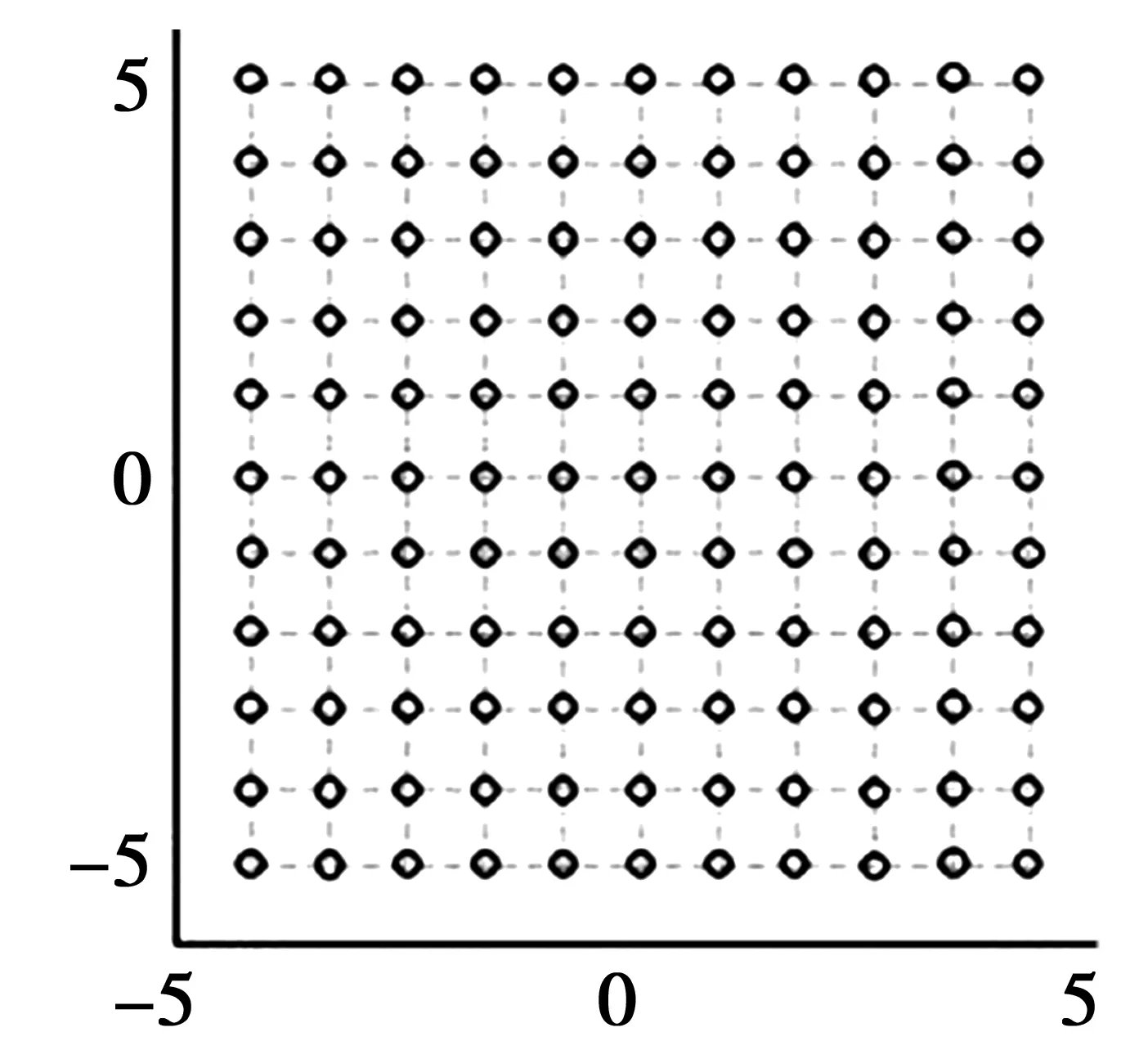
图1 网格搜索法评估的点

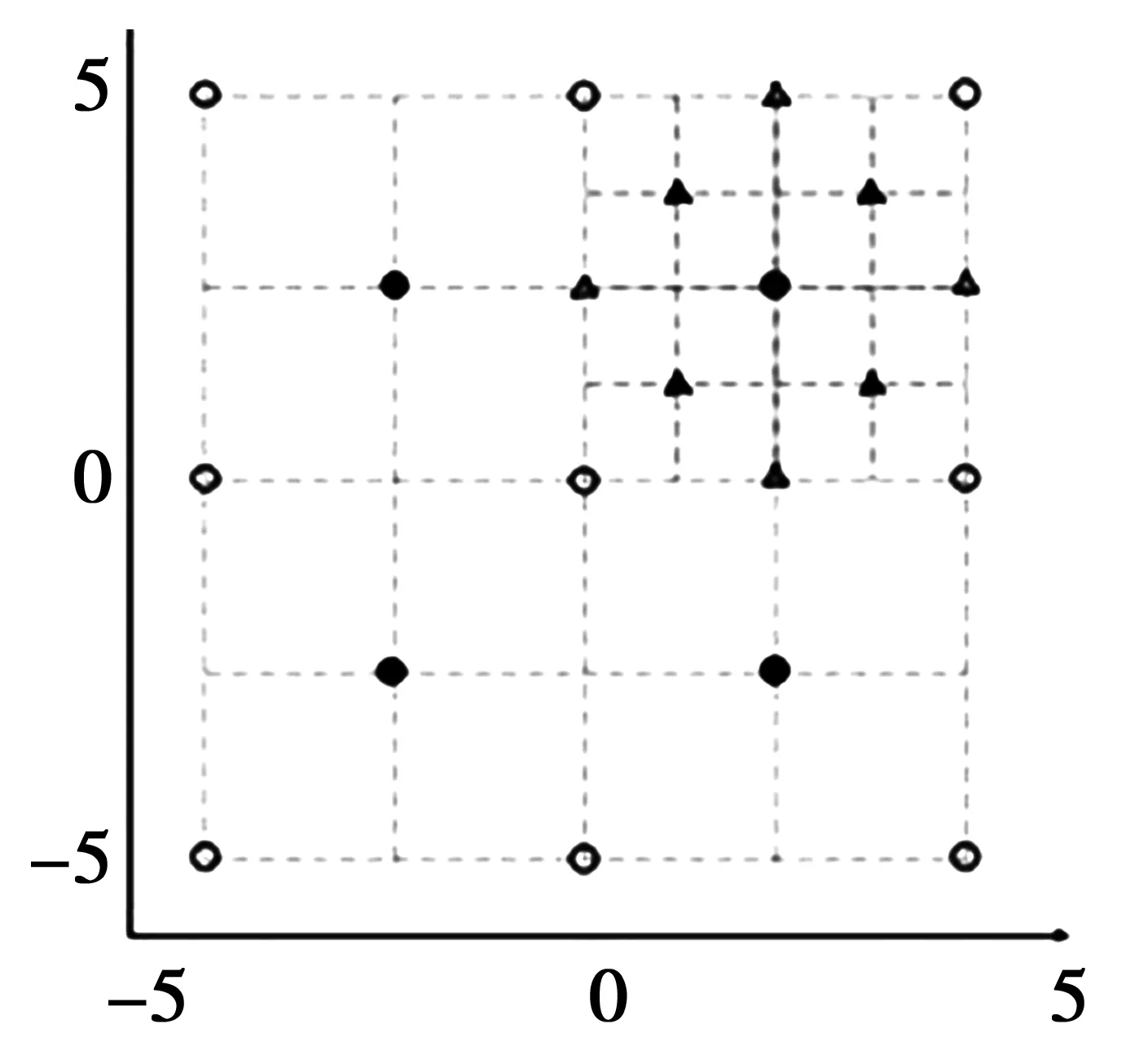
图2 DOE方法评估的点

寻找径向基核函数的最小二乘支持向量机的参数，DOE方法主要步骤如下：

(1) 设定γ和σ的初始范围为[γ_min，γ_max]，[σ_min，σ_max]，iter=1；

(2) 当iter≤MAXITER时，根据图2的模式，找到空间中的13个点，以(γ_min，σ_min)为左底角，(γ_max，σ_max)为右上角，由[(γ_min，σ_min)，(γ_max，σ_max)]表示，设γ_Space=γ_max-γ_min，σ_Space=σ_max-σ_min。

对这13个没有进行评估的点，进行评估：以点的坐标作为参数，用训练和测试样本运行径向基核的最小二乘支持向量机M次，这M次检测的平均分类准确度就是这个点的性能指数。

选择具有最优性能的点P0(γ0，σ0)作为中心，设定一个新的搜索空间范围：γ_Space=γ_Space/2，σ_Space=σ_Space/2。如果以(γ0，σ0)为中心，γ_Space、σ_Space为宽和高的长方形超过了最初的范围，调整中心点直到新的搜索空间包含在[(γ_min，σ_min)，(γ_max，σ_max)]内。

设定新的搜索空间：γ_min=γ0-γ_Space/2，γ_max=γ0+γ_Space/2，σ_min=σ0-σ_Space/2，σ_max=σ0+σ_Space/2，iter=iter+1。

(3) 返回有最优性能的点，选择最优参数构造模糊最小二乘支持向量机模型进行分类。

1.3 基于试验设计的模糊最小二乘支持向量机模型的信用风险评估算法

使用Matlab，采用径向基核函数，用DOE法找到最优参数σ2，γ，使用σ2和γ来训练和检验输入数据。算法步骤如下：把数据转为Matlab能识别的格式；初始化参数σ2和γ，然后使用DOE方法进行参数选择；使用标准LSSVM模型计算得分sk，计算μk，解决数学规划，得到拉格朗日乘数α和数量b；构造分类函数，对检验数据分类；计算三种类型的精度(总精度，一类精度，二类精度)。其中：

如果对得到的精度不满意，改变σ2和γ的初始值。

2 实证分析

为了检验所提出方法进行信用风险评估的效果，选择来自UCI机器学习库中的德国信用数据集(http：//archive.ics.uci.edu/ml/)进行实证分析。其中，德国信用数据集包括1 000位申请者(700位可信客户，300位违约客户，分别对应标签为1和-1)，每位客户有24个属性；数据集中可信客户和违约客户是不平衡的，和现实情况相符。

使用径向基核函数，模型中只有σ2和γ两个待定参数。采取DOE方法，初始范围设为γ[2-5，29]，σ[2-9，25]，maxiter=6，检验的次数为10次；选择601个数据作为训练样本，剩下的399个数据作为测试样本对模型的精度进行检验，并与线性判别分析法(LDA)、最小二乘支持向量机(LSSVM)、支持向量机(SVM)、径向基网络(RBF)和k邻近等常用的信用风险评估模型的精度进行比较，结果如表1所示。

由表1可知，模糊最小二乘支持向量机模型的总精度和第二类精度都高于其他模型。第一类精度仅次于径向基网络模型，也远高于其他模型精度的平均值。这说明了所提出的模糊最小二乘支持向量机模型对信用风险评估有很好的效果。

得到这个较好的结果的原因之一是DOE方法得到了模型的最优参数，而DOE更是一种能够有效减少计算复杂度的参数选择算法。对上述德国信用数据集选用最小二乘支持向量机模型进行信用风险评估，选择100个数据作为训练样本，20个数据作为测试样本，并用DOE方法和网格搜索法(GS)分别进行参数选择，得到的结果和所花费的时间如表2所示。由表2可知，用DOE方法做参数选择所得到的第二类精度和总精度都高于用网格搜索法做参数选择得到的精度，第一类精度略低，但也处于一个较高的水平。但DOE方法所耗时间为4.7 s，远低于网格搜索法所需要的时间，因此用DOE方法进行参数选择是有价值的。

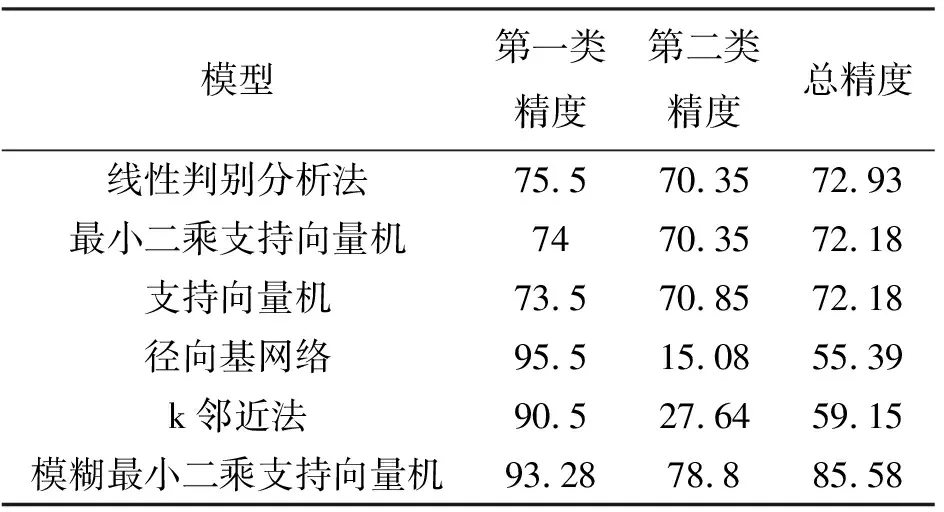
表1 不同信用风险评估模型的精度比较 %

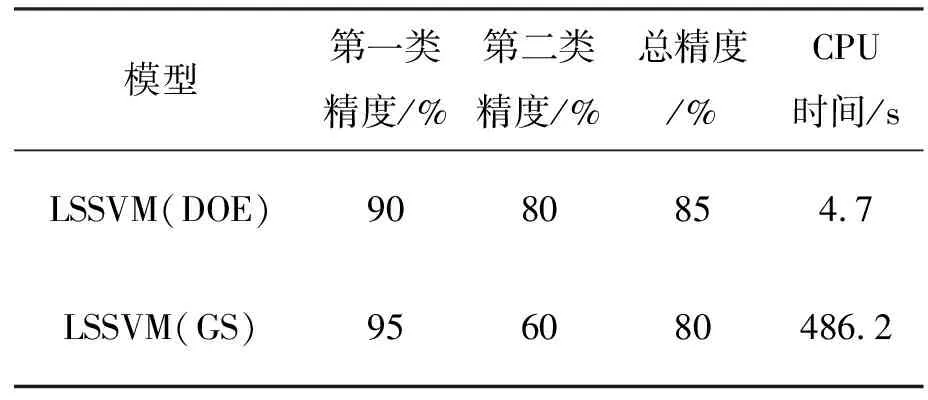
表2 LSSVM两种参数选择方法的结果比较

3 结 论

作为有效防范信用风险的主要手段，信用风险评估在信用管理中发挥着重要的作用，本文用基于试验设计的模糊最小二乘支持向量机模型对信用数据进行信用风险评估。在此模型中，利用DOE方法进行参数选择，再利用模糊最小二乘支持向量机模型对数据进行分类，得到不同客户的信用评估情况。为了检验该方法，使用UCI数据库中的德国信用数据集信用数据集来进行实证分析，研究结果表明：基于试验设计的模糊最小二乘支持向量机模型能取得较好的分类结果，且运行速度较快，可为信用决策者提供重要的决策参考依据，具有较强的实用性。此外，基于试验设计的模糊最小二乘支持向量机模型也可应用于其他二分类问题，因而此模型具有较强的适用性。

参考文献：

[1] LEAN Y，WANG S Y，LAI K. Credit risk evaluation using a C-variable least squares support vector classification model[J].Communications in Computer and Information Science，2009(35)：573-579

[2] 余乐安，汪寿阳.基于核主元分析的带可变惩罚因子最小二乘模糊支持向量机模型及其在信用分类中的应用[J].系统科学与数学，2009(10)：1311-1326

[3] YU L，YAO X，WANG S Y，et al. Credit risk evaluation using a weighted least squares SVM classifier with design of experiment for parameter selection [J]. Expert Systems with Applications，2011，38：15392-15399

[4] LIU J L，MAO J Q，CHEN L. An Ensemble of Fuzzy Sets and Least Squares Support Vector Machines Approach to Consumer Credit Risk Assessment[J]. Fifth International Conference on Business Intelligence，2012(5)：10-12

[5] 余晨曦，梁潇.基于支持向量机的商业银行信用风险度量模型[J].计算机与数字工程，2008(11)：10-14

[6] TWALA B. Multiple classier application to credit risk assessment[J]. Expert Systems with Applications，2010(37)：3326-3336

[7] 张冰，孔锐.一种支持向量机的组合核函数[J].计算机应用，2007，27(1)：44-46

[8] 奉国和.SVM分类核函数及参数选择比较[J].计算机工程与应用，2011，47(3)：123-128