重庆市CPI与PPI关系分析

2014-08-08郑孟雪

重庆工商大学学报（自然科学版） 2014年5期

郑孟雪

(重庆师范大学数学学院，重庆 400047)

消费者价格指数和工业品出厂价格指数是我国价格体系中最重要的两种价格指数，分别反映消费领域居民消费价格和生产领域工业企业产品出厂价格的变动情况。物价指数是通货膨胀的晴雨表，工业品出厂价格指数和消费者价格指数变动是否一致是反映经济结构是否合理的标志之一。但两种价格指数之间究竟是存在怎样的关系仍有待研究。现拟用回归分析的方法，运用了Matlab软件编程、Excel数据分析等手段得到指数之间存在密切的线性相关关系，通过建立一元线性回归模型和一元线性回归方程，分析了CPI与PPI的线性相关关系，并且对所建立的模型进行了验证，得到了拟合度较高的一元线性回归模型。

1 CPI和PPI的经济内涵

消费者价格指数(Consumer Price Index，简称CPI)，即商品进入消费领域时的价格或消费者购买价格，是反映居民购买并用于消费的一组代表性商品和服务项目价格水平的变化趋势和变动幅度的统计指标。生产者价格指数 PPI 是衡量工业企业产品出厂价格变动趋势和变动程度的指数，是反映某一时期生产领域价格变动情况的重要经济指标，也是制定有关经济政策和国民经济核算的重要依据。两种价格指数在计算过程和用途上区别很大，但是现实的经济生活中，两种价格指数之间彼此又存在着非常密切的关系。根据流通经济学理论，从供给角度，PPI很大程度上决定着CPI；从需求角度，CPI反过来也影响PPI。

2 CPI与PPI关系分析

2.1 CPI和PPI关系的描述性分析和相关分析

摘录了《重庆市统计年鉴》1994-2010年的相关统计数据，用作对CPI和PPI的相关关系初步分析，如表1。

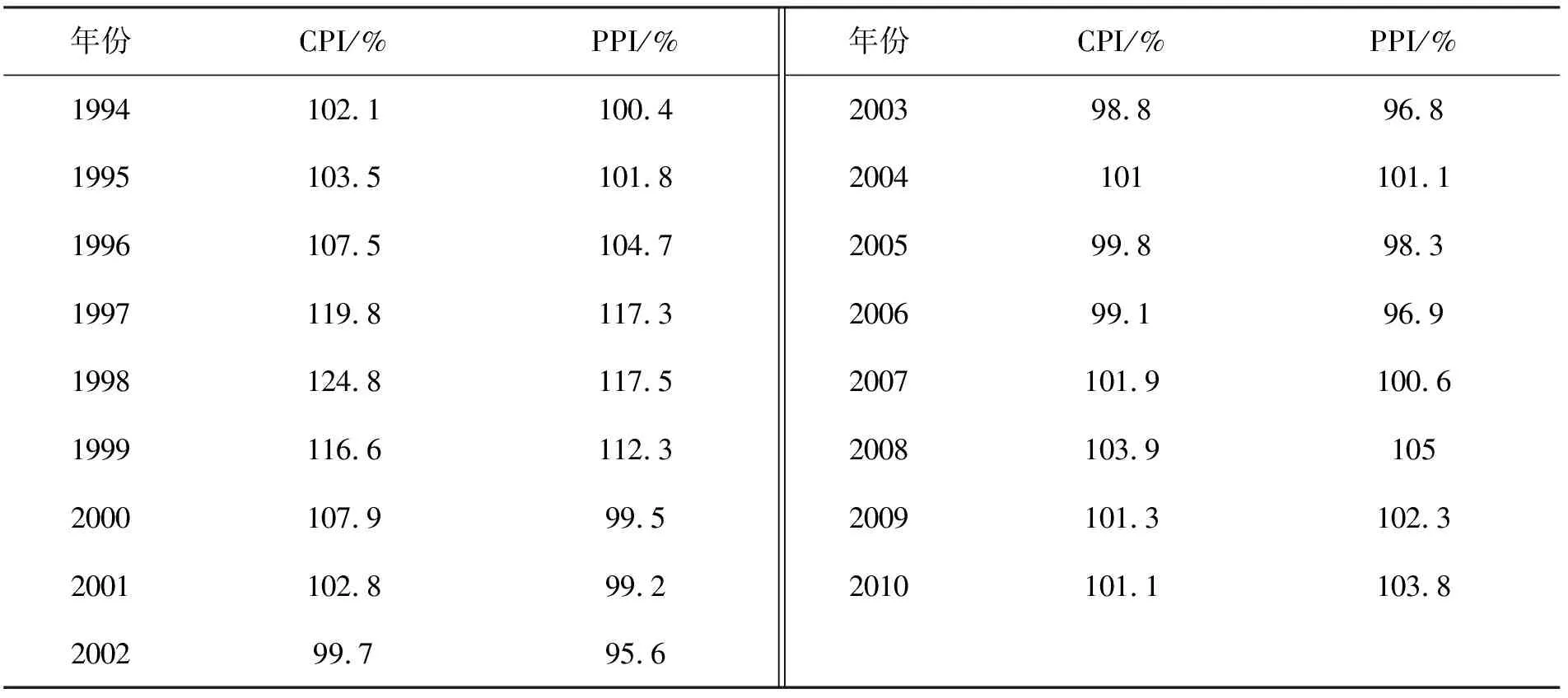
表1 重庆市PPI与CPI指数①

① 资料来源：《重庆市统计年鉴1994》至《重庆市统计年鉴2010》

先以时间的角度来分析其二者之间的关系，为了能更加直观的观测PPI与CPI之间所呈现的关系，用Excel软件作出从1994至2010这17年的CPI和PPI指数的时间序列，如图1所示。

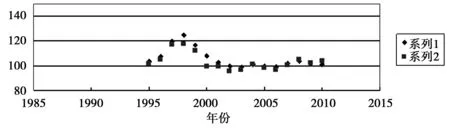
图1 重庆市PPI和CPI指数时间序列

从图1的数据可以看出CPI于PPI的变动趋势具有高度一致性，大致能够呈现同增同减的高度相关性，从上图中可以看出在2002年以后，CPI与PPI几乎重合，表明它们具有高度相关性，但是在有的时间段内两条曲线中间有较大空隙，变动方向完全相同，并且CPI在上方，表明CPI变动引起PPI变化，但是PPI还受到其他因素的影响，所以它们没有重合。能够看出二者存在一定的同增同减关系，可能有线性函数关系，但是若具体来讨论两者之间的关系，需作出仅含两者的图形，现用Excel软件作出两者指数的散点图，如图2所示。

图2 重庆市CPI与PPI指数散点

从图2可以看出CPI和PPI大致存在线性关系，但曲线有慢慢趋于平稳的趋势，故猜测还可能具有抛物线与对数的函数关系。猜测其可能具有线性关系，具体的函数关系仍需进一步分析。

对PPI和CPI进行相关性计算：

由表1的数据，运用Matlab软件进行相关系数分析可得到CPI和PPI皮尔逊相关系数r=0.934。

接下来对皮尔逊相关系数进行检验：样本相关系数是否能够真实的代表总体变量之间的相互关系，需要通过统计检验来决定。

数理统计学证明，t统计量可以用来检验相关系数的显著性。

H0：r=0 ；H1：r≠0

根据表1的数据，计算t值得：

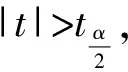
1994-2010年，PPI和CPI之间的相关系数为r=0.934，这说明PPI与CPI存在着高度的线性相关关系。

2.2 CPI和PPI关系的线性回归分析

2.2.1 一元线性回归模型

记构成CPI因素中的PPI为自变量x，CPI为因变量y，表1中的样本数据为(xi，yi)(i=1，2，…，67)，绘制散点图(图2)，可以直观地看出y与x大致呈线性关系，经计算相关系数r=0.934，说明二者具有高度的线性相关关系。当两个变量之间有着密切的关系，但密切的程度不能由一个变量惟一确定另一个变量，即它们之间的关系是一种非确定性的关系，那么就可以使用一元线性回归模型进行分析。[1]

采用一元线性回归模型：

y=β0+β1x+ε，ε～N(0，σ2)

(1)

进一步有y～N(β0+β1x，σ2)，它表示随机变量y也遵从正态分布，式(1)称为一元线性回归模型。

用Matlab统计工具箱[5]的lsline函数能够会指出数组x和y按照最小二乘法得到的拟合直线(图3)。

计算结果可以整理成表2：

表2 PPI与CPI的回归分析

由计算结果可以看出虽然F统计量并非太大，但是p值为0，且p<α，可以说明模型是有效的。并且决定系数R2接近1，说明回归模型的拟合精确程度比较高，回归直线与样本观察值拟合得比较好。

在MATLAB统计工具箱中regress函数进行线性回归分析的计算之后，用函数rcoplot绘制残差图形(图4)。

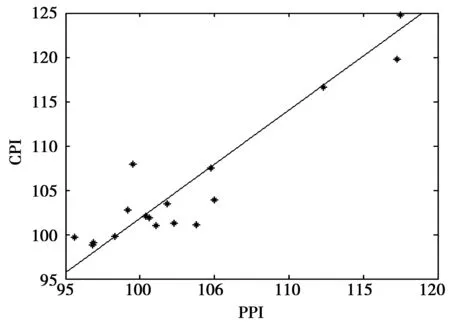
图3 CPI和PPI的线性回归模型拟合直线

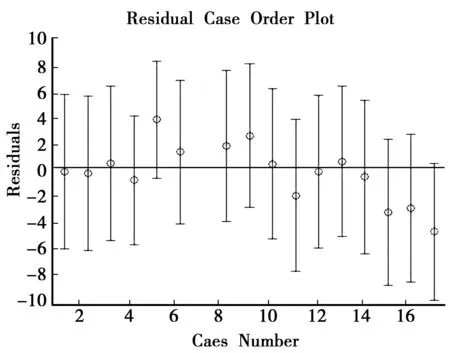
图4 所建线性模型的残差

从图4看出残差数据都在零点附近(残差应服从均值为0的正态分布)，说明ε具有随机性和正态性；第7个数据的误差均值置信区间不含零点，但是置信区间偏离零点的程度不严重，不必剔除。此一元线性回归模型的自变量和因变量有显著的线性相关关系，回归直线对原观测值的拟合情况良好，所以回归模型已具备较好的拟合度。

2.2.2 一元线性回归方程

由表2，有：

β0=-6.893 6 ；β1=1.088 8

则可以得出线性回归方程为：CPI= -6.893 6+1.088 8 PPI。

由上面残差分析可以得出ε是随机变量，通常就用E(y)作为y的估计，

故得：

(2)

(3)

式(3)为y关于x的一元线性经验回归方程。

2.2.3 回归效果显著检验

① 回归系数的显著性检验。

H0：β1=0 ；H1：β1≠0

② 回归方程的显著性检验。

在一元线性回归时回归方程的显著性检验和回归系数的显著性检验是等价的，所以这里不再进行检验，说明此线性回归方程具有实用意义。

3 结语

选取了近17年的数据来讨论PPI和CPI之间的关系，经过仔细观察、认真分析，采用数据统计中的回归分析方法进行考虑，通过建立数学模型，最终得到了两者拟合度较高的一元线性回归模型。

从国家经济发展经验表明，在一定时期内，国家经济增长与其CPI和PPI总水平之间存在密切关系。主要体现在：经济繁荣时期，市场投资需求旺盛从而带动投资成本上扬(生产价格指数上升)，部分投资通过劳动报酬方式转化进入消费需求，进而促使消费品价格指数上升；经济萧条时期，由于投资消费需求下降，消费品价格指数回落。

CPI和PPI对国民经济具有一定的反映能力，根据价格传导规律，PPI 对CPI有一定的影响。PPI 反映生产环节价格水平，CPI反映消费环节的价格水平。整体价格水平的波动一般首先出现在生产领域，然后通过产业链向下游产业扩散，最后波及消费品。为防止短期内CPI指数快速上涨，政府应从以下着手。

首先，加强市场价格监测分析工作，将PPI稳定在一定范围内，对加工和运输的环节加强监控力度。加强对市场和价格监管，加大对粮油肉等重要商品市场监管力度，维护正常市场秩序，严厉打击哄抬价格和乱收费、乱加价等行为。其次，受灾害天气影响，我国南方大部分地区农副产品、能源供应不畅，因此各地区应及时上报受灾地区农副产品及能源市场的供求状况和价格变动情况，保障供应顺畅。再次，保障成品油供应，为应对近期国际原油价格上涨压力，政府应加大补贴力度，缓解成品油供应紧张的矛盾[6]。

参考文献：

[1] 陈东彦，李冬梅，王树忠.数学建模[M].北京：科学出版社，2007

[2] 董臻圃.数学建模方法与实践[M].北京：国防工业出版社，2006

[3] 章绍辉.数学建模[M].北京：科学出版社，2010

[4] 姜启源.数学模型[M].北京：高等教育出版社，2006

[5] 邓薇.MATLAB函数速查手册[M].北京：人民邮电出版社，2010

[6] 刘敏，张燕丽，杨延斌.PPI与CPI关系探析[J].统计研究，2005(2)：24-28

附录：

求解一元线性回归模型中的MATLAB命令：

x=[100.4 101.8 104.7 117.3 117.5 112.3 99.5 99.2 95.6 96.8 101.1 98.3 96.9 100.6 105.0 102.3 103.8]； %输入自变量x的观察值

y=[102.1 103.5 107.5 119.8 124.8 116.6 107.9 102.8 99.7 98.8 101.0 99.8 99.1 103.9 101.3 101.1]； %输入因变量y的观察值

lsline(x，y，′*′) %作拟合直线