Burr Type X分布参数的Bayes可靠性分析*
2014-08-08李兰平
李 兰 平
(湖南财政经济学院 基础课部,长沙 410205)
0 引 言
Burr Type X分布是Burr(1942)最早提出的12种寿命分布之一[1],在可靠性寿命试验和生存分析领域有着重要的应用.关于该分布的统计推断理论引起了很多学者的兴趣.文献[2]讨论了Burr Type X分布次序统计量的单样和双样预测问题;文献[3]讨论了含异常值的Burr Type X分布的Bayes预测问题;文献[4]在平方误差损失函数下讨论了Burr Type X分布作为可靠性寿命模型其失效率函数和可靠性函数的Bayes和经验Bayes估计问题;文献[5]研究了应力和强度均服从Burr Type X分布的应力强度干涉模型可靠度参数的估计;文献[6]研究了刻度Burr Type X分布模型下,应力、强度干涉模型可靠度参数的估计;文献[7]在含有污染数据情形下研究了Burr Type X分布模型下P(Y 设随机变量X为服从参数为θ的Burr Type X分布,相应的概率密度函数和分布函数分别为 f(x;θ)=2θxe-x2(1-e-x2)θ-1,x>0,θ>0 (1) F(x;θ)=(1-e-x2)θ,x>0,θ>0 (2) 其中,θ>0为未知形状参数. Bayes统计作为一类重要统计方法,已经被广泛应用到分布参数的统计推断中[8-10].此处将在平方误差和LINEX损失以及熵损失函数下讨论Burr Type X分布的未知形状参数θ的Bayes估计和经验Bayes估计问题. 设X=(X1,X2,…,Xn)为来自Burr Type X分布(1)的容量为n的简单随机样本,x=(x1,x2,…,xn) 为相应的样本观测值,则给定样本观察值x=(x1,x2,…,xn)后参数θ的似然函数为 (3) 相应的对数似然函数 (4) 在这一部分,将考虑在平方误差损失、LINEX损失和熵损失函数下讨论Burr Type X分布的参数Bayes估计问题. (i) LINEX损失函数最早由Varian(1975)[10]提出,后由Zellner (1986)[11]应用到Bayes估计以及预测问题中,其函数表示形式为 L(Δ)=eaΔ-aΔ-1,a≠0 (5) 在LINEX损失式(5)下,参数θ的Bayes估计为 (6) (ii) 熵损失函数为[12] (7) 在熵损失函数下参数θ的Bayes估计为 (8) 定理1 设X=(X1,X2,…,Xn)为来自Burr Type X分布(1)的样本容量为n的简单随机样本,x=(x1,x2,…,xn) 为相应的样本观测值,t为T的观察值,并设参数θ的先验分布为伽玛分布Γ(α,β),则 (i) 平方误差损失函数下,参数θ的Bayes估计为 (ii) LINEX损失函数下,参数θ的Bayes估计为 (iii) 熵损失函数下参数θ的Bayes估计为 证明由于参数θ的先验分布为共轭伽玛分布Γ(α,β),即相应的概率密度函数为 再由式(3)及Bayes定理,参数θ的后验概率密度函数为 h(θ|x)∝l(θ)·π(θ;α,β)∝ θne-θtθα-1e-βθ∝θn+α-1e-(β+t)θ (9) 从而θ的后验分布为Γ(n+α,β+t),则有 (i) 在平方误差损失函数下,参数θ的Bayes估计为其后验均值,于是参数θ的Bayes估计为 (ii) 由式(9)有 于是在LINEX损失函数下,参数θ的Bayes估计为 (iii) 在熵损失函数下,参数θ的Bayes估计为 在这一部分考虑参数θ的经验Bayes估计问题.以下设参数θ的先验分布为π(θ)=βe-βθ,θ>0,β>0.通过ML-II法获得超参数β的估计,进而可求得参数θ的经验Bayes估计.随机变量X的边缘概率密度函数为 基于m(x;β),得到参数β的最大似然估计为 (10) 从而得到参数θ的经验Bayes估计分别为 (11) 在这一部分,利用Monte Carlo数值模拟一组样本容量为20的样本观测值. 表1 θ=4的容量为20的Burr Type X样本观测值 (2) 给定先验参数值(α,β)=(3.0,1.0),给定a=1和2,计算平方误差损失、LINEX损失和熵损失函数下得到的参数θ的Bayes估计分别为 由表1数值模拟例子和多次数值模拟知,随着样本容量n的增大,最大似然估计、Bayes估计和经验Bayes估计值都越来越接近真值,在有合适的先验分布选用时,建议采用Bayes估计或经验Bayes估计,否则建议采用最大似然估计. 参考文献: [1] BURR I W. Cumulative Frequency Functions[J].Ann Math Statist,1942(13):215-232 [2] SARTAWI H A,ABU-SALIH M S. Bayesian Prediction Bounds for the Burr Type X Model[J].Commun Statist Theory Methods,1991,20(7):2307-2330 [3] JAHEEN Z F. Bayesian Approach to Prediction with Outliers from the Burr Type Model[J]. Microelectron Reliab,1995,35(1):45-47 [4] JAHEEN Z F. Empirical Bayes Estimation of the Reliability and Failure Rate Functions of the Burr Type X Failure Rate Model[J].J Appl Statist Sci,1996,3(4):281-288 [5] AHMAD K E,FAKHRY M E,JAHEEN Z F. Empirical Bayes Estimation of P(Y [6] RAQAD M I,KUNDU D.Comparison of Different Estimators of P(Y [7] KIM C,CHUNG Y. Bayesian Estimation of P(Y [8] 王琪,李玮.对称熵损失函数下两参数广义指数分布形状参数的Bayes估计[J]. 重庆工商大学学报:自然科学版,2012(2):1-4 [9] 任海平,宋允全.两个不同损失函数下一类分布族参数的Minimax估计[J].鲁东大学学报,2009,25(3):201-205 [10] VARIAN H R. A Bayesian Approach to Real Estate Assessment[A].In:FIENBERG S E, ZELLNER A eds:Studies in Bayesian Econometrics and Statistics in Honor of Leonard J[C]. Savage North Holland:Amsterdam,1975:195-208 [11] ZELLNER A.Bayesian Estimation and Prediction Using Asymmetric Loss Functions[J]. J Amer Statist Assoc,1986(81):446-451 [12] 张颂,王德辉.熵损失下定数Progressive删失情形Weibull分布尺度参数的估计[J].吉林大学学报:理学版,2011,50(2):219-2261 极大似然估计
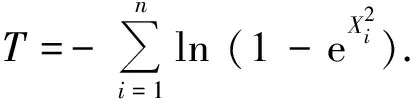
2 Bayes估计
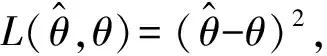

3 经验Bayes估计
4 数值模拟和结论



