网络多agent模型定性分析*
2014-08-08李艳会
李 艳 会
(中山大学 数学与计算科学学院,广州 510275)
1 基础知识
K.Lerman和 O.Shehory[1-4]提出电子交易多agent模型,考虑系统的聚集行为.假定在一个系统中每个agent都给定一个任务,以最低价购买货物;假定所有的 agent都知道提供商品的供应商的位置和商品的零售价,多个 agent可以聚集在一起形成一个大的客户来批发商品,商品的价格随批发量的增多而降低,但有一个最低价格,也就是说批发量有最大值.因此,各 agent到处游走,在各供应商处集聚形成较大的批发商,称之为队列,单个 agent可以自己选择加入哪一个供应商队列,也可以从一个已经形成的批发商处转移到其他批发商处.分析系统中 agent的这些行为,xi是t时刻系统中有i个agent的队列(批发商)的个数,dxi/dt是这种队列的数量变化,xn是最大值队列,ai是结合率,是一个agent加入到有i个agent的队列中去的速率,bi是分解率,是有i个agent的队列中的某个agent离开的速率.建立的模型[1]为(式(1)(n>2))
(1)
其中ai,bi(i=1,2,…,n)为非负常数.
K.Lerman和O.Shehory[1]对所有ai=a,bi=b(i=1,2,…,n)的特殊情形进行了数值仿真,结果如图1所示.从图1 的数值模拟结果,可以发现几个有趣的现象(图1中的ri(t)(1≤i≤n)对应于文中的xi(t)/N).

图1 数值仿真的结果
(1) 当B=0时,结果中x1(t)不存在;
(2) 当B等于某个值时,所有ri(t)都相等;
(3) 从xn>xn-1>…xk>xk-1>…x2>x1变化到xn 另外存在的问题是此系统是否有解.由于各agent是自由的,会不会随处游荡,也就是对应的模型有没有稳定解.这些agent形成的队列(批发商)的规模如何,模型的假设条件是否符合实际,为解决这些问题,对系统进行定性分析. 对一般情形下的系统(1),有定理1-3. 定理1 系统(1)的解xk(t)(k=1,2,…,n)满足关系式 (2) 证明系统(1)的第2式可改写为 (3) 同理系统(1)的第3式,可得 (4) 将式(3)(4)代入系统(1)可得 即 证明系统(1)的平衡点由方程组 (5) 式(5)中,所有2≤k≤n的方程相加可得 x2=(a1/b2)x12 依次代入,可得 代入式(2),可得 定理3 系统(1)运行过程中总有xi(t)≥0(i=1,2,…,n),并且xi(t)不同时为 0,其中x1(t)不会停留在边界上,即使在某时刻tm,x1(tm)=0,x1(t)也不会始终为 0. 证明首先证明在任意时刻t,系统中xi(t)(i=1,2,…,n)不全为0,这由定理1很容易得证.假定某一时刻xi(t)=0(1≤i≤n),下面根据不同i进行分析. (1) 当i=1时,即假定在某时刻t,x1(t)=0,根据系统(1)有 (2) 当i=k(2≤k 因此,在t+Δt时刻就有xk(t+Δt)≥0(Δt→0),不会出现xk(t)<0的情况. (3) 当i=n,即在某时刻t,xn(t)=0,根据系统(1)有 因此,xn(t)≥0,不会出现xn(t)<0的情况. 定理4 整个系统运行过程中,xi一直在第一卦限内部或边缘,当xi(t)=0(2≤i≤n),并且保持dxi/dt=0. 3个定理证明了仅在第一卦限研究系统(1)即可,并且结合式(2)可知,系统(1)的解在第一卦限的一个有界闭区域内.由于此区域内仅有一个奇点,因此,系统的解趋于此奇点或某极限环. K.Lerman和 O.Shehory[1]对系统(1)中ai=a,bi=b时进行了数值仿真,为了简化分析,令B=b/a,τ=at,则系统(1)变为 (6) 下面解释数值仿真结果中的某些现象. 由此说明了数值仿真结果中为什么会出现随着B的增长,系统从xn>xn-1>…>xk>xk-1>…>x2>x1变化到xn 这样,从一般性分析的基础上便可对原系统的数值仿真结果进行说明.图2是定性分析结果,图1是原文的数值仿真.图1中ri含义同图2的xi,横坐标轴是B/N,纵坐标轴是ri/N,也即文中的xi/N.曲线形状是相同的,只是相当于缩小一个比例. 图2 定性分析结果 从上面的分析可以看出,数值仿真的结果可以从原模型中通过定性分析得出,从分析结果验证了模型满足系统假设条件.另外,定性分析严格证明了数值分析中的结论并且分析出一些数值仿真所不能得到的一些特性. 参考文献: [1] LERMAN K,GALSTYAN A. A General Methodology for Mathematical Analysis of Multi-Agent Systems[R]. USC Information Sciences Technical Report IsI-TR-529,2001 [2] LERMAN K,SHEHORY O. Coalition Formation for Large-Scale Electronic Markets[A]. ICMAS-2000[C]. Boston or IBM Research Lab in Haifa,2000 [3] LERMAN K. Design and Mathematical analysis of agent-based system[M]. Berlin:Springer-Verlag,2001 [4] LERMAN K,GALSTYAN A. Mathematical Model of Foraging in a Group of Robots Effect of Interference[J]. Autonomous Robots,2002(13):127-1412 定性分析(一般情形)

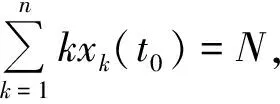


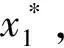
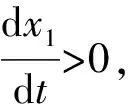

3 定性分析(特殊情形ai=a,bi=b)







