基于无向连通图理论的矩阵集结方案优化*

李 亚 平

(安徽经济管理学院 信息工程系，合肥 230059)

群组决策中，AHP判断矩阵集结是多目标多元素决策的关键问题[1]，它直接影响到由多个判断矩阵形成一致性评价结果的合理性和科学性.针对群组决策中矩阵集结的研究，徐泽水提出了基于可能度的区间数互补判断矩阵排序方案[2]，杨善林、刘心报给出了hadamard加性凸组合和乘性凸组合的集结方法[3]，吴江从偏好信息的角度提出并设计了一种群组区间数互补判断矩阵的集结方法[4]，郭欣荣、吕跃进提出了一种基于无向连通图理论的矩阵集结方案[5].这些集结方案为避免矩阵集结中一致性调整带来的复杂性和主观性，从不同的角度设计了可行的数学方法，文献[6]还对hadamard凸组合的基本性质进行了研究，并对其中乘性集结和加性集结进行了研究.

此处对基于无向连通图理论的矩阵集结方案进行了研究，同时借鉴其他矩阵集结方案的基本思想，论证该方案在专家矩阵偏差及一致性调整方面有相应的优势及存在的问题.对于加性及乘性集结方案，存在集结结果不符合逻辑含义以及在特定情况下出现不一致排序的情形.

1 问题的提出

1.1 基于无向连通图矩阵集结方案的基本思想

按照文献[5]设计的集结方案，其基本思想是对m个N*N的判断矩阵M1，M2，…，Mm进行集结时，首先，在N*N矩阵的上三角(或下三角)中选取N-1个位置，要求在这N-1个位置的每一个位置(i，j)，对应取得的{M1(i，j)，M2(i，j)，…，Mm(i，j)}相对一致，偏差尽量小(其中偏差计算的方法为向量中各元素两两相减的绝对值求和).若将判断矩阵视为图存储结构中的邻接矩阵，此N-1个元素所对应的图结构为无向连通图(即不存在环).简而言之，就是在无环的前提下，不存在其他位置上相应的偏差小于选定的N-1个位置所对应的偏差.对这些位置的元素Aij求算术平均(加性)或几何平均(乘性)，以此为基础，按照行与行成比例的原则，推算其他位置元素值，以此构建具有完全一致性的判断矩阵.

1.2 存在的问题

为更好地描述问题，以文献[5]中的专家判断矩阵为例，给出一个计算范例.

(1)

此处仅对式(1)各矩阵的元素Ai(1，3)=(5，7，8，2)调整为Ai(1，3)=(3，2，2，1/3)，同时对应调整Ai(3，1)位置元素值，形成新的专家判断矩阵：

(2)

对矩阵B1，B2，B3，B4采用文献[ 5]中设计的基于无向连通图理论的集结方法进行集结.

Step 1：群组决策中，判断矩阵会存在不一致的情形[7]，因此需对矩阵B1，B2，B3，B4进行一致性检验，经检验其一致性比率均小于0.1，即符合一致性检验要求.

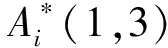
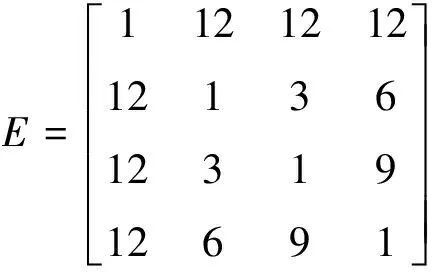
即与原文的偏差矩阵仅在E13位置有差别.

Step 3：由此可以初步判断，B1，B2，B3，B4中一致性较高的元素为各矩阵中的b23，b24，b34，如图1所示.

由于图1存在环，在完全一致性的前提下，按照行与行成比例的原则，无法推导出其他元素值.因此，在上三角的余下元素值中挑选次小的值替换(b23，b24，b34)中最大的b34.由于E中其他位置的值均为12，则有3种替换方案，如图2-图4所示，其中图2，图3与原文方案一致，图4为重新设计的Ai(1，3)=(3，2，2，1/3)所形成.

图1 最小偏差图结构

图2 无环最小偏差图结构1

图3 无环最小偏差图结构2

图4 无环最小偏差图结构3

Step 4：按图4所示方案，对矩阵B1，B2，B3，B4中，一致性较高的(b23，b24，b13)进行乘性集结，得到

按照行与行成比例的原则，推导出上三角其他元素值，并按照互反原则形成最终具有完全一致性集结矩阵：

(3)

对其进行EM法，得排序向量为W=(0.293，0.174，0.207，0.325)，则得到专家排序为S4>S1>S3>S2.同理对图4采用加性集结，同样得到S4>S1>S3>S2的排序结果.

同理，按照图2，图3所示方案，无论按照乘性原则还是加性原则均可以得到的专家排序均为S1>S4>S3>S2，这与原文中所采用的加性方法在图2，图3情况下所得排序一致.

因此，可以得到在特定情况下，基于无向连通图理论的矩阵集结方案可能出现相互矛盾的排序结果.

2 问题分析

之所以出现相互矛盾的排序结果，是因为在基于无向连通图理论的矩阵集结方案中设计的偏差计算方法得到偏差矩阵的e12=e13=e14=12，即各专家矩阵在b12，b13，b14位置的偏差是相等的.因此图2-图4对应的3种方案具有同等的合理性，

然而，基于无向连通图理论的矩阵集结方案计算专家评价偏差方法的基本思想是利用各专家评价值在等级上差值的绝对值和来衡量偏差程度，因此，可以导出如下结论：对于评价值(4，2)和(2，1/2)，按照step 2的规则对应转换为X1=(12，10)和X2=(10，8)，易知二者的等级偏差均为2，但对应的加性集结综合评价值分别为(4+2)/2，(2+1/2)/2，即3和5/4，同理对应的乘性集结综合评价值分别为2.83和1.显而易见，虽等级偏差相等，但前者所包含的一组专家评价在排序上一致的，后者包含的专家评价在排序上相反，同时二者在形成的综合评价值上存在显著偏差.因此，基于无向连通图理论的矩阵集结方案设计的计算专家评价偏差方法仍有改进的空间.

3 优化设计

基于无向连通图理论的矩阵集结方案，在本质上选取一致性较好的专家意见进行加性或乘性集结，在符合判断矩阵一致性的前提下，按照文献[5]设计的等级偏差方法所选取的一致性较好的专家意见可能导致相矛盾的综合排序，因此需要对通过等级偏差来确定专家意见一致性的方法进行优化调整.在等级偏差相等时，按以下原则进行调整：

(1) 首先按照逻辑含义的偏差，在等级偏差相等时，剔除同时包含不同排序专家意见的矩阵位置(即在该位置，多个专家矩阵中同时存在大于1和小于1的评价值).

(2) 对于剩下符合条件的位置大于或等于2个时，则通过比较方差来进行选取.例如，对于评价值(1，2，3，4，5)和(1，1，1，1，6)，按照step 2的规则对应转换为X3=(9，10，11，12，13)和X4=(9，9，9，9，14)的等级偏差均为3.则根据D(X1)=10，D(X2)=20，优先选取X3对应的分支.

(3) 其他情形按基于无向连通图理论的矩阵集结的原方案进行.

由此可以避免基于无向连通图理论的矩阵集结的集结结果不符合逻辑含义以及在特定情况下出现不一致排序的情形.

参考文献：

[1] 陈可.基于判断矩阵的群决策方法研究综述[J].系统工程，2009，27(1)：8-14

[2] 徐泽水.区间数互补判断矩阵排序的一种实用方法[J].运筹与管理，2001，10(1)：16-19

[3] 刘心报，杨善林.判断矩阵的Hadamard凸组合[J].系统工程理论与实践，2000，20(4)：83-85

[4] 吴江.群组区间数互补判断矩阵偏好信息的一种集结方法[J].系统工程理论方法应用，2004，13(6)：500-503

[5] 吕跃进，郭欣荣. 群组AHP判断矩阵的一种有效集结方法[J].系统工程理论与实践，2007(7)：132-136

[6] 徐泽水.文献[1]和[2]中判断矩阵凸组合性质的一个注记[J].系统工程理论与实践，2001(1)：139-140

[7] 陈均明.模糊层次分析法在投资决策中的应用[J].重庆工商大学学报：自然科学版，2008，25(1)：29-32