结构参数对局部弹性翼型气动性能的影响规律

雷鹏飞,张家忠,贾艳俊

(1.西安交通大学能源与动力工程学院,710049,西安; 2.陕鼓动力股份有限公司,710075,西安)

结构参数对局部弹性翼型气动性能的影响规律

雷鹏飞1,张家忠1,贾艳俊2

(1.西安交通大学能源与动力工程学院,710049,西安; 2.陕鼓动力股份有限公司,710075,西安)

采用数值方法研究了低雷诺数下局部弹性翼型结构参数对翼型性能及流动结构的影响。建立了局部弹性结构的振动模型,采用具有双时间步长的任意拉格朗日-欧拉方法和基于特征线的算子分裂法对非定常流固耦合问题进行数值模拟,对不同的结构密度、弹性模量、阻尼下局部弹性翼型的升力以及结构振动的频率特性进行了分析。研究结果表明:局部弹性结构自激振动对流动的控制存在最佳的振动频率范围;在合适的结构参数下,如较小的结构弹性模量和结构阻尼,局部弹性结构能够产生较大振幅的自激振动,从而改变流动结构并提高翼型升力;对于具有高升力的局部弹性翼型,结构振动能够显著改变非定常流动分离模式,减小分离区域,达到抑制分离、提高翼型升力的效果。

局部弹性;自激振动;双时间步长;结构参数

近年来,随着对翼型、叶片等性能要求的提高,许多主动或被动的流动控制手段被提出,如吹吸气、声激励、结构振动等,并通过实验及数值方法验证了非定常小扰动对流动控制的可行性[1-2]。近年来的研究表明,翼型局部结构在非定常气动力下做出适当的振动能够改善流动状态,从而提高翼型升力或减小其阻力[3]。弹性结构的自激振动能够利用其自身的自适应性,实现对流动的控制,然而由于非定常流动及其控制的复杂性,弹性结构振动对流动的控制机理仍不明确。

早期对翼型振动的研究发现,当翼型在失速攻角附近做俯仰振动时,会产生动态失速,并使失速角推迟[4-6]。然而,由于翼型整体振动会导致结构的断裂等问题,对动态失速的研究主要针对于飞行器等变工况时出现的一系列流动现象及相应的控制手段。随着材料的发展和人们对气动弹性的深入了解,弹性结构的振动逐渐被应用到流动控制中。Smith和Shyy等建立了弹性薄膜与流体之间的耦合模型,并研究了在非定常来流中薄膜翼型的响应[7-8]。随后,Persson等采用高阶间断Garlerkin方法研究了固定和振动的薄膜翼型[9]。Gordnier建立了高精度的二维弹性薄膜翼面的流固耦合问题,数值验证了弹性翼面的振动对翼型升力的提高[10]。康伟和张家忠等提出了局部弹性翼型模型,发现在失速攻角附近,局部弹性结构的自激振动能够大幅提高翼型升力,并且推迟了失速攻角[3,11]。雷鹏飞等采用数值方法研究了低雷诺数下局部弹性翼型的增升效应,着重对其中具有增升效应的非定常流动分离进行了详细分析[12]。然而,在局部弹性结构的自激振动中,不同的结构参数会产生不同形式的结构振动,从而对流动结构及翼型气动性能产生不同的影响,因此本文在文献[12]的基础上,数值模拟了不同结构参数下翼型的气动性能及其流动结构,分析了局部弹性结构的自激振动提高翼型性能的机理。

1 非定常流动的数值求解

局部弹性翼型绕流问题是具有动边界的流固耦合非定常流动问题,因此可以采用任意拉格朗日-欧拉方法(Arbitrary Lagrangian Eulerian,ALE)和基于特征线的算子分裂法(Characteristic Based Split scheme,CBS)[13-15]对这一类问题进行求解。

本文所研究的流动马赫数远小于0.3,因此可以看作是不可压缩流动。定义翼型弦长L为特征长度,来流速度U为特征速度,其他变量如坐标、时间、压力、速度等均可以转化为无量纲形式如下

(1)

式中:x、y为笛卡尔坐标;ρf为流体密度;p为压力;ui为速度。为了简便,将式(1)中变量的上标*略去。在ALE坐标下,不可压缩N-S方程可以表

(2)

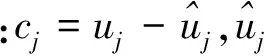
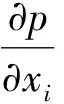
(3)

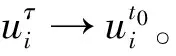
在虚拟时间上采用CBS算法对控制方程式(3)进行分步求解:

(1)忽略压力项和∂ui/∂t,得到中间速度

(4)

(2)根据中间速度求解压力

(5)

(3)根据压力项和∂ui/∂t修正速度

(6)

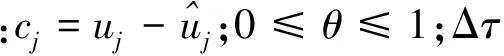
2 局部弹性结构振动的数值求解

二维翼型表面局部弹性结构可以看作是两端简支且具有一定厚度的浅拱[16],在非定常气动力的作用下,能够产生自激振动,如图1所示。

图1 浅拱结构示意图

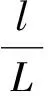
(7)

式中:l为浅拱弦长;h为浅拱的厚度;w为浅拱在垂直于弦长方向的位移;ρs为浅拱密度;E为弹性模量;F为浅拱所受的气动载荷。为了简便,将式(7)中变量的上标*略去,因此浅拱控制方程的无量纲形式可以表示为

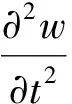
(8)

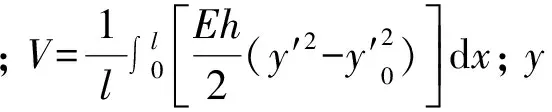
浅拱的简支边界条件和初始条件为

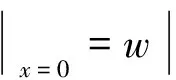
(9)

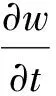
(10)

根据浅拱控制方程的线性算子及边界条件,可以将浅拱的振动分解为各阶振型的振动,即

(11)

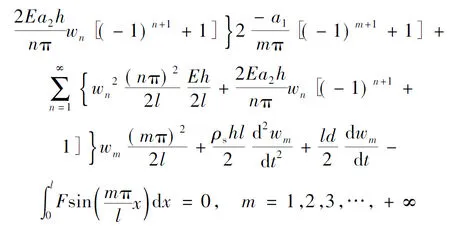
(12)

然后,采用4阶龙格库塔法对方程(12)进行求解,即可得到每阶振动模态的幅值。本文中k=4,并选取前10阶模态对浅拱的振动进行逼近。

3 数值方法的验证

为了验证弹性结构振动及其与流体耦合相关算法的准确性,对具有柔性底面的方腔顶盖驱动流进行了数值模拟。该问题的模型及参数如图2a所示,本文采用浅拱来模拟柔性底面的振动。柔性薄板中点随时间的位移如图2b所示,可以看出所得结果与Bathe等所得结果[17]吻合,验证了本文所采用的浅拱模型求解弹性结构自激振动问题的准确性。

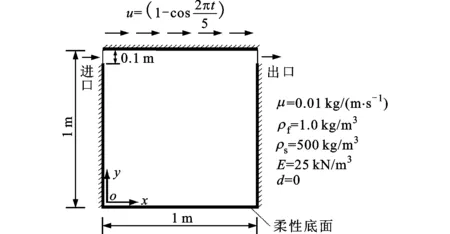
(a)方腔流动模型及相关参数[17]

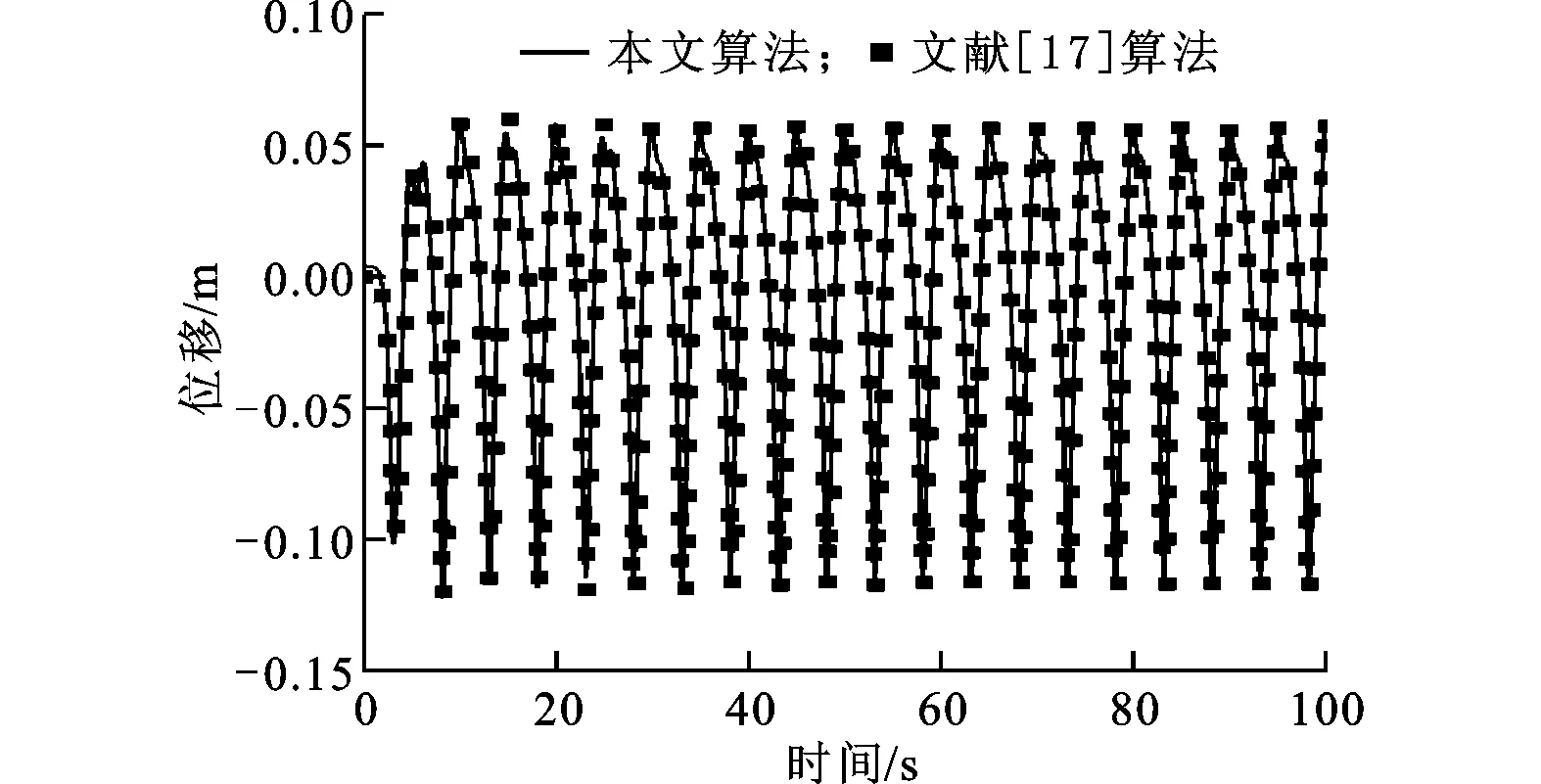
(b)弹性薄板中点随时间的位移

4 结果及分析

文献[12]研究了具有局部弹性结构的NACA0012翼型(结构参数如表1所示)在Re=5 000时不同攻角下的升力系数(CL)和阻力系数(CD),如图3所示。可以看出,翼型在攻角为6°时具有较明显的增升效应。因此,本文选取Re=5 000、攻角为6°,局部弹性结构位于翼型上表面0～0.1L弦长处,如图4所示。本文主要研究结构密度ρs、结构阻尼d和弹性模量E对翼型性能及相应的流动结构的影响,其中结构参数的选取如表1所示。

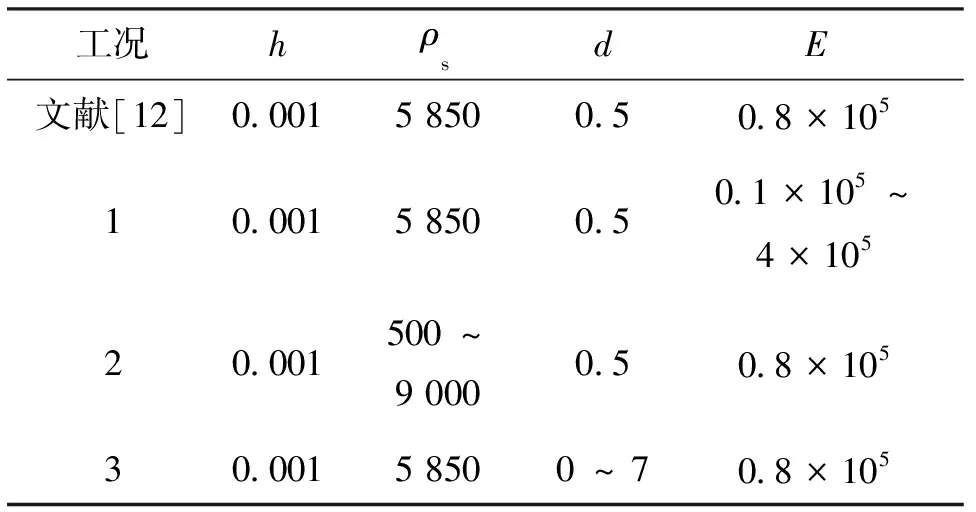
表1 无量纲结构参数的选取

注:工况1～3分别对应本文选取的弹性模量、结构密度和阻尼组合。

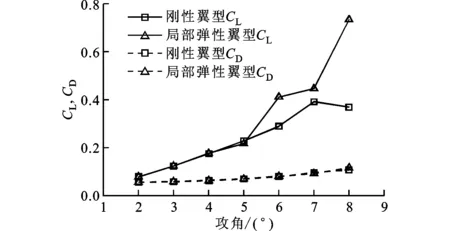
图3 不同攻角下局部弹性结构对翼型升阻力系数的影响[12]

图4 翼型局部弹性结构示意图

4.1 局部弹性结构的振动特性

图5 攻角为6°时浅拱前3阶振型的振动状态

在非定常气动力作用下,局部弹性结构发生变形,并产生自激振动。图5为攻角为6°、结构参数同文献[12]时浅拱前3阶振动模态的幅值。从图中可以看出,浅拱的振动以第一阶振型的振动为主,而且每阶振型的幅值在新的平衡位置随时间做幅度为A的周期振动,如图5所示。图6为局部弹性结构振动中的平均位置和最大位移位置,相对于翼型的尺寸,其振动幅值较小。在结构的自激振动中,结构振动的频率取决于非定常气动力,因此流场频率与结构振动频率保持一致。

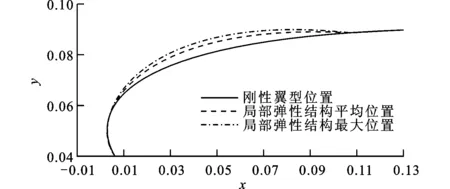
图6 攻角为6°时浅拱的振动平均位置与最大位移

4.2 不同结构参数下翼型升力及结构振动特性

对不同结构参数下的翼型升力、结构振动的幅度和主频率f(无量纲频率,f*=Lf/U,上标省略)进行了比较,分析了局部弹性结构自激振动提高翼型升力的主要因素。

4.2.1 结构弹性模量 当结构弹性模量减小时,结构在相同的气动力下能够产生更大幅值的振动,从而对流场产生较大的影响。图7为翼型升力和结构振动特性随弹性模量的变化。从图7a中可以看出,较小的结构弹性模量具有较好的增升效果(E<105),当结构的弹性模量较大时,翼型升力也有所提高,但效果并不明显。对比翼型升力和结构振动幅值(如图7b所示)可以看出,较大的振动幅值总能够产生较高的翼型升力,尤其是当A>0.002时,翼型升力有着大幅度的提高。然而,当弹性模量过小时,结构的振动幅值急剧增大,如E=104时第一阶振型的振幅是E=5×104时的50倍,但相应的翼型升力仅比后者提高了大约5%。考虑到较大的结构振动幅值容易对结构强度造成负面影响,需要选取适当的弹性模量(E≈5×104)。

从结构振动的主频率随弹性模量的变化(图7c)中可以看出,结构振动频率随结构弹性模量的减小而减小,而振动幅值则随之增大。当结构弹性模量E<105时,f<1.4,翼型具有较大的振动幅值和较高的升力。当结构弹性模量E>2×105时,频率大于刚性翼型的主频率,f≈1.8,翼型升力仅有小幅度的提高。

(a)翼型的升力

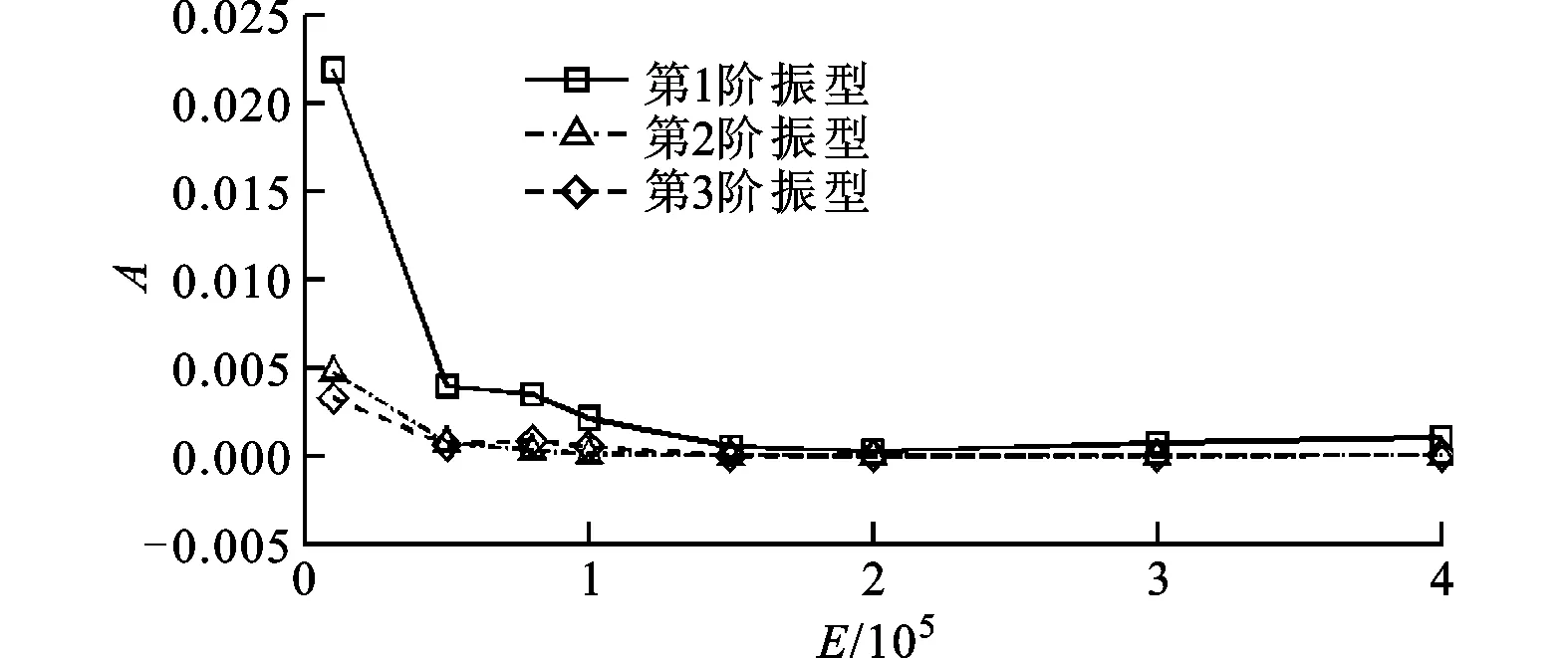
(b)结构振动幅值

(c)结构振动主频率

4.2.2 结构密度 不同结构密度下的翼型升力及结构振动特性如图8所示。从图中可以看出,在结构密度为6 000左右时结构振动幅值达到最大值,同时翼型具有较好的增升效果。从结构振动主频率随结构密度的变化中可以看出,随着密度的增大,振动的主频率呈减小趋势,当f<1.4时,结构振幅显著增大,翼型升力也相应地提高。然而,当ρs>8 000时结构振动幅值接近于0,振动主频率与刚性翼型主频率接近。当ρs=4 000时,结构振动主频率大于刚性翼型的主频率,结构振动幅值虽然小于ρs=5 000时的振动幅值,但翼型升力却高于后者,该情况与E>4×105时相似,意味着当结构振动频率大于刚性翼型主频率时,即f≈1.8,结构振动同样能够提高翼型升力,但由于自激振动的幅值较小,增升效应相对于f<1.4时较弱。

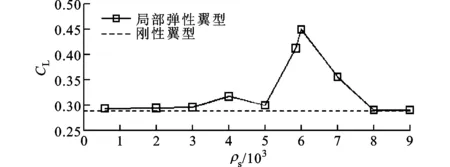
(a)翼型的升力

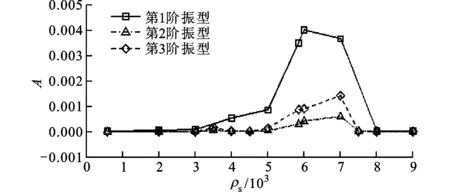
(b)结构振动幅值

(c)结构振动主频率

4.2.3 结构阻尼 图9为不同阻尼下翼型升力和结构振动特性,可以看出,随着结构阻尼的增大,结构振动幅值逐渐减小,相应的翼型的升力也随着结构振动幅值的减小而减小。从结构振动主频率(如图9c所示)上看,具有高升力的翼型结构振动频率在1.2～1.4之间。当d=0.5～2时,f≈1.4,但较大的结构阻尼d>1使得结构振动幅值急剧减小,抑制了翼型升力的提高。

综上所述,在局部弹性结构的自激振动中,较大的振动幅值(A>0.002)能够产生较好的增升效应,然而只有当结构振动频率f=1.2～1.4时,结构才能产生振幅较大的振动。该现象说明流场中存在一定的频率范围,适当结构参数下的局部弹性结构能够在该频率范围内与流场耦合激发较大振动幅值的自激振动,从而产生足够大的扰动来改变流动结构,并提高翼型的升力,体现了局部弹性结构的自适应性。

4.3 具有增升效应的非定常流动结构

(a)翼型的升力

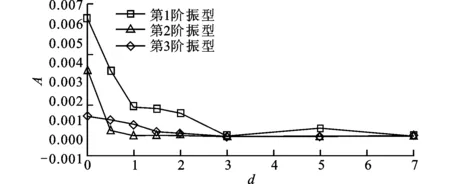
(b)结构振动幅值

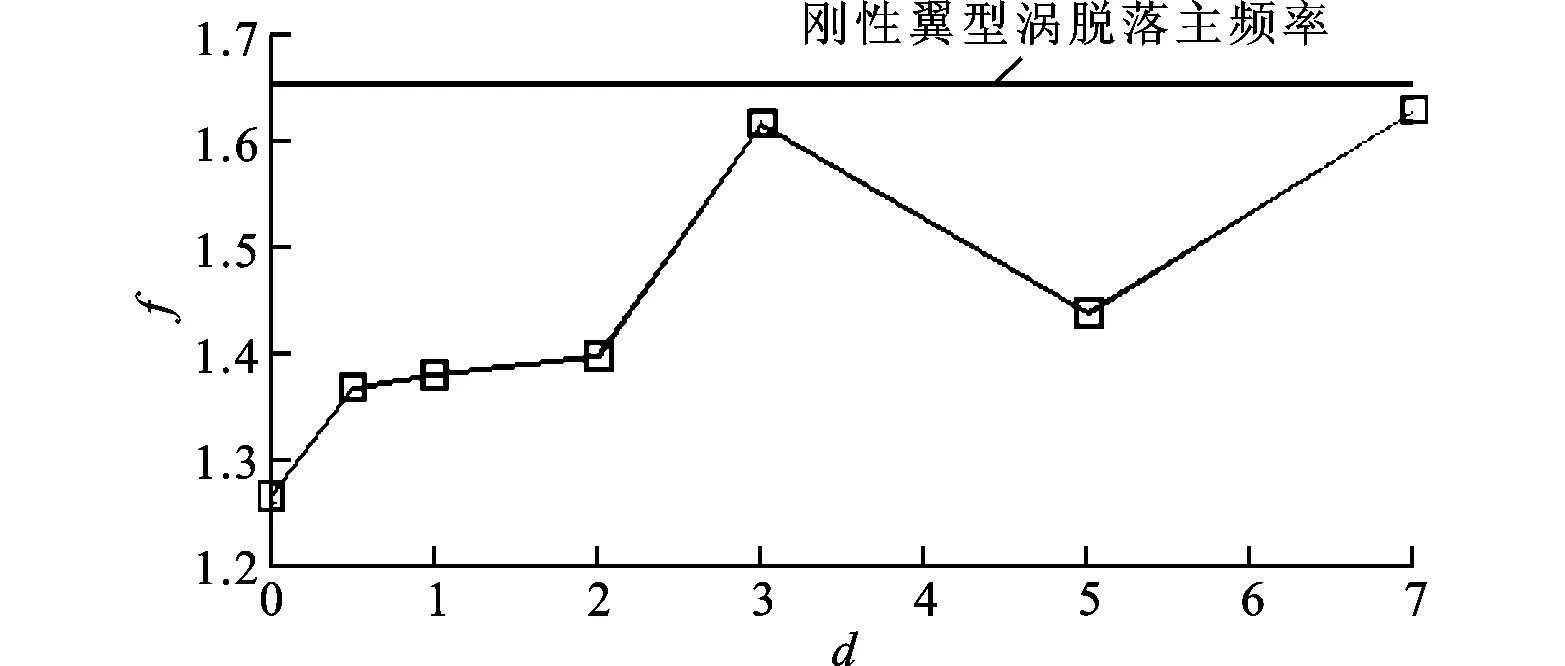
(c)结构振动主频率

(a)瞬时流场 (b)时均流场

图10为部分具有大振幅、高升力翼型绕流中的瞬时流线图(图10a)及相应的时均流线图(图10b),除图中标识的结构参数外,其他参数同文献[12]。从瞬时流线图来看,具有增升效应的翼型,其流场也具有相似结构,即翼型上表面具有若干个小尺度的分离泡,而对应的刚性翼型绕流中仅存在一个较大的分离区域。由时均流线图可知,局部弹性结构的振动使得分离区大幅减小,从而提高了翼型升力。图11为E=8×104时流动结构及涡量分布随时间的变化,图中T为流场的周期,可以看出在翼型上表面,小尺度的分离泡周期性地从翼型前缘产生并逐渐向下游移动,并在移动过程中诱发产生具有涡量集中的旋涡,该旋涡具有较低的压力分布,从而能够降低翼型上表面的压力,提高翼型升力。图12为翼型升力和结构第一阶模态振动幅值随时间的变化,结合图11的流场演化过程可以看出翼型升力在t=0.2T时达到最大值;随后翼型上表面靠近尾部的旋涡开始脱落,导致翼型升力下降;当t>0.6T时,翼型前缘新生成的分离泡开始向下游移动,并在其附近形成涡量集中的旋涡,从而使翼型升力又开始逐渐增大。

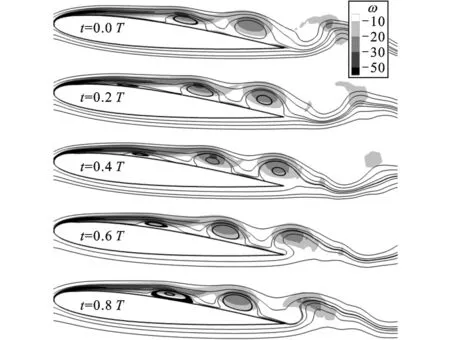
图11 E=8×104时翼型附近非定常流动结构随时间的变化规律

图12 E=8×104时翼型升力和结构第一阶模态振动幅值

由于分离泡产生的频率与结构振动频率相同,每个结构振动周期内都会产生一个独立的分离泡,结构振动频率的变化将影响到翼型表面移动分离泡和旋涡的大小、数量和分布,因此合适的结构振动频率和足够大的振动幅值是提高翼型升力的主要因素。在实际应用中,局部弹性结构的振动效果受到结构材料的限制,因此可以对结构施加一定频率和幅值的强迫振动来弥补结构材料的限制,达到提高翼型性能的目的。

5 结 论

本文通过数值方法研究了局部弹性翼型绕流中结构参数对翼型升力及流动结构的影响。数值模拟结果表明,局部弹性结构的自激振动对流动的控制存在最佳的振动频率范围,在合适的结构参数下,非定常气动力能够使弹性结构产生较大振幅的自激振动,从而改变非定常流动结构,提高翼型升力。对于具有高升力的局部弹性翼型,其流动结构具有与刚性翼型截然不同的非定常流动分离模式,该流动分离模式中存在多个独立的小尺度分离泡,能够有效地减小分离区域,达到抑制分离、提高翼型升力的效果。结构参数中,较小的结构弹性模量和结构阻尼能够更好地激发结构的自激振动,有利于流动的控制和翼型升力的提高。

[1] GREENBLATT D,WYGNANSKI I J.The control of flow separation by periodic excitation [J].Progress in Aerospace Sciences,2000,36(7): 487-545.

[2] 战培国,程娅红,赵昕.主动流动控制技术研究 [J].航空科学技术,2010(5): 2-6.

ZHAN Peiguo,CHENG Yahong,ZHAO Xin.A review of active flow control technology [J].Aeronautical Science and Technology,2010(5): 2-6.

[3] KANG W,ZHANG J Z,FENG P H.Aerodynamic analysis of a localized flexible airfoil at low Reynolds numbers [J].Communications in Computational Physics,2012,11(4): 1300-1310.

[4] MCCROSKEY W J,CARR L W,MCALISTER K W.Dynamic stall experiments on oscillating airfoils [J].AIAA Journal,1976,14(1): 57-63.

[5] WANG C M,WU J C,SANKAR L N.Unsteady aerodynamics of airfoils oscillating in and out of dynamic stall [C]∥AIAA 3rd Applied Aerodynamics Conference.Reston,VA,USA: AIAA,1985: 4078.

[6] WU J Z,LU X Y,DENNY A G,et al.Post-stall flow control on an airfoil by local unsteady forcing [J].Journal of Fluid Mechanics,1998,371: 21-58.

[7] SMITH R,SHYY W.Computation of unsteady laminar flow over a flexible two-dimensional membrane wing [J].Physics of Fluids,1995,7(9): 2175-2184.

[8] SHYY W,SMITH R.A study of flexible airfoil aerodynamics with application to micro aerial vehicles [C]∥AIAA 28th Fluid Dynamics Conference.Reston,VA,USA: AIAA,1997: 1933.

[9] PERSSON P O,PERAIRE J,BONET J.A high order discontinuous Galerkin method for fluid-structure interaction [C]∥18th AIAA Computational Fluid Dynamics Conference.Reston,VA,USA: AIAA,2007: 4327

[10]GORDNIER R E.High fidelity computational simulation of a membrane wing airfoil [J].Journal of Fluids and Structures,2009,25(5): 897-917.

[11]康伟,张家忠.翼型局部弹性自激振动的增升减阻效应研究 [J].西安交通大学学报,2011,45(5): 94-101.

KANG Wei,ZHANG Jiazhong.Numerical analysis of lift enhancement and drag reduction by self-induced vibration of localized elastic airfoil [J].Journal of Xi’an Jiaotong University,2011,45(5): 94-101.

[12]雷鹏飞,张家忠,陈嘉辉.局部弹性翼型非定常分离的动力学特性 [J].力学学报,2012,44(1): 13-22.

LEI Pengfei,ZHANG Jiazhong,CHEN Jiahui.Unsteady separation of flow around airfoil with local elastic structure [J].Chinese Journal of Theoretical and Applide Mechanics,2012,44(1): 13-22.

[13]NITHIARASU P.An arbitrary Lagrangian Eulerian (ALE) formulation for free surface flows using the characteristic-based split (CBS) scheme [J].International Journal for Numerical Methods in Fluids,2005,48(12): 1415-1428.

[14]GAITONDE A L.A dual-time method for two-dimensional unsteady incompressible flow calculations [J].International Journal for Numerical Methods in Engineering,1998,41(6): 1153-1166.

[15]WANG Y T,ZHANG J Z.An improved ALE and CBS-based finite element algorithm for analyzing flows around forced oscillating bodies [J].Finite Elements in Analysis and Design,2011,47(9): 1058-1065.

[16]ZHANG J Z,LIU Y,LEI P F,et al.Dynamic snap-through buckling analysis of shallow arches under impact load based on approximate inertial manifolds [J].Dynamics of Continuous,Discrete and Impulsive Systems: Series B,2007,14(5): 287-291.

[17]BATHE K J,ZHANG H.A mesh adaptivity procedure for CFD and fluid-structure interactions [J].Computers & Structures,2009,87(11/12): 604-617.

(编辑 刘杨 葛赵青)

InfluencesofLocalFlexibleAirfoilParametersonAerodynamicPerformance

LEI Pengfei1,ZHANG Jiazhong1,JIA Yanjun2

(1.School of Energy and Power Engineering,Xi’an Jiaotong University,Xi’an 710049,China;2.Xi’an Shaangu Power CD.LTD.,Xi’an 710075,China)

The influences of structure parameters of airfoil with local flexible structure on the performance and flow structure under low Reynolds number are investigated numerically.The local flexibility model is established,the unsteady fluid-structure interaction is simulated by arbitrary Lagrangian-Eulerian method (ALE) and characteristic-based split (CBS) scheme with dual time step.The results indicate that there is an optimal range of oscillation frequency and amplitude,at which the airfoil lift can be enhanced remarkably.With proper structure parameters,such as small elasticity modulus and structural damping,the coupling between structure and fluid leads to large amplitude oscillation to change the flow structure and to enhance lift.For the cases with high lift enhancement,the structure oscillation facilitates changing flow pattern and reducing separated region to suppress flow separation and enhance airfoil lift.

local flexibility; self-induced oscillation; dual time step; structure parameters

2013-11-25。

雷鹏飞(1984—),男,博士生;张家忠(通信作者),男,教授。

国家“973计划”资助项目(2012CB026002);国家“863计划”资助项目(2012AA052303)。

时间:2014-04-30

10.7652/xjtuxb201406019

V211.3

:A

:0253-987X(2014)06-0110-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140430.1754.002.html