基于量子免疫克隆的压缩感知数据重构算法❋

祁 浩，刘洲洲

（1.西北工业大学电子信息学院，西安710072；2.西安航空学院，西安710077）

基于量子免疫克隆的压缩感知数据重构算法❋

祁 浩1，刘洲洲2

（1.西北工业大学电子信息学院，西安710072；2.西安航空学院，西安710077）

提出了一种基于量子免疫克隆的压缩感知数据重构算法（Q-CSDR）。算法先提出了一种能够提高数据重构概率的自适应分帧方法，然后利用量子克隆免疫算法的优化组合性能实现数据的精确重构。实验结果表明，Q-CSDR算法能够根据原始信号稀疏度自动调节压缩比率，具有重构速度快，重构精度高，能够适应于高稀疏度数据重构等优点。该算法已应用于秦始皇帝陵博物院野外文物安防系统。经实际检验，收到了良好效果。

量子免疫克隆；压缩感知；数据重构；稀疏度

1 引 言

压缩感知（Compressed Sensor，CS）［1］是近几年来数据和信号处理的研究热点之一，它使用线性变换将具有一定稀疏度的信号投影到一个低维空间上，并通过使用非线性方式对数据进行重构。压缩感知的优点在于其突破了奈奎斯特采样定理和香农理论的限制，能够以远小于经典采样方法获取的数据量重构出高质量的原始信号，与传统压缩方法相比，压缩感知具有采样数量少、采样数据小等优点。

数据重构算法是压缩感知过程中的一个重要环节，其关键问题在于如何快速、准确的从已知低维数据中恢复出高维数据。目前压缩感知数据重构算法主要分为两类［2］：第一类算法是基于最小化l1范数的算法，包括基追踪算法（Basis Pursuit，BP）［3］，线性规划算法（Linear Programming，LP）［4］等，这类算法具有重建精度高的优点，但其算法的复杂度较高，且执行效率低，实用性较差；第二类是基于最小化l0范数的方法，即贪婪算法，包括正交匹配追踪算法（Orthogonal Matching Pursuit，OMP）［5］、子空间追踪算法（Subspace Pursuit，SP）［6］、压缩采样匹配追踪算法（Compressive Sampling Matching Pursuit，Co-SaMp）［7］、迭代硬阈值算法（Iterative Hard Thresholding，IHT）［8］、基于感知字典的迭代硬阈值算法（Sending Dictionary-based Iterative Hard Thresholding，SDIHT）［9］、基于混沌量子免疫克隆算法的正交匹配算法（Orthogonal Matching Pursuit based on Quantum-inspired immune clonal，OMP-QICA）［10］、基于遗传算法的压缩感知重构算法［11］等，这类算法主要通过迭代更新当前估计来优化信号恢复情况，在原始信号稀疏度较小的情况下具有很好的重构精度及重构速度，但对于稀疏度较高的原始信号其算法的性能却有明显下降。针对此问题，本文提出了基于量子克隆免疫算法的压缩感知数据重构算法（Quantum-inspired immune clonal based Compressed sensor data reconstruction，Q-CSDR）。Q-CSDR算法利用量子克隆免疫算法的快速搜索性能以及快速收敛能力实现了对原始数据的精确重构，使用自适应长度分帧方法减少l1范数最小化问题的冗余解，提高了高稀疏度条件下数据的重构精度。实验结果表明，该算法具有重构精度高、重构性能稳定等优点。

2 压缩感知与数据重构

设X∈RN为长度为N的一维信号，压缩感知过程可以用公式（1）来表示，Φ为M*N维的观测矩阵（M＜＜N）：Y＝ΦX。通过观测矩阵对x进行观测，可以将原始信号压缩为长度为M的一维信号，实现数据压缩。如何利用已有的感知数据Y重构出原始信息，并要求重构信号尽可能逼近原始信号，是压缩感知理论框架中最关键的操作之一。压缩感知信号重构问题实际上是个求解欠定方程组的过程，数学表达过程如公式（1）所示：

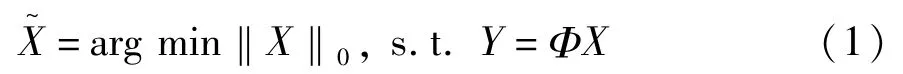
其中对于向量x，其lp范数定义为：

在实际重构过程中一般允许存在一定的误差，所以上式可表示成公式（3），其中ε为极小常量：

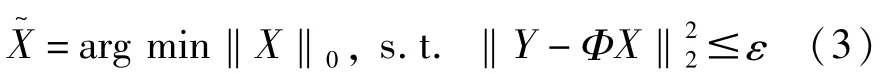
压缩感知重构最关键的问题在于，公式（1）和公式（3）均是数值不稳定的NP-完全问题，在求解过程中需要穷举原始信号x中非零元素位置的种可能组合。

3 基于量子免疫克隆的压缩感知数据重构算法

量子免疫克隆算法（Quantum-inspired immune clonal algorithm，QICA）［12-13］是目前的研究热点之一，是解决NP-完全问题的高效算法，具有很好的优化组合性能。QICA将量子搜索机制和免疫算法克隆选择原理相结合，利用量子编码的叠加性构造抗体，利用克隆操作产生原始种群和克隆子群实现种群扩张，使搜索空间扩大，提高了局部搜索能力；同时借助全干扰交叉操作避免陷入局部最优。

QICA采用了多状态量子比特编码方式和通用的量子旋转门操作，引入动态调整旋转角机制和量子交叉［14］。QICA算法的核心思想是，先使用量子位和量子叠加态生成具有极大随机性的变量值，并利用遍历对解空间的所有变量值进行优化搜索，再通过交叉和量子门旋转避免局部最优，最后，通过线性变换将获得的最优解还原到原优化空间中。

虽然量子克隆免疫算法具有很好的优越性，但原始信号的非零元素位置组合数量巨大，降低了算法的运算速度，因此将量子克隆免疫算法应用于压缩感知需要解决的最关键问题是减少解空间中的冗余解，提高信号重构概率，在对信号压缩前需要对其进一步进行分帧处理。

3.1 分帧方法

假设信号采集端采集的原始信号长度为N，稀疏度为K，根据非零元素的个数将原始信号分为frame＝ceil（K／n）个帧，n为每个帧内包含的非零元素个数，ceil（·）为向上取整函数。自适应分帧方法为：从原始信号的第一位起，记录非零元素的个数m，当m为第τ*n＋1个非零元素时，将其划分为下一帧的起始元素。其中τ为正整数，其取值范围为［0，frame-1］。举例说明：

假设原始信号的稀疏向量x为：

0 0 0 1 1 1 0 1 0 1 0 1 0 0 1 0 0 0 1 0 1 1 0 1 0 0 1 0 0 0

则当n＝2时，可分成如下六个帧：

0 0 0 1 1｜1 0 1 0｜1 0 1 0 0｜1 0 0 0 1 0｜1 1 0｜1 0 0 1 0 0 0。

其原始信号长度为30，稀疏度K＝40。

这种分帧方法的特点是除第一帧外，其余所有帧的起始位均为非零元素。与传统的固定长度分帧方法相比，这种自适应长度的分帧方法减少了重构过程中非零元素个数的排列组合可能性，提高了原始信号的重构概率。

3.2 理论分析

假设信号采集端采集的原始信号长度为N，信号稀疏度为K，则原始信号中的非零元素的可能位置有种可能，设其幅值均匀分布在［rangemin， rangemax］上，则根据概率论相关知识可知：其重建概率：

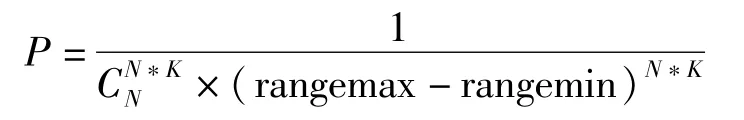
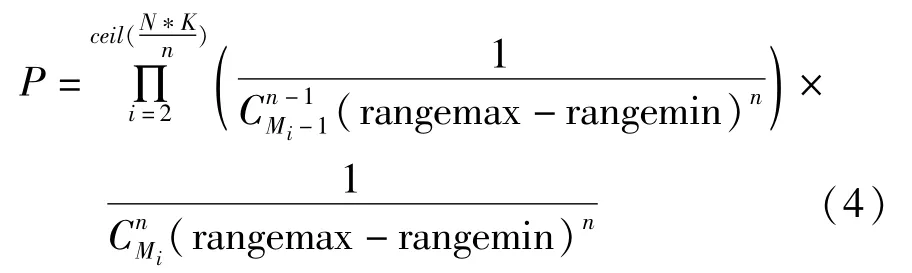
以原始信号为例，表1显示未分帧及分帧后的原始信号x中非零元素的位置组合数量。

表1 分帧前后非零元素位置组合数量

可以看出，随着分帧内非零元素n变大，原始信号中非零元素位置的组合数量也随之迅速增大。n＝1时非零元素位置组合仅有4种，其精确重构的概率最大，但应用于实际过程中会因为分帧长度过短导致帧数量增加，分帧数量增加会导致通信包数量急剧增加，造成网络拥塞，使分帧方法的实用性降低。当n取值过大时，虽然能够减少通信包数量，降低通信开销，但也会造成非零元素位置组合数量急剧增加，降低了数据的重构概率，因此表1仅列出了n＝1～4的非零元素位置组合数量。

3.3 信号重构过程

根据量子免疫克隆理论，我们将压缩感知信号重构过程分为以下四个过程。

3.3.1 权值抗体初始化

量子免疫克隆算法是基于量子计算和遗传算法组成的，其抗体的编码方式采用量子比特编码。一个抗体中量子位的状态是不确定的，可以为0或1，其状态表示为公式（5）：

其中α，β表示相应状态出现概率的两个复数，其关系为α2＋β2＝1。

具有m个量子比特位的抗体可以描述为公式（6）：

其中t表示种群代数。结合信号重构的应用实际，m表示分帧长度。规模为n的量子种群表示为：，Q（t）即为信号重构的解空间。

3.3.2 抗体编码

这里摒弃经典量子理论的坍塌观测解码方法，对公式（6）中的量子位采用文献［8］进行实数编码，其规则如下：

frame为原始信号的分帧数量，xi表示当前帧中第i个位置元素的幅值大小。

在进行实数编码后，算法按照当前分帧的非零元素数量按下列方法，将其权值置为0；

1.若是第一分帧，则按照非零元素个数随机生成位置估计；

2.若不是第一分帧，则估计帧中第一位设为非零元素，其余非零元素位置随机生成。

3.3.3 抗体种群克隆

公式中，mi为种群中第i个抗体的克隆规模，nc是与克隆规模相关且大于种群规模N的常数，本算法中设置为种群规模的1.2倍，f（qi）为第i个抗体的适应度。

3.3.4 抗体种群更新

量子克隆免疫算法中，量子抗体通过量子旋转门和全局交叉来实现更新操作。采用的量子旋转门如公式（9）：

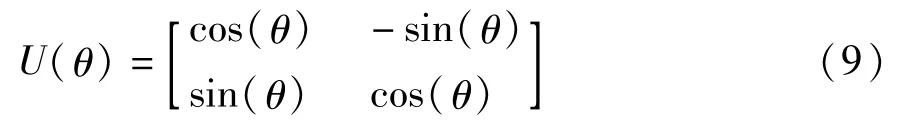
在利用量子旋转门进行更新的基础上，为了构造更加健壮的交叉操作，避免算法陷入局部最优，算法采用了全干扰交叉操作。假设一个种群包含5个长度为8的抗体，其具体交叉方法见表2。

表2 全干扰交叉操作

3.4 算法步骤及流程

算法流程图如图1所示。

图1 算法流程图

算法具体过程如下：

1.将原始信号进行分帧处理，记录分帧长度、帧序列号、稀疏度等信息。

2.种群初始化。设置算法相关参数，包括种群规模sizepop，算法最大迭代次数maxgen或适应度值下限ε，各帧稀疏度sparseratio，并根据压缩前后帧长通过查表确定观测矩阵Φ。

3.根据预置参数初始化种群，种群中每个抗体的稀疏度均为sparseratio。

4.将公式（4）计算得到的输出y与目标输出target带入公式（10）计算适应度，这里设目标输出为n维向量：

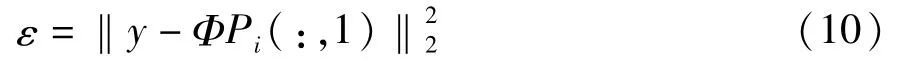
5.对原有种群进行克隆及更新操作，计算新种群的适应度值，保留新种群中前sizepop个最优个体组成下一代种群。

6.若没有达到算法停止条件，则记录当前最优个体及最优结果，然后转向步骤3，若达到停止条件，则输出最优个体及最优适应度值。

7.若还有分帧需要构建，则转向步骤1，反之转向步骤8。

8.将恢复的各帧按帧序列号组合即完成信号重建过程。

4 实验及分析

试验场地选择在秦始皇帝陵博院K9801号坑旁，使用无线传感器作为信号采集设备对监测区域内的微地震信号进行采集。采集到的信号在传感器节点本地进行滤波、降噪等处理后，再通过分帧和压缩后传输至远端服务器。为使对比结果明显可靠，在现场布置两类传感器：一类是传输压缩信号的传感器，一类是传输未压缩信号的传感器。

4.1 自适应长度分帧结果分析

从分析结果可以看出，信号的恢复精度实际上受帧内非零元素个数影响较大，算法的复杂度则受帧长度影响。根据以上结果，对原始信号采取自适应的分帧方法进行处理。实验结果如图2所示。

图2 n＝2时的数据恢复结果

当n＝2时，原始数据共分为22个帧，信号压缩比为200：59，近乎达到3：1。考虑通信中，每帧数据包需要额外增加两个字节原始帧长度和稀疏度信息，因此实际数据压缩比率为162：400＝0.405。重建信号的精度为100%。

如图3所示，当n＝3时，原始数据共分为15个帧，信号压缩比为200：59，约为3：1。考虑通信中，每帧数据包需要额外增加两个字节原始帧长度和稀疏度信息，因此实际数据包长度压缩比率为148：400＝0.37。重建信号的精度为98%。

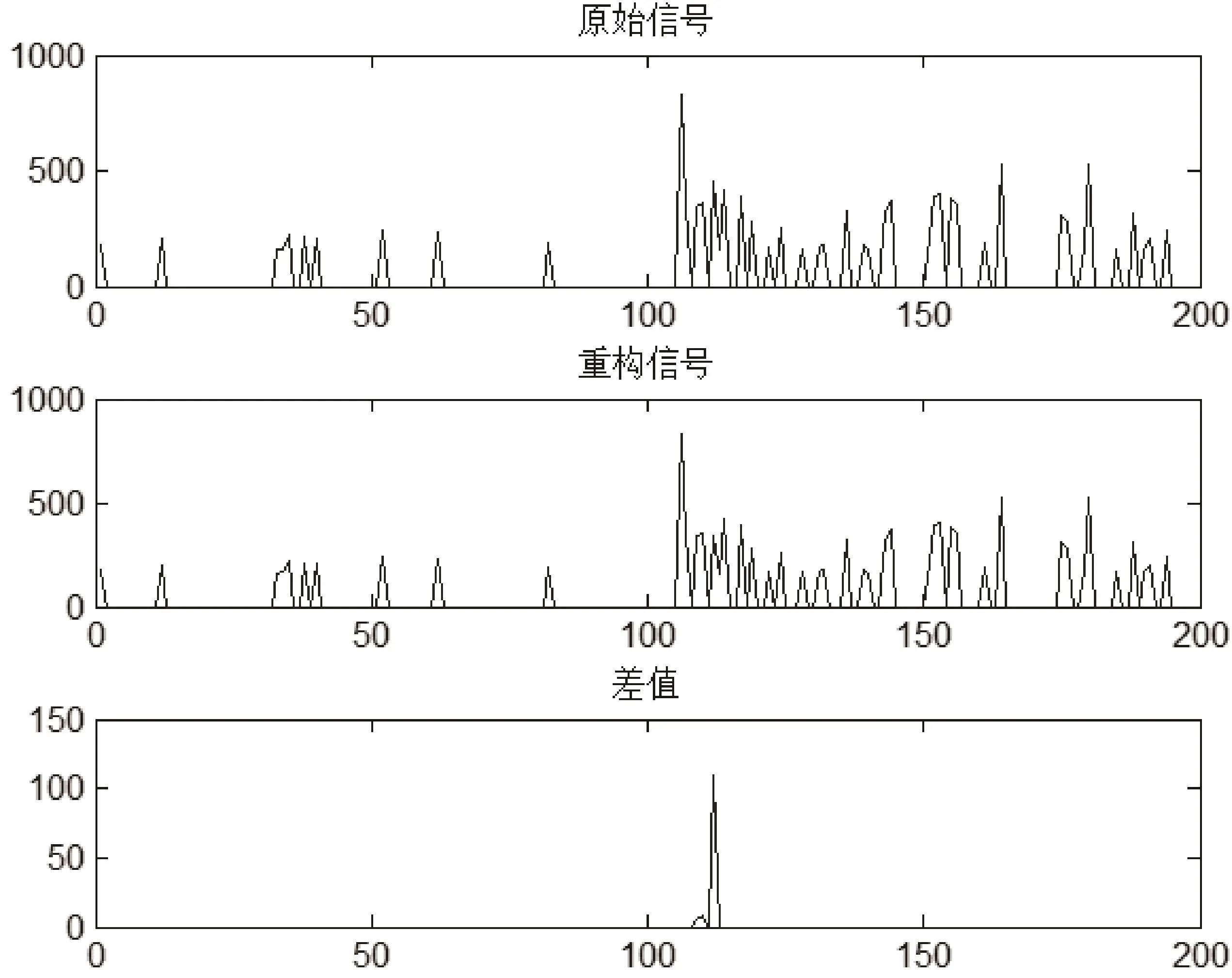
图3 n＝3时的数据重构结果

如图4所示，当n＝4时，原始数据共分为12个帧，信号压缩比为200：66，约为3.3：1。考虑通信中，每帧数据包需要额外增加两个字节原始帧长度和稀疏度信息，因此实际数据包长度压缩比率为156：400＝0.39。重建信号的精度为87%。

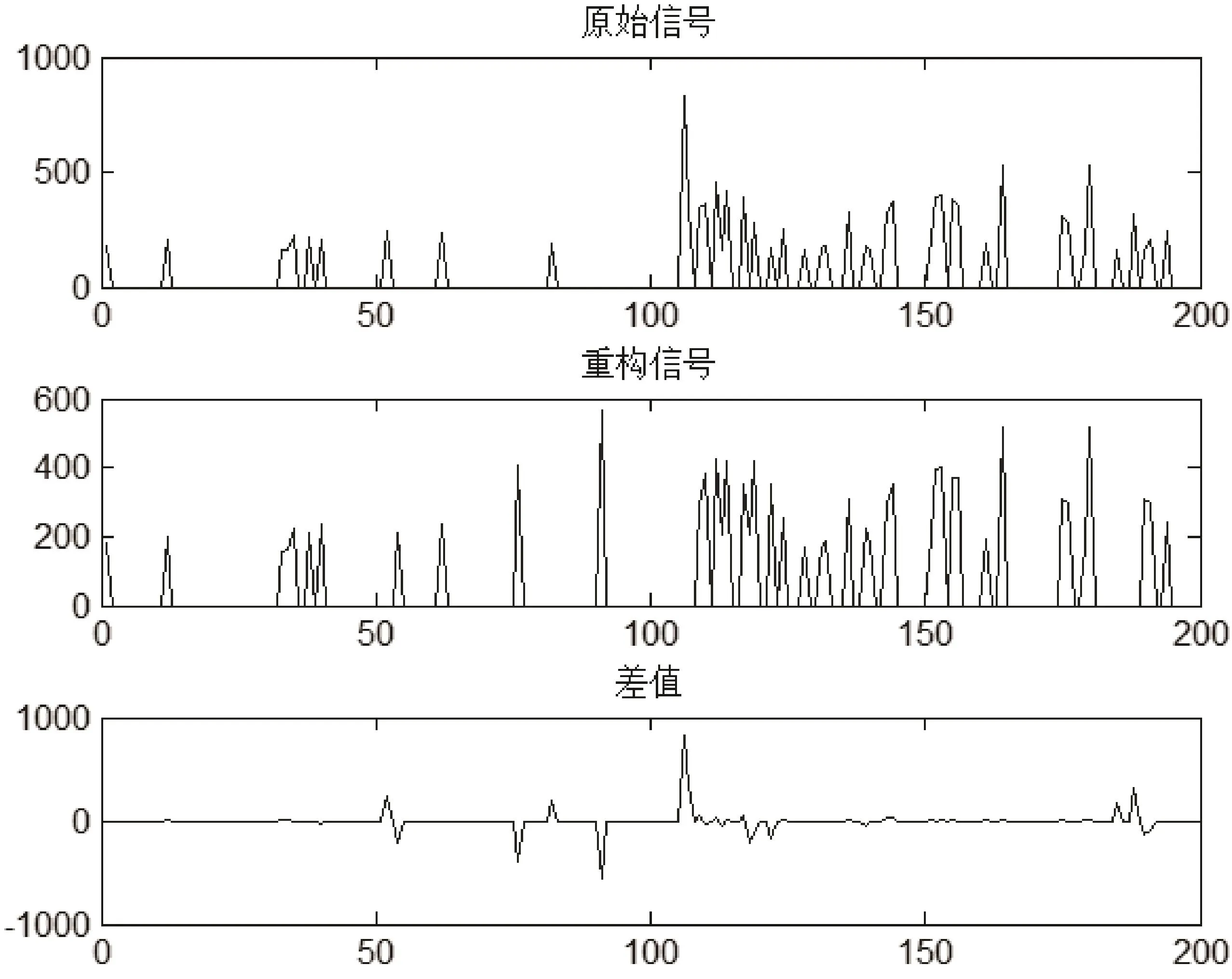
图4 n＝4时的数据重构结果

由上述实验结果可以看出，自适应条件下的数据重构精度较好，而且n越大恢复精度越低。从传输角度来看，n越大分帧数越少，产生的通信开销越少，n越小则重构概率越高、恢复精度越高。

4.2 不同稀疏度条件下实验结果分析

针对实验过程中采集的25组长度为200的数据进行压缩和重建，实验结果如图5所示。

图5 不同稀疏度条件下的试验结果

可以看出，Q-CSDR算法在各种稀疏度条件下均保持了较好的数据恢复精度，性能比较稳定。算法在较高稀疏度条件下也具有较好的恢复精度，但代价是增加了通信开销和数据压缩比：n＝2时的数据恢复精度最好，其压缩比和n＝3和n＝4时相差不多，其通信开销则高于后两种分帧方式。因此适用于对信号恢复精度要求很高、但对网络寿命要求较低的系统环境。n＝3时数据压缩比率最低，其通信开销小于n＝2，其数据精度则介于n＝3和n＝4之间，适用于对数据精度和网络寿命都有一定要求的系统环境。n＝4时，数据恢复精度较差，但其通信开销最小，适用于对数据精度要求不高，但对网络寿命要求较高的系统环境。此外，算法对稀疏度接近45的原始信号仍保持较高的重构概率，这也是由于减少了解空间数量，减少了估计信号的非零元素排列可能带来的影响。

4.3 同类算法对比分析

图6中显示的是在各稀疏度条件下，不同算法的性能对照（不考虑通信开销）。

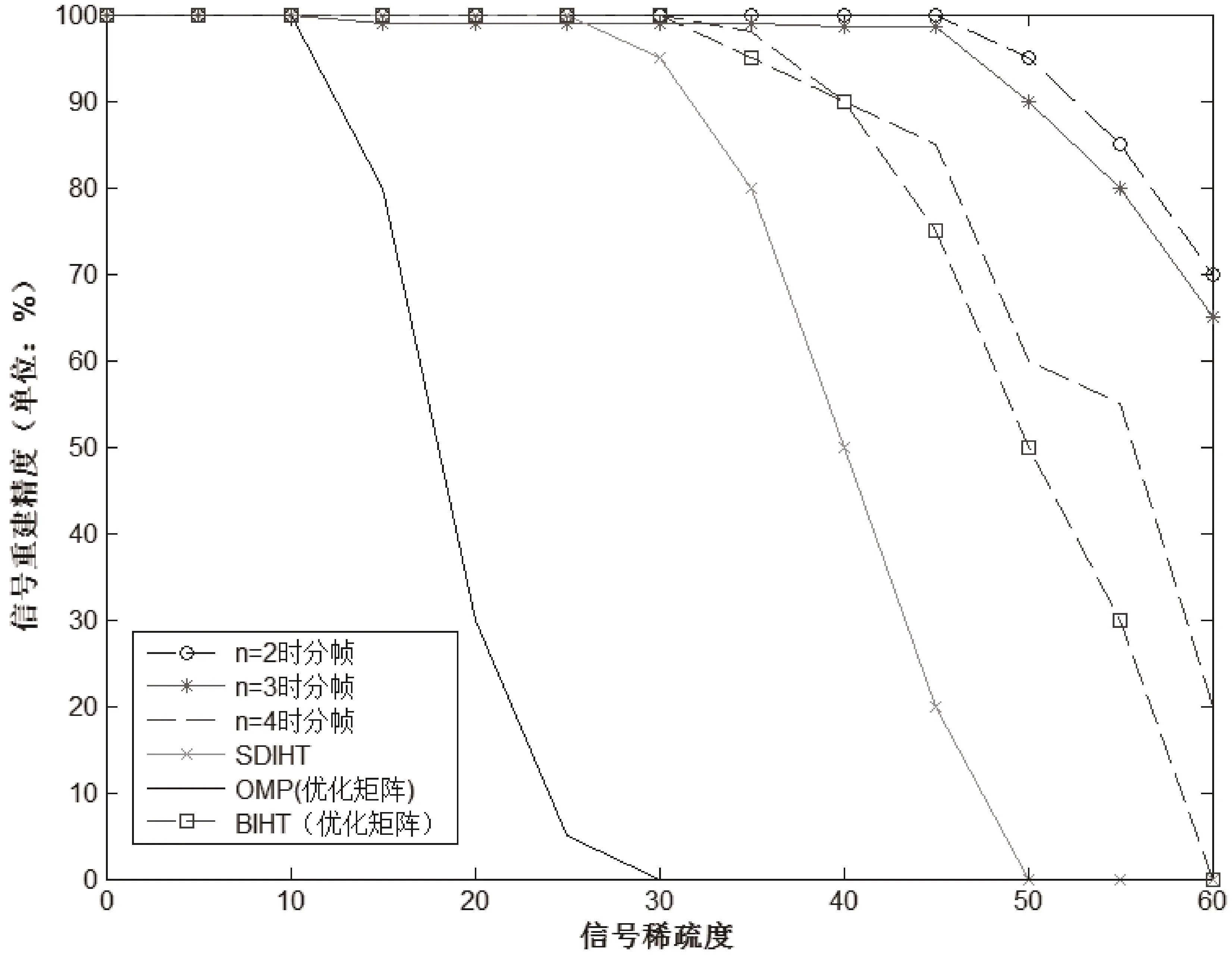
图6 同类算法实验结果对比

可以看出在稀疏度较小的条件下，各类算法都具有较好的数据恢复精度。而在稀疏度大于30后，OMP算法的数据恢复性能急剧下降，SDIHT及BIHT算法在稀疏度大于40后也出现了明显的下降趋势，而Q-CSDR算法在稀疏度大于45后出现明显下降，特别是n＝2时的Q-CSDR算法在稀疏度50时仍能保持90%的恢复概率，这也说明了分帧长度对于数据恢复精度的影响还是很明显的。

综上所述，Q-CSDR算法在稀疏度较大的前提下数据重构性能较其他几种算法好，但其缺点在于压缩时分帧长度无法预知，需要针对各个长度预设不同长度的观测矩阵，因此其观测矩阵字典需要的存储空间较多。从实验结果分析来看，n＝2时的通信开销较大，单从网络系统节能角度考虑并不是最优选择。因此在实际应用中采用了n＝3的QCSDR算法。

5 结束语

提出了基于量子免疫克隆的数据恢复算法。将量子免疫克隆与压缩感知数据恢复算法结合起来，在提高运算效率的前提下保证了数据恢复精度，并提出了自适应分帧方法。结果表明，算法能够在稀疏度较高的条件下精确的恢复出原始数据，并减小传输的数据量。本算法已经应用于秦始皇帝陵博物院野外文物安防系统中，经实际检验收到了良好效果，今后的工作将是如何降低数据恢复算法复杂度，减少观测矩阵的储存空间。

［1］Cands E，Romberg J，Tao T.Satable singal recovery form incomplete and inaccurate measurements［J］.Communications on Pure and Applied Mathematics，2006，59（8）：1207-1223.

［2］杨海蓉，张成，等.压缩传感理论与重构算法［J］.电子学报，2011，39（1）：142-148.

［3］Chen B S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，20（1）：33-61.

［4］Cands E J，Tao T.Decoding by linear programming［J］.IEEE Transactions on Information Theory，2005，51（12）：4203-4215.

［5］Tropp J A，Gilbert A C.Singal recovery from random measurements via orthogonal matching pursuit［J］.IEEE transactions on Information Theory，2007，52（12）：4655-4666.

［6］DaiW，Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction［J］.IEEE Transactions on Information Theory，2009，55（5）：2230-2249.

［7］Needell D，Tropp J A.CoSaMP：Iterative signal recovery form incomplete and inaccurate samples［J］.Applied and Computational Harmonic Analysis，2008，26（3）：301-321.

［8］Blumensath T，Davies M E.Iterative hard thresholding for compressed sensing［J］.Applied and Computational Harmonic Analysis，2009，27（3）：265-274.

［9］李佳，王强，沈毅，李波，等.压缩感知中测量矩阵与重建算法的协同构造［J］.电子学报，2013，41（1）：29-34.

［10］王娟.量子免疫克隆算法研究及在压缩感知重构中的应用［D］.南京：南京邮电大学，2012.

［11］朱丰，张群，柏又青，冯有前，张维强，等.一种新的基于遗传算法的压缩感知重构方法及其在SAR高分辨距离像重构中的应用［J］.控制与决策，2011，27（11）：1669-1675.

［12］Thong TDo，Gan Lu，Nguyen，Tran D.Sparsity adaptive matching pursuit algorithm for practical compressed sensing.Asilomar Conference on Signals，Systems and Computers［J］.Pacific Grove，California，2008（10）：581-587.

［13］刘亚新，赵瑞珍，胡绍海，姜春晖.用于压缩感知信号重建的正则化自适应匹配追踪算法［J］.电子与信息学报，2010，32（11）：2713-2717.

［14］Licheng Jiao，Yangyang Li.Quantum-inspired Immune Clonal Optimization［C］.Neural Networks and Brain，2005.ICNN＆B‘05.International Conference on.2005：461-466.

Algorithm of Com pressed Sensor Data Reconstruction Based on Quantum-inspired Immune Clon

QIHao1，LIU Zhou-zhou2
（1.School of Electronics and Information，Northwest Polytechnical University，Xi’an 710072，China；2.Xi’an Aeronautical University，Xi’an 710072，China）

An algorithm of compressed sensor data reconstruction，called Q-CSDR，based on the algorithm of quantum-inspired immune clon，is proposed in this paper.Q-CSDR can increase the probability of data reconstruction through framing the data adaptively.Because of its excellent performance，Q-CSDR uses the algorithm to accurately reconstruct the data.The experiment results show that，according to the sparsity of the original data，the algorithm can automatically adjust compression ratio，raise the accuracy of data reconstruction and adaptwell to high sparsity data reconstruction.It is used in the field security system of Emperor Qinshihuang｀smausoleum sitemuseum with good performance.

Quantum-inspired Immune Clonal Algorithm；Compressed Sensor；Data Reconstruction；Sparsity

10.3969／j.issn.1002-2279.2014.05.011

TP24

：A

：1002-2279（2014）05-0034-06

国家科技支撑计划（批准号：2010BAK67B09，2012BAK14B01）

祁浩（1982-），男，甘肃兰州人，博士研究生，主研方向：从事无线传感器网络、智能信息处理等方面的研究。

2014-06-11