高温气冷堆控制棒缓冲器的分析与试验验证

王少华，闫 贺，张作鹏，刁兴中

(清华大学 核能与新能源技术研究院 先进反应堆工程与安全教育部重点实验室，北京 100084)

控制棒薄壁壳缓冲器是安装在高温气冷堆堆芯石墨结构内的重要塑性变形吸能设备，用于缓冲驱动线断裂情况下产生的控制棒跌落冲击。高温气冷堆的控制棒运行在堆芯侧反射层的石墨孔道中，在极端事故情况下，假设控制棒驱动线断裂，由于仅存在氦气阻力，控制棒的下落近似于自由落体，当控制棒下落至孔道底部碰撞到底部的石墨时会具有很高的速度。为避免控制棒直接冲击堆内石墨构件造成破坏，必须在控制棒运行孔道底部石墨上设置一缓冲吸能装置，以保护堆内石墨结构。因此，需设计且实现一种可靠的、非能动的缓冲器，保证当控制棒驱动线断裂时底部的石墨不发生结构性破坏。该缓冲器需满足以下条件：1) 在满足使冲击力峰值尽可能小的同时，缓冲器必须能吸收最大可能的冲击动能，即当约200 kg的控制棒从8 m高处落下时的动能；2) 保证控制棒在与底部石墨发生碰撞后的回跳尽可能小，避免误引入正反应性；3) 保证控制棒缓冲过程的平稳连续，缓冲器能自适应控制棒的径向及角度偏差，不发生侧翻、倾倒；4) 保证在常温和高温(550 ℃)条件下缓冲器都能满足上述要求。

以上条件对控制棒缓冲器的设计提出了苛刻的要求，常见的非能动吸能结构包括金属薄壁壳[1]、复合材料薄壁壳[2]、泡沫金属[3]、蜂窝夹层结构[4]等。在反应堆工程中，须根据不同堆型的特点选择适当的控制棒缓冲器，如在FFR实验快堆中采用了变形套筒式后备减震器[5]、在水力驱动控制棒中采用了水力缓冲器[6]、在压水堆中曾采用弹簧式缓冲器[7]，综合考虑高温气冷堆的实际情况，选择薄壁金属壳方式是比较适合的。金属壳材料选择耐高温的奥氏体304不锈钢。金属壳的形状采用圆筒型式，这也是控制棒孔道的几何结构要求的，同时根据Jones[8]的总结，在截面面积相同的情况下，圆形截面的薄壁壳的吸能能力最高，渐进屈曲过程也最为稳定。

薄壁壳是一种常见的吸能结构，国外Alexander[9]、Ari-Gur等[10]及国内王仁等[11]对此问题进行了大量研究。HTR-10中也采用薄壁壳结构作为缓冲器，袁碧[12]对其缓冲效能进行了一系列的研究。但HTR-10的缓冲器结构，已不能满足缓冲200 kg的控制棒从8 m高处跌落的冲击，因此本文考虑实际工况，通过理论分析结合试验对缓冲器进行设计验证。

1 缓冲器设计

薄壁壳缓冲器结构如图1所示，其关键几何参数为薄壁壳的壁厚t、长度L、半径r。其中，承冲击环的作用是将冲击力均匀加载到薄壁壳，导向外筒用来限制薄壁壳的径向偏移，而缓冲器底板可将冲击力均匀地分散到底部的石墨。

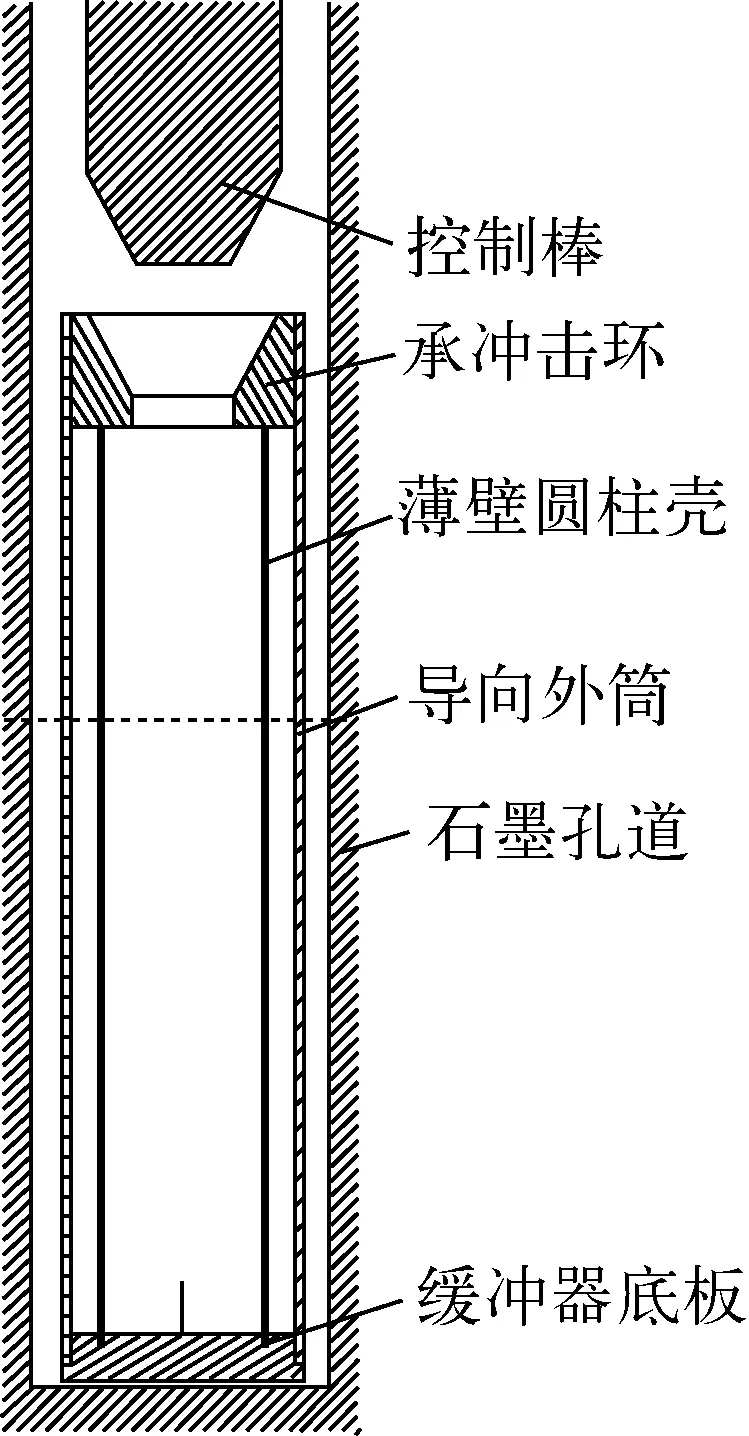
图1 薄壁壳缓冲器结构

在HTR-10的设计[12]中，并未将图1所示的薄壁壳的直径与长度作为重要的考虑因素。事实上，按照Singace等[13]的考虑偏心效应的圆柱壳能量吸收模型，薄壁壳的平均载荷Pavg和缓冲器能吸收的总能量Etotal可由以下公式计算：

(1)

Pavg/M0=22.27(2r/t)0.5+5.632

(2)

Etotal=ηPavgL

(3)

式中：M0为单位长度塑性极限弯矩；η为有效长度系数，工程上一般取0.75；σ0为304不锈钢的平均屈服应力，可用J-C本构模型[14]表示：

(4)

J-C本构模型中各参数的取值列于表1。

表1 J-C本构模型的参数

可看出，当吸收的总能量不变时，增加缓冲器的长度便能减小所需要的壁厚，同时减小了薄壁壳的峰值载荷和平均载荷，提高了整体的缓冲效果。但随高度/半径比值的增加，薄壁壳屈曲的稳定性会逐渐降低，当高径比达到一定数值时，会发生整体的欧拉压杆式失稳，缓冲器吸能效果急剧恶化，因此选择合适的半径和高度非常重要。

1.1 薄壁壳半径的选择

当薄壁壳发生屈曲时其水平截面的形状会发生变化，如图2所示。

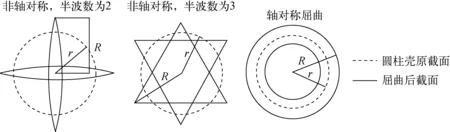
图2 薄壁壳屈曲后水平截面的形状

由图2可看出，当发生径向半波数为2的非轴对称屈曲时径向位移最大，若此时薄壁壳与导向外筒接触，外筒将会妨碍薄壁壳的屈曲且额外增加摩擦力，降低缓冲效果。假设半波数为2时薄壁壳的截面变成2条直线，直线长度为πr，可得出1个薄壁壳不同导向外筒内壁接触的充分条件：

r≤2R/π

(5)

图3 半波数为2的屈曲模态

式中：r为薄壁壳的半径；R为导向外筒的内径。通过式(5)可计算出薄壁壳的最大半径。实际上，薄壁壳不可能屈曲成直线，r≤0.7R的薄壁壳就能满足屈曲后不与导向外筒的内壁发生较强接触。利用ABAQUS模拟半波数为2的屈曲模态，屈曲后的外型如图3所示，此时薄壁壳屈曲后与圆心的最大距离为1.4r，表明半径r=0.7R的薄壁壳能满足设计需求。

1.2 薄壁壳长度的选择

薄壁壳整体是否发生欧拉失稳的临界长径比由多种因素决定，包括载荷的偏心程度、薄壁壳的材料、载荷的加载速度等，无法获得一理论解，只能利用试验验证。Hsu等[15]曾使用冲击锤对用304不锈钢制成的薄壁壳进行了冲击试验，根据其试验结果，当薄壁壳的L/2r达到6时开始出现整体失稳。根据此试验结果，可得到缓冲器的总长度L应满足的条件为L≤12r，考虑实际安装及试验条件本文选择L=11r。

1.3 薄壁壳壁厚的选择

图4 不同壁厚薄壁壳在各温度下的最大吸收能量

将L和r的具体数值代入式(1)～(3)，即可得到薄壁壳缓冲器所能吸收的最大能量与壁厚和温度的关系，如图4所示。

反应堆中控制棒总质量约200 kg，加上链条总质量约230 kg，最大跌落高度约为8 m，若不计阻力，控制棒所要吸收的最大能量Etotal=mgh，可得最大冲击能量为18 kJ，因此选择壁厚为2 mm的薄壁壳作为吸能体。

2 薄壁壳有限元模型的建立及分析

对所设计的薄壁壳缓冲器建立有限元模型，模拟分析控制棒以13 m/s速度冲击在薄壁壳上的动态过程。

真实的控制棒是由很多节短棒组成的一个整体，而每一节均有复杂的结构，包括中子吸收体、预紧弹簧、铰链等，是一类似于多节火车的结构，如图5所示。控制棒分为10节，在发生冲击前，每两节棒之间的可变间隙为2.5 mm，发生冲击过程中，最下面的1节棒首先冲击在薄壁壳上，此后9节棒会在很短时间内，逐一冲击在前一节棒上。理论上，逐节冲击的时间间隔仅为Δt=2.5/13 000=0.2 ms。当压缩波传至控制棒顶端时会反射回拉伸波，拉伸波不能直接穿过节与节之间的间断面，两节控制棒先是在拉伸波的作用下短暂分离，然后通过铰链传递拉伸波。同时应力波在包壳与中子吸收体之间也会有复杂的反射与透射现象，因此需对控制棒建立完整的有限元模型以进行计算。

图5 控制棒结构示意图及其中1节的有限元模型

基于ABAQUS/explicit平台建立有限元模型，控制棒整体采用C3D8R单元，网格采用结构化划分技术，铰链、石墨孔道和石墨下方的地面设置为刚体，弹簧简化为圆柱形弹性体，薄壁壳采用S4R单元，采用通用接触，接触属性设置为无摩擦。

分别计算从室温到600 ℃条件下缓冲器的吸能效果，图6为薄壁壳在常温下最终的屈曲模态，图7为缓冲器受到的最大冲击力以及缓冲器最终的压缩比与温度的变化关系。由图7可知，常温工况下缓冲器受到的冲击力最大，此时石墨表面受到的最大压应力为30 MPa，低于石墨的许用应力；600 ℃时缓冲器的压缩比最大，达到78%，仍在可接受范围内。

图6 常温下薄壁壳受冲击后的屈曲模态

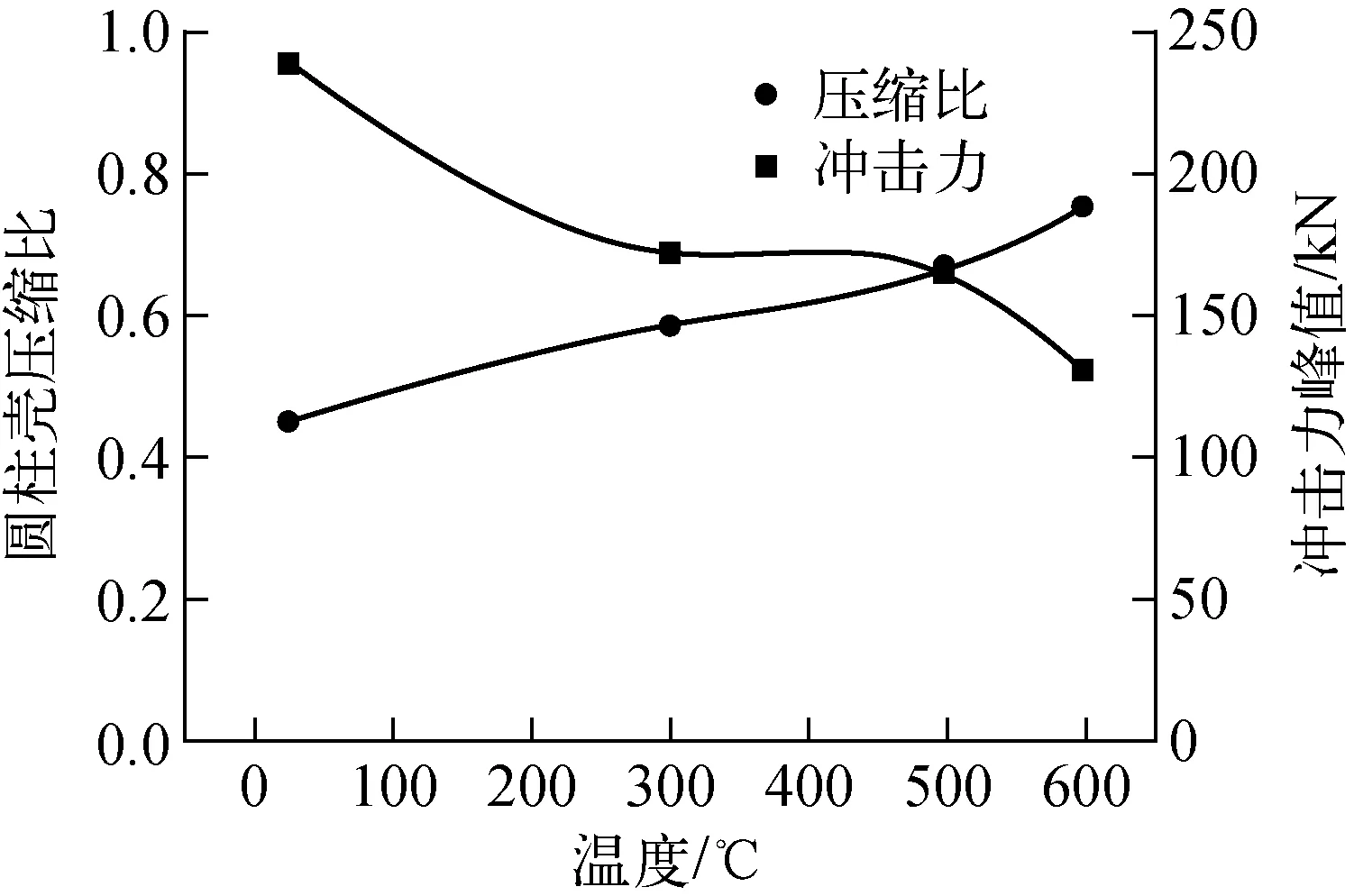
图7 不同温度下缓冲器的压缩比和峰值载荷

分析表明，设计的薄壁壳缓冲器能有效地吸收控制棒冲击的能量，保护石墨的安全。但通过计算还发现，两节控制棒之间的冲击力峰值为1 500 kN，控制棒包壳的最大应力为940 MPa，表明此时控制棒会发生一定的破坏。

3 试验设计

3.1 试验模型的简化

前文分析表明，控制棒在发生冲击后，薄壁壳能吸收控制棒的动能，避免损坏其底部的石墨结构，但控制棒在冲击过程中，存在较大的应力，会出现变形破坏，因此采用实际结构的控制棒进行多次冲击试验是不可行的。故在试验中采用一等重的单节实心棒模型进行冲击试验，考察薄壁壳缓冲器的缓冲效果。

图8为试验所用的等重钢棒结构与有限元模型。为研究等重单节棒的模型是否能有效代表和包络多节棒冲击的情形，首先对其建立有限元模型进行分析。图9为单根钢棒和真实的多节控制棒在常温下以相同的速度(13 m/s)撞击到缓冲器时，缓冲器底部的石墨受到的冲击力。可看出，多节棒产生的冲击力较单节棒多了很多高频振荡，反映出多节棒的冲击是一不连续的复杂过程；同时两者的峰值冲击力和平均冲击力大致相等，说明试验采用等重的单节钢棒模拟真实的多节棒是可行的，试验能验证薄壁壳缓冲器的可靠性。

图8 试验所用的单节棒结构和有限元模型

3.2 试验石墨块的选择

在真实的反应堆中缓冲器底部是石墨砖结构，试验中同样采用一石墨材料垫块模拟反应堆中的底部支撑。由于真实的石墨砖尺寸较大，因此有必要通过计算来分析试验采用何种尺寸的石墨块最为适合。以一半径60 mm、高200 mm的石墨圆柱为基础，通过不断加大石墨圆柱块的尺寸来观察控制棒跌落冲击对石墨块的作用，研究石墨表面冲击力随石墨尺寸变化的规律，进而推断采用何种尺寸的石墨块最适合模拟石墨砖及应变信号采集。

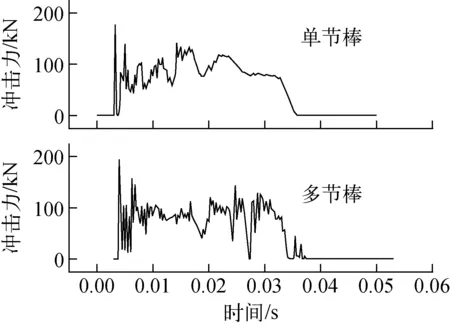
图9 试验所用的单节棒和多节棒的冲击力

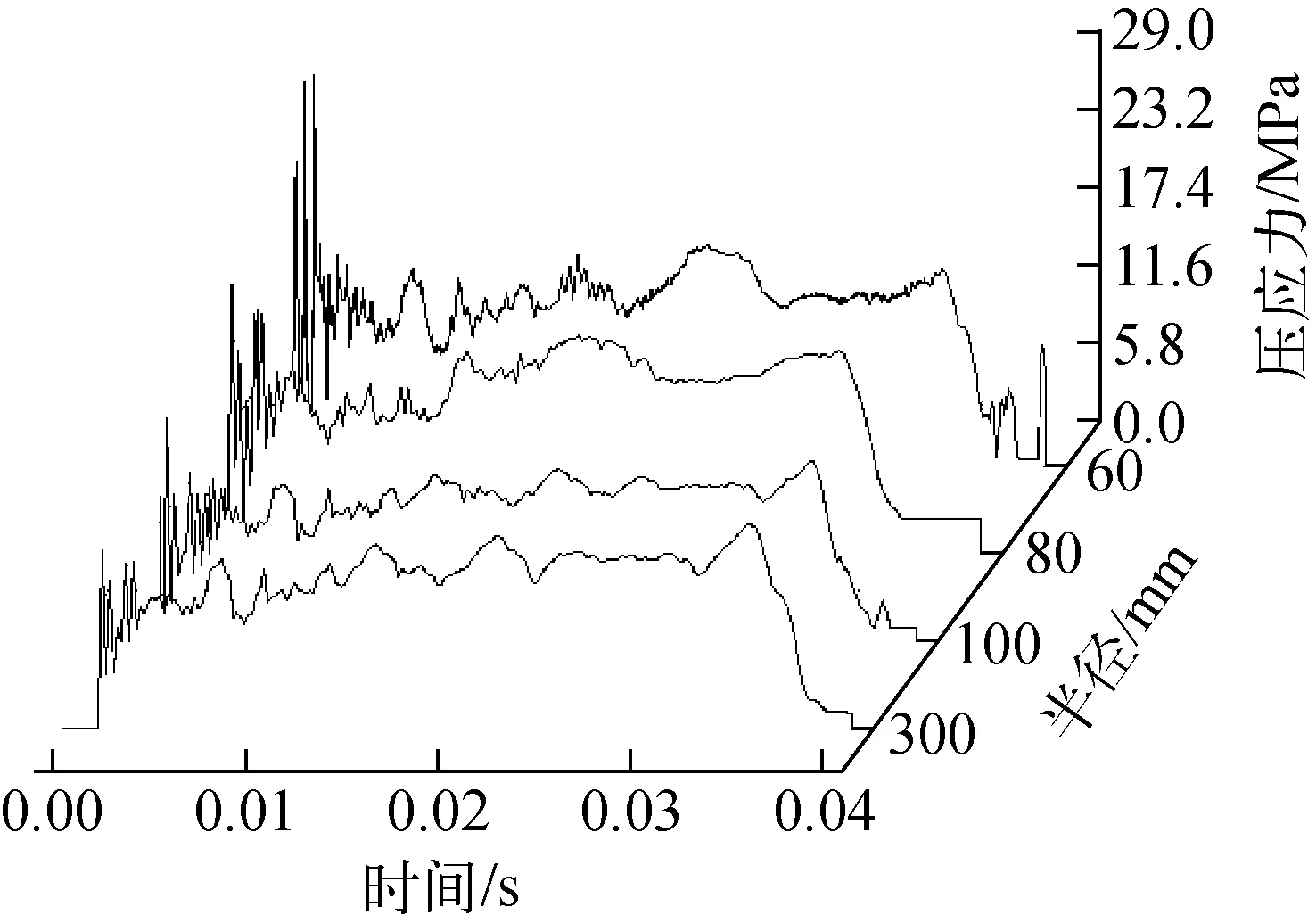
图10 石墨表面最大压应力随半径的变化

由于缓冲器底座半径为60 mm，以此为最小值，计算半径60、80、100、300 mm石墨受到冲击时的受力情况，石墨块的径高比保持为3/5。图10为石墨表面的最大压应力随半径的变化，可看出，当半径增加时最大压应力先是快速下降，当半径超过100 mm后基本保持不变且均小于石墨的抗压应力极限70 MPa。因此，选择半径为60 mm的石墨进行试验并以此判断缓冲器是否满足要求在工程上是最保守的，同时选择更大直径的石墨块也是适合的。

试验需通过测量石墨侧面的压应变间接测量冲击力的大小，图11为不同半径的石墨块侧表面的平均应变变化曲线。半径为60 mm的石墨侧面平均应变变化规律与表面最大压应力变化规律基本一致，但随半径的增加，不但平均应变的幅值迅速衰减，而且应变变化规律与冲击力的偏差也越来越大，当半径为300 mm时应变几乎是完全随机的，反映到曲线上便是其平均应变接近1条直线，即半径小的石墨块表面易出现应力最大值。综合这两方面考虑，试验选择60 mm半径的石墨块是最保守的。

图11 不同半径石墨块侧表面平均应变变化

3.3 试验台架设计

图12 试验台架示意图

为开展8 m控制棒跌落冲击试验，建立了一高14.4 m的试验台架，试验台架分为地上和地下两部分，台架结构如图12所示，地上3层钢结构台架总高7 m，地下2层台架总深7.4 m，提升机、控制棒落棒装置布置于台架的顶层，缓冲器、模拟石墨块和数据采集设备安装于台架最底层，控制棒的模拟孔道自下而上贯穿台架。

试验采用图8所示的长2.8 m、外径110 mm的均质钢棒作为模拟棒，在模拟棒底部加工出1个倒角与缓冲器顶部的承冲击环配合；缓冲器采用全尺寸模型，在缓冲器底部安放1个圆柱形石墨块来验证缓冲效果。石墨底部放有冲击力传感器，石墨侧面贴有应变片，以此来衡量冲击力的大小。

4 试验结果与分析

冲击试验后的石墨块和薄壁壳如图13所示，试验后石墨块保持结构完整，证明壁厚2 mm、材料为304不锈钢的薄壁壳能满足反应堆在冷态时的缓冲吸能的作用。同时屈曲后薄壁壳未与导向筒发生接触，薄壁壳发生了稳态的非轴对称屈曲，未发生整体欧拉失稳，与设计目标一致。

图13 试验结束后的薄壁壳和石墨块

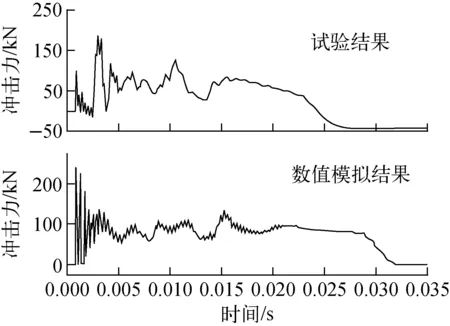
图14 试验得到的冲击力与数值模拟结果对比

图14为石墨所受整体冲击力试验值与数值模拟结果对比。可看出，因数值模拟中将地面模拟成刚体忽略了地面的吸能，导致数值模拟的冲击时间偏长。除此之外，数值模拟的石墨所受冲击力的大小与试验结果符合得很好，石墨所受到的最大冲击力约为200 kN。

5 结论

1) 相比HTR-10，提出缓冲器的直径和长度要优化地选择合适的值，以防壳体在屈曲过程中同导向筒接触，增加额外的冲击力，同时防止长度过长导致壳体发生整体欧拉失稳；经试验验证，所选择的半径和长度组合是合适的，屈曲后最大半径小于缓冲器导向外筒，同时屈曲模态为稳定的非轴对称渐进屈曲。

2) 模拟分析表明，设计的薄壁壳缓冲器能有效地完成吸能缓冲功能，保证石墨基底的完整性，石墨所受到的最大冲击力为200 kN，试验结果与模拟结果符合较好，互相验证了准确性。

3) 通过有限元计算，证明了在试验中采用单节等重钢棒代替多节的控制棒、采用小块石墨模拟整个石墨基底的近似是保守的，能包络代表实际工况。

参考文献：

[1] 杜星文，宋宏伟. 圆柱壳冲击动力学及耐撞性设计[M]. 北京：科学出版社，2004.

[2] CHING Q S, WAAS A M, HOFFMAN J, et al. The crushing response of braided and CSM glass reinforced composite tubes[J]. Composite Structures, 2001, 52(1): 103-112.

[3] CHEN W, WIERZBICKI T, BREUER O, et al. Torsional crushing of foam-filled thin-walled square columns[J]. International Journal of Mechanical Sciences, 2001, 43(10): 2 297-2 317.

[4] GOLDSMITH W, WANG G T, LI K, et al. Perforation of cellular sandwich plates[J]. International Journal of Impact Engineering, 1997, 19(5): 361-379.

[5] 杨志伸. FFR控制棒驱动机构样机的后备减振器[J]. 原子能科学技术，1991，25(5)：15-18.

YANG Zhishen. Design of the reserve damper in the FFR control rod drive mechanism prototype[J]. Atomic Energy Science and Technology, 1991, 25(5): 15-18(in Chinese).

[6] 宋威，秦本科，薄涵亮，等. 水力缓冲器三维流场数值分析[J]. 原子能科学技术，2013，47(5)：749-754.

SONG Wei, QIN Benke, BO Hanliang, et al. Numerical analysis of hydraulic absorber flow field[J]. Atomic Energy Science and Technology, 2013, 47(5): 749-754(in Chinese).

[7] 蒋贤国，胡俊，肖泽军，等. 反应堆控制棒驱动线缓冲试验研究[J]. 原子能科学技术，2007，41(增刊)：144-145.

JIANG Xianguo, HU Jun, XIAO Zejun, et al. Research on dashpot structure of rod cluster control assembly of reactor[J]. Atomic Energy Science and Technology, 2007, 41(Suppl.): 144-145(in Chinese).

[8] JONES N. Energy-absorbing effectiveness factor[J]. International Journal of Impact Engineering, 2010, 37(6): 754-765.

[9] ALEXANDER J M. An approximate analysis of the collapse of thin cylindrical shells under axial loading[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1960, 13(1): 10-15.

[10] ARI-GUR J, WELLER T, SINGER J. Experimental and theoretical studies of columns under axial impact[J]. International Journal of Solids and Structures, 1982, 18(7): 619-641.

[11] 王仁，韩铭宝，黄筑平，等. 受轴向冲击的圆柱壳塑性动力屈曲实验研究[J]. 力学学报，1983，19(5)：509-514.

WANG Ren, HAN Mingbao, HUANG Zhu-ping, et al. Dynamic plastic buckling of cylindrical shell under axial impact: An experimental study[J]. Acta Mechanica Sinica, 1983, 19(5): 509-514(in Chinese).

[12] 袁碧. HTR-10控制棒减震器设计的力学研究[R]. 北京：清华大学核能技术设计研究院，2001.

[13] SINGACE A A, ELSOBKY H, REDDY T Y. On the eccentricity factor in the progressive crushing of tubes[J]. International Journal of Solids and Structures, 1995, 32(24): 3 589-3 602.

[14] 魏延鹏. 304及316L不锈钢激光焊接件力学性能试验研究[R]. 北京：中国科学院力学研究所，2010.

[15] HSU S S, JONES N. Quasi-static and dynamic axial crushing of thin-walled circular stainless steel, mild steel and aluminum alloy tubes[J]. International Journal of Crashworthiness, 2004, 9(2): 195-217.