纵向涡发生器作用下矩形通道内流动换热性能研究

唐凌虹，谭思超，高璞珍

(哈尔滨工程大学 核安全与仿真技术国防重点学科实验室，黑龙江 哈尔滨 150001)

目前国际上在役和在研的反应堆中，板型元件是反应堆堆芯燃料元件的主要结构之一，这种结构中的冷却剂流道是一种横截面为窄间隙矩形半闭式长通道。纵向涡发生器(LVG)强化传热技术是基于纵向涡在流场中的流动特性来达到强化传热的目的。当流体流过一障碍物时，往往会在障碍物的背后空间产生系列漩涡，而这些漩涡的强烈运动，促进了主流区与传热壁面附近的流体间动量和能量的交换，强烈的扰动对边界层起减弱或破坏作用，因而使得传热增强。在矩形通道内布置纵向涡发生器对流动工质的传热性能进行强化得到很多学者的关注。王令等[1]、陈秋炀等[2]和Wang等[3]以核电站反应堆堆芯板状元件的强化传热为背景，采用实验的方法研究了水在带渐扩式纵向涡发生器的矩形通道内强化传热的特性，从实验结果来看，与光通道相比，阻力性能增加幅度(60%～70%)大于换热性能增强幅度(30%～55%)。而在纵向涡发生器翅管式换热器流动换热研究领域，却有了令人兴奋的研究成果，Torii等[4]对渐缩式纵向涡发生器翅管式换热器的流动换热性能进行了实验研究，实验结果指出：换热器管束以错排形式排列，相比较平直翅片，当Re从350增大至2 100时，纵向涡发生器换热性能增强30%～10%，而对应的阻力损失却减少55%～34%。Wu等[5]也实验研究了渐缩式纵向涡发生器的流动换热性能，他们指出，当换热器翅片侧空气最大流速为4.0 m/s时，纵向涡发生器的换热性能比平直翅片的增强16.5%，而阻力却几乎未增加。基于以上研究成果，本文对渐缩式纵向涡发生器与椭圆支柱(Case A)共同作用下矩形通道内的流动换热性能进行研究，并与渐缩式纵向涡发生器(Case B)和渐扩式纵向涡发生器(Case C)的流动换热性能进行对比，为反应堆堆芯板型元件冷却通道的热力设计提供参考。

1 物理模型及计算方法

本文所研究的纵向涡发生器矩形通道的几何模型如图1所示。水以速度u0从入口进入，流经一侧周期性纵向涡发生器的矩形通道后从出口流出。矩形通道尺寸为600 mm(D)×40 mm(W)×3 mm(H)，其中，通道进口段L1=100 mm，加热段L2=450 mm，出口段L3=50 mm[6]。其他几何参数列于表1。

在数值传热学中，描写流动与传热过程的3个基本方程为质量守恒方程、动量守恒方程和能量守恒方程，流动与换热控制方程的通用形式为：

·(ρ·

(1)

不同变量φ的扩散系数Γφ的具体形式详见文献[7]。

欲解决不同的问题，选择合适的紊流模型非常重要。紊流模型的权威Wilcox[8]在2001年发表的综述性论文中指出，对于k-ω模型、k-ξ模型、标准k-ε模型和RNGk-ε模型，在3种紊流情况下将实验和计算进行了比较，k-ω模型的精度最高。SST模型是在k-ω模型的基础上做了一定改进，应用由壁面到自由剪切层的过渡函数，更有利于处理边界层紊流到自由剪切紊流的过渡，因此本文采用FLUENT软件中的SSTk-ω湍流模型，对于固体壁面附近的黏性底层，流动与换热的计算采用低雷诺数k-ε模型，速度和压力的耦合问题采用SIMPLEC算法处理，对流项的离散格式为QUICK格式，扩散项采用中心差分格式(CD)。由于计算区域中同时存在着固体导热和流体对流换热，故采用流固耦合模型。采用GAMBIT生成结构化网格，在纵向涡发生器周围进行了局部加密，如图2所示。在计算之前对计算模型的网格无关性进行了考核，网格数量为284 420。

a——物理模型；b——Case A；c——Case B；d——Case C

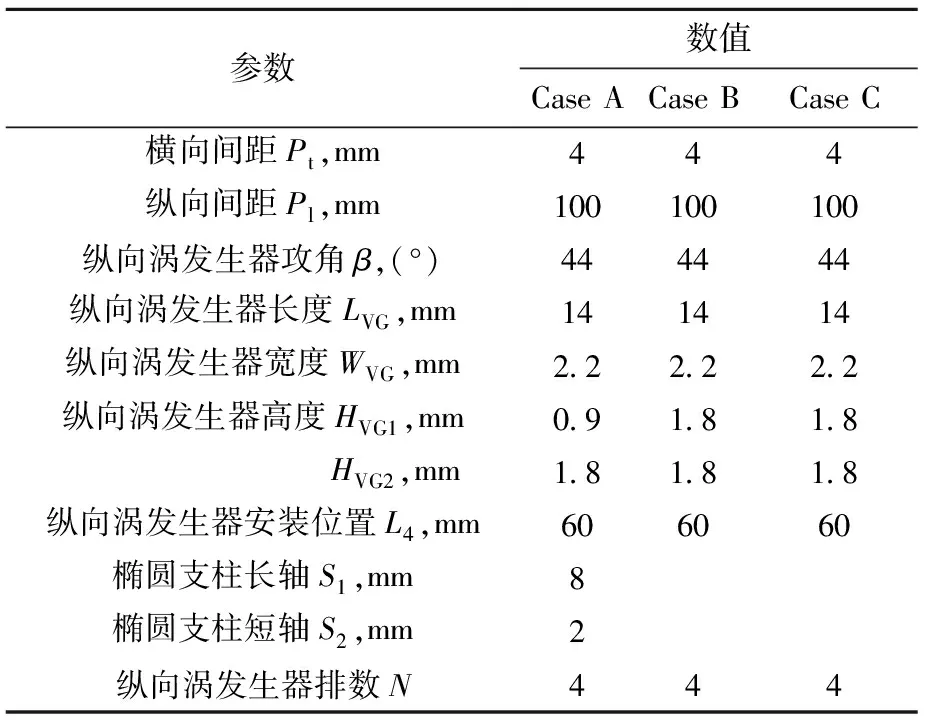
表1 不同纵向涡发生器几何参数

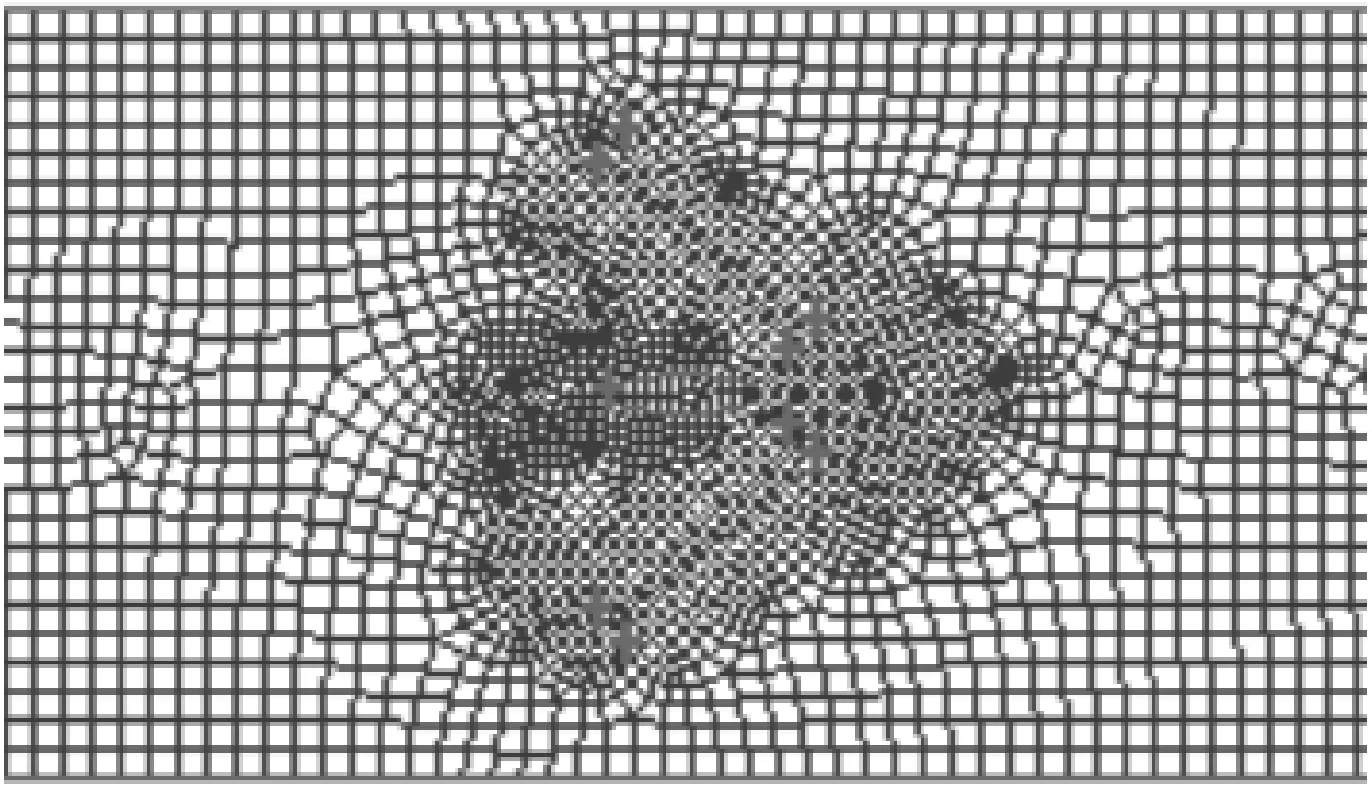
图2 纵向涡发生器周围计算网格

计算区域的各边界条件如下。进口边界：u=u0、v=w=0，温度300 K，压力0.1 MPa；出口边界：本文假定流体与换热均达到充分发展；固体壁面：矩形通道布置纵向涡发生器的表面为常热流边界条件，通道其余3个侧面均为绝热边界条件。

Reynolds数的定义为：

ReDh=u0Dh/ν

(2)

Nusselt数的定义为：

Nu=hDh/λ

(3)

j因子的定义为：

j=Nu/ReDhPr1/3

(4)

阻力系数f采用Darcy定义式：

(5)

式中：Dh为通道当量直径，Dh=4Ae/P，Ae为矩形通道的流通面积，P为湿周的周长；h为单位面积上平均换热系数，h=q/ΔT；L为流动方向总长度；Δp为矩形通道的流动阻力。

ΔT的定义为：

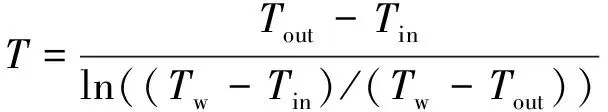
(6)

式中：Tin、Tout分别为矩形通道进、出口水的温度；Tw为加热板的平均壁面温度。

2 计算模型考核

在对矩形通道物理模型进行数值计算前，本文采用文献[6]的实验数据对计算模型的可靠性进行了考核。文献[6]对渐扩式纵向涡发生器(Case C)作用下的窄矩形通道在单相水条件下的流动传热性能进行了实验，获得了流动传热性能的实验数据。图3示出了计算结果与实验结果的比较，Nu的最大相对偏差为7.3%，平均相对偏差为6.0%；f因子的最大相对偏差为-7.0%，平均相对偏差为-2.9%，可认为纵向涡发生器计算模型是可靠的。

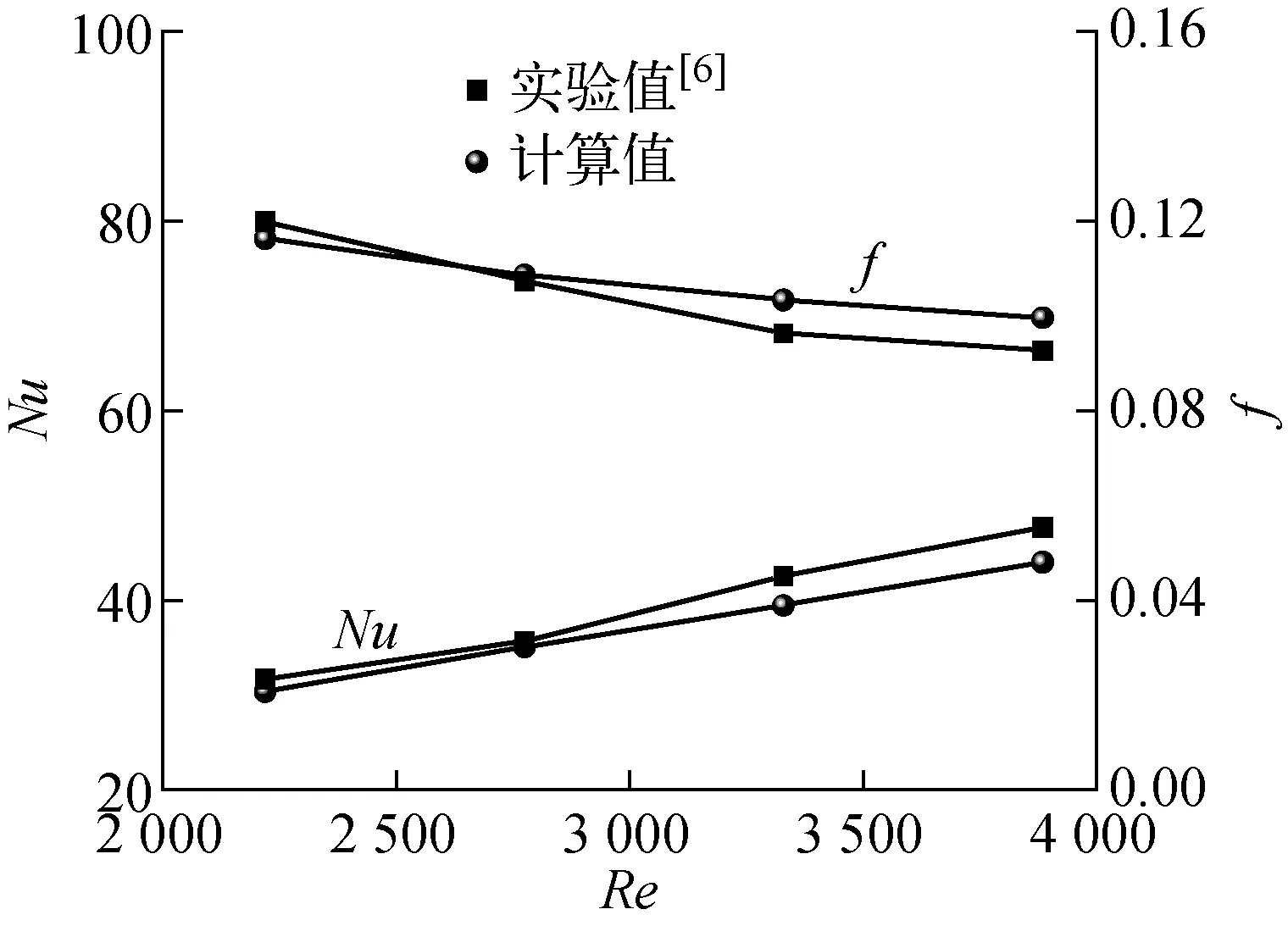
图3 Case C计算值与实验值对比

3 三种形式纵向涡发生器流动换热性能比较

3.1 换热性能比较

不同矩形通道内换热性能比较如图4所示。由图4可知，随矩形通道内Re的增大，矩形通道内换热性能均得到增强；在相同Re下，Case B的Nu最大，光通道的Nu最小，在Re计算范围内，Case A、Case B和Case C换热性能分别较光通道的增强了17.5%～21.4%、18.9%～23.2%和16.8%～20.7%。

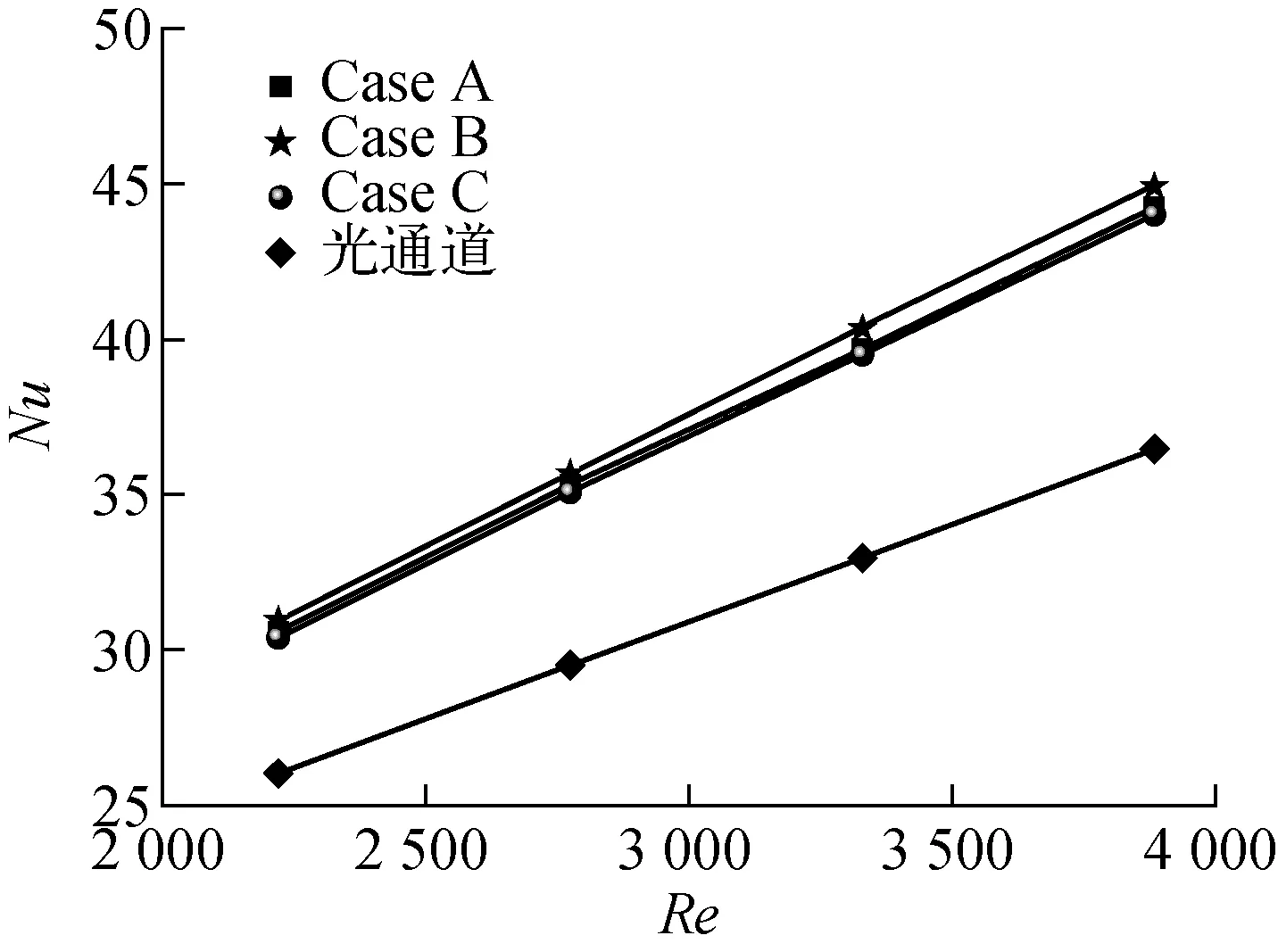
图4 不同布置方式矩形通道换热性能比较

为详细了解纵向涡发生器对矩形通道内流动换热性能的影响，本文选取第1排纵向涡发生器前后4个截面对比不同通道内的速度场，图5示出入口速度u0为0.6 m/s时不同矩形通道x方向截面的速度分布。从图5可看出，由于纵向涡发生器的作用流体产生了强烈的漩涡，对于光通道，垂直流动主流方向的截面上速度很小，在加装纵向涡发生器后，相应截面上的速度增大较多，这可使截面内流动工质的换热增强，有利于降低加热板的表面温度，最终可提高反应堆堆芯的CHF值。

场协同原理是从温度场与速度场之间的关系来揭示对流换热的机理。场协同理论指出在流动换热过程中，速度与温度梯度之间的协同越好，在其他条件相同的情况下，换热就越强烈[9]。本文利用场协同原理对不同矩形通道内流动换热机理进行探讨。协同角采用全场体积平均角来计算[10]：

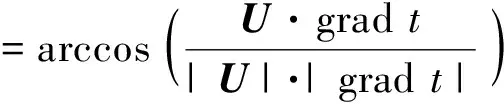
(7)

(8)

图6为不同布置方式矩形通道平均协同角比较。可看出，不同矩形通道内的平均协同角随Re的增加而增大，在相同Re下，纵向涡发生器作用下矩形通道的平均协同角均比光通道的小，表明纵向涡发生器降低了通道内速度与温度梯度之间的夹角，因此强化了对流换热，这从机理上揭示了纵向涡发生器能强化对流换热的原因。在3种纵向涡发生器中，Case B的平均协同角最小，表明Case B产生的纵向涡更有利于改善矩形通道内温度场与速度场的协同性，使通道的换热性能增强。

3.2 阻力性能比较

图7为4种矩形通道内阻力性能的比较。值得注意的是，Case A的f因子明显小于Case B和Case C的f因子，在Re计算范围内，Case A的f因子分别较Case B和Case C的减小了18.2%～23.0%和17.7%～21.3%。这表明在获得相同的流量时，布置Case A的矩形通道所消耗的泵功要明显小于Case B和Case C。图8示出入口速度u0为0.6 m/s时3种纵向涡发生器作用下矩形通道内局部阻力损失的比较。从图8可看出，当水流到纵向涡发生器之前，矩形通道内的局部阻力损失几乎相同，当水流过纵向涡发生器过程中，Case C的局部阻力损失最大，Case A的局部阻力损失最小，这样就导致在整个流动长度上，Case C的流动阻力最大，Case A的流动阻力最小。这种现象可解释如下：Case A纵向涡发生器翼形为梯形，梯形的前缘对矩形通道充分发展的流体的阻碍作用减小；同时纵向涡发生器与椭圆支柱形成的类似喷嘴状流道促进了水流加速运动，延迟了流动边界层的分离，同样减少了纵向涡发生器的形阻，从而使流动阻力减小，文献[4-5]的研究也得出了相似的结论。

a——Case A；b——Case B；c——Case C；d——光通道

图6 不同布置方式矩形通道平均协同角比较

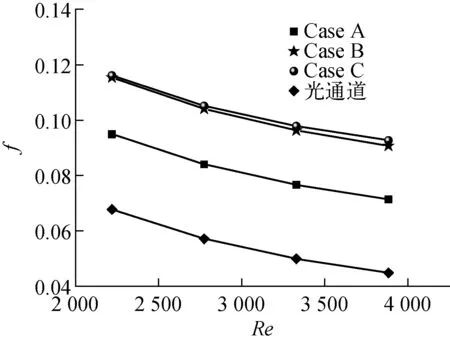
图7 各矩形通道阻力性能比较

图8 3种纵向涡发生器局部阻力损失比较

3.3 矩形通道综合性能比较

从上述比较可知，在相同Re下，Case B的换热性能最好，光通道的阻力损失最小，本文采用JF因子对各矩形通道的综合流动换热性能进行比较。JF因子定义[11]如下：

(9)

式中，下标“ref”表示光通道。

图9为各通道JF因子随Re的变化情况。在Re计算范围内，Case B和Case C的JF因子均小于1，表明两者的综合流动换热性能低于光通道，而Case A的JF因子大于1，其综合性能优于光通道，即Case A能以较小的阻力代价得到较大的换热效果，是一种理想的强化换热方式。

图9 各矩形通道JF因子比较

4 结论

本文对布置3种不同形式纵向涡发生器矩形通道和光通道的流动换热性能进行了比较，主要结论如下。

1) 在相同Re下，Case B的Nu最大，光通道的Nu最小，在Re计算范围内，Case A、Case B和Case C换热性能分别较光通道增强了17.5%～21.4%、18.9%～23.2%和16.8%～20.7%。

2) 在相同Re下，纵向涡发生器作用下矩形通道的平均协同角均比光通道的小。在3种纵向涡发生器中，Case B的平均协同角最小，表明Case B产生的纵向涡更有利于改善矩形通道内温度场与速度场的协同性，使通道的换热性能增强。

3) Case A的f因子明显小于Case B和Case C的，在Re计算范围内，Case A的f因子分别比Case B和Case C的减小了18.2%～23.0%和17.7%～21.3%。

4) 在Re计算范围内，Case B和Case C的JF因子均小于1，而Case A的JF因子大于1，表明Case A能以较小的阻力代价得到较大的换热效果，是一种理想的强化换热方式。

参考文献：

[1] 王令，陈秋炀，曾敏，等. 矩形窄通道内带纵向涡发生器的传热强化试验研究[J]. 化工学报，2006，57(11)：2 549-2 553.

WANG Ling, CHEN Qiuyang, ZENG Min, et al. Heat transfer enhancement in rectangular narrow channel with longitudinal vortex generators[J]. Journal of Chemical Industry and Engineering, 2006, 57(11): 2 549-2 553(in Chinese).

[2] 陈秋炀，曾敏，王令，等. 纵向涡发生器对矩形窄通道内对流换热的影响[J]. 西安交通大学学报，2006，40(9)：1 010-1 013.

CHEN Qiuyang, ZENG Min, WANG Ling, et al. Effect of longitudinal vortex generators on convective heat transfer in rectangular narrow channel[J]. Journal of Xi’an Jiaotong University, 2006, 40(9): 1 010-1 013(in Chinese).

[3] WANG Q W, CHEN Q Y, WANG L, et al. Experimental study of heat transfer enhancement in narrow rectangular channel with longitudinal vortex generators[J]. Nuclear Engineering and Design, 2007, 237: 686-693.

[4] TORII K, KWAK K M, NISHINO K. Heat transfer enhancement accompanying pressure-loss reduction with winglet-type vortex generators for fin-tube heat exchangers[J]. International Journal of Heat and Mass Transfer, 2002, 45: 3 795-3 801.

[5] WU J M, ZHANG H, YAN C H, et al. Experimental study on the performance of a novel fin-tube air heat exchanger with punched longitudinal vortex generator[J]. Energy Conversion and Management, 2012, 57: 42-48.

[6] 黄军. 纵向涡作用下窄间隙矩形通道内单相和沸腾流动传热特性机理研究[D]. 西安：西安交通大学，2009.

[7] VERSTEEG H K, MALALASEKERA W. An introduction to computational fluid dynamics: The finite volume method[M]. New York: Prentice-Hall, 1995.

[8] WILCOX D C. Turbulence modeling: An overview[C]∥39th Aerospace Sciences Meeting & Exhibit. Reno, Nevada, USA: AIAA, 2001.

[9] GUO Z Y, LI D Y, WANG B X. A novel concept for convective heat transfer enhancement[J]. International Journal of Heat and Mass Transfer, 1998, 41: 2 221-2 225.

[10] WU J M, TAO W Q. Numerical study on laminar convection heat transfer in a rectangular channel with longitudinal vortex generator, Part A: Verification of field synergy principle[J]. International Journal of Heat and Mass Transfer, 2008, 51: 1 179-1 191.

[11] YUN J Y, LEE K S. Influence of design parameters on the heat transfer and flow friction characteristics of the heat transfer with slit fins[J]. International Journal of Heat and Mass Transfer, 2000, 43: 2 529-2 539.