一种多输入多输出雷达相位编码信号的设计方法

杜晓林,苏涛,朱文涛,张龙

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

一种多输入多输出雷达相位编码信号的设计方法

杜晓林,苏涛,朱文涛,张龙

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

针对多输入多输出(MIMO)雷达正交相位编码信号设计中已有方法所得信号集匹配滤波后旁瓣较高的问题,提出一种新的设计方法。首先将基于信号集相关旁瓣总能量的代价函数简化成低次的较容易求解的问题,然后将输入输出算法从一维扩展到多维,并针对极小化问题改进了其物面和频谱面的约束条件,利用改进后的输入输出算法求解该极小化问题,再针对基于信号集相关旁瓣峰值的代价函数,利用迭代码选择算法对第一步所得信号集进一步优化,最后得到相关性能较好的正交信号集。仿真结果表明,相比于模拟退火和序列二次规划等方法,该方法所得信号集的平均非周期自相关峰值旁瓣降低了3～4 dB,平均非周期互相关峰值降低了1～2 dB。

雷达;多输入多输出;迭代码选择算法;相位编码

多输入多输出(MIMO)雷达具有多个发射天线和接收天线,按照天线之间距离的远近,通常将MIMO雷达分为分布式和集中式2类。分布式MIMO雷达的天线间距较大,具有空间分集增益,使雷达可以从不同角度对目标进行观测,从而对抗目标的闪烁效应,提高探测能力;集中式MIMO雷达的天线间距较小,多个收发天线到目标的射线近似平行,而且各目标相对于收发天线有相同的波达方向,每个天线可以发射任意信号,容易实现灵活的发射分集设计,相比传统的相控阵雷达,集中式MIMO雷达能够提供更多的系统自由度以及更大的阵列孔径,具有更高的分辨率,更好的参数识别能力,而且能够进行灵活的方向图设计和波形集优化[1-4]。

为了抑制不同目标回波之间的干扰并获得对多个目标的高分辨率,MIMO雷达一般采用正交相位编码信号集作为发射信号。文献[5-9]均以最小化信号集相关旁瓣总能量作为准则(本文将文献[6]和文献[9]的代价函数归为最小化相关旁瓣总能量准则)设计了正交相位编码信号集。其中文献[5-6]分别采用混合模拟退火和混合遗传算法作为设计方法,所得信号集的相关旁瓣较低。文献[7]采用加权循环算法设计出积分旁瓣电平(integrated sidelobe level, ISL)较低的恒模序列,并且具有计算存储量较小,设计速度快等优点。文献[8]采用互熵方法,通过对序列施加一个谐波相关的结构约束,设计了具有一定多普勒容忍性的正交相位编码信号集。文献[9]利用改进的Flethcher-Reeves算法,不施加约束条件,设计了一组具有低相关旁瓣的信号集。但是,文献[5-9]中所得信号集的非周期自相关旁瓣峰值(autocorrelation sidelobe peak, ASP,记为u)和非周期互相关峰值(crosscorrelation peak, CP,记为v)仍然较高。

针对MIMO雷达正交相位编码信号设计中,传统方法所得信号集的相关旁瓣较高的问题,本文将输入输出算法[10-14]应用于MIMO雷达相位编码信号设计中,提出一种混合输入输出算法,该算法由改进的输入输出算法和迭代码选择算法[15]2个步骤组成。首先将基于信号集相关旁瓣总能量的代价函数化简成低次的较容易求解的问题,然后将输入输出算法从一维扩展到多维,并针对极小化问题改进了其物面和频谱面的约束条件,利用改进后的输入输出算法求解该极小化问题。再针对基于信号集相关旁瓣峰值的代价函数,利用迭代码选择算法对第一步所得信号集进一步优化,最后得到相关性能较好的正交信号集。

1 问题描述

考虑一个具有M个发射阵元的MIMO雷达,各阵元发射相位编码信号,发射信号的子脉冲个数为N,则发射信号集为

S=[s1,s2,…,sM]N×M=[y1,y2,…,yN]T

(1)

式中:sm=[sm(1),sm(2),…,sm(N)]T为第m个阵元发射的相位编码信号;yn=[s1(n),s2(n),…,sM(n)]T代表全部M个阵元在第n个时刻的码元,且sm(n)=ejφm(n)(0≤φm(n)≤2π)。

信号sm1(n)和sm2(n)的相关函数为

m1,m2=1,…,M;k=0,…,N-1

(2)

式中:当m1=m2时,rm1m1(k)为sm1(n)的非周期自相关函数;当m1≠m2时,rm1m2(k)为sm1(n)和sm2(n)的非周期互相关函数;(·)*表示复共轭计算[5-9]。

由信号的相关函数可得发射信号集相关矩阵为

(3)

由式(2)给出M个自相关函数旁瓣峰值u和M(M-1)/2个互相关函数峰值v的定义分别为[5-9,16-18]

(4)

v=max|(rm1,m2(n))/N|,m1≠m2,

m1,m2=1,…,M

(5)

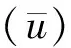
在给出了评价指标的定义之后,本文要解决的问题就是通过某种极小化准则来设计平均ASP和平均CP较低的正交相位编码信号集。考虑到相关旁瓣总能量的降低会使相关旁瓣峰值稳定地降低[5],因此建立基于信号集相关旁瓣总能量的代价函数E1[5-9]和基于信号集相关旁瓣峰值的代价函数E2分别为

(6)

式中:‖‖表示矩阵的F范数(如无特别说明,矩阵范数均为F范数,而向量范数均为欧式范数)。

(7)

为得到正交相位编码信号集,本文利用混合输入输出算法求解代价函数式(6)和式(7)。

2 正交相位编码信号的设计

混合输入输出算法包括2个步骤:①针对代价函数E1,利用改进的输入输出算法求解,并把这一步所得信号集作为第2步的初始输入值;②针对代价函数E2,利用迭代码选择算法求解。下文首先将代价函数E1转化为适合求解的极小化问题,然后概述输入输出算法的基本原理,进而说明改进的输入输出算法的具体求解步骤,最后叙述迭代码选择算法的算法流程。

2.1 改进的输入输出算法求解代价函数E1

2.1.1 代价函数E1的转化 因为E1是关于自变量S的4次函数,为了降低求解的复杂度,本文首先对代价函数进行转化。

由式(3)中Rn的定义,可得yn的谱密度矩阵为

(8)

根据帕斯瓦尔定理得

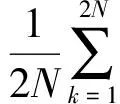
(9)

(10)

由于M-1是E1的下界[7],而M确定为常数,因此代价函数E1可以转化为如下极小化问题

s.t. |sm(n)|=1;m=1,…,M;n=1,…,N

‖ak‖2=1;k=1,…,2N

(11)

可以看出,借助M×1维的辅助变量ak,E1化简为自变量S的2次函数。

为了求解式(11)中的极小化问题,定义离散傅里叶变换(discrete Fourier transform, DFT)的正交矩阵D为

(12)

(13)

2.1.2 代价函数E1的求解 本文利用改进的输入输出算法对代价函数E1进行求解。由于输入输出算法是在Gerchberg-Saxton(GS)算法[12-14]的基础上发展而来,所以先简单描述GS算法的基本原理。

GS算法是一种数据点迭代傅里叶变换的相位恢复算法,其基本原理是固定输入面和输出面的振幅分布,利用2个平面上的傅里叶变换(FFT)和逆傅里叶变换(IFFT)交替迭代计算,恢复输入平面的相位。具体过程为:

(1)先任意给定一个输入面上的初始相位分布φ,然后将相位φ与入射光振幅|f(x)|构成入射波函数f(x),对f(x)进行傅里叶变换得F(u);

(2)用F(u)的相位部分与输出平面上的振幅函数|F(u)′|构成复函数F(u)′;

(3)对F(u)′作逆傅里叶变换得复函数f(x)′;

(4)取f(x)′的相位部分与预定输入光振幅|f(x)|构成新的波函数作为下一次迭代的输入信息。

执行上述迭代步骤,若迭代后的结果满足收敛条件,则迭代过程结束,若不满足,则继续执行下一次迭代。随着迭代次数的增加,输出的图像会逐渐收敛为具有预定振幅的图像,而所要恢复的相位即为输入面上最终所得的相位φ。

为了提高GS算法的性能,Fienup等人将其修改为输入输出算法[10]。输入输出算法的前3步和GS算法相同,区别在于第4步增加了空间域限制,即

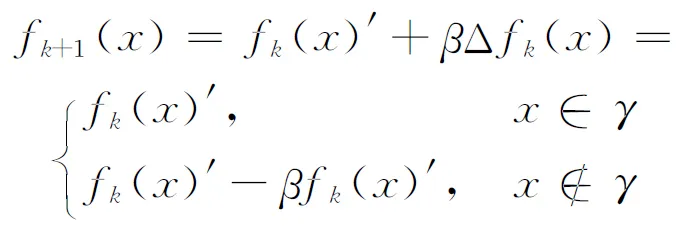
(14)

式中:γ是满足约束条件的点集;β为常数。文献[10]已经证明,相比GS算法,输入输出算法的收敛速度更快。

MIMO雷达相位编码信号设计的目的是为了获得一组恒模的相位编码信号集,由式(13)可得代价函数由时域(S′)和频域(Q)2部分构成,恒模即时域信号的幅度固定为1,频域信号的幅度也可以修改为满足一定的约束条件,即应用GS算法和输入输出算法的前提是具备的。因为利用时域和频域交替傅里叶变换对式(13)极小化的过程与相位恢复中恢复输入平面相位的过程是一致的,所以GS算法和输入输出算法适合对本文问题进行求解。

GS算法和输入输出算法的流程图分别如图1和图2所示[10-14]。

图1 GS算法的流程图

图2 输入输出算法的流程图

输入输出算法是对数据点的一维迭代傅里叶变换,而式(11)中的自变量是多维,因此首先将输入输出算法扩展到多维,然后根据极小化问题中的约束条件将算法中2个平面的约束条件进行改进,从而使改进后的输入输出算法适合求解本文中的极小化问题。

利用在[0,2π]内均匀分布的随机相位对S进行初始化,在随后的每次迭代,该信号集将被算法步骤(4)中所得的新信号集取代。

改进的输入输出算法步骤如下。

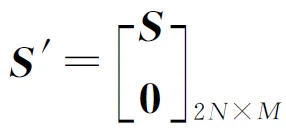
(15)

将归一化后的DFT通道系数记为ak(m),m=1,…,M,则有下式成立

k=1,…,2N

(16)

与输入输出算法中的频谱面幅度代入操作不同,此处的约束条件修改为所有DFT通道系数的平方和等于1,这同时也使式(11)中的约束条件‖ak‖2=1成立,改进后的约束条件更适于本文中对极小化问题的求解。

(4)改进物面的幅度约束,并进行空间域限制。物面的幅度约束可以表示为

(17)

式中:exp(jarg(S′))用来约束每个信号的模值为1,这也使式(11)中的约束条件|sm(n)|=1成立;β的取值在0.5到1之间,当β=1时,不满足空间域限制的点集的相位置0。

执行迭代步骤(1)～(4),直到相邻2次迭代所得信号集之间的误差满足如下条件

‖S(i)-S(i+1)‖<ε

(18)

式中:S(i)表示第i次迭代中所得信号集矩阵;ε为预先设定的较小值,如10-4。

图3给出了改进的输入输出算法的流程。

图3 改进的输入输出算法流程图

2.2 迭代码选择算法求解代价函数E2

迭代码选择算法最早用于获得具有较好非周期相关性的二进制序列[15],本文将其作为混合输入输出算法的第2步,来设计相位取值连续的正交相位编码信号集。

将第1步所得优化结果作为第2步的信号集初始输入,利用[0,2π]内均匀分布的随机相位逐个替代初始输入信号集中的相位φm(n),并且计算新信号集的代价函数,如果由于相位的替代使得代价函数E2减小,则接受改变后的相位,否则保留原来的相位。信号集的每一个相位都进行上述相位替代操作,直到相位变化标志符为0,即没有新的相位被接受,此时第2步的优化过程结束。迭代码选择算法的流程如图4所示。

图4 迭代码选择算法的流程图

3 仿真实验

本文与文献[5-9]所得信号集的性能指标对比如表1所示。表1中所列本文数据为100次Monte-Carlo实验的最好值,而文献[5-9]数据是引用对应文献中的最好值。信号集的大小是M=3,N=40。

表1 平均ASP和平均CP的对比

由表1可知,本文信号集的平均CP比文献[5-9]的低1～2 dB左右,而本文信号集的平均ASP比文献[5-9]的要低3～4 dB。这说明了混合输入输出算法设计所得正交相位编码信号集的自相关旁瓣峰值和互相关峰值都较低,正交性较好。主要原因分析如下。

(1)本文分别利用混合输入输出算法的2个步骤极小化基于信号集相关旁瓣总能量的代价函数E1和基于信号集相关旁瓣峰值的代价函数E2,第1步中相关旁瓣总能量的降低使得相关旁瓣峰值稳定地降低,而第2步的优化更直接地减小了相关旁瓣的峰值。文献[5-9]则是单一的针对相关旁瓣的总能量进行优化,比较而言,本文建立的代价函数较文献[5-9]更全面和有效。

(2)本文将基于相关旁瓣总能量的代价函数转化为较容易求解的形式,对输入输出算法进行了维数扩展,并且针对极小化问题中的约束条件改进了输入输出算法的物面和频谱面的约束条件,使改进的输入输出算法相比于文献[5-9]中所用的传统优化算法更适合求解本文问题,而迭代码选择算法的应用进一步降低了信号集平均ASP和平均CP的值。

图5为M=3,N=40时本文算法所得信号集的非周期自相关函数和互相关函数。由图5可得,本文信号集的非周期自相关函数的旁瓣较低,而且分布比较平坦,这说明了信号集中的每个信号均具有较好的脉冲压缩性能。由图5还可以看出,非周期互相关函数的旁瓣也较低,这表明了信号之间的干扰较小,有利于目标回波信号的分离。

当阵元数M=1时,信号集转化为单个序列。p4序列和m序列为雷达发射信号中的性能良好的单个序列,而随机相位序列由于相位没有经过优化设计,导致其性能略差。本文算法所得单个序列的ASP和ISL与p4序列、m序列和随机相位序列之间的对比在图6和图7中给出。从图6和图7可以看出,本文序列的ASP和ISL比p4序列、m序列和随机相位序列都要低,这也说明了本文算法的有效性。

图5 本文信号集的自相关函数和互相关函数

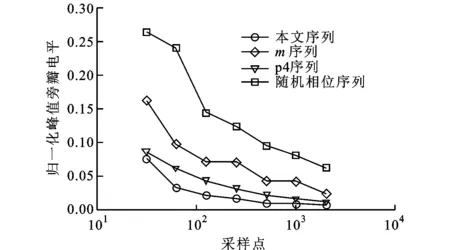
图6 序列峰值旁瓣电平的比较

图7 序列积分旁瓣电平的比较

在算法的复杂度和执行效率方面,改进的输入输出算法中的主要运算是快速傅里叶变换和快速逆傅里叶变换,所以运算时间大致以O(MNlbN)增加,而迭代码选择算法的时间复杂度近似为O(M2N2(M-1))。表2给出了设计M=3,N=40大小的信号集时本文算法和文献[5-9]算法的运行时间对比(仿真PC机配置:主频为2.50GHz和2.29 GHz的双核处理器,内存为1.98 GB,程序采用Matlab语言编写,由于与文献编程方式可能不尽相同,为了使程序运行时间具有可比性,仅列出时间的数量级)。从表2可以看出,在设计相同规模的信号集时,本文算法需要的时间比文献[7]的要长些,与文献[6,9]所需时间是同一数量级,而文献[5]和文献[6]算法所需时间较长。

表2 本文算法与文献[5-9]算法的运行时间对比

图8 平均ASP和平均CP随M的变化关系

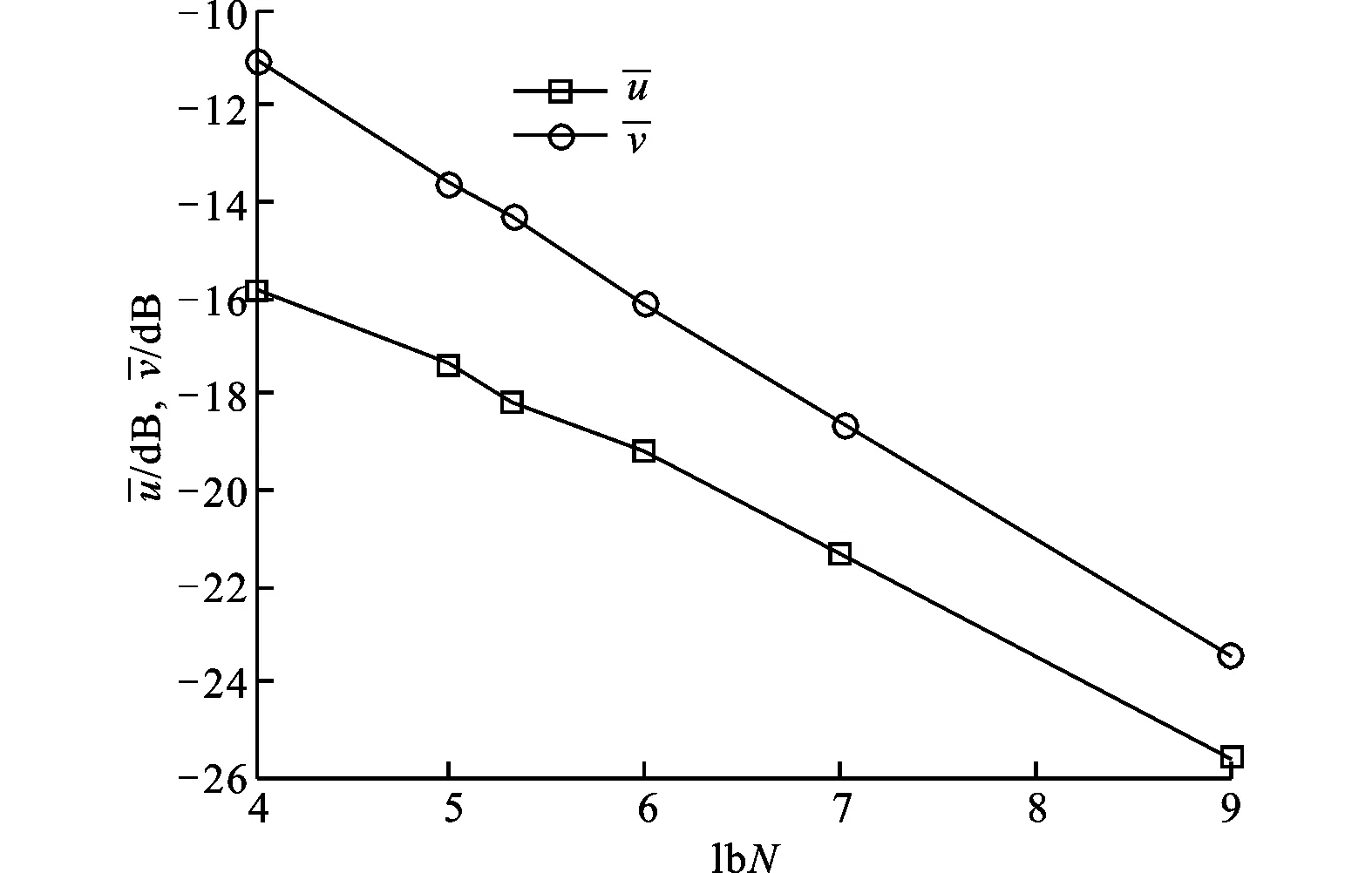
图9 平均ASP和平均CP随N的变化关系

当N=64时,本文信号集的平均ASP和平均CP随M的变化关系如图8所示,而当M=4时,本文信号集的平均ASP和平均CP随N的变化关系如图9所示。由图8和图9可得,信号集的码长不变时,平均ASP与平均CP随发射阵元数的增多而逐渐增大,而当发射阵元数不变时,平均ASP与平均CP和lbN呈现出负线性的关系。

4 结 论

针对MIMO雷达正交相位编码信号设计中,已有方法所得信号集的相关旁瓣较高的问题,本文提出了一种混合输入输出算法。该算法是由改进的输入输出算法和迭代码选择算法组成的混合优化算法。利用混合输入输出算法的2个步骤分别极小化基于信号集相关旁瓣总能量的代价函数和基于信号集相关旁瓣峰值的代价函数,最后得到相关性能较好的正交信号集。仿真结果验证了本文算法的有效性。

[1] LI J, STOICA P. MIMO radar with colocated antennas [J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114.

[2] ZHENG Guimei, CHEN Baixiao, YANG Minglei. Unitary ESPRIT algorithm for bistatic MIMO radar [J]. Electronics Letters, 2012, 48(3): 179-181.

[3] CHONG C Y, PASCAL F, OVARLEZ J P, et al. MIMO radar detection in non-Gaussian and heterogeneous clutter [J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 115-126.

[4] SONG Xiufeng, WILLETT P, ZHOU Shengli, et al. The MIMO radar and jammer games [J]. IEEE Transactions on Signal Processing, 2012, 60(2): 687-699.

[5] DENG H. Polyphase code design for orthogonal netted radar systems [J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3126-3135.

[6] LIU Bo, HE Zishu, ZENG Jiankui, et al. Polyphase orthogonal code design for MIMO radar systems [C]∥Proceedings of International Conference on Radar. Piscataway, NJ, USA: IEEE, 2006: 1-4.

[7] HE H, STOICA P, LI J. Unimodular sequence sets with good correlations for MIMO radar [C]∥Proceedings of 2009 IEEE Radar Conference. Piscataway, NJ, USA: IEEE, 2009: 1-6.

[8] KHAN H A, ZHANG Y, JI C, et al. Optimizing polyphase sequences for orthogonal netted radar [J]. IEEE Signal Processing Letters, 2006, 13(10): 589-592.

[9] GARTZ K J. Generation of uniform amplitude complex code sets with low correlation sidelobes [J]. IEEE Transactions on Signal Processing, 1992, 40(2): 343-351.

[10]FIENUP J R. Phase retrieval algorithms: a personal tour [J]. Applied Optics, 2013, 52(1): 45-56.

[11]BURVALL A, LUNDSTROM U, TAKMAN P A C, et al. Phase retrieval in X-ray phase-contrast imaging suitable for tomography [J]. Optics Express, 2011, 19(11): 10359-10376.

[12]RICARDO A O, YOBANI M B. Gerchberg-Saxton algorithm applied to a translational-variant optical setup [J]. Optics Express, 2013, 21(16): 19128-19134.

[13]CHEN Wen, CHEN Xudong. Optical multiple-image authentication based on modified Gerchberg-Saxton algorithm with random sampling [J]. Optics Communications, 2014, 318: 128-132.

[14]MEMMOLO P, MICCIO L, MEROLA F, et al. Investigation on specific solutions of Gerchberg-Saxton algorithm [J]. Optics and Lasers in Engineering, 2014, 52: 206-211.

[15]INDIRESAN P V, UTTARADHI G K. Iterative method for obtaining good aperiodic binary sequences [J]. Journal of Optimization Theory and Applications, 1971, 7(2): 90-108.

[16]杨晓超, 刘宏伟, 王勇, 等. 利用多输入多输出雷达低秩杂波的降维空时自适应算法 [J]. 西安交通大学学报, 2012, 46(8): 76-81. YANG Xiaochao, LIU Hongwei, WANG Yong, et al. A new reduced dimensional space-time adaptive processing algorithm exploiting low-rank clutter for multiple-input multiple-output radar [J]. Journal of Xi’an Jiaotong University, 2012, 46(8): 76-81.

[17]SOLTANALIAN M, NAGHSH M M, STOICA P. A fast algorithm for designing complementary sets of sequences [J]. Signal Processing, 2013, 93: 2096-2102.

[18]王旭, 纠博, 周生华, 等. 基于脉冲串编码的MIMO雷达距离旁瓣抑制方法 [J]. 电子与信息学报, 2012, 34 (12): 2948-2953. WANG Xu, JIU Bo, ZHOU Shenghua, et al. Range sidelobes suppression for MIMO radar with pulse train coding [J]. Journal of Electronics and Information Technology, 2012, 34(12): 2948-2953.

(编辑 刘杨)

ADesignMethodforMulti-InputMulti-OutputRadarPhaseCodingSignal

DU Xiaolin,SU Tao,ZHU Wentao,ZHANG Long

(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

In the design of orthogonal phase coding signals for multi-input multi-output (MIMO) radar, a new method is presented to solve the problem that the signal sets obtained by the existing algorithms have high integrated sidelobes after matched filtering. An optimization cost function based on the total correlation sidelobes energy of the signal set is converted into a simpler quadratic optimization problem. An input-output algorithm is amended and extended to multidimensional case to improve the constraints of object domain and frequency domain, and the improved input-output algorithm is used to get a solution of the simplified optimization problem. Then, the results from the first step are further optimized by minimizing the correlation sidelobes by using the iterative code selection method, and the signal set with low correlation sidelobes is finally generated. Simulation results and comparisons with the simulated annealing algorithm and the sequential quadratic programming(SQP) algorithm, etc. show that the average autocorrelation sidelobe peak and the average crosscorrelation peak of the signal set obtained by the presented method decrease by about 3-4 dB and 1-2 dB, respectively.

radar; multiple input multiple output; iterative code selection method; phase coding

2014-05-07。

杜晓林(1985—),男,博士生;苏涛(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61001204);中央高校基本科研业务费专项资金资助项目(JY0000902020);中国博士后科学基金资助项目(2013M542329);陕西省自然科学基础研究计划资助项目(2012JM8015)。

时间:2014-09-22

10.7652/xjtuxb201412015

TN957

:A

:0253-987X(2014)12-0093-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20140922.1520.003.html