采用子孔径分割的逆合成孔径雷达成像包络对齐方法

董祺,张磊,徐刚,邢孟道

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

采用子孔径分割的逆合成孔径雷达成像包络对齐方法

董祺,张磊,徐刚,邢孟道

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

针对低信噪比情况下难以对逆合成孔径雷达(ISAR)目标回波进行精确包络对齐的问题,提出了一种采用子孔径分割的逆合成孔径雷达成像包络对齐方法。该方法首先将全孔径划分为若干个相同长度的子孔径,并将每个子孔径的包络误差建模为线性,然后利用最小熵准则对子孔径包络误差进行估计,最后通过高阶多项式拟合实现对全孔径包络误差的精确估计。该方法具有更好的抗噪性和更高的估计精度,能对ISAR目标回波数据进行较为精确的包络误差补偿。仿真结果表明,在-5 dB的低输入信噪比下,相对于传统方法,该方法成像结果的熵值降低了约0.6,说明取得了更好的包络对齐结果。

逆合成孔径雷达;低信噪比;包络对齐;子孔径;高阶多项式

逆合成孔径雷达(inverse synthetic aperture radar, ISAR)的关键技术包括平动补偿和转台成像等,其中平动补偿又分为包络误差补偿和相位误差补偿2个步骤。包络误差补偿一般利用包络对齐技术实现。精确的包络对齐是相位误差补偿的基础,又是对目标进行高分辨成像的前提条件。因此,包络对齐技术已成为ISAR成像领域研究的热点之一[1-2]。

1980年代初期由Chen等提出包络对齐的互相关法[3]以来,国内外学者又相继提出了多种ISAR的包络对齐算法,大致可分为2类:第1类是最大相关处理方法[3-4],此类方法运用相邻距离像的相关性估计目标回波的包络徙动量,然后进行包络对齐处理,但其具有较强的噪声敏感性;第2类是整体最优准则处理方法[5-6],通常以平均距离像的熵最小或对比度最大为准则,通过优化算法求解各次回波间的包络偏移来进行包络对齐处理,此类方法利用了整体回波距离像的相关性信息,对噪声和散射起伏都具有较好的抑制作用,但一般需对全孔径包络误差进行搜索,相对于第1类方法运算量增大。实质上,2类包络对齐算法都是基于回波数据的相关性进行处理,在低信噪比条件下存在一定的缺陷。由于ISAR目标成像需要利用上百次回波(总转角一般要求3°～5°),所以强噪声的存在会产生较大的包络误差积累,造成包络漂移,实录数据还会产生回波突跳的现象,即突然有个别回波的距离像相对之前的回波有明显变化,然后又恢复正常,造成包络突跳[6]。强噪声的影响和回波信号突跳都会影响传统算法的包络对齐精度,从而影响最终的ISAR成像。

因为传统包络对齐方法只着眼于回波数据的相关性,而没有利用观测目标的运动特性,所以易受到强噪声和回波信号突跳的影响,具有较强的噪声敏感性。在实际ISAR成像中,一定的观测时间内,目标的平动一般较为平稳,回波信号的包络误差调制也是平稳连续变化的,而且包络对齐的精度仅要求在距离分辨单元数量级(一般在米级或者分米级),所以在包络对齐处理中,根据上述平稳运动特性,将包络误差建模为慢时间的高阶多项式形式,就能够有效克服低信噪比情况下包络误差估计的突跳问题。

针对传统包络对齐方法的噪声敏感性,本文提出一种采用子孔径分割的ISAR包络对齐方法。区别于最大相关处理方法和整体最优准则的对齐方法,本文方法利用了观测目标连续平稳的运动特性,对子孔径和全孔径包络误差分别进行线性和高阶多项式建模,在一定程度上抑制了包络突跳产生的影响;本文方法的包络误差求解运用了最小熵准则,能够实现对子孔径包络误差较为精确的估计,有效提升包络对齐精度。

1 ISAR回波包络误差建模

对ISAR成像的研究通常是基于目标的转台模型,即对非合作目标进行平动补偿后,将目标的运动等效为相对雷达的匀速转动。图1给出了目标的运动分解模型。

图1中,目标由位置1到位置2的运动,可等效为先从位置1沿径向移动到位置3(平动部分),然后旋转Δθ角度(转动部分),再从位置3沿圆周移动到位置2(绕动部分)。其中,绕动部分不提供多普勒信息,在ISAR成像中可以忽略。所以目标相对雷达运动就可以分解为平动和转动2个部分。目标平动对应的各个散射点的多普勒完全相同,对雷达成像没有贡献,但会引起多普勒展宽,需要加以补偿[5,7],以便进行后续的成像处理,而平动补偿的第1步就是包络对齐,这正是本文研究的内容。

图1 ISAR中目标运动分解模型

假设雷达观测时间为T,在方位慢时间tm(-T/2≤tm≤T/2)时刻,目标上某一点p到雷达的瞬时距离表达式为

Dp(tm)=R0+ΔR(tm)+xpsinωtm+ypcosωtm

(1)

式中:R0为目标与雷达间的初始距离;ΔR(tm)为目标平动引起的距离变化;(xp,yp)为p点在成像平面的直角坐标;ω为目标转动角速度。

在接收ISAR回波信号后,对其回波进行距离脉冲压缩处理,处理后的回波信号形式为[8]

(2)

式中:tk为快时间;B为发射信号频谱宽度;σp为目标上散射点的复散射系数;c为光速;fc为雷达发射信号载频。回波信号中包含的ΔR(tm)即为包络对齐处理中需要补偿的部分,补偿的精度会影响后续的ISAR成像。不精确的包络对齐将导致同一个目标的能量散布到相邻的几个距离单元,从而影响后续自聚焦处理的精度,造成图像在方位向散焦。

由于目标通常在观测时间内的运动轨迹连续并且较为平稳,且一般成像处理中只要求包络对齐精度达到1/2个距离分辨单元[10],所以采用高阶多项式近似包络误差函数就能够满足包络对齐所需精度。因此,本文将包络误差进行高阶多项式建模,构造包络误差函数为

(3)

式中:Q为包络误差拟合的阶数;q为慢时间tm的阶数,q=1,2,…,Q。Q值选取得越大,包络误差拟合的精度就越高,但会造成运算量增加,实际处理中需要依据包络对齐精度和运算时间要求合理选择Q值。

2 子孔径分割的ISAR包络误差求解

在进行ISAR二维高分辨成像特别是针对空间弱小目标的成像中,目标距离远、散射截面积小、存在空间杂波以及为了提升雷达抗截获能力需要发射低峰值功率的信号等原因,都将导致回波信噪比低[9]。在这种强噪声条件下,运用最大相关准则的方法已经很难实现回波信号的包络对齐。虽然基于整体最优准则的方法(以最小熵算法为例)通常有比相关类方法更优越的噪声抑制能力,更适于低信噪比情况的ISAR成像,但其仍存在包络误差估计突跳的问题,因此有必要研究在低信噪比情况下如何有效进行精度较高且快速的包络对齐处理。

针对以上问题,本文提出了一种采用子孔径分割的ISAR包络对齐方法。该方法将全孔径观测均匀划分为若干个相同长度的子孔径,利用最小熵算法估计精度较高的优势,对各个子孔径进行包络误差估计,然后利用估计的子孔径包络误差进行全孔径包络误差的高阶多项式拟合。

2.1 包络误差求解

包络误差求解步骤如下。

(1)首先将全孔径时间分为M个子孔径,每个子孔径长度相同。当M足够大时,即每个子孔径的方位向采样时间足够小,近似认为动目标在这段时间内的速度不变,所以可将包络误差近似为线性,简化了子孔径的包络误差模型。分别对每个子孔径作线性拟合。采用最小熵准则对每个子孔径的线性系数进行搜索,得到线性系数估计向量,即为一阶包络误差导数向量

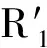
(4)

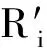
(2)对式(3)求导可以得到一阶包络误差导数为

(5)

(3)用每个子孔径的中心时刻构造时间序列α=[t1,t2,…,ti…,tM-1,tM]T,则

(6)

式中:β=[a1,a2,…,aQ]T为包络误差系数矩阵。

(4)对于ξ=Φβ形式的超定矩阵,此处采用最小二乘法实现对包络误差多项式系数β的估计

(7)

利用式(7)估计多项式系数需要(ΦTΦ)可逆,则至少需要M≥Q。

经过一次高阶拟合处理后,包络形式更为平滑,可以减小子孔径的数量M,并且可根据补偿后的包络误差曲线的形状再次选取全孔径拟合阶数Q。由式(6)和(7)可知,子孔径数越多,能估计的包络误差阶数也越高,当减少子孔径数时,能估计的阶数也会降低。所以,要在满足M≥Q的条件下合理选取Q和M。重复执行上述5个步骤,直到包络误差估计精度达到实际ISAR成像工作的需求。本文方法的实施流程如图2所示。

图2 本文方法的实施流程

2.2 参数选择

2.2.1 参数M的选择 初始子孔径数选为M,选取原则是使得每个子孔径的包络误差小于1/2距离单元[10]。采用文献[11]中所述的自适应参数选取的思想对参数M进行选取,具体操作如下。

(1)用最小熵准则对每个子孔径包络误差进行线性拟合,得到第p个子孔径包络误差为ΔRp(tm),(2p-2)T/(2M)-T/2≤tm≤2pT/(2M)-T/2。

(2)将子孔径数增加1倍,则原来的第p个子孔径被分成2个相等的子孔径,对应的包络误差为

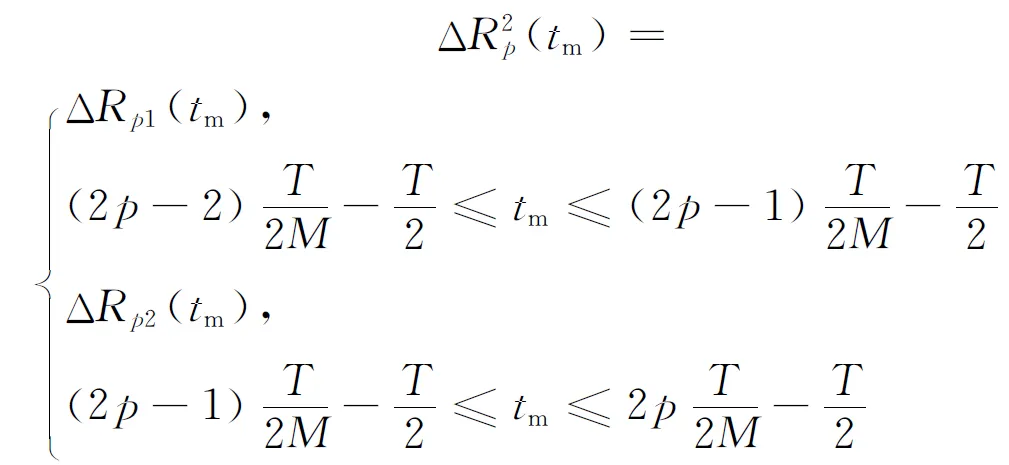
(8)

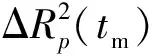
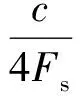
(9)

式中Fs为距离向采样频率,那么可以认为2次包络对齐结果一致。此时M的大小可以满足要求,不需要进一步增加初始子孔径数。

(4)若M不满足要求,则将初始子孔径数增加1倍,重复步骤(1)～(3),直到满足式(8)、式(9)。

参数M的选择过程如图3所示。在参数M的选择过程中,其运算主要包括熵值计算和逆傅里叶变换,其中逆傅里叶变换的运算量是组成整体运算量的最主要部分,所以参数M选择过程的运算量为O(NaNrlbNr),其中Na和Nr分别是每个子孔径的方位采样点数和距离采样点数。

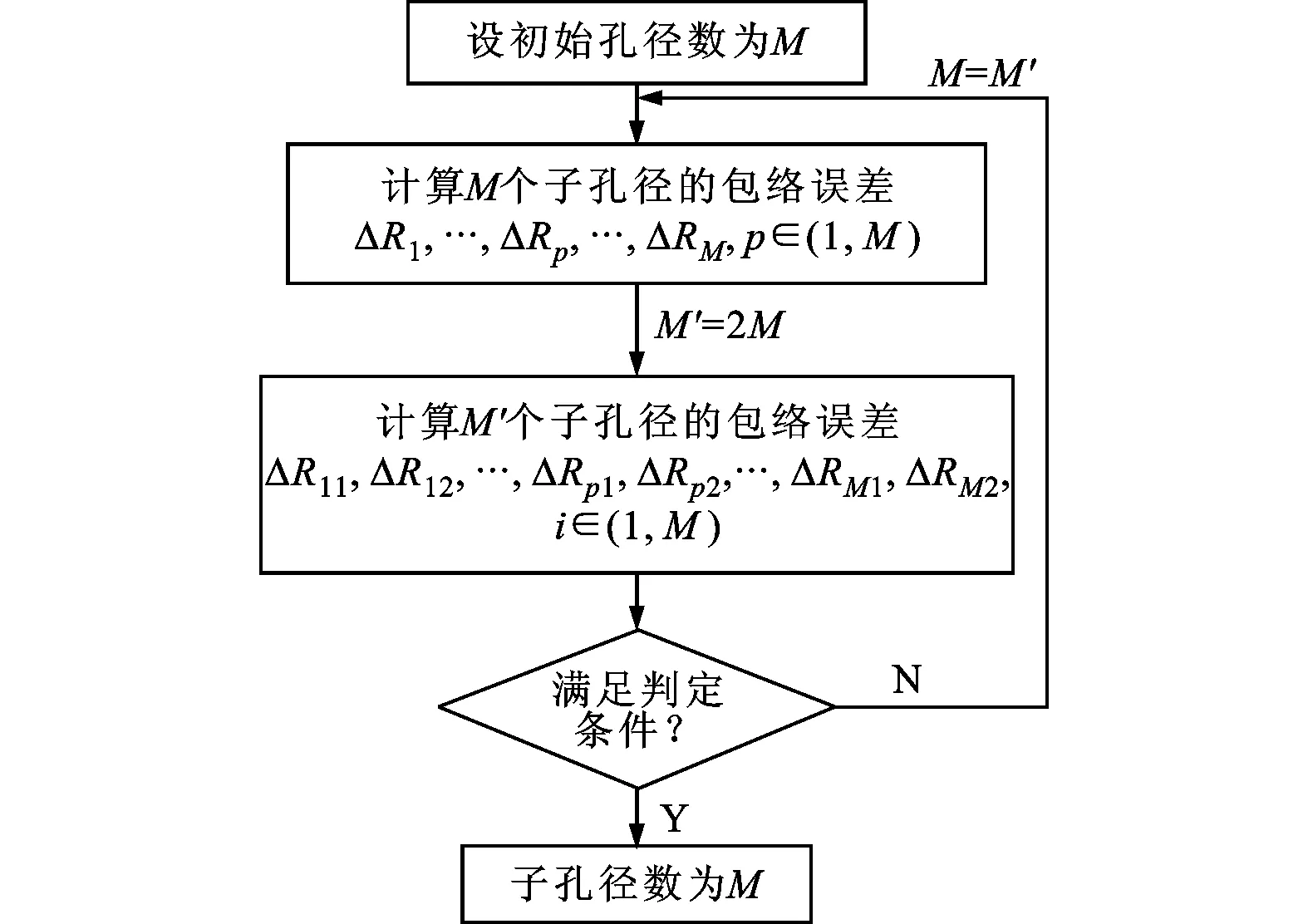
图3 参数M的选择流程图

2.2.2 参数Q的选择 合理选取了初始子孔径数M后,需要确定初始包络误差阶数Q。由于ISAR成像包络误差精度要求为1/2距离单元[10],而包络误差高阶部分的系数一般都非常小,因此对包络对齐质量的影响可以忽略。根据上述性质合理选择Q值,具体操作如下:

(1)选取初始包络误差阶数为Q,求得Q阶包络误差系数[a1,a2,…,aQ]T,代入式(3)得到第1次全孔径包络误差ΔR(1)(tm),-T/2≤tm≤T/2;

(2)将阶数增加1,求得(Q+1)阶包络误差系数[a1,a2,…,aQ+1]T,代入式(3)得到第2次全孔径包络误差ΔR(2)(tm),-T/2≤tm≤T/2;

(3)若ΔR(1)(tm)和ΔR(2)(tm)满足式(10),使得相邻2次全孔径包络补偿的差异小于1/2距离单元[10],则Q已经满足ISAR成像精度要求

|max(ΔR(1)(tm)-ΔR(2)(tm))-

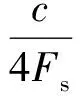
(10)

(4)若当前Q值不满足要求,则将初始包络误差阶数加1,重复步骤(1)～(3),直到满足式(10),认为更高阶的包络误差分量已经足够小,不会影响成像质量。

参数Q的选择过程如图4所示。运用2.1节所述内容求解包络误差系数时,运算量主要是由式(7)中矩阵求逆构成的,所以参数Q选择过程的运算量是O(Q3)。

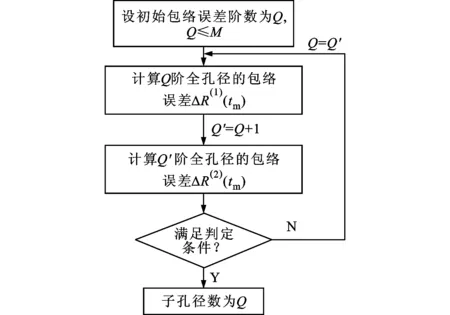
图4 参数Q选择流程图

3 实测数据处理结果与分析

下面对ISAR实测数据进行仿真实验,通过比较本文方法和基于平均距离像的相关包络对齐方法(GRA)[12]以及基于整体最优准则的最小熵方法(MEA)[13]的处理结果,验证本文方法的有效性。

ISAR数据相对较小,在本文仿真实验中,以Yak-42飞机的实测数据为例,其中心频率为5.52 GHz,发射信号带宽为400MHz,脉冲重复频率为100Hz。该数据由256次回波组成,每次回波有256个距离离散采样。在实测数据中加入目标平动对应的距离误差调制,其中包络误差曲线如图5a中实线所示。

首先利用GRA方法、MEA方法以及本文方法对实验数据进行包络对齐,为了保证包络对齐精度,在进行相关处理时对数据进行8倍插值处理。为验证本文算法在低信噪比情况下的有效性,在回波数据中加入高斯噪声以降低回波数据的信噪比。通过一系列仿真实验,发现当信噪比为-2 dB时,2种传统算法只能得到模糊的飞机成像结果,在更低的信噪比下,已经难以分辨飞机的包络。为便于进行对比,本仿真实验将信噪比设置为-2 dB,其中信噪比定义为信号功率均值与噪声方差的比值。

分别采用本文方法、GRA方法和MEA方法对包络误差进行估计,仿真结果如图5所示。由图5可见,2种传统方法的包络误差估计包含大量突跳,携带能量较大的突跳很难用一般方法去除,严重影响ISAR的方位向成像,造成方位成像的模糊,而本文方法的拟合结果与包络误差标准曲线基本一致,曲线平滑无包络突跳现象,说明本文方法对强噪声和散射起伏都有一定的抑制作用。

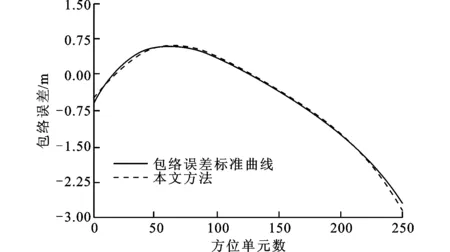
(a)包络误差标准曲线与本文方法得到的包络误差

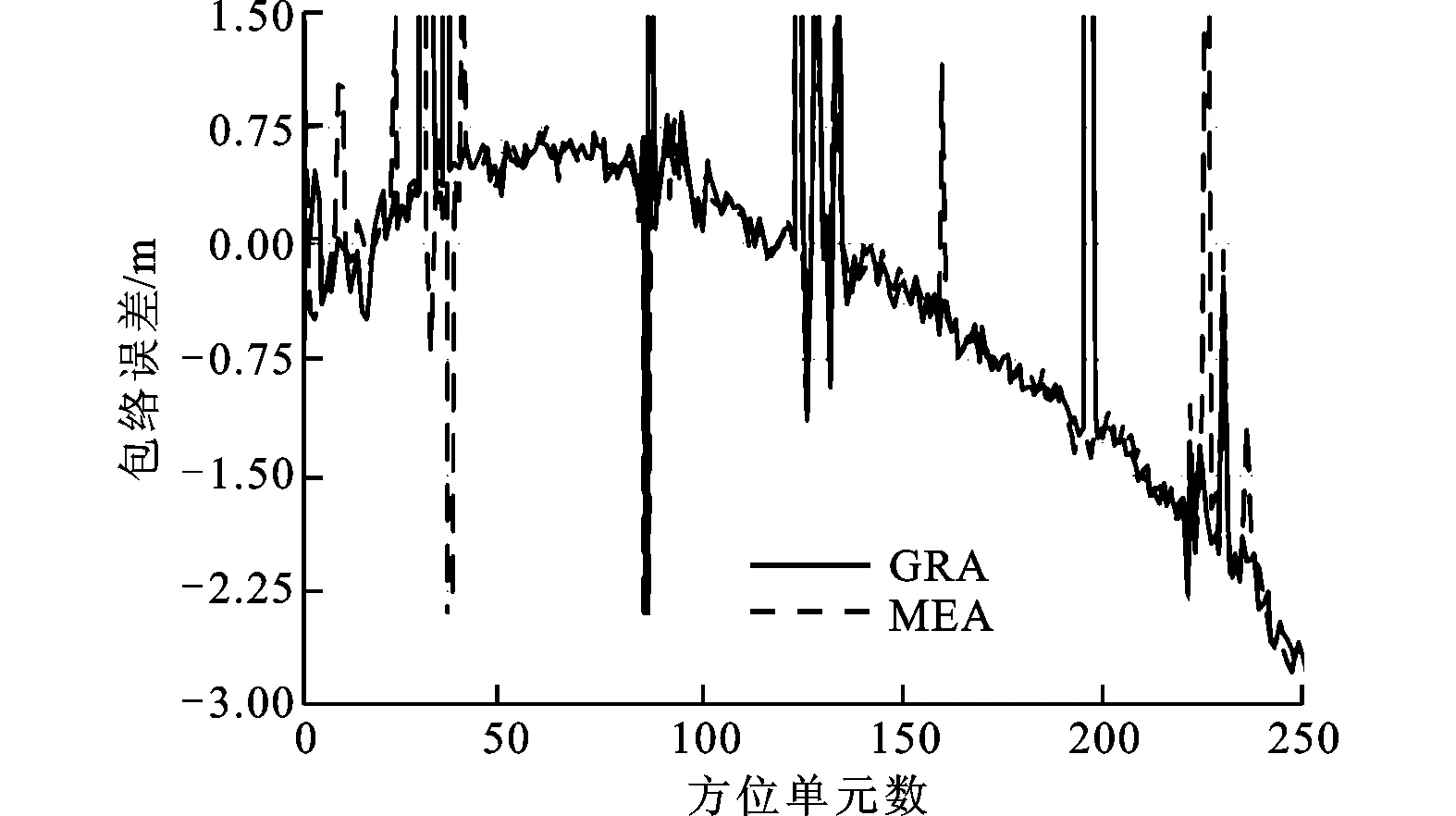
(b)GRA与MEA方法得到的包络误差

用3种方法得到的包络误差分别对回波信号进行包络补偿,得到在信噪比为-2 dB情况下的包络对齐结果,如图6所示。图6a是包络对齐处理前的包络,包络有明显的弯曲。由图6b～6d可以看出,相对于2种传统方法,本文方法的包络对齐结果更为准确,说明本文方法在低信噪比情况下要优于传统方法。

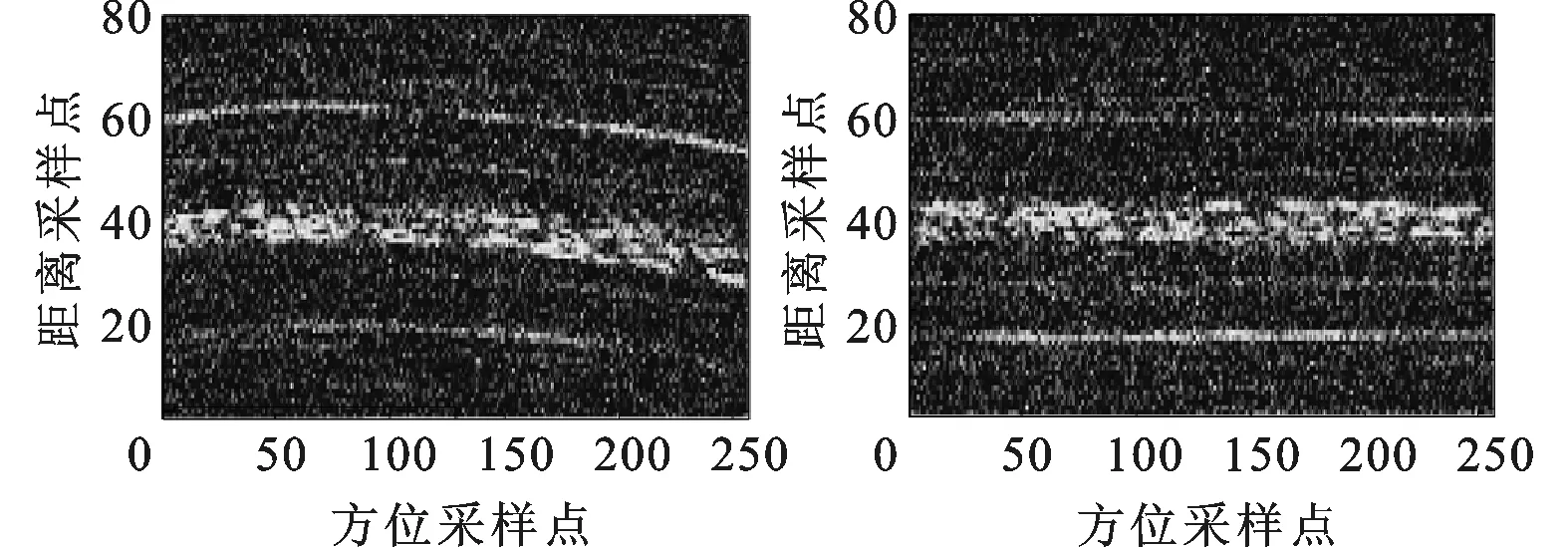
(a)包络对齐处理前 (b)GRA

(c)MEA (d)本文方法

使用多特显点法和加权最小二乘估计方法[8]对3种方法包络对齐后的数据进行自聚焦,然后进行ISAR成像,结果如图7所示。2种传统包络对齐方法的包络估计结果出现难以用一般途径消除的包络突跳现象,造成图7a～7c的成像结果出现严重的方位向散焦。相比之下,图7c成像效果远远优于图7a～7b。在更低的信噪比下,传统方法已经不能实现对回波信号的成像,图像散焦布满整个成像域,而经过对实测数据的处理,发现本文方法在-5 dB的信噪比下仍能对目标进行较为清晰的成像,体现出了新算法在低信噪比下的明显优势。

(a)GRA (b)MEA (c)本文方法

为了进一步验证本文算法的有效性,我们进行了200次Monte-Carlo实验,在不同信噪比情况下对3种方法的成像结果进行分析和比较,其信噪比设置为4、3、2、1、0、-1、-2、-3、-4、-5。使用相同的自聚焦过程处理数据,图7中成像结果的差异只是由所用3种包络对齐方法的不同决定的,所以只需利用最终成像结果的熵值和对比度作为3种包络对齐算法效果的评判标准。图8绘制了200次重复实验得到的平均熵值和对比度曲线,分别如图8a、8b所示,并给出了熵值和对比度的方差曲线,如图8c、8d所示。

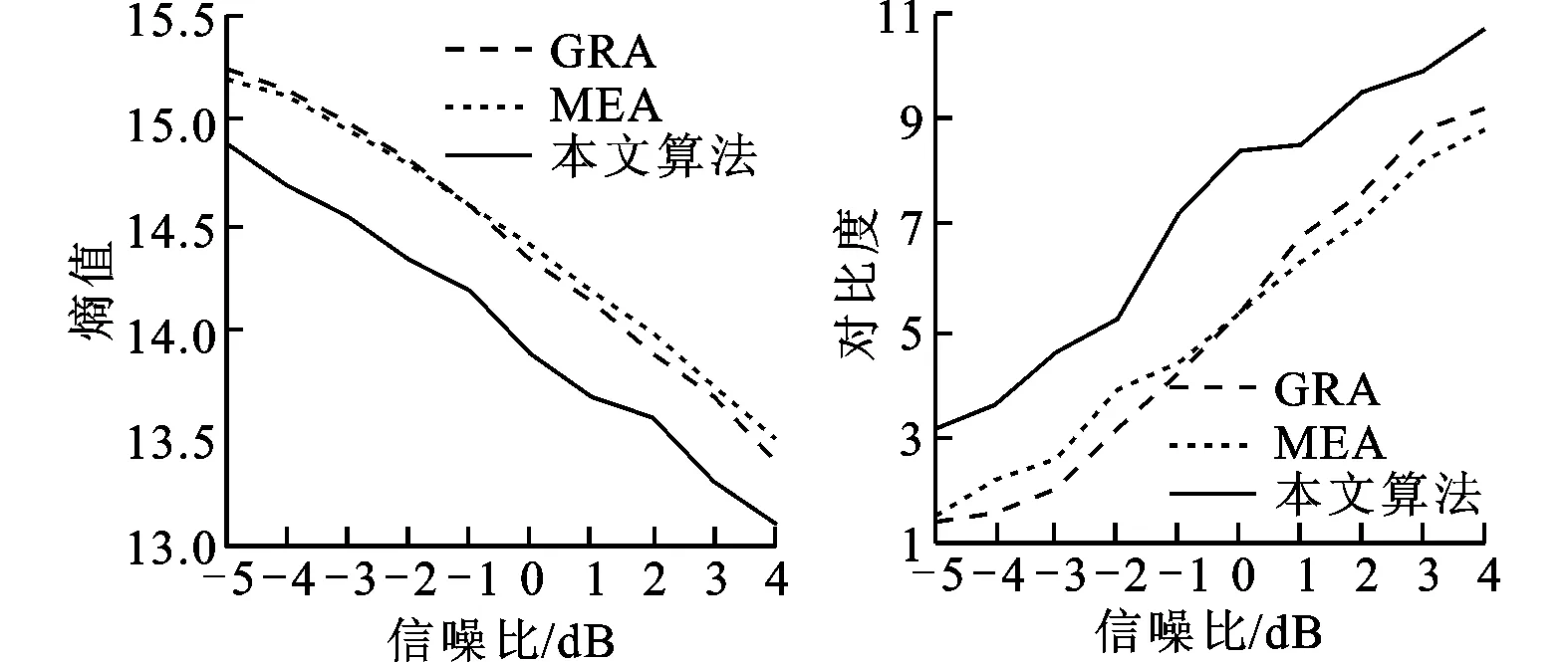
(a)信噪比-熵值曲线 (b)信噪比-对比度曲线

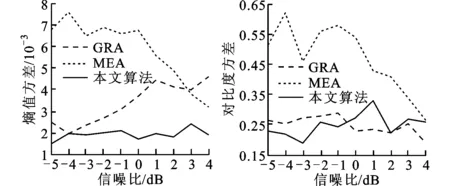
(c)信噪比-熵值方差曲线 (d)信噪比-对比度方差曲线

由图8可见,信噪比降低会造成图像的熵值增大,对比度降低。由于本文方法对包络误差的建模利用了运动的平稳连续性,一定程度上抑制了包络误差的积累和包络突跳现象,因此得到的成像结果的熵值和对比度始终优于2种传统方法。用本文方法得到的熵值和对比度的方差较小,并且在不同信噪比下平稳变化,证明了本文方法具有较强的鲁棒性。对3种方法的熵值和对比度的比较结果以及上文中的成像结果,都说明了本文方法在低信噪比情况下具有更优越的性能,进一步体现了本文方法在低信噪比情况下的包络对齐优势。

4 结 论

本文提出了一种采用子孔径分割的ISAR包络对齐方法,它将全孔径划分为若干个子孔径,对各个子孔径的包络误差进行线性建模和估计,最后利用子孔径估计结果,采用最小二乘算法实现对全孔径包络误差的高阶拟合。本文方法相对于传统包络对齐算法具有更好的抗噪性和更高的估计精度,能对ISAR目标回波数据进行较为精确的包络误差补偿,在一定程度上提高了对目标ISAR成像的质量。通过对实测数据的仿真实验和分析,验证了本文算法的有效性。

[1] XU J, LI G, PENG Y N. Parametric velocity synthetic aperture radar: signal modeling and optimal methods [J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(9): 2463-2478.

[2] WANG Junfeng, LIU Xingzhao. Improved global range alignment for ISAR [J]. IEEE Transactions on Aerospace Electronic Systems, 2007, 43(3): 1070-1075.

[3] CHEN C C, REWS H C. Target-motion-induced radar imaging [J]. IEEE Transactions on Aerospace Electronic Systems, 1980, 16(1): 2-14.

[4] DELISLE G Y, WU H Q. Moving target imaging and trajectory computation using ISAR [J]. IEEE Transactions on Aerospace Electronic Systems, 1994, 30(3): 887-899.

[5] 保铮, 邢孟道, 王彤, 等. 雷达成像技术 [M]. 北京: 电子工业出版社, 2005.

[6] ZHANG S H, LIU Y X, LI X. Pseudomatched-filter-based ISAR imaging under low SNR condition [J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(7): 1240-1244.

[7] APRILE A, MELEDANDRI D, PELLIZZERI T M, et al. Translational rotational motion compensation: a single algorithm for different radar imaging applications [J]. IET Signal Processing, 2008, 2(3): 204-215.

[8] YE W, YEO T S, BAO Y. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus [J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(5): 2487-2494.

[9] ZHANG L, LI H L, QIAO Z, et al. Integrating autofocus techniques with fast factorized back-projection for high-resolution spotlight SAR imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(6): 1394-1398.

[10]徐刚, 张磊, 陈倩倩, 等. 基于稀疏约束最优化的ISAR相位自聚焦成像算法 [J]. 电子学报, 2013(9): 1772-1777. XU Gang, ZHANG Lei, CHEN Qianqian, et al. Novel autofocusing algorithm for ISAR imaging based on sparse constraint [J]. Chinese Journal of Electronics, 2013(9): 1772-1777.

[11]WANG J F, LIU X Z. SAR minimum-entropy autofocus using an adaptive-order polynomial model [J]. IEEE Geoscience and Remote Sensing Letters, 2006, 3(4): 512-516.

[12]邢孟道, 保铮. 一种逆合成孔径雷达成像包络对齐的新方法 [J]. 西安电子科技大学学报, 2000, 27(1): 93-97.

XING Mengdao, BAO Zheng. A new method for the range alignment in ISAR imaging [J]. Journal of Xidian University, 2000, 27(1): 93-97.

[13]ZHU D Y, WANG L, YU Y S, et al. Robust ISAR range alignment via minimizing the entropy of average range profile [J]. IEEE Geoscience and Remote Sensing Letters, 2009, 6(2): 204-208.

(编辑 刘杨)

EnvelopeAlignmentAlgorithmforInverseSyntheticApertureRadarImagingBasedonSplittingSub-Apertures

DONG Qi,ZHANG Lei,XU Gang,XING Mengdao

(National Key Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

A novel envelope alignment algorithm based on splitting sub-apertures is proposed to improve the problem that it is hard for the envelope alignment to be accurately carried out under the condition of low signal to noise ratio (SNR) in inverse synthetic aperture radar (ISAR). The full-aperture is divided into several sub-apertures with same length, and a linear model is built for envelope error of each sub-aperture. The minimum entropy criterion is used to estimate the envelope error of each sub-aperture. Then a high-order polynomial is used to fit the full-aperture envelope errors, and estimations of sub-apertures are used to successfully achieve the final envelope alignment precisely. Simulation results and comparisons with the traditional envelope alignment algorithms show that the proposed method has advantages in envelope alignment, and the entropy of imaging results reduces by about 0.6 when the input SNR is as severe as -5 dB.

inverse synthetic aperture radar; low signal to noise ratio; envelope alignment; sub-aperture; high-order polynomial

2014-05-08。

董祺(1991—),女,博士生;张磊(通信作者),男,博士,副教授。

国家自然科学基金资助项目(61301280,61222108)。

时间:2014-10-31

10.7652/xjtuxb201412017

TN959.73

:A

:0253-987X(2014)12-0107-06

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1642.001.html