利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法

陈倩倩,张磊,徐刚,邢孟道,保铮

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

利用多通道联合稀疏重建的干涉逆合成孔径雷达三维成像算法

陈倩倩,张磊,徐刚,邢孟道,保铮

(西安电子科技大学雷达信号处理国家重点实验室, 710071, 西安)

针对单通道超分辨成像算法重建的超分辨图像间散射点的位置出现偏差的问题,提出了一种利用多通道联合稀疏重建的干涉逆合成孔径雷达(MCJSR-InISAR)三维成像算法。首先利用联合包络对齐算法校正目标平动对应的包络时延,再利用联合自聚焦算法实现平动补偿的初相校正,对来自不同天线的回波信号的距离差进行补偿,然后利用MCJSR进行超分辨成像,同时利用快速傅里叶变换提高运算效率,最后利用水平及俯仰干涉相位信息实现机动目标的InISAR三维成像。MCJSR-InISAR算法具有更高的强散射中心重建精度,能够对通道间的相对相位信息进行有效的保持。实测数据表明,与单通道超分辨成像算法相比,MCJSR-InISAR算法成像结果的熵值降低了约0.17,且运算复杂度降低了O(105)。

干涉逆合成孔径雷达;联合稀疏重建;三维成像;机动目标

干涉逆合成孔径雷达(interferometric inverse synthetic aperture radar, InISAR)[1-4]成像技术采用三天线相位干涉的方法获取目标的三维视图,与逆合成孔径雷达(inverse synthetic aperture radar, ISAR)获得的三维空间目标在距离多普勒平面上的二维投影图像相比,更有利于目标的识别,且信号处理过程比较简单,系统易于实现,因而受到了广泛的关注。

为了能够获取高方位分辨率,需要对回波信号进行长时间积累。然而,由于ISAR目标的机动性,对目标进行长时间驻留观测,回波信号可能存在很强的多普勒时变,并且容易受到外界环境的干扰,这会增加ISAR成像处理的复杂度,并使得图像出现散焦情况。相比而言,短相干处理时间(coherent processing interval, CPI)内,机动目标的运动接近平稳且目标的散射特性也相对稳定,因此在短CPI条件下,更易于实现机动目标的实时成像和识别[5]。但是,在短CPI内,由于回波次数较少,利用传统的ISAR成像方法如距离多普勒(range-Doppler,RD)算法,得到的图像方位分辨率较低,因此需要采用超分辨成像算法提高分辨率。传统的基于参数模型的超分辨算法,如Burg算法、RELAX算法等,对噪声和模型误差比较敏感,且观测数据长度也制约了算法的性能[6]。压缩感知(compressive sensing, CS)理论指出:在一定条件下,一个未知稀疏信号可以通过求解一个最小l-范数约束优化问题,实现从低维观测数据重建高维目标信号[7]。利用CS理论能够克服传统超分辨成像算法的缺点,获得更好成像质量的高分辨率图像。因此,自被提出至今,CS理论在超分辨雷达成像方面得到了广泛的应用[8-9]。

利用ISAR图像的稀疏性,文献[10]提出基于稀疏约束模型的InISAR三维成像算法,此算法的超分辨成像是对各个天线的回波信号进行单独处理,忽略了一个重要特性,即InISAR系统中的多通道回波信号之间具有很强的相关性,从而降低了干涉相位信息的估计精度。因此,针对短CPI内的机动目标,本文提出利用多通道联合稀疏重建(multichannel joint sparse recovery, MCJSR)的InISAR(MCJSR-InISAR)三维成像算法。该算法通过建立联合稀疏约束最优化模型进行超分辨成像,有效地利用了多通道回波信号间的相关性,提高了ISAR图像中强散射中心的重建精度,并有效地保持了通道间的相对相位信息,从而获得较高精度的干涉相位信息,实现高质量的目标InISAR三维成像。此外,对最优化问题进行求解时利用快速傅里叶变换(FFT)提高算法的运算效率,保证算法的高效性。

1 InISAR回波信号模型

为获得目标的三维图像,InISAR成像系统包含多个天线,这里以水平方向2个天线对运动目标观测时的成像几何模型为例,俯仰方向的成像几何模型与之类似。图1给出了天线与目标的几何关系。天线A与B之间的基线长度为L。在雷达照射期间,目标从位置1运动到位置2,Δθ(tm)表示散射点p(x,y)从位置1到2时相对雷达的姿态角变化。RAo′和RBo′分别表示在位置1处目标旋转中心o′到天线A与B的距离。

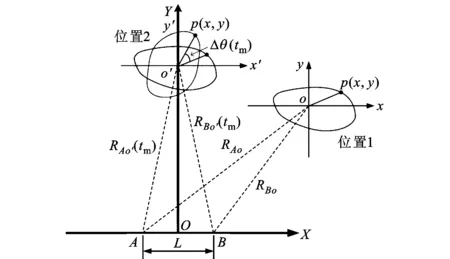
图1 天线与目标的几何关系

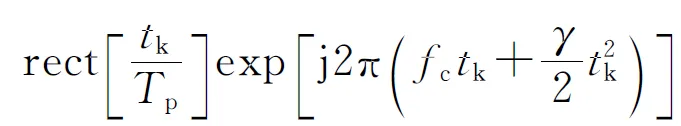
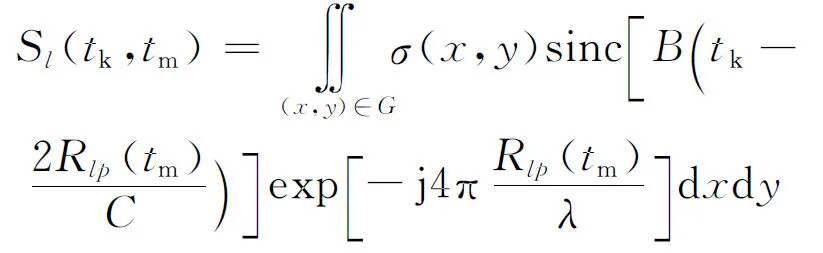
(1)

式中:l=A,B;σ(x,y)表示目标上散射点p的散射系数;G表示目标所占区域;B为信号带宽;0≤tm≤Ta为慢时间,Ta表示CPI长度;λ为波长;C为光速;Rlp(tm)表示点p到天线A和B的瞬时距离,表达式分别为

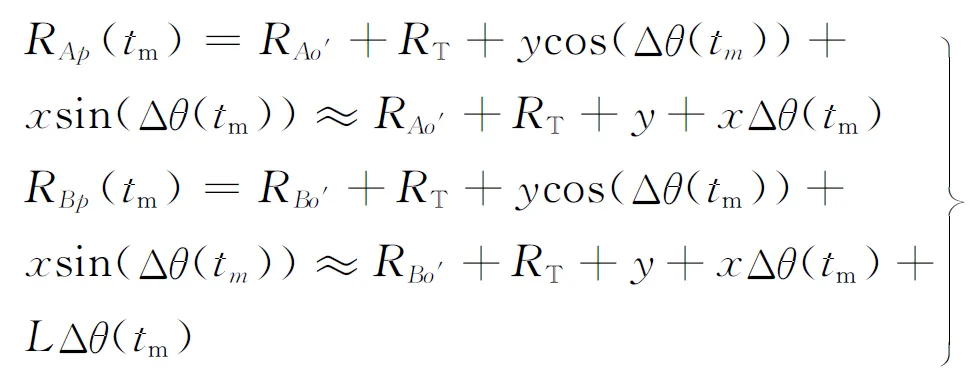
(2)

在短CPI条件下,机动目标运动近似平稳,则Δθ(tm)≈ωtm,其中ω为目标的转动速度,y+xΔθ(tm)表示散射点p相对雷达的转动引起的距离变化量,RT表示目标相对雷达的径向运动引起的变化量。为了尽可能减小通道间图像的差异,提高干涉相位的估计精度,以天线A的回波信号作为参考,采用联合包络对齐和联合自聚焦的方法对平动进行补偿[3]。LΔθ(tm)表示目标整体相对于天线A与B转动引起的波程差,这一项会使得生成的ISAR图像不能配准,可以利用文献[4]中所提出的方法,通过估计出目标的角运动参数,补偿目标整体的角运动,即补偿该波程差,得到2幅配准的ISAR图像。另外,当目标尺寸较大时可能存在越距离单元徙动现象,可利用Keystone变换对其进行校正[11]。此时,经过补偿后的信号表达式变为

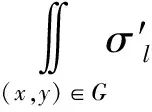
(3)

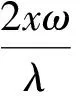
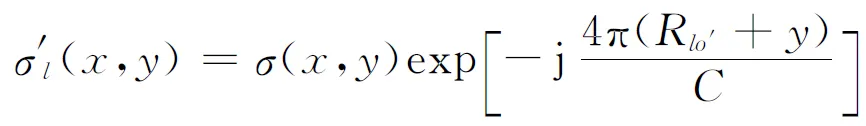
(4)

由于雷达到目标的距离远远大于目标尺寸和基线长度,将式(4)共轭相乘后得到

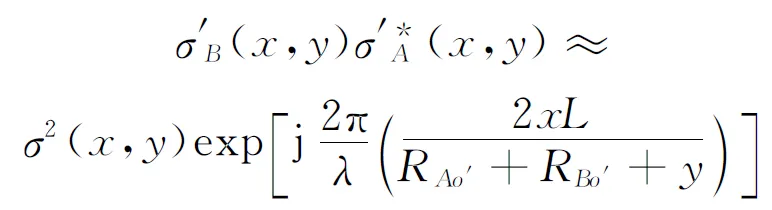
(5)

根据式(5)中的相位,可以得到散射点相对原点O的水平向真实位置信息,同理可得散射点俯仰向的真实位置信息,从而得到目标的三维视图。

2 多通道联合稀疏约束超分辨成像

对机动目标而言,在长CPI内,回波信号可能存在很强的多普勒时变,这会增加ISAR成像处理的复杂度。相比之下,由于短CPI内目标运动接近平稳且目标的散射特性也相对稳定,对目标进行短驻留时间观测更易于实时成像。因此,基于第1节所述的回波信号模型,针对短CPI内的机动目标,本文提出一种高质量的三维InISAR成像方法。

2.1 联合稀疏约束最优化模型

在短CPI内,由于回波次数较少,距离多普勒成像算法所得的图像方位分辨率较低,需要采用超分辨成像算法提高分辨率。在ISAR图像中,目标散射场的绝大部分能量仅由少数强散射点贡献,而且强散射中心仅占整个成像平面非常少的像素单元,这说明ISAR图像具有很强的稀疏性[6,8]。因此,基于ISAR图像的稀疏性,利用CS理论可以得到更好成像质量的超分辨ISAR图像[9,12]。考虑到噪声的影响,式(3)的回波信号写成矩阵形式为

sl=Φal+nl;

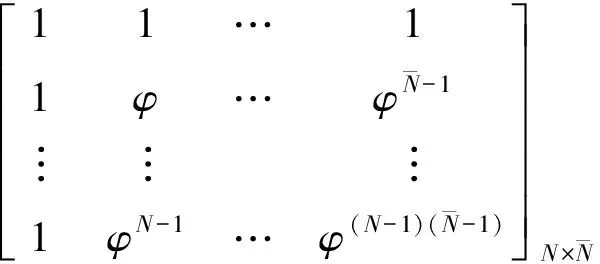
(6)

文献[10]中指出,根据贝叶斯CS,利用最大后验概率估计法,al可利用下面的稀疏约束最优化问题进行求解

(7)

式中:‖·‖q表示q-范数;μl为稀疏约束系数,用于平衡图像稀疏度和估计误差精度间的关系,需要合理选择μl的值以保证恢复数据的精确性[12]。此方法的超分辨图像是对多通道回波信号进行单独处理获取的。值得注意的是,散射点的位置信息是通过InISAR系统中相邻天线所得的2幅ISAR图像中对应散射点的相位差估计所得,换言之,为了获得高质量的目标三维视图,通道间的相对相位信息保持非常重要。此外,散射点在InISAR各通道所得的ISAR图像中的分布相同,即多通道回波信号间有较强的相关性。然而,单通道稀疏约束最优化算法忽略了这一特性,使得重建的超分辨图像间散射点的位置分布出现偏差,从而破坏了通道间的相对相位信息,降低了干涉相位信息的估计精度。因此,本文提出一种改进的超分辨成像算法,通过建立一个联合稀疏约束最优化模型求解al,其表达式为

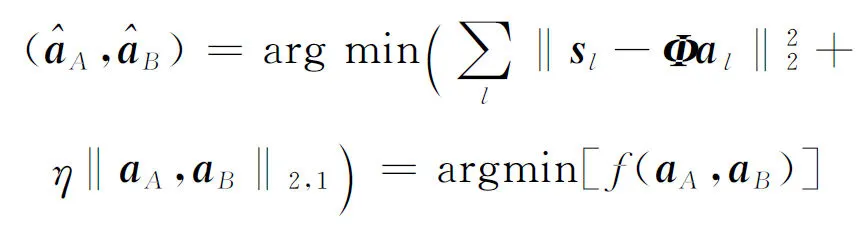
(8)

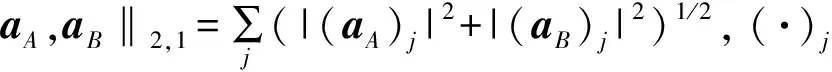
2.2 联合稀疏约束最优化求解算法

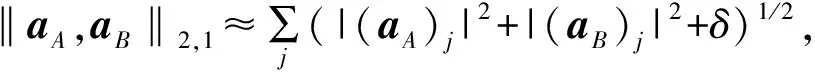
2ΦHsl=H(aA,aB)al-2ΦHsl

(9)

其中Hessian矩阵近似为

H(aA,aB)=2ΦHΦ+ηΛ(aA,aB)

(10)

且有

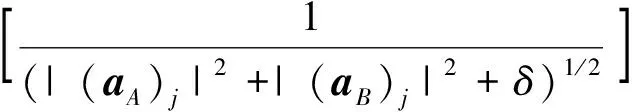
(11)

Hessian矩阵是目标函数al本身的函数,可以通过迭代方法进行求解,迭代表达式为

(12)

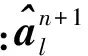
利用式(8)重建得到各个通道的超分辨ISAR图像,然后通过式(5)求出目标的三维位置信息。本文所提出的MCJSR-InISAR三维成像流程图如图2所示。

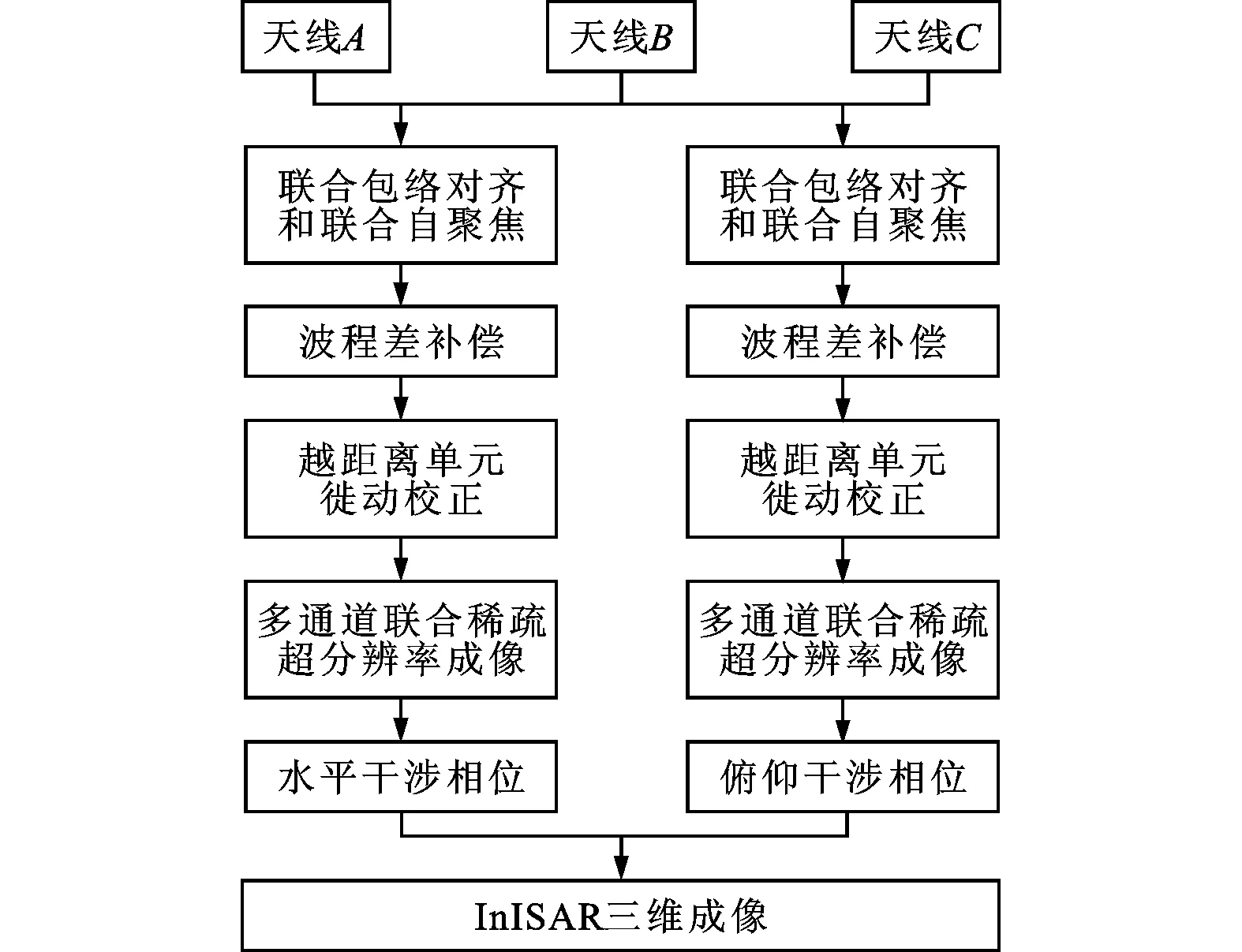
图2 MCJSR-InISAR三维成像算法流程图

3 实验结果

为验证本文所提算法的有效性,下面对雷达观测一个飞机目标的实测数据进行处理,其光学图像如图3所示,相关的雷达系统参数如下:雷达与目标的距离约为29 000m,脉冲重复频率为200Hz,波长为0.035 m。在短CPI内对目标进行观测,本文选取64个脉冲的回波数据进行处理,在实测数据处理中,方位向重建点数设为256。在超分辨处理前,将回波信号幅度归一化为200,并设置迭代门限ρ为10-4,稀疏系数η为0.015,常数δ为10-6。

图3 飞机光学图像

对目标进行长CPI观测(本实验选取256个脉冲),回波数据经联合包络对齐以及自聚焦处理后,得到的距离像如图4所示,可见越距离单元徙动现象比较明显,这增加了ISAR成像处理的复杂度。另外,选取某距离单元(如实验中选取第136个距离单元)信号,通过时频分析得到信号的时频分布,如图5所示的Wigner-Ville分布(WVD)。从图中可以看出,机动目标在长CPI观测下的多普勒谱是时变的,当利用传统的RD成像算法处理时,得到的ISAR图像会出现散焦现象。相比之下,当对目标进行短CPI观测时,平动补偿后得到的距离像如图6所示,可见越距离单元徙动现象可以忽略,并且短CPI条件下,机动目标的转动速度可以认为是恒定的,因此,短CPI观测更易于实现机动目标的成像和识别。然而,由于回波次数较少,利用传统的RD算法得到的ISAR图像方位分辨率较低,如图7所示,不利于目标的识别,因此需要采用超分辨成像算法提高分辨率。

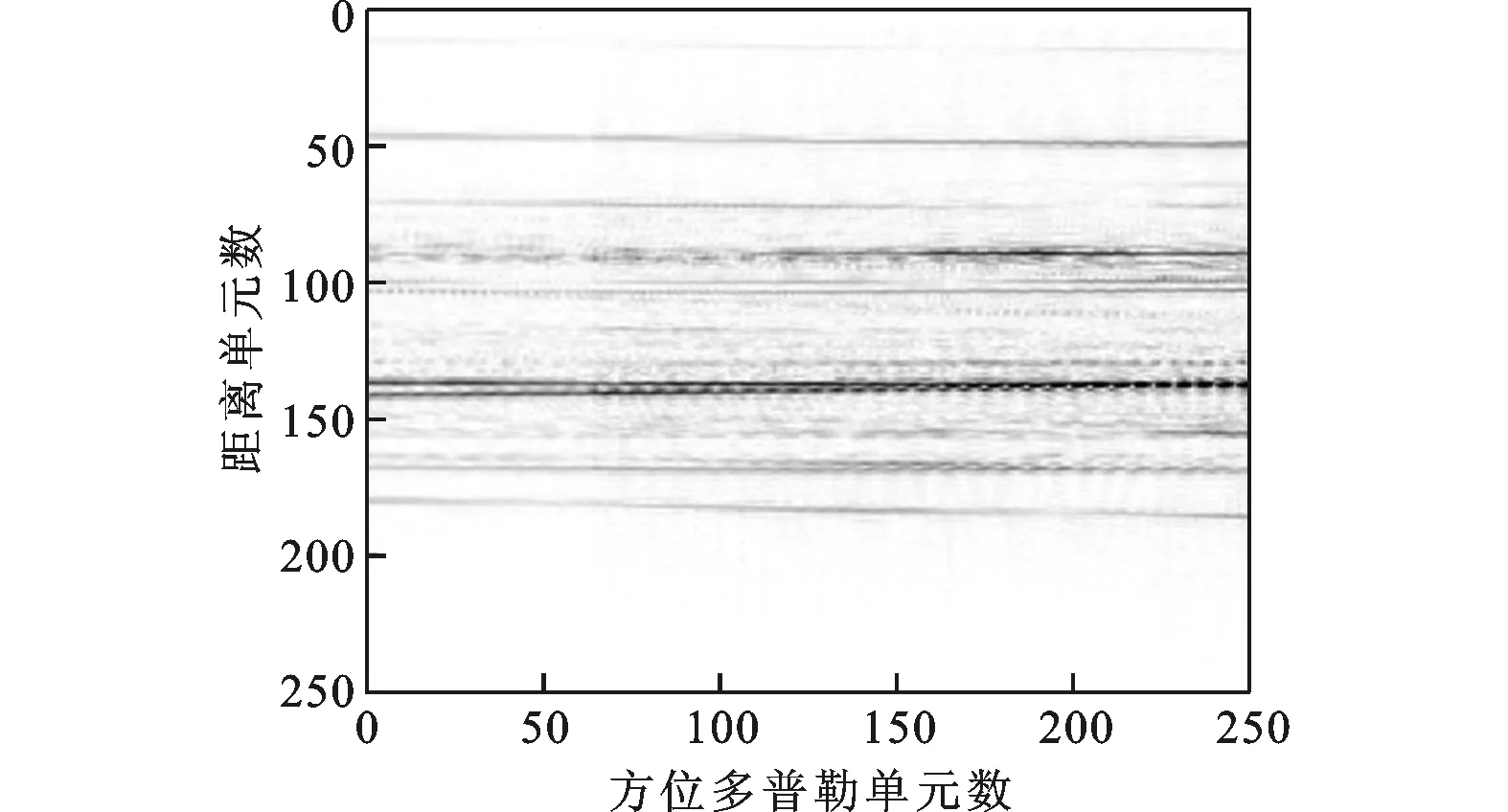
图4 长CPI下平动补偿后的距离像

图5 某距离单元信号的WVD图

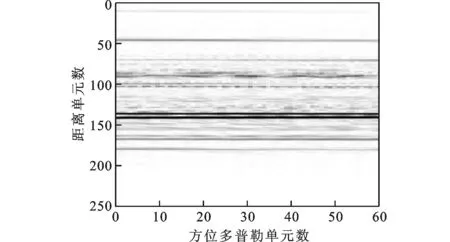
图6 短CPI条件下平动补偿后的距离像

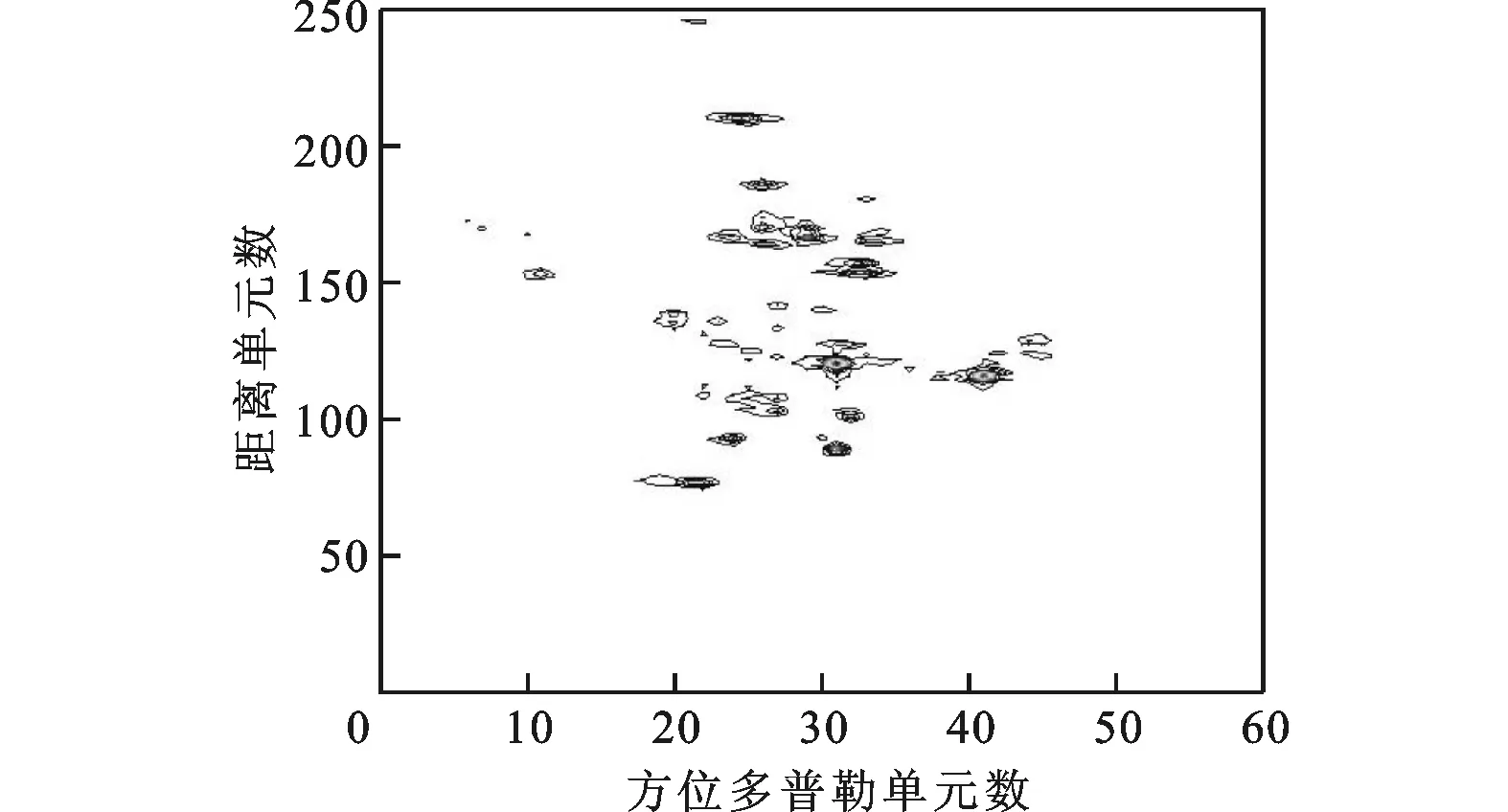
图7 短CPI条件下的RD图像

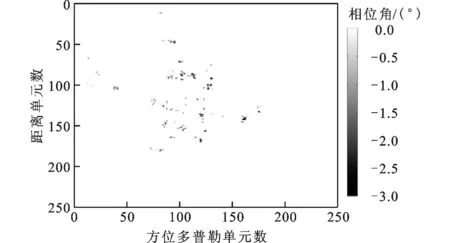
(a)利用文献[10]算法得到的水平干涉相位图

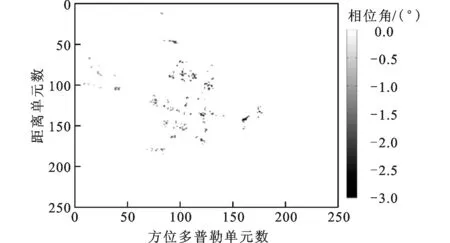
(b)利用本文算法得到的水平干涉相位图

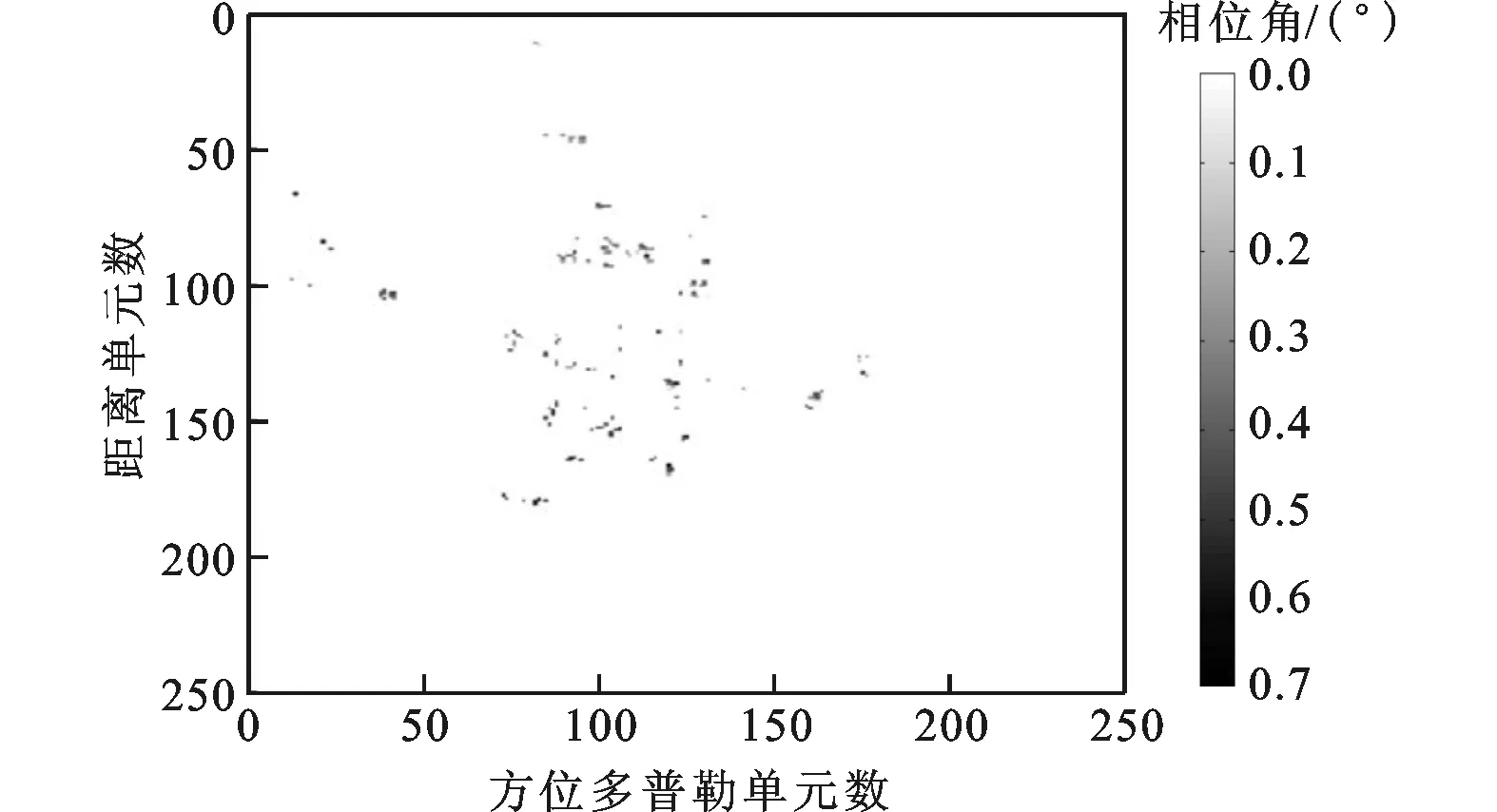
(c)利用文献[10]算法得到的俯仰干涉相位图

(d)利用本文算法得到的俯仰干涉相位图

(a)利用文献[10]算法所得的目标三维图像

按照图2所示的仿真流程,利用文献[10]中算法和本文算法对回波数据进行超分辨成像,为了分析成像算法的有效性,在此实验中提出采用图像熵作为评价成像质量的准则。以天线B为例,计算文献[10]中算法和本文算法重建得到的超分辨图像的熵值结果分别为4.406 8和4.237 6。由此可见,本文算法有效地提高了图像中强散射中心的重建精度,能够获得更好成像质量的ISAR图像。另外,对超分辨图像处理后,得到的干涉相位分布比较图如图8所示。比较图8a、c与b、d,从图中机头、机尾、机翼和机身部分也可以明显看出,与文献[10]算法相比,利用本文算法能获得精度更高的干涉相位。利用2种算法得到的目标三维图像比较图如图9所示,从图9可见,利用本文算法能够得到更清晰的目标结构特征,与图8所示的干涉相位图相符合。由此验证,本文所提出的MCJSR-InISAR三维成像算法,具有更高的散射点重建精度,且能够有效地保持通道间的相对相位信息,从而获得更好成像质量的目标三维图像,更有利于目标的识别。

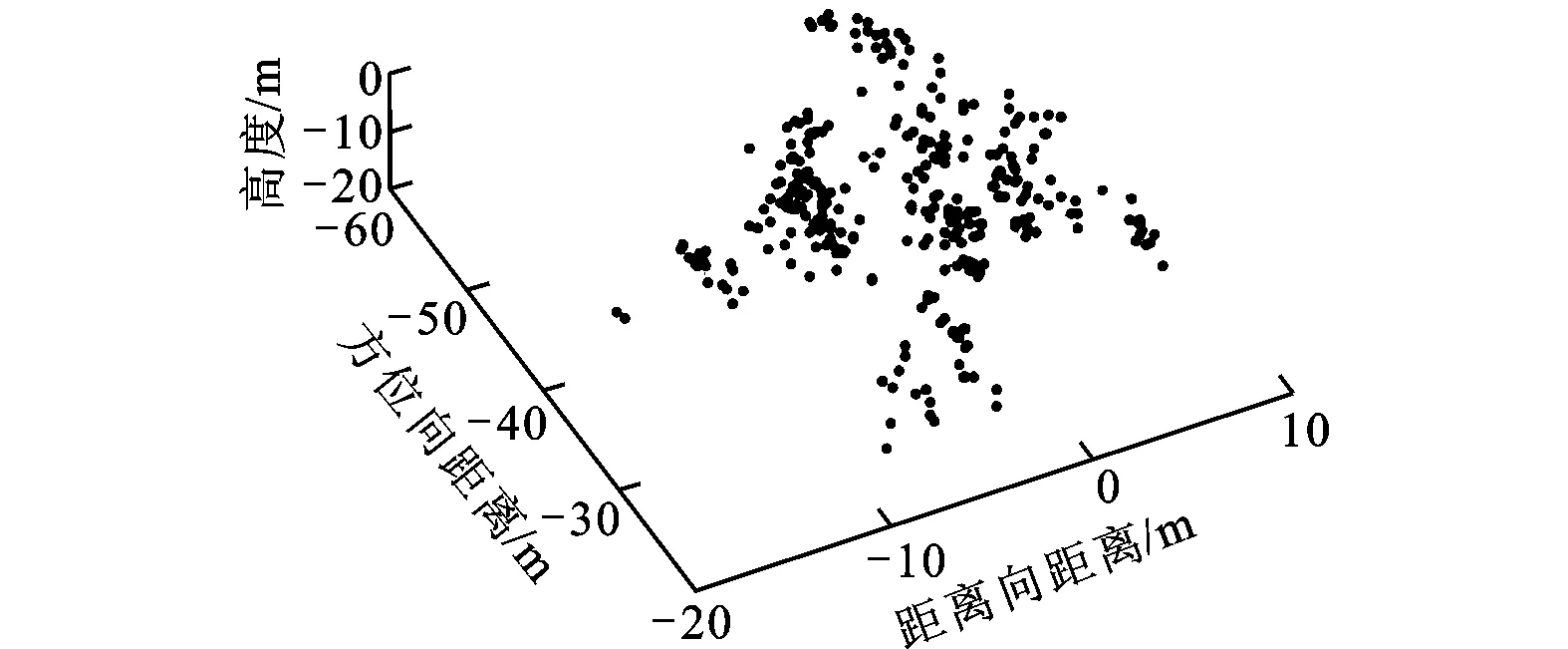
(b)利用本文算法所得的目标三维图像

最后,对实测数据处理的运算量进行分析。实验中需重建的超分辨图像大小为256×256像素,即每次迭代运算中K为65 536,Hessian矩阵的迭代运算次数NC设为200,利用本文所提算法达到设置的迭代收敛条件时,总共需要的迭代次数NQ为136,根据2.2节的分析可知,本文算法的运算复杂度为O(136×200×65536×lb65536),比直接利用Cholesky分解矩阵的求解运算量O(136×655363/3)小很多。由此证明,本文算法具有较高的运算效率。

4 结 论

本文针对短CPI内的ISAR机动目标,提出一种MCJSR-InISAR三维成像算法。基于ISAR图像的稀疏性,通过建立联合稀疏约束最优化信号模型重建超分辨ISAR图像,有效地利用了多通道回波信号间的相关性,提高了图像中散射点的重建精度,并确保了通道间相对相位信息的保持,从而提高了干涉相位的估计精度,得到更精确的目标三维位置信息。此外,利用FFT简化了最优化问题的求解,提高了算法的运算效率。经实验验证,利用本文所提算法,能够得到更高质量的目标三维视图,有利于识别目标。

[1] WANG G, XIA X, CHEN V C. Three-dimensional ISAR imaging of maneuvering target using three receivers [J]. IEEE Transactions on Image Processing, 2001, 10(3): 436-447.

[2] XU X J, NARAYANAN R M. Three-dimensional interferometric ISAR imaging for target scattering diagnosis and modeling [J]. IEEE Transactions on Image Processing, 2001, 10(7): 1094-1102.

[3] LIU Y B, SONG M C, WU K, et al. High-quality 3-D InISAR imaging of maneuvering target based on a combined processing approach [J]. IEEE Geoscience and Remote Sensing Letters, 2013, 10(5): 1036-1040.

[4] ZHANG Q, TAT S Y, DU G, et al. Estimation of three-dimensional motion parameters in interferometric ISAR imaging [J]. IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(2): 292-300.

[5] MOORE T G, ZUERNDORFER B W, BURT E C. Enhanced imagery using spectral-estimation-based techniques [J]. Lincoln Laboratory Journal, 1997, 10(2): 171-186.

[6] ZHANG L, XING M D, QIU C W, et al. Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressed sensing [J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(10): 3824-3838.

[7] CANDES E J, ROMBERG J, TAO T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509.

[8] 陈倩倩, 徐刚, 李亚超, 等. 短孔径ISAR方位定标 [J]. 电子与信息学报, 2013, 35(8): 1854-1861. CHEN Q Q, XU G, LI Y C, et al. Cross-range scaling for ISAR with short aperture data [J]. Journal of Electronics & Information Technology, 2013, 35(8): 1854-1861.

[9] 张磊. 高分辨SAR/ISAR成像及误差补偿技术研究 [D]. 西安: 西安电子科技大学, 2012.

[10]LIU Y B, LI N, WANG R, et al. Achieving high-quality three-dimensional InISAR imageries of maneuvering target via super-resolution ISAR imaging by exploiting sparseness [J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(4): 828-832.

[11]XING M D, WU R, LAN J, et al. Migration through resolution cell compensation in ISAR imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2004, 1(2): 141-144.

[12]XU G, XING M D, ZHANG L, et al. Bayesian inverse synthetic aperture radar imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1150-1154.

[13]HYDER M M, MAHATA K. A robust algorithm for joint-sparse recovery [J]. IEEE Signal Processing Letters, 2009, 16(12): 1091-1094.

[14]RICHARD G, BARANIUK V C, MARCO F D, et al. Model-based compressive sensing [J]. IEEE Transactions on Information Theory, 2010, 56(4): 1982-2001.

[15]BOYD S, VANDENBERGHE L. Convex optimization [M]. Cambridge, England: Cambridge University Press, 2004.

[本刊相关文献链接]

孟自强,李亚超,李浩林,等.双/多基地合成孔径雷达前视三维分辨力研究及运动参数设计.2014,48(8):29-35.[doi:10.7652/xjtuxb201408006]

杨桃丽,索志勇,李真芳,等.地球同步轨道合成孔径雷达干涉测量模型.2014,48(4):85-89+101.[doi:10.7652/xjtuxb 201404015]

侯兴松,张兰,肖琳.合成孔径雷达图像的贝叶斯压缩感知重构算法.2013,47(08):74-79.[doi:10.7652/xjtuxb201308013]

卢锦,苏洪涛,水鹏朗,等.辅助粒子滤波实现天波超视距雷达弱目标似然比检测.2013,47(8):93-97.[doi:10.7652/xjtuxb201308016]

朱磊,水鹏朗,章为川,等.利用区域划分的合成孔径雷达图像相干斑抑制算法.2012,46(10):83-88.[doi:10.7652/xjtuxb201210015]

李世忠,王国宏,白晶,等.压制干扰下雷达网点目标概率多假设跟踪算法.2012,46(10):101-106.[doi:10.7652/xjtuxb 201210018]

杨晓超,刘宏伟,王勇,等.利用多输入多输出雷达低秩杂波的降维空时自适应算法.2012,46(8):76-81.[doi:10.7652/xjtuxb201208014]

朱军涛,廖红建,谢勇勇,等.采用短时傅里叶变换的铁路车载探地雷达数据解译方法.2012,46(7):108-114.[doi:10.7652/xjtuxb201207020]

张立峰,王彤,吴建新,等.机载雷达目标空时参数快速估计方法.2012,46(02):135.[doi:10.7652/xjtuxb201202023]

牛威,苏威,郝培杰,等.利用雷达散射截面积序列的特定航天器工作平台分类识别方法.2011,45(12):53-58.[doi:10.7652/xjtuxb201112010]

陈士超,武其松,吴玉峰,等.一种大斜视双基地合成孔径雷达的频率变标成像算法.2011,45(10):82-87.[doi:10.7652/xjtuxb201110015]

(编辑 刘杨)

AThree-DimensionalImagingAlgorithmofInterferometricInverseSyntheticApertureRadarUsingMultichannelJointSparseRecovery

CHEN Qianqian,ZHANG Lei,XU Gang,XING Mengdao,BAO Zheng

(National Laboratory of Radar Signal Processing, Xidian University, Xi’an 710071, China)

A novel three-dimensional (3-D) imaging algorithm of interferometric inverse synthetic aperture radar (InISAR) using multichannel joint sparse recovery (MCJSR), named MCJSR-InISAR, is proposed to improve the problem that the super-resolution images recovered by the single channel super-resolution imaging algorithm do not necessarily share the same positions of the scattering centers. The combined range alignment approach is used to correct the envelope delay caused by the target’s translational motion, and then the combined phase adjustment approach is employed to complete the phase compensation of translational motion. The range differences between two echo signals

by different antennas are then compensated. Then, MCJSR is used for super-resolution imaging, and the computational efficiency of the proposed algorithm is improved by using the fast Fourier transform (FFT). Finally, a 3-D InISAR imagery of the maneuvering target is obtained by using both the horizontal and the pitching interferometric phase information. The MCJSR-InISAR algorithm can improve the recovery precision of the strong centers in the target scattering field, and preserve effectively the relative phase information between different channels. Experimental results on real-measured data and comparisons with the single channel super-resolution imaging algorithm show that the proposed algorithm decreases the entropy of the resulting image by about 0.17, and reduces the computational complexity by aboutO(105).

interferometric inverse synthetic aperture radar; joint sparse recovery; three-dimensional imaging; maneuvering target

2014-03-21。

陈倩倩(1984—),女,博士生;邢孟道(通信作者),男,教授,博士生导师。

国家自然科学基金资助项目(61301280,61001211)。

时间:2014-10-31

10.7652/xjtuxb201412016

TN957.52

:A

:0253-987X(2014)12-0100-07

网络出版地址:http:∥www.cnki.net/kcms/detail/61.1069.T.20141031.1643.018.html