基于并行处理的一种新型有效的网络架构BSN-MOT

李江昀，孙丽婷

(1. 北京科技大学 自动化学院，北京 100083；2. 北京科技大学 钢铁流程先进控制教育部重点实验室，北京 100083)

1 引言

Biswapped网络(BSN)是一种双层架构的互联网络，它提供了一种构建可扩展性、模块化、可继承性、容错性等大规模的并行计算机体系结构形式[1]。基于BSN的多处理器系统架构，是由2N个规模为N的处理器组组合而成，即含有22N个处理器。另一方面，作为非常有效的互联网络拓扑结构，MOT(mesh of tree)拥有2个非常理想的性能，即小直径及高的对分宽度，并且在只考虑速度的情况下，MOT被认为是最快速的互联网络，在解决如分组路由、排序、前置计算、矩阵乘法运算、最短路径、最近邻居等重要算法问题时，运行在MOT上的时间复杂度只达到

本文结合BSN及MOT的双重拓扑优势，提出一种新型网络架构BSN-MOT，并对新架构的模型及基本拓扑性质进行了具体分析；同时，本文研究了运行在该架构上的基本通信及应用等并行算法，并与其他2种流行的树形双层架构在算法时间复杂度上进行了比较，结果显示BSN-MOT更为快速。

其实，许多其他的树形双层架构都被研究给出，如MCT(mesh-connected tree)[2]、MMT(multmesh of tree)[3]、OMULT(optical multi-trees)[4]等。在文献[2]中，Kemal证明了MCT是比超立方体更简单，且成本更低的架构体系。Jana[3]给出了MMT，分析了其拓扑性质及架构有效性，并理论验证了其并行算法的快速性。 Islam[4]提出了OMULT，并与OTIS-Mesh的比较表明，OMULT更具有优势。然而，根据BSN的网络连通性及极大容错性，BSNMOT将会比其他双层树形架构更具有竞争力的架构体系，研究其拓扑性质对网络的分析及网络的设计具有重要的意义。

同时，BSN-MOT作为大规模的互联网络，且根据其优秀拓扑性质，研究其上的并行算法可推动现代并行计算机的实际应用。实际上，近些年，针对大规模交换互联网络的并行算法研究确实也成为了热点。例如，针对OTIS(optical transpose interconnection system)，Sahni等提出了建立在OTIS-Mesh上的矩阵算法[5]，以及基于OTISHypercube和OTIS-Mesh上的BPC排列算法[6,7]；Jana等给出了基于OTIS-Mesh的多项式插值算法[8]；Rajasekaran等研究了OTIS-Mesh上的选择及路由等有效算法[9]；而诸如图形处理[10]、数据求和[11]、k-k排序[12]等OTIS算法也已给出。对于BSN架构，Wei wenhong、Sun liting等也研究了其上的矩阵算法[13,14]，在文献[15]中，Ye等提出基于BSNHypercube的数据广播等算法。本文同样研究了在并行处理中基于BSN-MOT的基本通信及应用操作算法，这些算法可以应用至重要的开发程序，如图像处理、矩阵代数、图论等。

2 基本概念和性质

本文定义BSN-MOT是由2n2个同构的n×n(定义)MOT组成，即在BSN-MOT多处理器系统中，BSN-MOT含有2n4个处理器，它是由2n2个点不相交的同构MOT组成，每个处理器的索引都记为(i, g, p)，其中，i代表部索引，二维布局g(x, y)是组索引，代表了组的位置，p(x, y)是处理器的本地索引，则索引(i,gx,gy,px,py)代表了处于第i部的g(x, y)组的p(x, y)处理器。其中，同一组内的处理器链接是组内链接，而不同部的处理器链接则是组间链接，即第i部组g中的处理器p是与第i部组p中的处理器g连接，也就是(i,gx,gy, px,py)与连接。图1给出了含有32个处理器的BSN-MOT。在图中，小方框代表处理器，大方框则代表处理器组。小方框中的数据对(i, j)指明每组MOT中的本地索引；而大方框外的数据对(a, b)则是每部中的组索引。

2.1 基本定义

定义1 (组内链接)。MOT中的组内链接包含了行树链接及列树链接[16]。

在MOT的每行中，处理器都形成了一颗行树，根节点索引记为(i,gx,gy,px,1)，且在每部中，对任意gx，gy，1≤gx,gy≤n ，P(i,gx,gy,px,py)都直接与P(i,gx,gy,px,2py)及P(i,gx,gy,px,2py+1)（若存在）连接，其中，1≤px,py≤n 。

相似地，在MOT的每列中，处理器都形成了一棵列树，其根节点为P(i,gx,gy,1,py)，且对gx，gy,1≤gx,gy≤n ,P(i,gx,gy,px,py)都直接与P(i,gx,gy,2px,py)及P(i,gx,gy,2px+1,py)(若存在)连接，其中，1≤px,py≤n 。

图2给出了BSN-MOT中单组6×6MOT示例。

定义2 (组间链接)。组间链接定义如下：处理器P(i,gx,gy,px,py)直接与连接。

图1 32处理器的BSN-MOT

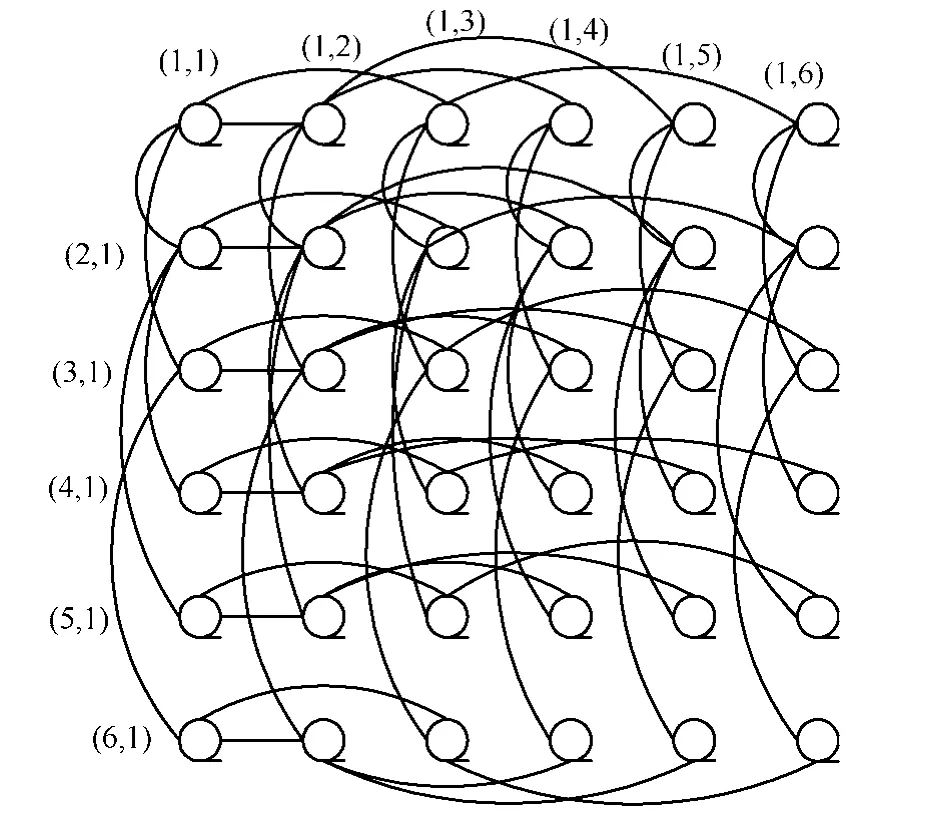
图2 BSN-MOT6中部0中的组g(0,0)

2.2 拓扑性质

2.2.1 最短路径

假设d(u,v)表示MOT中处理器P1到P2的最短路径长度；P1(i1,gx1,gy1,px1,py1)与P2(i2,gx2,gy2,px2,py2)是BSN-MOT中的任意两不同点，则P1到P2的最短路径分下列3种情况构造。

1) 路径只存在组内移动。当且仅当i1=i2，g(x1,y1)=g(x2,y2) ，且p(x1,y1)≠p(x2,y2)，即P1与P2是同部内同组中的不同两点，则在MOT中，从P1到P2的一条最短路径为p1→s1⇒s2→p2，其中s1属于与p1相邻的处理器集合，s2属于与p2相邻的处理器集合。

2) 路径包含偶数个组间移动。当且仅当i1=i2，g(x1,y1)≠g(x2,y2)，且p(x1,y1)≠p(x2,y2)，即P1与P2是同部内不同组的两点。如果组间移动的数量超过2个，则可压缩得到从P1到P2的一条最短路径p1→s1⇒s2→p2，即

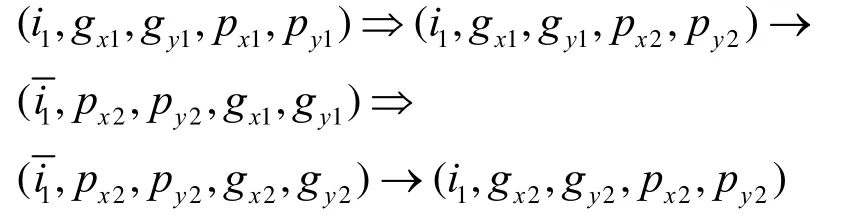
其中，双箭头代表组内移动，单箭头表示组间移动。

3) 路径包含奇数个组间移动。当且仅当i1≠i2，即P1与P2属于不同部的两点。在这种情况下，最短路径必包含一个组间移动，其最短路径为p1→s1⇒s2→p2，即

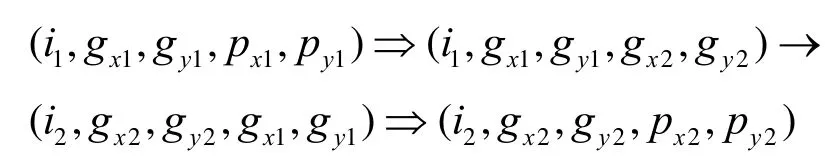
注意的是，如果p(x1,y1)=g(x2,y2)，则

(i1,gx1,gy1,px1,py1)⇒(i1,gx1,gy1,gx2,gy2)为一条空路径；若g(x1,y1)=p(x2,y2)，则(i2,gx2,gy2,gx1,gy1)⇒(i2,gx2,gy2,px2,py2)同为空路径。

从以上情况可以看出，情况1)的最短路径长度为d(p(x1,y1),p(x2,y2))，情况2)和情况3)的最短路径长度则分别为d(p(x1,y1),p(x2,y2))+d(g(x1,y1),g(x2,y2))+2及d(p(x1,y1),g(x2,y2))+d(g(x1,y1),p(x2,y2))+1。

2.2.2 直径

定理1 BSN-MOT的直径为8logn+2。

证明 因BSN-MOT的每组都是一n×n MOT，而直径是指网络图中最大的离径，则BSN-MOT每组的直径为4logn。假设P1与P2各自代表BSN-MOT中任意不同的源节点及目标节点。如果i1≠i2，则两节点可通过一组间链接来连接。如此，可从源节点过渡到一中间节点，即(i1,gx1,gy1,gx2,gy2)，其路由距离即为4logn。而从(i1,gx1,gy1,gx2,gy2)出发，可以通过一组间移动到达(i2,gx2,gy2,gx1,gy1)，之后通过另一组内移动，这样就可到达目标节点P2。通过计算，从源节点到目标节点的最大离径即为8logn+1。然而，通过另一种假想，如果i1=i2，则整个路由过程会通过2个组间移动和2个组内移动来完成，依照这种情况，两节点的最大离径即为8logn+2，因此，BSN-MOT的直径即为8logn+2。

2.2.3 容错直径

假设BSN-MOT的任意源节点与目标节点分别由P1及P2来表示。

倘若i1≠i2，g(x1,y1)≠g(x2,y2) ，则如果容错节点是在源节点所在的同行或同列，那么BSN-MOT的直径将变为8logn+1，其路径即是2.2.1节提及的第3种情况；然而，如果容错节点是其路径上的中间节点(i1,gx1,gy1,gx2,gy2)，其路由路径将变为

BSN-MOT的直径变为8logn+3。

倘若i1=i2，g(x1,y1)≠g(x2,y2) ，而容错节点是在源节点所在的同行或同列时，BSN-MOT的直径仍保持为8logn+2，其路由路径即是2.2.1节提及的第2种情况；相似地，如果容错节点是其路径上的中间节点(i1,gx1,gy1,px2,py2)，则路由将绕过此节点，其路由路径变为

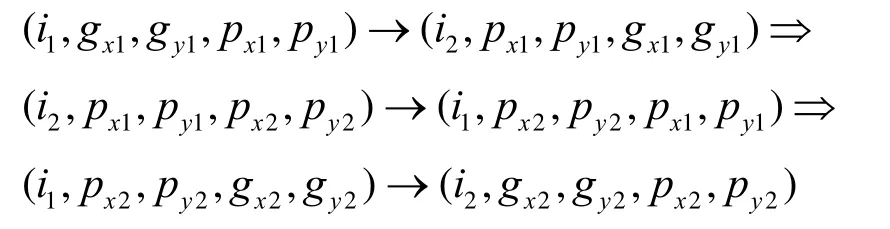
此时，BSN-MOT的直径变为8logn+3。

2.2.4 宽直径

宽直径也是衡量网络容错性的一个重要度量标准，而描述宽直径就需要提到容器的概念。假设G是连通图，u及v是它的节点，则图G中从u到v的一组并行路被称为一(u,v)容器，容器的宽度为其中并行路的条数，容器的长度为其中最长路的长度。某两点间宽度为d的所有容器的最小长度称为这两点间的d-宽距离，所有点对间的d-宽距离的最大值称作是图G的d-宽直径[1]。然而求一般图的宽直径是NP完全难问题，但是参考文献[1]的式(1)～式(8)，本文可推理得到BSN-MOT的宽直径上限不超过3d(MOT)+6，即12logn+6。

3 通信操作算法

本节将提出并行处理中基于BSN-MOT架构的各类基本的通信及应用操作算法，如广播算法、数据求和、矩阵乘积、排序、最短路径路由及多项式求根等，然后通过算法复杂度分析及与其他2种流行树形网络MMT及OMULT的比较来证明BSNMOT是非常快速、有效的网络架构。

3.1 行树广播(Vx, A)

数据广播是并行计算中最基本的通信操作之一。在本算法中，数据vx将被广播至二维BSN-MOT的第x行。此算法描述如下。

step1 赋值v(gx-1)n+px至不同部的首列组的首列处理器，则寄存器A(i,gx,1,px,1)都有了赋值。

step2 通过行树链接，广播寄存器A内的值至同行的其他处理器，如此，第1列组的所有处理器都有了数据值。

step3 对整个网络通过组间链接执行组间移动。这样，不同部的第1列处理器都拥有了一数值。

step4 广播处理器中的数值至同行的其他处理器。

step5 再次执行组间移动。

step6 在step1中广播处理器中的数值至同行的其他处理器。

step7 算法结束。最后，所有x行的处理其都有了数值vx。

图3给出了BSN-MOT3经过行树广播之后的赋值示例。

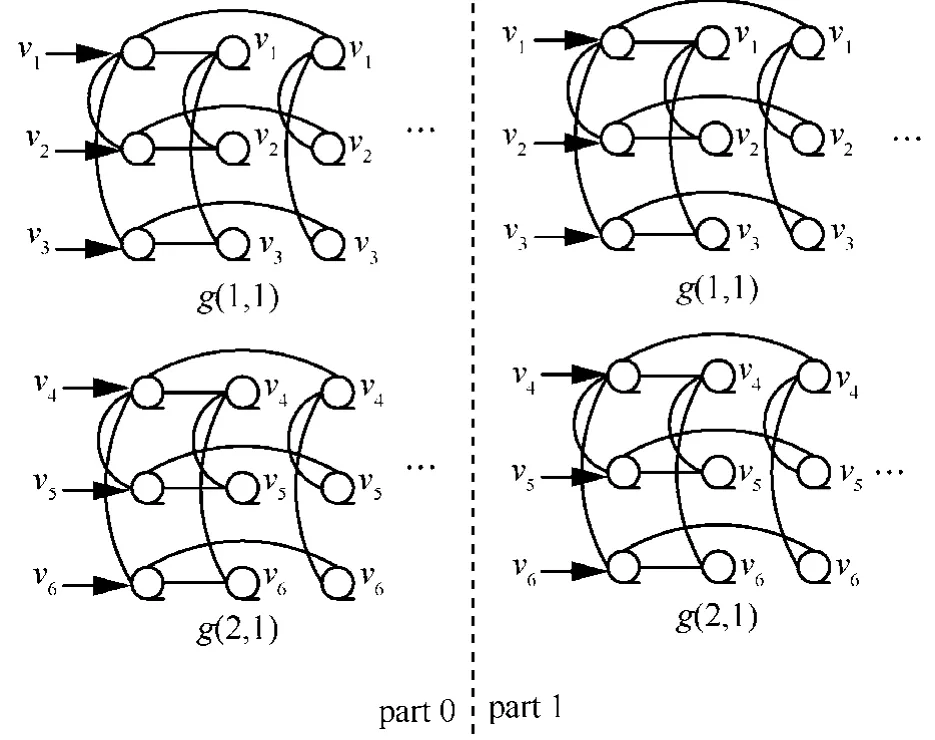
图3 3 3×BSN-MOT中经过行树广播的赋值示例

时间复杂度：从算法可以看到step3及step5各执行一次组间移动，step2通过广播处理器中的数据至本地同行的其他处理器而消耗了logn次组内移动，step4与step2过程相似，同样需要logn次组内移动，由此算法，可得出行树广播的时间复杂度为2logn次组内移动及2次的组间移动。

注意：本文在分析时间复杂度时将以组间移动及组内移动为度量标准，并且，组间移动及组内移动是分开描述的。执行组间移动比执行组内移动需要消耗更大的网络带宽，且组间链接与组内链接在数据传输及等待时间上也是有差异的。

3.2 列树广播(Vy, A)

在列树广播算法中，数据vy将被广播至BSNMOT的第y列。算法描述如下。

step1 赋值v(gy-1)n+py至不同部的第1行组的第1行处理器，则寄存器B(i,1,gy,1,py)都有了赋值。

step2 通过列树链接，广播寄存器B内的值至同列的其他处理器，如此，第1行组的所有处理器都有了相应的值。

step3 对整个网络通过组间链接执行组间移动。这样，不同部的所有第1行处理器都拥有了一数值。

step4 广播处理器中的数值至同列的其他处理器。

step5 再次执行组间移动。

step6 在step1中广播处理器中的数值至同列的其他处理器。

step7 算法结束。最后，所有y列的处理器都有了数值vy。

图4给出了BSN-MOT3在经过列树广播之后的赋值示例。

时间复杂度：与行树广播算法分析相似，此算法的时间复杂度为2logn次组内移动及2次的组间移动。

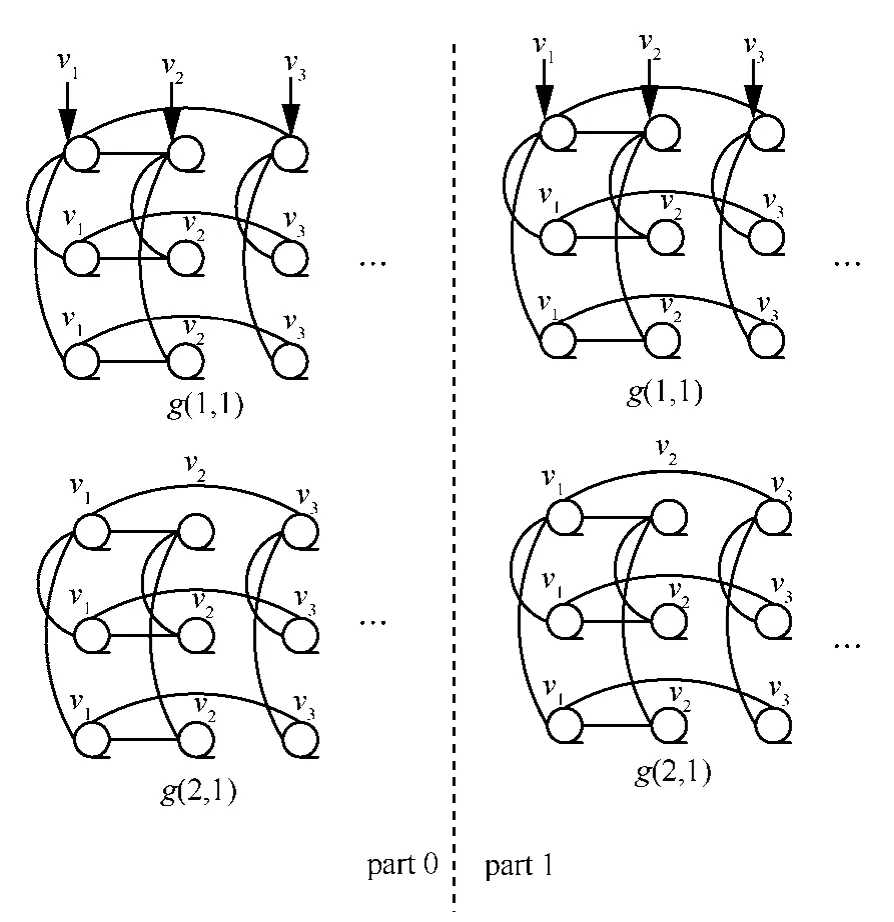
图4 3 3×BSN-MOT中经过列树广播的赋值示例

3.3 单向广播

在此算法中，数据首先被初始放置在一处理器(i,gx,gy,px,py)中，算法执行后，数据将被广播至其他2n4-1个处理器。算法如下。

step1 通过行树链接及列树链接，广播(i,gx,gy,px,py)中的数据至本地组的其他处理器。

step2 对非空组执行一次组间移动。

step4 通过组间链接，广播i内的数据至i部。

step5 算法结束。

时间复杂度：执行完step2，部i中的每组内的一处理器都含有了数据副本，而经过step4，数据在整个BSN-MOT中得到广播。在此算法中，step1及step3各自需要2logn次组内移动，而step2及step4则各需要一次组间移动，算法的时间复杂度为4logn次组内移动及2次组间移动。

3.4 数据求和

在此算法中，每个处理器都含有一数据值，最后，2n4个数据的和值被放置在处理器(0,1,1,1,1)中。算法描述如下。

step1 通过行树及列树链接，对每部中的每组执行本地求和，之后，将和值转至处理器A(i,gx,gy,1,1)。

step2 对含有本地和值的处理器执行组间移动。

step3 分别在处理器A(0,1,1,px,py)及A(1,1,1,px,py)上执行本地求和算法，之后，在i部，将和值移动至A(i,1,1,1,1)。

step4 将处理器A(1,1,1,1,1)上的和值移动至A(0,1,1,1,1)，然后将A(0,1,1,1,1)上的两和值相加。

step5 算法结束。2n4个处理器中的数据的总和值即被存放在处理器(0,1,1,1,1)。

时间复杂度：执行完step2，每部中组g(1,1)的每个处理器都含有一本地和值，在step4中，总的和值被存放在了处理器A(0,1,1,1,1)。此算法的时间复杂度即为4logn次组内移动及2次组间移动。

3.5 矩阵乘法

算法初始，首先利用GRM(group row mapping)[5]方式将2个N2()Nn=阶矩阵A和B映射到含有个处理器的BSN-MOT中，矩阵A被映射到BSN-MOT的0部，矩阵B被映射到1部。图5给出了如何利用GRM将矩阵映射到BSN-MOT的分图示例。在算法中，本文实现BSN-MOT上矩阵A及B的相乘，其乘积即为其中，矩阵第i行j列的元素被映射到组i的第j个处理器。算法如下。

step1 将部1中的B值通过组间链接移至0部。

step2 在部0中，每个处理器都通过行树链接及列树链接将本地组中的A、B值集结。

step3 将集结的B值沿组间链接移至部1中。

step4 将集结的A值也从处理器(0,,)ij移至(1,,)ij。

step5 在部1中，每个处理器都计算其内的A值与B值的对应内积。

step6 算法结束。乘积矩阵在部1中生成。

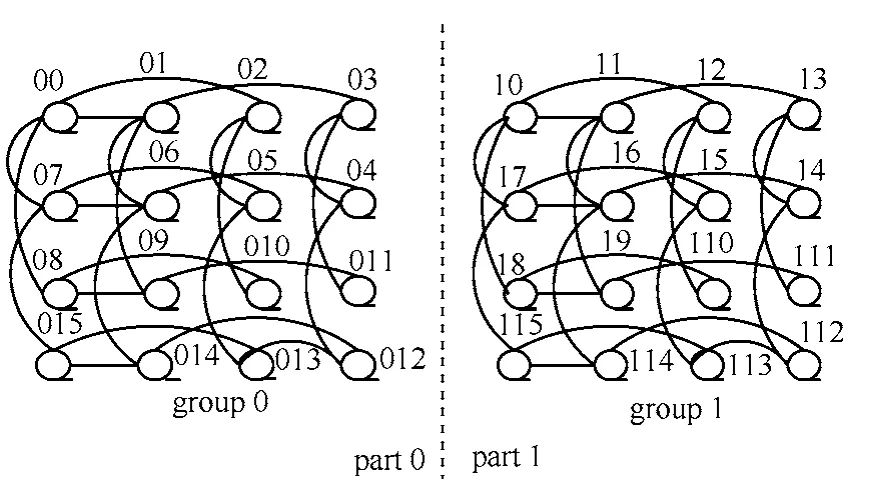
图5 GRM矩阵元素映射至BSN-MOT4的分布示例

由上述算法得知，算法开始时，矩阵元素Aij及Bij被分别放置在处理器(0,i,j)及(1,i,j)中。执行完step1，(0,i,j)含有Aij及Bij；在step2中，每组中的每个处理器都含有矩阵A的第i行值及B的第j列值；执行完step3，部1中每组的处理器都含有B的第j列值。而在step5，乘积矩阵的元素Cij在部1中得出。

时间复杂度：值得说明的是，在step2中，本地组中的所有A值与B值都被集结，此步需要4logn次组内移动。最后，此算法的时间复杂度即为2次的组间移动及4logn+2次的组内移动。

注意：可以利用此映射方式及BSN-MOT计算两向量的乘积，如列向量×行向量，行向量×列向量，或行向量×矩阵以及矩阵×列向量。

3.6 排序

在此，本文对n2个数据元素z0,z1,…,zn2-1进行排序。假设BSN-MOT的每个处理器都含有3个寄存器A、B、C，寄存器A及B用来存储数据元素，C用来存储数据排名。首先，寄存器A的初始赋值如下：(i,gxy,A00)←z(nx+y)，其中，0≤x,y≤n-1。算法如下。

step1 对任意x及y，0≤x,y≤n-1 ，广播(i,gxy,A00)中的值至本地组的其他处理器。

step2 对任意x及y，0≤x,y≤n-1，将(i,gxy,Akl)赋值给(i,gxy,Bkl)。

step3 对任意x，y，k，l，0≤x,y,k,l≤n-1 ，对(i,gxy,Bkl)中的数据执行组间移动。

step4 对任意x，y，k，l，0≤x,y,k,l≤n-1，如果(i,gxy,Akl)≥(i,gxy,Bkl)则(i,gxy,Ckl)=1；反之，(i,gxy,Ckl)=0。

step5 对寄存器C中的数据执行本地组的求和，之后和值寄存在处理器(i,gxy,C00)。

step6 对任意x及y，0≤x,y≤n-1，广播处理器(i,gxy,C00)的数据至本组内的其他处理器。

step7 对任意x，y，k，l，0≤x,y,k,l≤n-1，如果(i,gxy,Ckl)=nk+l+1，对(i,gxy,Akl)及(i,gxy,Ckl)执行组间移动，随后各自在本地组内进行广播。

step8 对任意x，y，k，l，0≤x,y,k,l≤n-1，对(i,gxy,Akl)执行组间移动。

step9 算法结束。

图6给出了数据集{60，45，65，55，23，18，59，78，3}在BSN-MOT3上执行完排序算法后的分布示例。

时间复杂度：可以看出，在step3、step7及step8中各执行了一次组间移动，而step1、step4、step5及step7则各自执行了2logn次组内移动。此算法的时间复杂度则为8logn次组内移动及3次的组间移动。

3.7 最短路径路由

本节提出一种应用在MOT上的基于SPR[2]的新的最短路径路由算法，称之为E-SPR，随后将E-SPR应用在整个BSN-MOT中。

首先，将E-SPR应用在MOT中。本文定义(x,y)为顶点u的二维二进制表示，其中，“x”表示u的行索引，“y”表示u的列索引。对整个MOT，其根节点被标志为(1,1)。对任意的内部节点u，它的左孩子被标记为2u，右孩子被标记为2u+1。接下来便给出从节点u到节点v的最短路径路由算法，其中，u用(x1,y1)表示，v用(x2,y2)表示。在路由过程中，首先遍历行链接的二进制树，直到满足x1=x2，接下来，便开始搜寻列链接的二进制树，直到y1=y2。现在，先以一个行链接的二进制搜索为例：如果x1不是x2的前缀，则将x1移至它的父节点，并将父节点索引标为x1；然而，如果x1是x2的前缀，则将此前缀从x2消除，之后观察x2剩余比特的最左边的一位，如果此比特是1，则将x1移至它的右孩子，并且将右孩子的二进制索引标为x1；若此比特是0，则将x1移至它的左孩子，并将左孩子的索引标为x1。图7就给出了MOT6中从节点u(10,1)到目标节点v(110,101)的最短路由路径。

图6 排序之后寄存器A及C内的数值示例

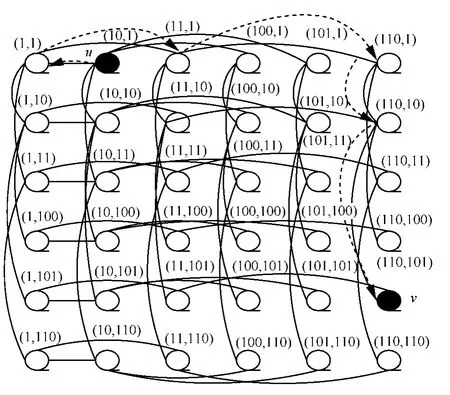
图7 E-SPR: MOT6中从u到v的最短路由路径示例

下一步，本文运用E-SPR至BSN-MOT。假使源节点及目标节点分别为(i1,gx1,gy1,px1,py1)及(i2,gx2,gy2,px2,py2)，则E-SPR算法如下。

step1 在部i1中应用E-SPR至组g(x1,y1)，直到寻到节点(i1,gx1,gy1,gx2,gy2)。

step2 执行组间移动，即可寻到节点(i2,gx2,gy2,gx1,gy1)。

step3 在部i2中再次应用E-SPR至组g(x2,y2)，则目标节点(i2,gx2,gy2,px2,py2)即可遍历到。

step4 算法结束。

时间复杂度：此算法的时间复杂度为8logn次组内移动及1次的组间移动，但是，倘若源节点及目标节点是处于同一部中，则算法的时间复杂度为8logn次的组内移动及2次的组间移动。

3.8 多项式求根

多项式求根是许多实践应用中重要的计算步骤之一，如在并行计算的负载均衡策略中[17]，多项式求根在基于多项式的迭代模型方法中是非常关键的一步。

首先，N次多项式可表示如下

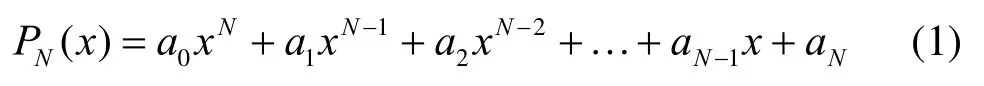
则根据Durand-Kerner迭代模型，其根的表示形式为[18]

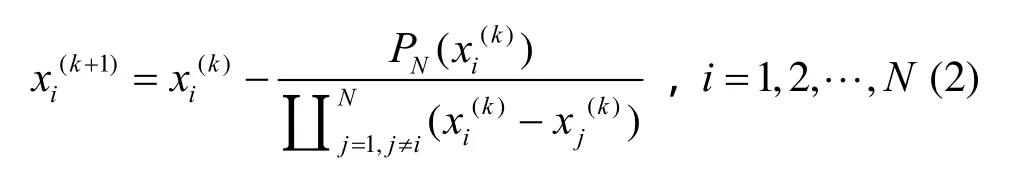
根据上面的公式可以看出，xi(k)表示根的第k个近似值。Jana[8]已经提出了基于OTIS-Mesh的多项式求根算法，在此，提出基于BSN-MOT的多项式求根算法。首先，假设每个处理器都含有4个寄存器，即A、B、C、D。

算法执行如下。

step2 通过行树链接，将寄存器A内的值广播至本地组的其他同行的处理器。

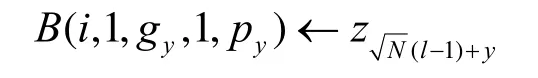
step4 通过列树链接，将寄存器B内的值广播至本地组的其他同列处理器。

step5 对A及B各执行组间移动。

step6 在每组中，广播A值至本地组的同行处理器，同时，广播B值至本地组的同列处理器。

step7 对BSN-MOT的每个处理器：

如果A中的值不等于B中的值，

则A←A-B；

反之，A←1。

step8 在每部中的每组，将同行的所有A值相乘，乘积存储在A(i,gx,gy,px,1)。

step9 对A值执行组间移动。

step10 不同于step8，将部0中第1列组中的所有处于同一行的A值相乘，其乘积放在A(0,gx,1,px,1)。

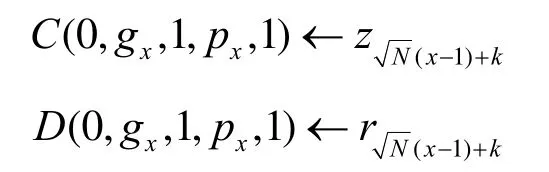
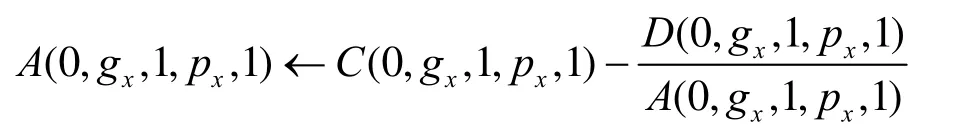
时间复杂度：此算法的时间复杂度即为6logn次组内移动及2次的组间移动。

3.9 BSN-MOT与MMT及OMULT的性能比较

本节将BSN-MOT与另外2种流行的双层树形网络即MMT及OMULT进行比较来说明BSNMOT的快速有效性(在文献[5]中，Jana已经分析了MMT的拓扑性质及架构的有效性；Islam[4]也证明了OMULT的性能优势)。表1列出了3种架构下的各算法的时间复杂度比较。从表中数据可以看出，BSN-MOT是比MMT及OMULT更快速、有效的网络架构，而算法有效的关键点就是利用了BSN特殊的结构体系，以致降低了其通信流量。

4 结束语

基于BSN的一系列的理想特性，诸如扩展性，继承因子网络的正则性、点传递性、Cayley图、哈密尔顿圈及极大容错性等，在并行计算中研究其上的基本通信操作算法是非常有意义的。本文提出一种新型的双层架构BSN-MOT，并研究了其上的一些拓扑性质及基本的通信及应用操作算法，如行、列树广播、数据求和、矩阵相乘、排序及多项式求根等，并理论分析了每种算法的时间复杂度，且通过列表研究给出了BSN-MOT与同为基于树的双重架构MMT及OMULT的各算法的时间复杂度比较。从数据结果可以看出，BSN-MOT是比MMT及OMULT更快速、有效的网络架构。而未来的工作将基于BSN-MOT的各操作算法是否可以延伸至其他BSN进行展开研究。

表1 BSN-MOT、MMT和OMULT的算法时间复杂度比较

[1] 陈卫东,肖文俊. Biswapped网络(BSN)的拓扑性质研究:点对称性和极大容错性[J].计算机学报,2010,33(5): 822-832.CHEN W D, XIAO W J. Topological properties of biswapped networks (BSN): node symmetry and maximal fault tolerance[J]. Chinese Journal of Computers, 2010, 33(5): 822-832.

[2] KEMAL K, FERNANDEZ A. Mesh-connected trees: a bridge between grids and meshes of trees[J]. IEEE Transactions on Parallel and Distributed Systems, 1996, 7(12):1281-1291.

[3] JANA P K. Multi-mesh of trees with its parallel algorithms[J]. Journal of Systems Architecture, 2004, 50(4):193-206.

[4] ISLAM R, AFROZ N, BANDYOPADHYAY S, etal. Computational geometry on optical multi-trees (OMULT) computer system[A].CCCG 2005[C]. 2005.150-154.

[5] WANG C F, SAHNI S. Matrix multiplication on the OTIS-Mesh optoelectronic computer[J]. IEEE Transactions on Computers, 2001,50(7):635-646.

[6] SAHNI S, WANG C. BPC permutations on the OTIS-hypercube optoelectronic computer[J]. Informatica (Ljubljana), 1998,22(3): 263-269.

[7] SAHNI S, WANG C. BPC permutations on the OTIS-mesh optoelectronic computer[A]. Proceedings of the 1997 4th International Conference on Massively Parallel Processing Using Optical Interonnections,MPPOI'97[C]. Montreal, Can,1997.

[8] JANA P K. Polynomial interpolation and polynomial root finding on OTIS-mesh[J]. Parallel Computing, 2006,32(4):301-312.

[9] RAJASEKARAN S, SAHNI S. Randomized routing, selection, and sorting on the OTIS-mesh[J]. IEEE Transactions on Parallel and Distributed Systems, 1998, 9(9):833-840.

[10] WANG C, SAHNI S. Image processing on the OTIS-mesh optoelectronic computer[J]. IEEE Transactions on Parallel and Distributed Systems, 2000,11(2):97-109.

[11] WANG C F, SAHNI S. Basic operations on the OTIS-mesh optoelectronic computer[J]. IEEE Transactions on Parallel and Distributed Systems, 1998,9(12):1226-1236.

[12] OSTERLOH A. Sorting on the OTIS-mesh[A]. Proceedings of the International Parallel Processing Symposium, IPPS[C]. 2000.269-274.

[13] WEI W, XIAO W. Matrix multiplication on the biswapped-mesh network[A]. SNPD 2007: 8th ACIS International Conference on Software Engineering, Artificial Intelligence, Networking, and Parallel/Distributed Computing[C]. Qingdao, China, 2007.

[14] SUN L, TONG C, SU H. New mapping scheme of matrix algorithms on the Biswapped network[J]. Journal of Computational Information Systems, 2013,9(13):5371-5378.

[15] YE H, XIAO W, WU J. Broadcasting on the BSN-hypercube network[A]. 2009 2nd International Conference on Information and Computing Science, ICIC 2009[C]. Manchester, United Kingdom,2009.

[16] CHEN W, CHEN G, HSU D F. Generalized diameters of the mesh of trees[J]. Theory of Computing Systems, 2004,37(4):547-556.

[17] DIEKMANN R, FROMMER A, MONIEN B. Efficient schemes for nearest neighbor load balancing[J]. Parallel Computing, 1999, 25(7):789-812.

[18] FREEMAN T L. Calculating polynomial zeros on a local memory parallel computer[J]. Parallel Computing, 1989,12(3):351-358.