基于Gerschgorin圆盘理论的认知无线电宽带频谱感知

申滨，王舒，黄琼，陈前斌

（重庆邮电大学 移动通信技术重点实验室，重庆 400065）

1 引言

认知无线电(CR, cognitive radio)[1]作为一种新兴的、致力于解决无线电频谱资源匮乏问题的动态接入技术，近年来得到广泛的重视和研究。CR频谱感知面临着很多难以克服的现实技术难题：①无线信道环境复杂，信道衰落和时延现象严重[2]，CR用户在很多时候需要检测信噪比极低的主用户(PU,primary user)信号；②由于PU活动状态的快速变化和高效利用频谱空洞的要求，CR频谱感知一般只能在极短的时间内完成，因而能够获取的频谱观测数据较少，难以实现高性能感知；③CR检测器中的噪声功率具有很大的不确定性[3]。传统的能量检测器[4]在恒虚警概率(CFAP, constant false alarm probability)准则下根据噪声功率设定判决门限，实现结构非常简单，但其性能易受噪声功率不确定影响，并且在低信噪比时检测性能严重不足，因而，很大程度上只能通过引入合作感知来弥补这些缺陷。其他诸如匹配滤波检测和循环平稳特征检测等方法[5]必须依赖于足够多的精确的先验信息，其优良的检测性能才得以实现。

近年来，除了获得广泛研究的窄带频谱感知和合作频谱感知之外，以宽带频谱作为检测目标的感知技术已逐渐成为CR技术研究中新的热点研究方向。文献[6]讨论了CR系统中的多种多载波通信技术并分析了各自的优缺点。宽带频谱感知的任务是通过对宽带授权频段(LFB, licensed frequency band)中各个子频段（或称为子载波、子信道）进行单频段独立检测或多个子频段联合检测，以实现对各个子频段的活动类型分类和忙闲状态辨识。特别地，对于具备OFDM功能的CR系统，其自身的FFT引擎可非常方便地将LFB分解为由若干连续的子频段组成的集合，一旦CR系统判别出仅包含噪声的子频段子集，它们就可被标记到空闲频谱池中，供CR网络中的用户后续分配使用。早期的宽带频谱感知方案一般都比较简单，主要是采用窄带检测器逐个判决各个子载波的状态。由于每次检测时间内只能完成一个子载波状态的判决，因而本质上仍属于窄带检测（或称为串行宽带检测）的范畴。目前，关于宽带频谱感知的研究文献还非常有限。文献[7,8]提出了利用小波变换进行宽带感知，主要依靠估计接收信号功率谱密度的办法来确定宽带频谱中被PU信号占用的子频段和空闲子频段之间的边界。文献[9]提出了OFDM宽带频谱感知的概念并使用最大似然估计方法完成检测。文献[10]以宽带频谱内CR系统吞吐量最大化为优化目标，提出了基于多频带联合检测的宽带频谱感知方法。文献[9,10]的不足之处在于它们都或多或少地需要关于PU信号和噪声功率的先验信息，因而在普遍意义上缺乏灵活度，较难实现。

从宽带频谱感知的最终目标考虑，CR系统需判定LFB上活动PU占用子频带个数及相应位置。基于PU占用子频段集合势(COSS, cardinality of occupied subband set)感知算法从此目标出发，将宽带感知分为两步来进行：判断被占用子频段个数和判定子频段位置。该方法因其对先验信息的依赖程度较低而更适于CR系统。然而，目前基于COSS的感知研究还比较欠缺。WAX和KAILATH最早使用统计学方法提出了基于信息论准则(ITC, information theoretic criteria)的AIC (akaikes information criterion)和MDL (minimum description length)源信号检测方法[11]，主要目的是估计接收信号中所包含的源信号数目。WU H T提出基于Gerschgorin定理的源信号数目估计方法，明显提高了ITC算法的性能[12]。文献[13]在文献[11]的基础上，将传统的ITC算法应用于CR宽带频谱，可以看作是最早通过COSS进行宽带频谱感知的研究。

针对上述研究中存在的问题，本文提出基于Gerschgorin圆盘理论(GDT, Gerschgorin disk theorem)[14]的宽带感知算法。通过将宽带频谱观测数据在Gerschgorin圆盘域上进行噪声圆盘集合和PU信号圆盘集合的分离，来估计空闲子频段集合，从而确认整个LFB中各个子频段的忙闲状态。在对感知协方差矩阵Gerschgorin酉变换(GUT, Gerschgorin unitary transform)处理的基础上，提出了Gerschgorin似然估计算法(GLE, Gerschgorin likelihood estimate algorithm)，并且，提出在不依赖先验信息的情况下，对PU占用子频段(OS, occupied subband)和空闲子频段(IS, idle subband)进行有效识别Gerschgorin圆盘半径迭代算法(GDRI, Gerschgorin disk radii iteration algorithm)。仿真结果表明，基于GDT感知算法在宽带频谱检测中有很大的优越性：GLE明显地提高低信噪比条件下的感知性能；GDRI则在无需先验信息的条件下具备较好的检测性能，且在采样次数较少时检测错误率很低。因此，基于GDT的宽带感知算法适于实际CR系统。

2 宽带感知系统模型

假设CR系统所监测的宽带LFB范围从fs到feHz，且划分为Q个子频段，每个子频段带宽均等于WHz，即满足W=(fe-fs)/Q。PU和CR用户以不同的优先级共享宽带授权频谱资源。M个PU系统独立且互不重叠地工作在LFB中，且总共占用I个子频段(I≤Q)，如图1所示。其中，第m(1≤m≤M)个PU占用子频段集合为mS= {qm,0, qm,0+1,…,qm,1-1,qm,1}，其元素为CR系统子载波所对应的LFB中子频段序号。本文中假设PU系统的数目、PU信号结构及其占用的子频段等信息对于CR系统都完全未知。经CR接收机检测判决之后得到PU占用子频段集合为PU′S，空闲子频段集合0′S。

图1 宽带LFB上PU信号占用子频段模型及检测判决结果示例

宽带CR系统接收到无线电信号经过预处理之后，输出信号经过Q次DFT处理，得到信号频域采样值rq(η)和信号能量值yq，如图2所示。

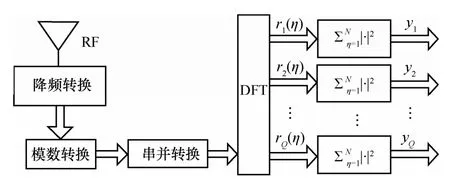
图2 CR接收机接收和处理宽带信号

假设宽带系统中PU发射信号为

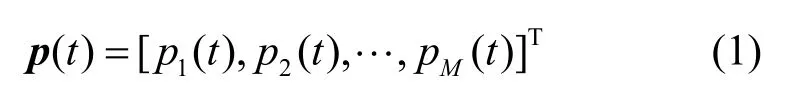
在每次频谱感知观测时间内，CR接收机对接收信号采样N次，tk时刻接收到的时域信号r(tk)表示为

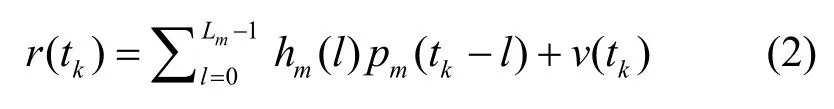
其中，l=0,1,…,Lm-1，hm(l)为第m个PU信号到接收机的第l条多径信道系数，v(tk)为检测器tk时刻的叠加噪声。宽带LFB上子频带的忙闲与否采用二元假设表示，使用Hq,1表示第q个子频带被占用状态，使用Hq,0表示其空闲状态。采样数据经过Q点DFT处理，第η次采样值对应得到的频域信号模型如下

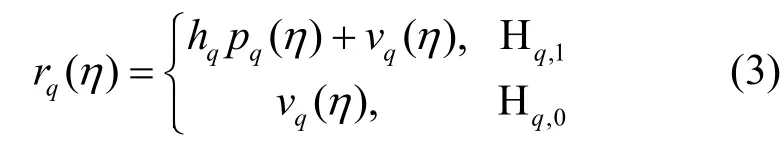
其中，hq、pq(η)和vq(η)分别对应第q个子频段的等效信道增益（q=1,2,…,Q, η=1,2,…,Q），子频段内PU频域信号和噪声信号。更紧凑地，N次采样值对应频域累积信号矩阵可以写为

其中，R为Q×Q矩阵。相应感知协方差矩阵为

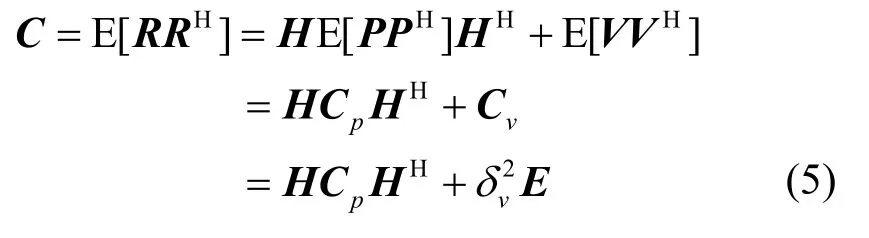
其中，Cp为PU协方差矩阵，Cv为噪声协方差矩阵，δv2为高斯白噪声信号的功率，E为单位矩阵。上标(·)*、(·)T、(·)H分别表示矩阵共轭、转置和Hermitian变换，E[·]表示数学期望。实际中信号采样次数是有限的，基于有限次的采样数据得到的估计协方差矩阵假设为C´。当N→∞时，可得到理想协方差矩阵C为

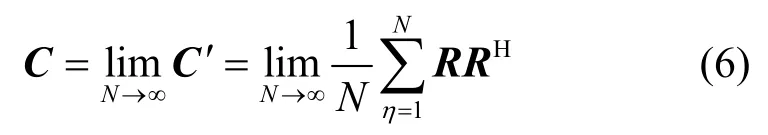
理想的协方差矩阵C有I个较大的特征值并且特征值具有以下性质[15]

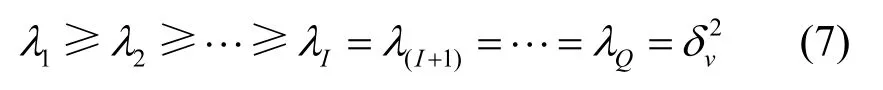
实际中接收机采样次数是有限的并且信号受到不同程度的噪声干扰，因而Schmidt准则[15]不适用，在可用数据受限的情况下，C´对应的特征值为

一般地，宽带能量检测算法可简单地采用基于能量检测的独立子频段门限检测(ISTT, individual sub-band threshold test)判决

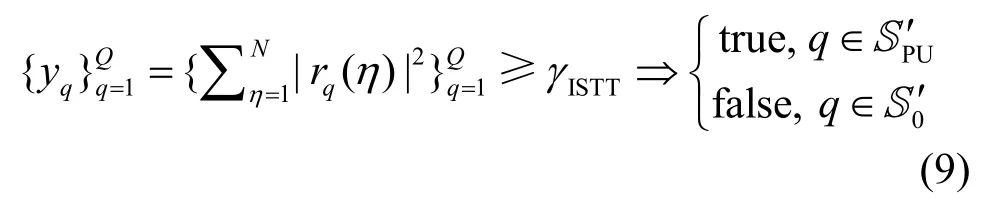
其中，γISTT是判决门限，ISTT判决得到PU占用的子频段集合和空闲子频段集合。能量检测中准确估计噪声功率是获得门限值的关键，但实际中噪声功率的估计存在不确定性，会严重影响能量检测的感知性能。

宽带频谱感知的目的是确定宽带LFB中的IS以供CR机会接入，而确定IS则需要明确的感知判决集合S′0。本文中提出基于Gerschgorin定理的宽带频谱感知算法，基本思想是在GUT的基础上进行判决，首先得到COSS，然后利用子频段对应能量值递进关系确定噪声子载波集合和PU信号子载波集合的边界，最终确定各个子载波归属于集合S′PU或者S′0。具体地，假设信号采样能量值及其对应的子频段序号向量为

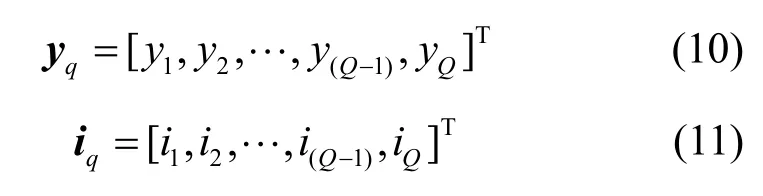
根据能量值递进关系排序得到向量

其中，向量中元素为降序排列

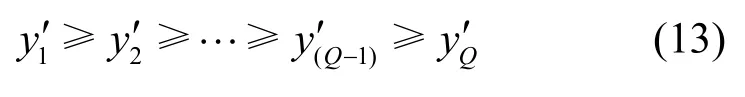
相应能量值对应子频段向量表示为

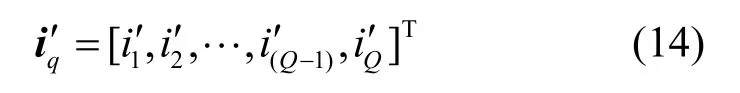
假设运用频谱感知算法得到COSS为I´，则由以上分析得到检测PU占用子频段集合和检测空闲子频段集合分别为

宽带频谱感知的性能评价一般可通过检测率RD和虚警率RFA来衡量

其中，ℜ|·|表示集合的势。P(H0)表示LFB子频段均空闲的概率，P(H1)表示至少有一个子频段被占用的概率，并且，PU并不占用所有LFB子频段，而是合理地工作在部分LFB子频段上。

3 Gerschgorin算法的理论依据

3.1 Gerschgorin定理

对于高阶矩阵一般很难精确地计算其特征值，但是可以通过Gerschgorin定理对特征值的范围进行估计。设A=(aij)是n阶复数矩阵，A∈Cn×n，在复数平面上，满足下面条件的复数x所在区域

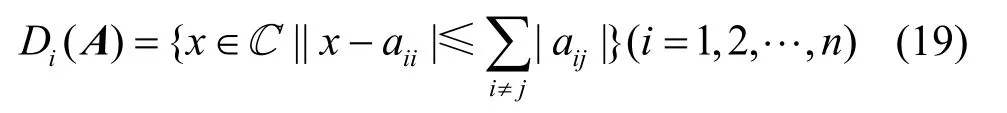
为矩阵A的第i个圆盘，Σi≠j|(aij)|记为Ri(A)，为A的去圆心绝对行和，则矩阵A的第i个圆盘可以写成

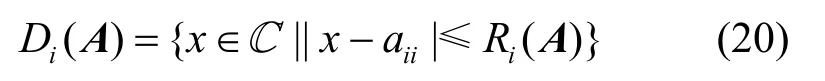
协方差矩阵C是Hermitian矩阵，它的特征值都是实数。根据Gerschgorin定理，矩阵的每一个特征值都位于复平面中相应的圆盘范围内，只要计算出Gerschgorin圆盘的圆心和半径就可以确定实轴上特征值的大致取值范围。但当特征值变化范围很大时，Gerschgorin圆盘半径较大并且各个圆盘的圆心相距较近，会出现圆盘重叠现象，Gerschgorin定理将难以把矩阵各个特征值的可能存在区域（即Gerschgorin圆盘）加以分离。为解决此问题，可利用Gerschgorin酉变换方法来有效分离PU圆盘集合和噪声圆盘集合。

3.2 Gerschgorin酉变换

由于采样协方差矩阵是高阶矩阵，如果直接使用Gerschgorin定理进行判决，会由于严重的圆盘重叠现象而导致较多的错误判决。本文设计一种酉变换方法来有效地分离PU圆盘和噪声圆盘。Gerschgorin酉变换首先将感知协方差矩阵C分块

协方差矩阵C可以表示成

其中，L是由矩阵C的特征向量组成的酉矩阵

λ是由协方差矩阵的特征值组成的对角矩阵

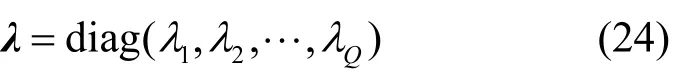
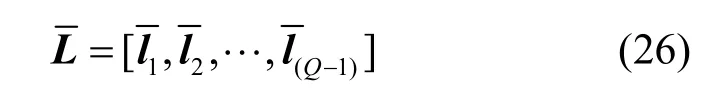
λ是相应的特征值组成的对角矩阵

协方差矩阵C第Q行的前Q-1个元素组成向量¯c可以表示为

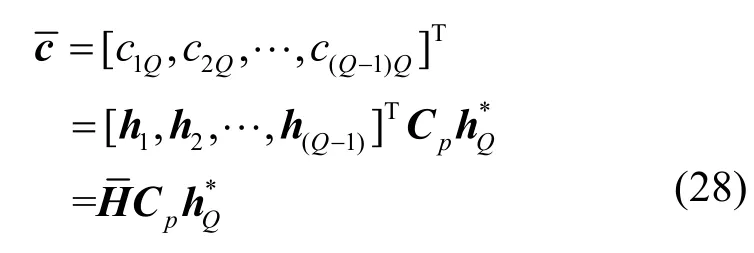
由以上分析可以得到实现GUT的变换矩阵为

协方差矩阵C酉变换之后得到矩阵U

U是C的GUT变换，酉变换得出的Q-1个圆盘圆心和半径，其中半径为零的圆盘是噪声圆盘，剩下的圆盘为PU圆盘，如图3(a)所示。实际中协方差矩阵C´对应的GUT为

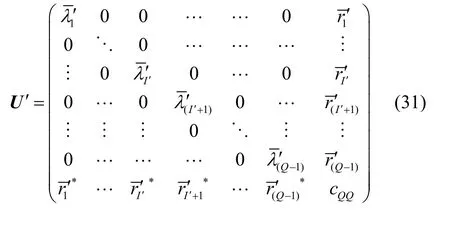
根据酉变换矩阵U'得到的噪声圆盘半径并不全为零，PU圆盘和噪声圆盘的区分并不明显，如图3(b)所示。因此需要设置并调整圆盘半径判决门限来确定门限值，以便区分PU圆盘和噪声圆盘。

图3 Gerschgorin酉变换分离圆盘集合示意

4 基于GDT的宽带频谱感知算法

4.1 基于信息论准则的宽带频谱感知算法

基于ITC的宽带频谱感知算法，首先需要判定协方差矩阵C的类型和接收信号采样值的概率密度函数，由此确定C的秩，接收机采样值rq(1),…,rq(n),…,rq(N)是相互独立的高斯随机向量，根据文献[11]，协方差矩阵C可以表示为

其中，F(ρ)表示秩为 ρ的半正定矩阵，ρ=1,2,…,Q，δ表示未知标量。根据线性代数中的谱定理，用协方差矩阵C(ρ)的特征值 λi和特征向量li表示C(ρ)

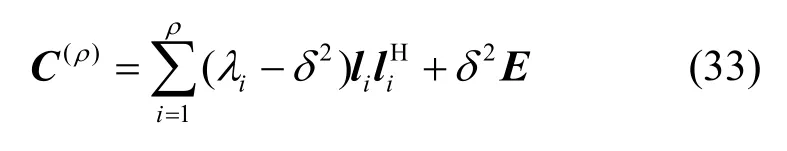
由Schmidt准则可以得到似然比参数向量为

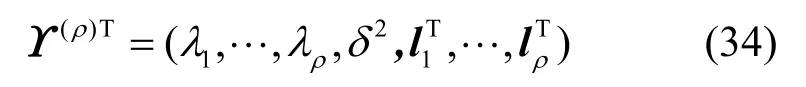
采样值相互独立且服从高斯分布，则联合概率密度函数可以表示为

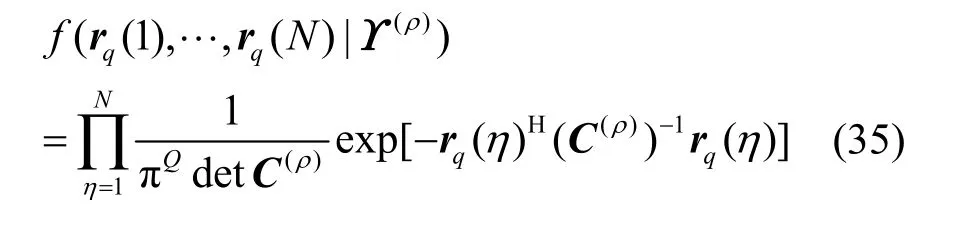
由此推导出AIC和MDL函数表达式分别为

将实际中接收机采样得到的协方差矩阵的特征值代入上述方程得出

当函数取最小值时取得PU占用子频段集合的势COSS，再通过式(10)～式(16)，最终得到空闲子频段。

目前基于ITC检测算法由于其操作仅局限于协方差矩阵的特征值，没有充分地发挥特征向量的作用，在信噪比较小时不能有效地检测信号，因此，在4.2节中将提出一种有效可行的宽带频谱感知算法对其进行改进。

4.2 Gerschgorin似然估计算法

GLE算法是基于酉变换矩阵的似然估计算法，在ITC的基础上充分考虑特征值和特征向量的信息对其进行改进的算法。根据文献[12]，得到似然比方程

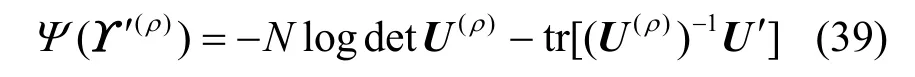
其中，γ´(ρ)为酉变换矩阵U(ρ)的似然比参数向量。将U(ρ)分块得到

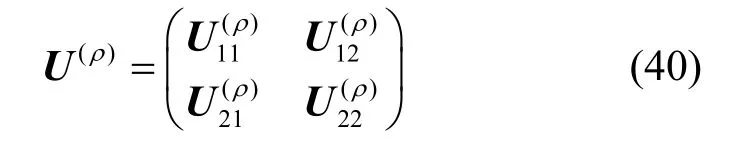
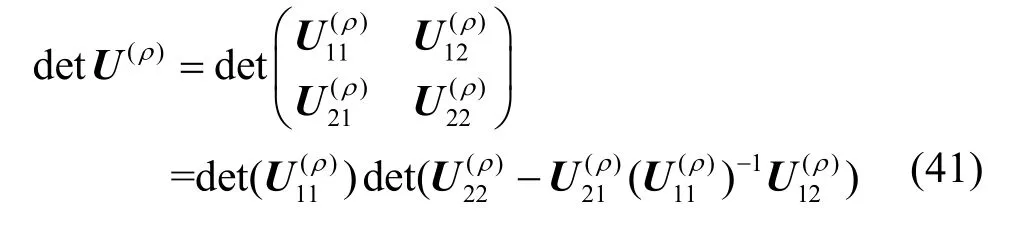
及

由此推导出U(ρ)的行列式为

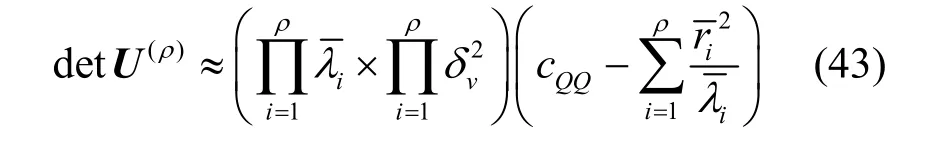
根据以上的推导，给出GAIC和GMDL函数表达式分别为

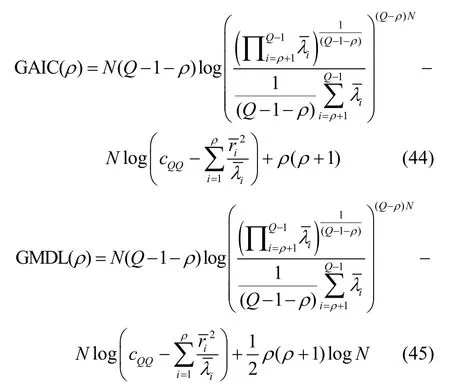
将实际采样矩阵的Gerschgorin酉变换矩阵中得出的圆盘圆心和半径代入上式，可得

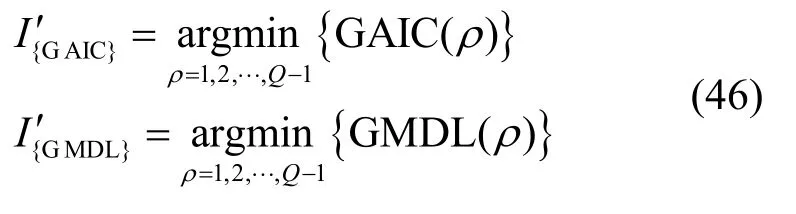
当目标函数取最小值时，就得到了GLE算法的COSS，从而实现对空闲子频段的确定。

虽然GLE算法检测性能很稳定，但只适合于模型单一的高斯随机信号检测，对于非高斯和非白噪声信号这种算法并不适合，因此在应用范围上还是有一定的局限性。

4.3 Gerschgorin圆盘半径迭代算法

如图3所示，只要取得合适的Gerschgorin圆盘半径判决门限就可以有效分离噪声圆盘和PU信号圆盘。GDRI算法是基于特征值的门限判决，与传统门限式判决有很大区别。算法充分考虑协方差矩阵的性质，将半径门限判决与集合势方法相结合，通过对圆盘半径的迭代比较来确定精确的门限值，实现宽带频谱感知不依赖先验信息的目的。

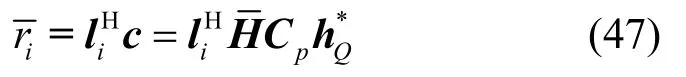
Gerschgorin圆盘半径ri可以表示为

由以上分析定义Gerschgorin圆盘半径迭代GDRI算法判决公式

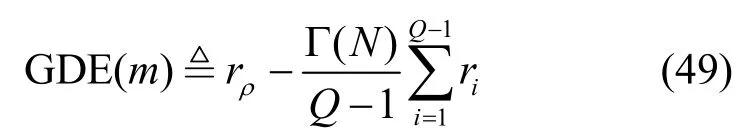
其中，ρ是[1,Q-1]的整数，Γ(N)是关于采样次数N的半径门限系数调节函数，取值为[0,1]，随N增加呈递减趋势[12]。将得到的Gerschgorin圆盘半径代入上式，从 ρ=1开始迭代计算，直到取第一个非正值时取得门限值，得合适的GDRI算法门限。高于GDRI算法半径判决门限的圆盘都被判为PU信号圆盘，反之判为噪声圆盘。当N越大时，噪声Gerschgorin圆盘半径越小，Gerschgorin圆盘半径门限也就越小，因而判决结果就越准确。由此可见GDRI算法只需要对Gerschgorin酉变换得到圆盘半径进行迭代比较得出半径判决门限，算法复杂度较低。

表1为以上所讨论的宽带频谱感知算法的总结，可以看出使用集合势算法和半径门限相结合的GDRI算法更适合宽带频谱感知。

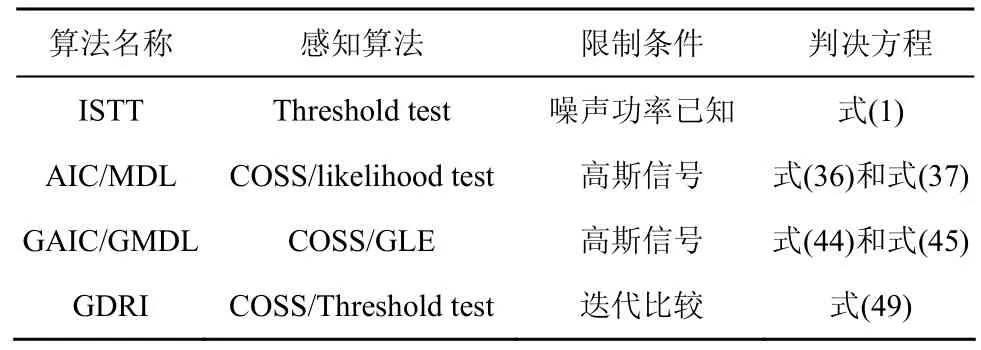
表1 宽带频谱感知算法总结

4.4 改善算法

实际中噪声强度有时会很大，并且一些衰减严重的PU信号会表现出噪声信号的特征，因此，宽带感知算法仅根据COSS得出的PU′S和0′S并不一定精确，需要进一步改进。对此，设计了基于宽带频谱中PU信号所占用频段的连续性特性来改善感知性能的算法，即Gerschgorin频段连续性算法(GSCA,Gerschgorin suband continuity algorithm)，其具体算法步骤如下。

步骤1 首先运行GDRI算法2次，通过调整GDRI半径判决门限的大小得到2个COSS分别为I1'和I2'，并且I1'＜I2'。根据式(10)～式(16)判决得到2个集合分别为PU1′，S和PU2′，S

判决集合中有些元素可能是噪声异动过大而导致PU子频段信号被淹没，从而得到的遗漏判决元素，即OS集合中元素被误判入IS集合；同时，PU1′，S是由相对较大的COSS判决得到，因而虚警率相对较高，相对地，PU2′，S判决对应的检测率较低。

步骤2 考虑宽带系统中OS集合中元素的连续性特性，将判决集合PU1′，S和PU2′，S分类得出

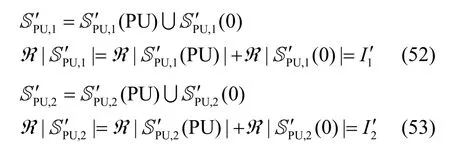
SP′U，1(PU)和SP′U，2(PU)分别由集合SP′U，1和SP′U，2中连续频段子集合的并组成，SP′U，1(0)和SP′U，2(0)是由集合中间断频段子集合的并组成。

步骤3 根据图1逐个查找集合SP′U，1(PU)和SP′U，2(PU)中的所有元素，其中间断频段子集合是噪声干扰强度过大导致的误判，而多个连续的子频段组成的连续频段子集合则为OS集合，将连续子频段元素和间断子频段元素分类，得到具有连续性特性频段元素子集合S1′1,S1′2,…,S1′I′和S2′1,S2′2,…,S2′I′以及间断频段子集合S1′(I′+1),S1′(I′+2),…,S1′(I′′)和S2′(I′+1),S2′(I′+2),…,S2′(I′′)可以得 到分类集合为

步骤4 选取相对较大的COSS能有效地克服较弱的PU信号被噪声淹没的现象，然而在提高检测率的同时也增加了虚警率，要选取较小COSS来除去间断频段子集合以降低虚警率，因此，需要将后者从前者集合中去除。

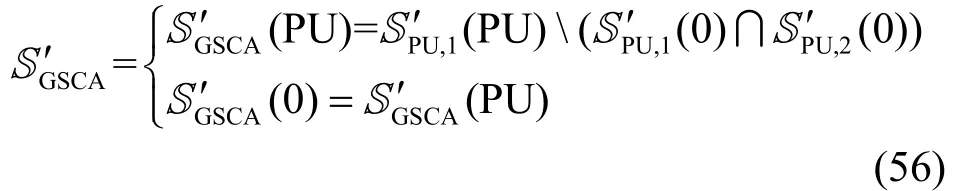
GSCA算法依靠PU占用子频段的COSS来得到最终的检测结果，这样就有效地克服了噪声信号干扰强度过大造成的误判。综合考虑2个集合中信号子载波占用频段的连续性特性，有效地筛选出连续频段元素集合，排除间断频段元素集合，最终提高检测性能。

5 数据仿真及分析

在MATLAB仿真中设定整个宽带频谱监测范围分为1 024个子频段，即Q=1 024，接收机采样次数为N=1 000次。假设宽带频谱上存在2个活动PU，连续占用的子频段的个数分别为256和512，因此，使用PU先验信息，即假设每次感知都在理想已知COSS的条件下进行，就可以获得宽带频谱感知的参考性能线，用于与基于Gerschgorin圆盘集合势的算法的性能作比较。对于ISTT算法需考虑噪声功率作为先验条件，估计噪声功率是噪声功率不确定系数，噪声功率不确定区间为[-ΔdB, ΔdB]，其中，Δ= sup(10lgα)，α 越大能量检测算法的检测性能就越差[16]，仿真中分别取Δ=0，Δ=1给出ISTT性能曲线。

仿真1 在宽带CR系统环境中仿真AIC和MDL算法、GAIC和GMDL算法、GDRI算法以及ISTT算法，并进行性能比较，如图4和图5所示。图中ISTT算法在噪声功率理想已知的情况下即Δ=0时检测性能相对较好，但是在噪声不确定时检测性能很差，虚警率非常高。基于集合势的算法在理想条件下的感知性能Reference曲线，不仅在检测率上非常接近ISTT(A=0)的性能曲线，而且随着信噪比的增加虚警率得到明显的改善，这也是基于集合势算法较传统CFAP检测的优势。基于AIC和MDL算法虽然虚警率极低，但是，在信噪比较小时因检测率过低而无法实现检测PU信号的目的。GLE算法充分考虑特征值和特征向量的信息，检测性能相对稳定，在信噪比较小时仍然能够保持较好的检测性能。GAIC算法虽然检测率较高，但是虚警率也较高。GMDL性能曲线非常接近Reference，检测性能相对稳定。仿真结果表明GLE算法性能明显优于基于ITC感知算法。图中GDRI算法在不需要任何先验信息的情况下检测性能略微超过ISTT算法，检测性能相当稳定，与传统能量检测相比更适合于宽带频谱感知。

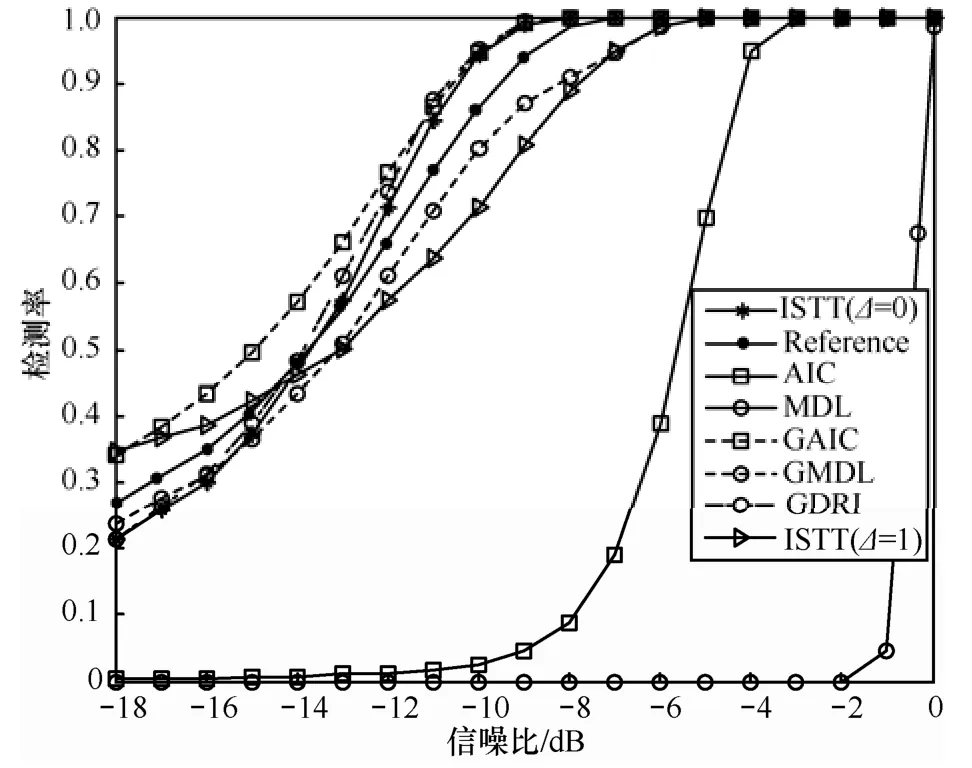
图4 宽带频谱感知算法检测率性能比较

图5 宽带频谱感知算法虚警率性能比较

仿真2 在CR系统环境中，实现不同采样次数条件下的算法性能仿真，如图6和图7所示。仿真中GDRI算法在采样次数较少时检测率相对较低，但随后就快速改善；GMDL算法有相对比较稳定检测性能，最接近基于集合势算法理想条件下感知性能Reference曲线。仿真结果表明了采样次数和先验信息的缺乏对Gerschgorin圆盘感知算法的影响较小，GDRI算法的研究在认知无线电宽带频谱检测中具有实际的意义。

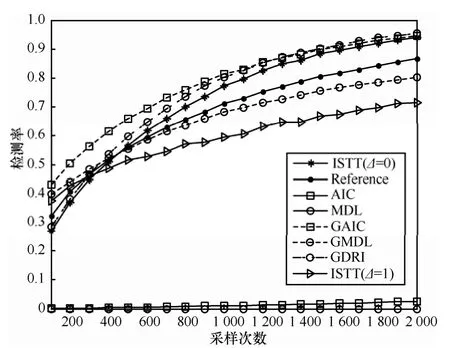
图6 宽带频谱感知算法检测率性能比较

图7 宽带频谱感知算法虚警率性能比较

仿真3 在CR系统环境中，仿真GDRI算法的改进算法GSCA算法。GSCA算法考虑利用PU占用子频段的连续性特性来增强算法的性能，如图8所示，GSCA算法性能明显优于原有GDRI算法的性能，检测率得到了明显的提高，同时虚警率得到了较好的抑制。GSCA算法是在基于集合势算法的基础上，结合实际情况融合了宽带系统PU占用子频段的性质，最终达到提高性能的目的。

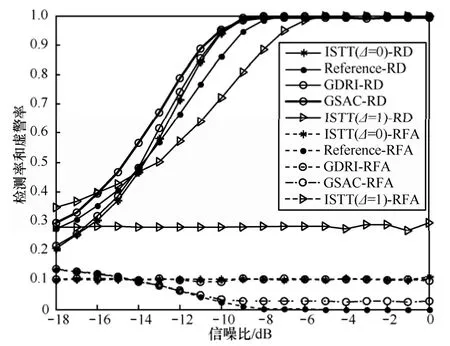
图8 GSCA算法频谱感知性能

6 结束语

本文提出了基于Gerschgorin圆盘理论的宽带频谱感知算法，提出了新型的基于集合势的方法，并在其基础上提出了适合于宽带频谱感知的GLE和GDRI算法。GLE联合考虑特征值和特征向量，将Gerschgorin定理与似然比算法相结合改善了基于信息论准则算法的性能。GDRI算法在不需要先验信息的前提条件下，通过圆盘半径迭代比较确定门限值来判决子频段状态，最终得到较好的检测性能，特别是性能改善算法GSCA充分考虑到宽带系统中PU占用子频段的连续性特性，明显地改善了GDRI算法的检测性能。与现有的各种算法相比，基于Gerschgorin圆盘理论的宽带频谱感知算法体现出较大的优势，可作为现实中具体的算法实现方案加以应用。

[1] HAYKIN S. Cognitive radio: brain-empowered wireless communications[J]. IEEE Journal on Selected Areas in Communications, 2005,23(2): 201-220.

[2] SAHAI A, CABRIC D. Spectrum sensing: fundamental limits and practical challenges[A]. Proc IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks(DySPAN)[C]. Baltimore, 2005.72-82.

[3] SONNENSCHEIN A, FISHMAN P M. Radiometric detection of spread-spectrum signals in noise of uncertain power[J]. IEEE Transactions on Aerospace and Electronic Systems, 1992, 28(3): 654-660.

[4] CABRIC D, TKACHENKO A, BRODERSEN R W. Experimental study of spectrum sensing based on energy detection and network cooperation[J]. ACM Int Workshop on Technology and Policy for Accessing Spectrum[C]. 2006.

[5] CABRIC D, MISHRA S M., BRODERSEN R W. Implementation issues in spectrum sensing for cognitive radios[J]. IEEE Asilomar Conf Signals, Systems and Computers, 2004, 1:772-776.

[6] BOROUJENY B F, KEMPTER R. Multicarrier communication techniques for spectrum sensing and communication in cognitive radios[J].IEEE Communications Magazine, 2008, 46(4): 80-85.

[7] HUR Y. PARK J. WOO W. A wideband analog multi-resolution spectrum sensing technique for cognitive radio systems[A]. Proc IEEE Int Symposium on Circuits and Systems (ISCAS)[C].2006.

[8] TIAN Z, GIANNAKIS, G B. A wavelet approach to wideband spectrum sensing for cognitive radios[J]. Proc 1st Int Conf Cognitive Radio Oriented Wireless Networks and Communications[C]. 2006.

[9] HWANG C H, LAI G L. Spectrum sensing in wideband OFDM cognitive radios[J]. IEEE Transactions on Signal Processing, 2010, 58(2):709-719.

[10] QUAN Z, CUI S G. Optimal multiband joint detection for spectrum sensing in cognitive radio networks[J]. IEEE Trans on Signal Process-ing, 2009,57(3): 1128-1140.

[11] WAX M, KAILATH T. Detection of signals by information theoretic criteria[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1985, 33(2): 387-392.

[12] WU H T, YANG J F. Source number estimation using transformed gerschgorin radii[J]. IEEE Trans on Signal Processing, 1995, 43(6):1325-1333.

[13] LIU S, SHEN J, ZHANG R. Information theoretic criterion based spectrum sensing for cognitive radio[J]. IET Communications, 2008,2(6):753-762.

[14] WILKINSON J H. The Algebraic Eigenvalue Problem[M]. Oxford, U K Clarendon, 1988.

[15] SCHMIDT R O. A Signal Subspace Approach to Multiple Emitter Location and Spectral Estimation[D]. Dissertation, Stanford University,Stanford, 1981.

[16] TANDRA R, SAHAI A. Fundamental limits on detection in low SNR under noise uncertainty[A]. Proc Wireless Com 2005[C]. Maui, HI,2005.464-469.