可靠广播单组传输次数的期望

王开云，李幼平，孔思淇，赵强，马卫东

（1.中国工程物理研究院 计算机应用研究所, 四川 绵阳 621900；2. 中国工程院, 北京 100000；3. 中国工程物理研究院 电子工程研究所, 四川 绵阳 621900）

1 引言

网络和信息服务技术的快速发展，使得访问形式服从幂律分布的点对点传输网络极易发生拥塞，难以满足用户需求，进而推动了数据广播/多播理论和技术的研究。在一对多的信息传播模式中，与单播技术相比，广播能够提供更高的数据传输效率，在数据广播、大文件分发、音视频点播等方面得到了广泛的应用。

常见的可靠广播机制包括轮播、ARQ(automatic repeat-request)广播、HARQ(混合ARQ)广播和网络编码（NC, network coding）广播，后者包含ARQ_NC和数字喷泉码2种方式。在单跳、误码传输环境中，如果被传送的数据只有一个分组，除了HARQ广播外，这些广播机制均简化为单组重传。令M为所有用户正确接收一个分组所需的传输次数，参照文献[1,2]，设它的数学期望为E[M]，它与分组丢失率和用户数有关，是分析可靠广播效率的基础参数。

迄今为止，相关文献基于单组数据重传的多用户接收正确率的离散概率分布函数得出了两类E[M]的解：精确的级数解和用于分析复杂度的近似解。前者可能耗费较多的时间，计算复杂，后者的精度在部分区间相当差。本文在研究了对数函数幂级数部分和与相应的连续概率分布函数期望的基础上，通过将级数解和基于连续概率分布的近似解进行有机组合，得到了计算简单、精度较高、物理意义更加明确的E[M]的近似解析解。

2 相关研究工作

本节简单描述部分文献给出的可靠广播/多播的实现机制，并指出E[M]的研究现状。

Pingali、Towsley和Kurose对3种可靠多播协议进行了深入的分析[1,2]。第一种协议的接收方发送ACK（acknowledgments）消息，差错控制以发送方为主完成；后2种协议中，接收方发送NAK（negative acknowledgments）消息（即时发送和随机延时发送），收方主导差错控制的过程。为了比较3种协议的性能，给出E[M]的3种表达式：无穷级数、有限级数和近似解析解。前2个计算比较复杂，后者除了E[M]非常接近于1的情况外，误差较大。Levine等人[3]将文献[1,2]的协议与基于树（tree-based）和基于环（ring-based）的可靠多播协议进行了比较，得到了基于树可靠多播性能更优的结论。对E[M]的分析仍然是该文的重要内容之一，分析方法与文献[1,2]类似。

当信道比较差的时候（尤其是无线传输情形），ACK和NAK差错控制的效率非常低，就需要应用前向纠错（FEC）技术。目前可靠广播FEC方案主要包括RS码（reed-solomon code）和喷泉码[5～8]，它们将k个分组组成数据块进行编码，生成n(n＞k)个包括纠错冗余的分组发送到接收端，用户只要收到足够多的分组（数量不小于k，喷泉码要求的数量稍多一些），就能完整地恢复整块数据。然而，对于非喷泉码的FEC，当错误分组数超过纠错能力时，还是需要重传，重传次数的分析方法与E[M]类似，只不过是将分组重传的过程换成了分块(包括多个分组)重传，分组丢失率变成了FEC后的分块丢失率。这些文献也没有给出E[M]简单、精度较高的近似解。

还有一些非传统的多播纠错方案。Banerjee[4]提出了一种覆盖网络弹性多播，其基本机制为：在树型多播系统中，收到数据分组的节点，以较小的概率向其他分支叶子节点随机发布该分组数据，如果该节点以前未收到此数据，则纠正错误。此方法的开销和延迟较低，效率较高。Nguyen[9]等人提出了一种基于网络编码的可靠多播方法，发送方采用异或计算(⊕)减少需要错误分组重发的数量。例如，收方1只丢失了a分组，收方2只丢失了b分组，发方仅需发送一个分组a⊕b，收方1通过b⊕(a⊕b)可以恢复a分组，收方2通过a⊕(a⊕b)可以恢复b分组。文献[4,9]的分析中还是没有E[M]的简单、精确近似解。Ghaderi[10]等人对无线网络中网络编码的可靠性增益进行了定量分析，他们采用单组传输次数的期望作为可靠性性能指标，并给出了E[M]极限表达式，它在E[M]为1～10的范围内，除了接收者数量很少的情况外，误差非常明显。

3 符号定义和已有的分析结果

本文研究的问题可描述为：一个发送方负责发送分组数据到多个接收者，传输误码引起的各接收方分组丢失率相同且相互独立，一个单组数据平均经过多少次重复传递，所有接收方才能正确接收到该分组数据。符号的定义如下。

p：收方分组丢失率，各收方分组的丢失是不相关的事件；

R：接收用户的数量；

m：一个分组重传的次数；

M：所有接收用户正确接收一个分组所需的重传次数；

Hn：n阶调和数，n为正整数；

γ：欧拉常数，γ≈0.577 215 664 9。

根据文献[1～3,7～10]，E[M]的分析过程如下。

一个分组经过m次重传后，所有用户正确接收该分组的概率为

这里的m为非负整数，式(1)是一种离散的概率分布函数。

所有接收者均正确接收单个分组数据所需的平均重传次数，即M的数学期望为

式(2)～式(4)的计算量是不可控的，当R很大时，式(4)数值计算难度较大，甚至在计算上是不可行的。鉴于精确公式计算的复杂性，文献[2]和文献[10]给出了下列2种简单的近似公式

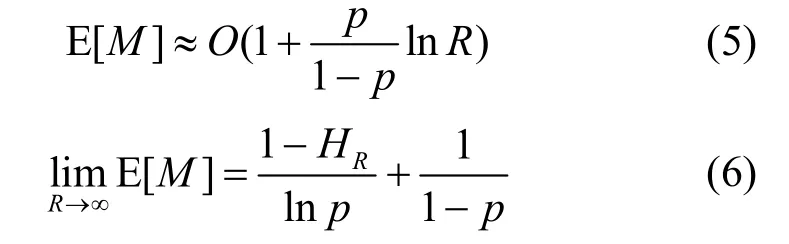
为了分析上述近似公式存在的误差，对R取20，21，22，…，228和229共30种值，对p取46个值，其范围为[10-8, 0.839 67]，后一个值为当前值的1.5倍，总的计算样点数为1 380个，本文后面在检验其他E[M]近似公式的精度时，都将采用这里的实验方案。式(5)和式(6)与式(3)的1 380样点的平均绝对误差分别为1.32和0.306。图1和2给出了式(5)和式(6)误差分布的情况，E3[M]表示式(3)的计算值。计算数据按式(3)结果从小到大进行了排序，式(3)的计算精度为10-10。显然，简单的式(5)和式(6)用于计算E[M]的下限和上限尚可，但用作它的近似式，则精度明显不足。

图1 式(5)的误差分布

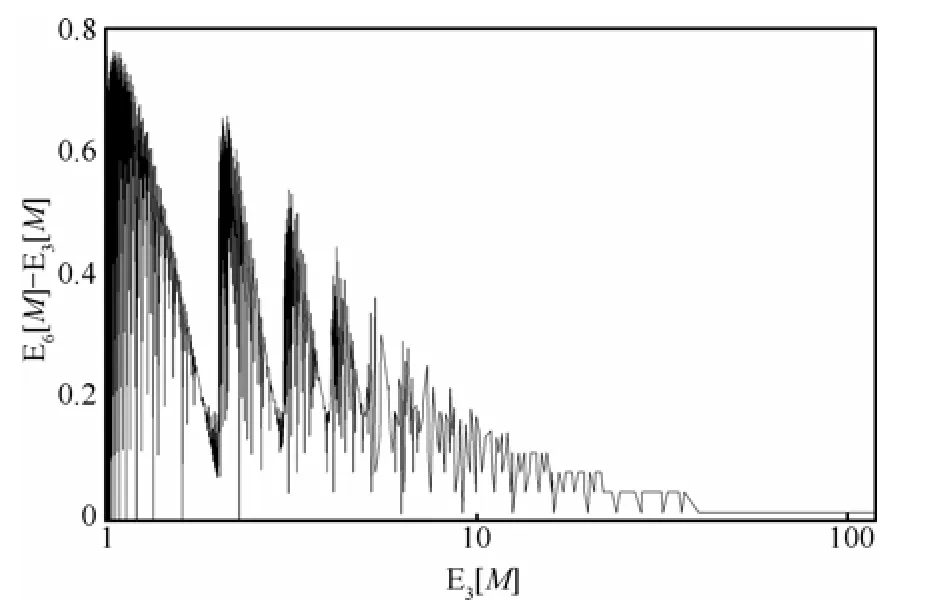
图2 式(6)的误差分布

4 基于连续概率分布的E[M]近似式及其物理意义分析

式(1)是一个离散的概率分布函数，在计算E[M]时，可以用一个连续概率分布函数

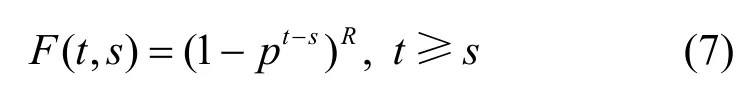
将式(2)的级数计算近似等效为积分计算

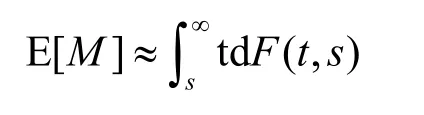
其中，t是连续值的重传次数，s是分布函数的平移量。图3给出了p=0.2，R=5时不同s值的概率分布，其中，F(int(t)，0)与式(1)的离散概率分布相同，图中各分布曲线的左边的面积为相应的期望值。将连续分布函数(1-pt-s)n在区间a≤t≤b的期望（附录B的式(16)）代入式(7)可得

由图3可知，s=0、s=1和s=0.5时式(8)的计算值分别相当于E[M]的下限、上限和近似值，这3种情况与式(3)的1 380样点的平均绝对误差分别为0.536、0.464和0.138。前2种情况的精度优于式(5)，后一种优于式(5)和式(6)。为保证E[M]的计算结果不小于1，s=0.5的式(8)可修改如下

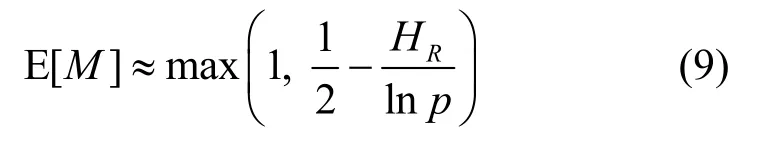
它与式(3)的1 380样点的平均绝对误差为0.091 1，图4给出了式(9)与式(3)的误差分布。

式(3)是一个无穷级数表达式，虽然其计算结果是精确的，但从公式结构来看，只能定性地表明E[M]是p和R的单调增长函数。在此基础上，式(5)和式(6)明确了E[M]与R的关系：当p不变的情况下，若不考虑常数项，E[M]与lnR成正比(lnR是式(6) HR的核心部分)。考虑到所需的前提条件，这种关系是半定量的。式(9)则进一步明确了E[M]与p的半定量关系：若不考虑常数项，E[M]与lnR成正比，与lnp-1成反比，或者说E[M]是以p-1为底的R的对数函数。式(9)的精度明显高于式(5)和式(6)，收敛速度更快，故该式展现变量之间的关系，更接近E[M]的本质。

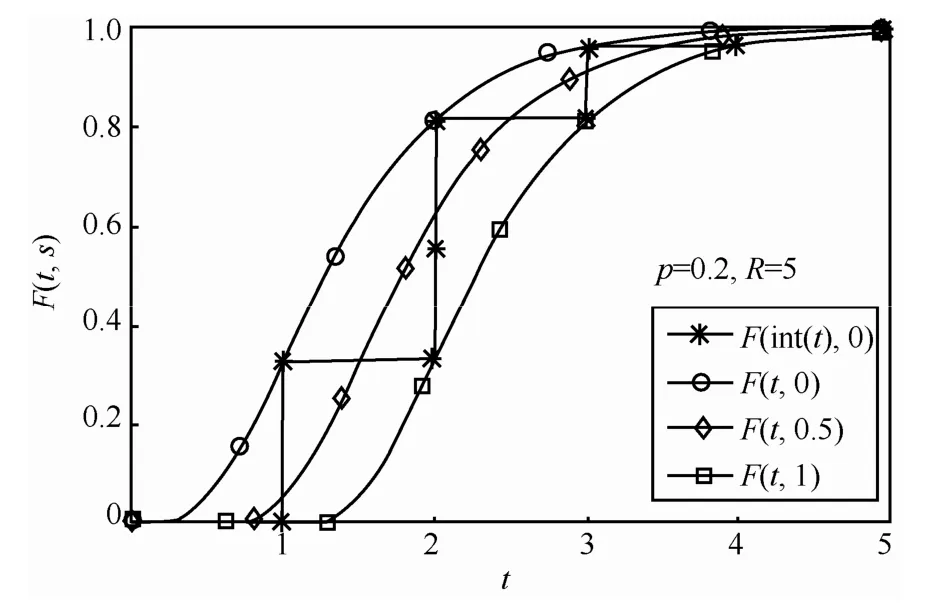
图3 3种s值的连续概率分布和离散概率分布

图4 式(9)的误差分布

5 高精度的E[M]近似表达式

当E[M]比较小时，如果用式(9)取代式(3)仍然存在比较明显的相对误差。通过观察可以发现，在限定结果误差的条件下，如果E[M]较小，式(2)一般仅需要计算前几项的和，即可满足精度要求，计算量并不大；若E[M]较大，采用式(9)能够获得符合精度要求的计算结果。因此，将基于离散分布和连续分布的E[M]计算方法结合在一起，可以获得计算简单、精度较高的E[M]表达式

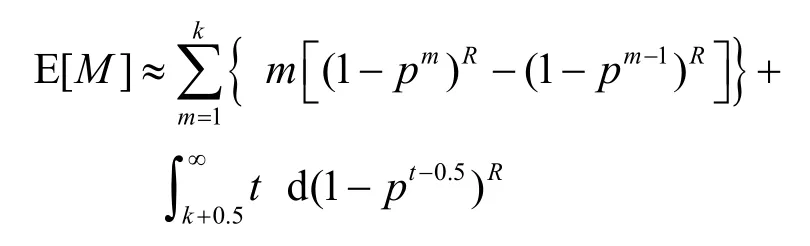
将附录B中的式(16)代入式(9)，并进行多项式合并，可得(推导过程参见附录C)

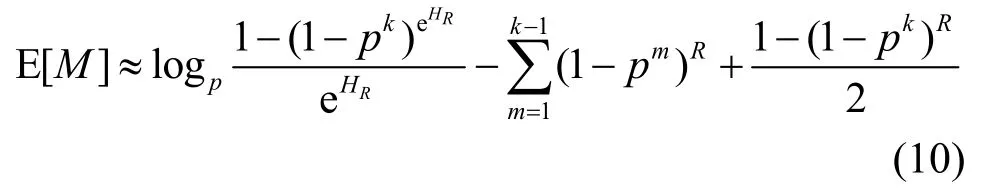
对于k为1到6的情形，式(10)与式(3)1 380样点的平均绝对误差分别为0.071 1、0.021 1、0.009 11、0.005 04、0.003 26和0.002 41。随着k的增加，精度改善的幅度越来越小，故未列出k更大时的结果。在计算分析过程发现，将上式最后的指数项由R调整为exp(HR)，可使这6种情形的误差分别降低到0.059 5、0.015、0.005 46、0.002 55、0.001 47和0.001 02。综合考虑表达式的复杂性和计算精度，选用k=3时的式(10)作为E[M]的高精度近似式

图5给出了式(11)与式(3)的误差分布。为便于与式(6)的精度进行直观的比较，图5还列出了式(6)与式(3)的误差分布。导致式(11)存在误差的主要原因有2个，k的取值不够大，近似处理采用的式(16)本身就存在误差。在本文给定的实验参数条件下，式(11)尽管没有完全消除误差，但其平均精度比式(5)提高了接近3个量级，比式(6)提高了接近2个量级，与式(3)相比，计算更简单。

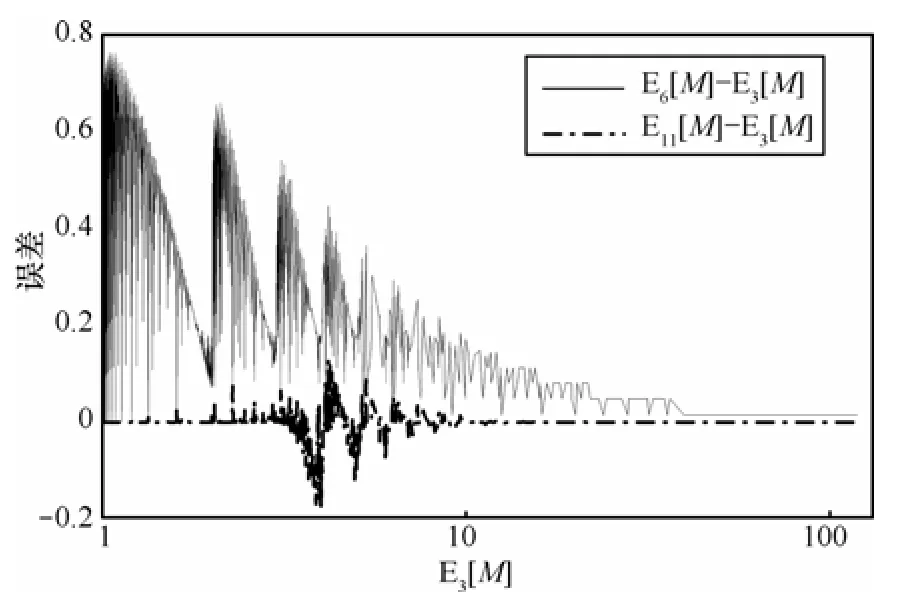
图5 式(11)和式(6)的误差分布

6 结束语

在可靠广播/多播理论中，求解单组数据重传次数的数学期望是一个比较重要的问题。本文通过概率分布函数的连续化近似处理，获得了精度优于已有文献的近似公式，其物理解释更加明确。在此基础上，将它与已有的无穷级数解相结合，得到了一个高精度的近似公式，能够帮助广播/多播系统更加精确地控制单组数据的播发次数，既避免接收不完整，又避免过分冗余，进而提高系统的效率。

本研究并未限定是否存在回传信道。因此，导出的E[M]表达式，既适用于纯单向的广播传输，也可用于双向网络的ARQ广播/多播模式。

附录A 对数函数幂级数部分和的估计

当01p＜≤时，对数函数lnp可展开为如下形式的幂级数

其中，n为正整数，rn(p)为余项，应该满足下列4个条件：

据此可构造一种rn(p)的表达式

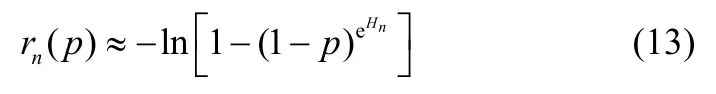
由式(12)和式(13)可得，对数函数幂级数部分和的近似式为

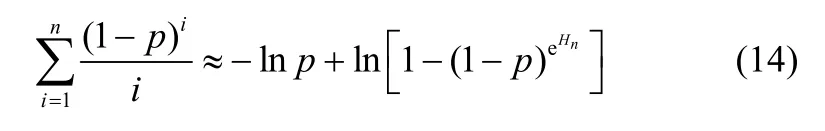
为了检验上述近似带来的误差情况，分别定义

图6 对数函数幂级数部分和近似式的误差分布

附录B 连续分布函数(1-pt-s)n 在区间a≤t≤b的期望

设(1-pt-s)n是随机变量ξ的分布函数。其中，0≤p≤1，n为正整数，a≤t≤b，s≥0，a≥s。随机变量ξ在区间a≤t≤b的期望为

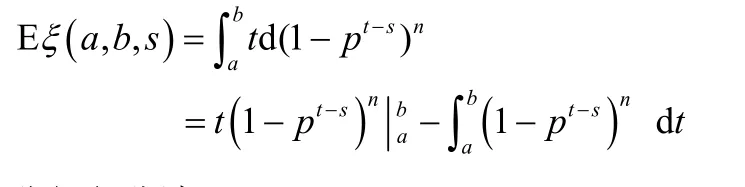
分部积分法

令x=pt-s，则

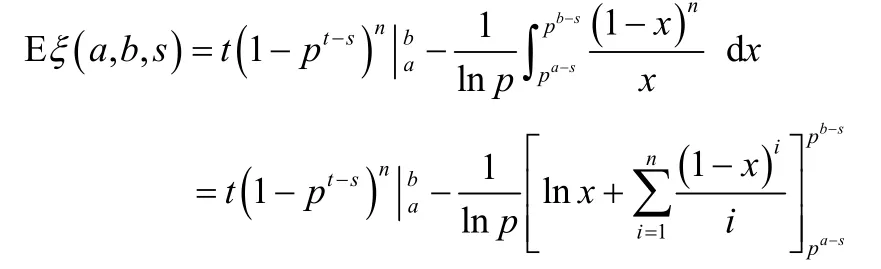
积分逐级降阶

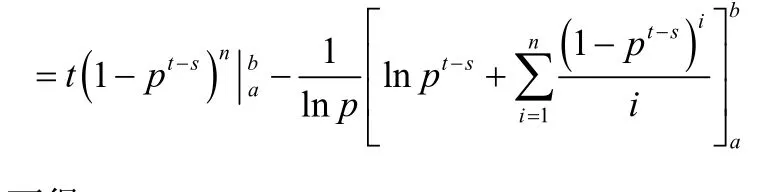
由式(14)可得

附录C 式(10)推导过程

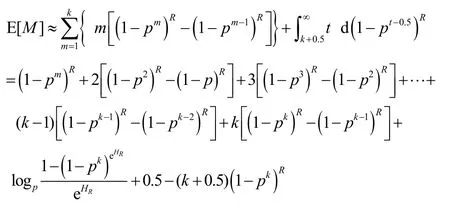
[1] PINGALI S, KUROSE J F, TOWSLEY D. A comparison of sender-initiated and receiver-initiated reliable multicast protocols[A].Sigmetrics’94[C]. New York, USA, 1994. 221-230.

[2] TOWSLEY D, KUROSE J, PINGALI S. A comparison of sender-initiated and receiver-initiated reliable multicast protocols[J]. IEEE Selected Areas in Communications, 1997, 15(3):398-406.

[3] LEVINE B N, GARCIA-LUNA-ACCEVES J J. A comparison of reliable multicast protocols[J]. Multimedia Systems, 1998, 6(5): 334-348.

[4] BANERJEE S, LEE S, BHATTACHARJEE B, etal. Resilient multicast using overlays[J]. IEEE/ACM Transaction on Networking, 2006,14(2): 237-248.

[5] PELTOTALO J, PELTOTALO S, HARJU J. Analysis of the flute data carousel[A].Proceedings of EUNICE Summer School 2005[C]. Colmenarejo, Spain, 2005.138-142.

[6] LUBY M, WATSON M, GASIBA T, etal. Raptor codes for reliable download delivery in wireless broadcast systems[A]. CCNC'06[C].2005.192-197.

[7] 姜博,曹志刚,晏坚.PLFEC 可靠多播解决方案分组长度研究[J].清华大学学报（自然科学版）, 2008,48(4): 567-570.JIANG B, CAO Z G, YAN J. Packet lengths of PLFEC-based reliable multicast solutions[J]. Journal of Tsinghua University, 2008, 48(4):567-570.

[8] 祝峰, 武玲霜, 谷源涛.可靠多播方案的最佳有效负载长度研究[J].通信学报, 2011, 32(6) :101-106.ZHU F, WU L S, GU Y T. Optimial payload lengths of reliable multicast schemes[J]. Journal on Communications, 2011, 32(6):101-106.

[9] NGUYEN D, TRAN T, NGUYEN T, etal. Wireless broadcast using network coding[J]. IEEE Transactions on Vehicular Technology, 2009,58(2): 914-925.

[10] GHADERI M, TOWSLEY D, KUROSE J. Reliability gain of network coding in lossy wireless networks[A]. INFOCOM 2008, Phoenix[C].AZ:IEEE Press, 2008. 2171-2179.