混沌遗传算法在高层结构风振控制优化中的应用研究

张 雷， 张永山， 莊初立， 汪大洋， 蔡长青

(广州大学 土木工程学院， 广州 510006）

0 引言

近年来国内外学者对高层结构的风振控制优化问题进行了一系列研究[1-5]， 结果表明对结构的减振装置进行参数优化可以改善结构在风振中的安全性和舒适性， 文献[6]对主动、 混合和半主动控制装置的参数进行了优化； 文献[7]对被动控制装置的布置位置进行了优化； 文献[8]采用SGA 算法对采用被动控制装置的高层结构进行了参数优化， 文献[9]将CGA 引入了结构优化设计中。 目前高层结构风振控制优化研究采用的方法有迭代法[10]和简单遗传算法（SGA）等。 本文将混沌遗传算法理论引入高层结构风振控制的参数优化领域， 利用Matlab 语言编制了CGA、 SGA、 迭代法和均匀布置的优化程序， 并对九个结构进行了优化运算，分析了各种算法的计算效率和风振响应， 为高层减振结构体系的参数优化和设计提供新思路。

1 基于CGA 算法的风振控制优化

本文采用黏弹性阻尼器来减小高层结构的风致振动响应进行， 黏弹性阻尼器的总等效阻尼系数大小可以表征阻尼器的数量， 在相等的总阻尼情况下结构的风致振动响应越小， 说明等效阻尼系数分布越合理。 混沌遗传算法理论[11]是一种将混沌优化算法和简单遗传算法（SGA）结合起来的混合优化算法， 它兼具混沌优化算法的遍历性、 局部寻优等优点与简单遗传算法[12]的强大搜索能力。 采用CGA 算法对结构楼层间的等效阻尼系数进行参数优化就是以结构的风致振动响应作为优化目标，用CGA 算法在解空间中找出令目标函数取得最小的等效阻尼系数分布方案。 其运算步骤如下：

（1）确定个体的编码方式， 目前采用比较广泛的是二进制编码， 本文也采用这种方式。

（2）采用适合的目标函数值作为CGA 算法的适应度函数对个体进行评价， 本文采用频域法计算出结构顶层位移的均方差作为适应度函数， 其计算方法如下：

式（1）中Sui（ω）为位移反应的自功率谱密度函数，为广义脉动风荷载自功率谱密度函数， φij为结构第j 层受单位荷载在第i 层引起的位移， Hj（ω）为j 振型的传递函数如式（2）， ω 为风荷载的频率， ωj为j 振型的圆频率， ξj为结构第j 阶振型阻尼比。

（3）基于Logistic 映射生成混沌初始群体。 其方法是先设定优化变量xi的取值范围[ai， bi]、 群体规模m、 混沌算子中的吸引子μi， 根据式（3）生成混沌变量：

式（3）中， i 为混沌变量的序号， i=1， …， r， r 是变量的维数； k 为种群序号， k=0， 1， …， m； ζi为混沌变量， 0≤ζi≤1。 令k=0， μi=4 给ζi赋r个微小差异的值， 得到r个混沌变量ζi(1)(i=1， …， r)， 依次取k=0， 1， …， m， 可得m个初始群体的混沌变量， 最后将混沌变量映射到优化变量的区域。

（4）通过选择、 交叉和变异三种遗传算子，对个体进行遗传操作形成新的群体。

（5）当新群体的适应度满足式（4）所示的条件时， 将当前群体的优化变量映射到区间[0， 1]上，并根据式（5）生成新的个体， 可得

式（4）、（5）中， Ymax为新群体适应度最值是新群体适应度均值； ε∈（0，1）是混沌扰动的开关参数为扰动后形成的混沌向量为当前最优解映射到区间[0，1]上的混沌向量；式（6）中， n 为迭代次数， ω 为一整数， α 值随着迭代次数的增加而变小。

（6）重复以上步骤直至求出最优解。 CGA 算法的流程如图1 所示。

图1 CGA 算法的计算流程图Fig.1 Calculation process of CGA

2 分析模型

本文取三组共9个钢框架结构模型作为算例，结构模型的刚度从下往上递减， 每隔五层产生一次变化， 刚度变化控制在30%以下来避免结构出现薄弱层。 风荷载来流方向与结构表面垂直， 基本风压取0.85 kN/m2（对应风速分别为36.9 m/s），场地类别为D 类， 保证系数取2.2， 针对Davenport 风速谱采用频域法计算风振响应。 用剪切型黏弹性阻尼器进行风振控制， 根据Kelvin 模型各层黏弹性阻尼器的等效阻尼系数大小可以表征各层布置的阻尼器个数。 结构的动力特性及黏弹性阻尼器的总等效阻尼系数如表1， CGA 算法和SGA 算法参数如表2。 目前阻尼器的分布方式有均匀布置、 迭代布置和采用SGA 算法进行布置等方式， 本文采用CGA 算法对高层结构风振控制进行优化， 用CGA 工况与无控、 均布、 迭代和SGA 工况进行对比， 以此研究CGA 工况的计算效率和减振效果。

表1 结构基本参数Table 1 The basic parameters of structure

表2 遗传算法基本参数Table 2 The basic parameters of Genetic algorithm

3 算法效率对比

本文采用“平均截止代数”[13]和运算时间两个指标来研究CGA 算法的计算效率， 平均截止代数定义如式（7）

式（7）中S 为遗传策略； Ti为第i 次独立运行时的截止代数， N 为独立运行次数； pi=Ci/N， (0≤pi≤1)， Ci为Ti所对应的统计频数。 平均截止代数越小， 则算法收敛速度越快。

表3 为各个结构采用SGA 算法和CGA 算法的平均截止代数对比。 从中可以看出， CGA 算法的收敛速度比SGA 提高了20%~29%。

表3 算法的平均截止代数（代）Table 3 The average truncated generation of algorithm

表4 为各算法的运算时间， 从中看出均布的运算时间较短， 迭代次之， 而CGA 与SGA 运算时间较长， CGA 相比SGA 运算时间缩短了24%~34%， 但是均布和迭代工况的风致振动响应比CGA 和SGA 大， 具体请见下文的结构风致振动响应分析。

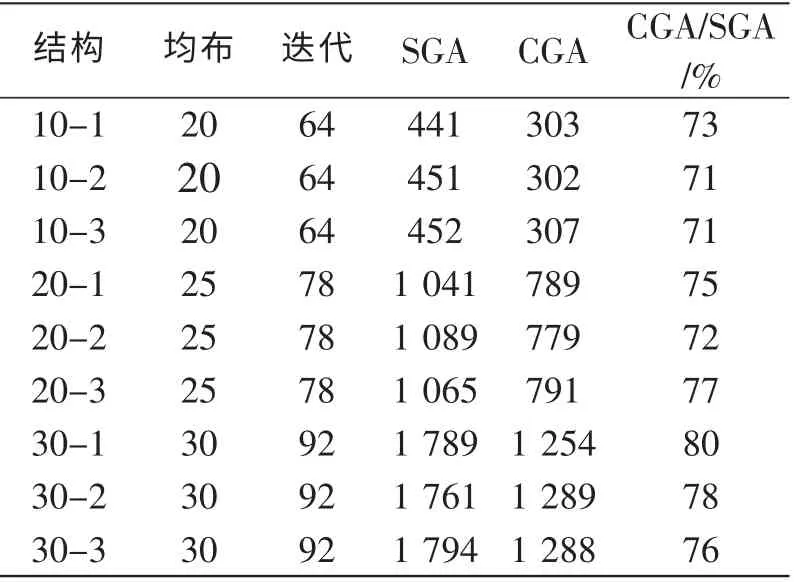
表4 程序的运算时间（s）Table 3 The running time of program

4 风致振动响应分析

表5 为各个结构在各个工况下的附加阻尼比[14]，附加阻尼比是指黏弹性阻尼器附加给结构的阻尼比。 图2 为结构各层的等效阻尼系数分布和加速度响应（限于篇幅仅列出结构10-1、 20-1 和30-3）。 从中看出： ①CGA 和SGA 的附加阻尼比最大， 超出均布最高达61%， 超出迭代法最高达22%； ②SGA 和CGA 的附加阻尼比一致， 原因是CGA 和SGA 都在规定的截止代数之内收敛于最优的等效阻尼系数分布方案， 所以CGA 和SGA 的附加阻尼比和风振响应也是相同的（为便于作图本文仅列出CGA 的结构响应和等效阻尼系数分布）；③CGA 工况的等效阻尼系数分布在中下层位置且从下往上递减。

表5 结构的附加阻尼比Table 5 The additional damping ratio of structure

图2 结构的等效阻尼系数分布Fig.2 The distribution of equivalent damping coefficient of structure

各结构的振动响应如表6 所示。 从中可以看出各工况中CGA 的风致振动响应响应最小， 且CGA 工况对加速度响应的控制优化效果比顶层位移和最大层间位移角要好。 比如CGA 的顶层加速度比均布最高减小了14%， 比迭代最高减小了12%； CGA 的顶层位移比均布减小12%左右， 比迭代减小了8%左右； CGA 的最大层间位移角比均布最高减小了14%， 比迭代减小8%左右。 之所以出现上述现象是因为采用CGA 算法进行风振控制优化时是以结构的加速度响应作为控制目标， 而均布工况和迭代工况并未以加速度响应作为控制目标。

表6 结构的振动响应Table 6 The vibration response of structure

5 结论

本文将混沌遗传算法引入高层结构的风振控制优化领域， 采用Matlab 语言编制了CGA、 SGA、迭代法和均匀布置的风振控制优化程序， 对比了各种算法的计算效率和各工况下的风致振动响应，得出以下结论：

（1）CGA 比SGA 的 计 算 效 率 最 高 提 高 了29%， 两种算法都能在规定的截止代数内收敛。 虽然均布和迭代工况的运算时间较短， 但其风致振动响应比CGA 和SGA 更大。

（2）CGA 工况的风致振动响应最小， 在总等效阻尼系数相等的情况下附加阻尼比与均布和迭代相比最大分别增大61%和22%， 顶层加速度最大分别减小15%和12%， CGA 对加速度响应的优化效果比对顶层位移和最大层间位移角的更好。

（3）混沌遗传算法可以合理地分布阻尼系数来减小结构的风致振动响应， 对于采用CGA 优化的结构来说， 等效阻尼系数宜主要布置于中下部楼层， 且自下向上逐层递减， 在刚度产生变化的楼层处突变。

[1] Q S Li， DK Liu， N Zhang. Multi-level design model and genetic algorithm for structural control system optimization[J]. Earthquake Engineering and Structural Dynamics，2001， 30（6）： 927-942.

[2] A S Ahlawat， A Ramaswamy. Multiobjective optimal fuzzy logic control system for response control of wind-excited tall buildings [J]. Journal of Engineering Mechanics，2004， 130（4）： 524-530.

[3] YQ Ni， ZG Ying， JY Wang. Stochastic optimal control of wind-excited tall buildings using semi-active MR-TLCDs[J]. Probabilistic Engineering Mechanics， 2004， 19（3）：269-277.

[4] JY Wang， YQ Ni， JM Ko. Magneto-rheological tuned liquid column dampers(MR-TLCD) for vibration mitigation of tall buildings: modeling and analysis of open -loop control[J]. Computers & Structures， 2005， 83 (25-26)：2023-2034.

[5] HS Kim， JW Kang. Semi-active fuzzy control of a windexcited tall building using multi -objective genetic algorithm[J]. Engineering Structures， 2012， 41： 242-257.

[6] J Suhardjo， BF Spencer Jr， A Kareem. Frequency Domain Optimal Control of Wind-Excited Buildings [J]. Journal of Engineering Mechanics， 1992， 118 (12）： 2463-2481.

[7] Osamu Furuya， H Hamazaki， S Fujita. Proper placement of energy absorbing devices for reduction of wind-induced vibration caused in high-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1988（74-76）：931-942.

[8] 汪大洋， 周云. 基于GA 优化理论的高层结构风振控制研究[J]. 土木工程学报， 2008， 41（1）： 42-47.

[9] 李红芳. 混沌遗传算法与结构优化设计[D]. 天津： 天津大学， 2004.

[10] 周云， 徐赵东， 邓雪松. 粘弹性阻尼结构中阻尼器的优化设置[J]. 世界地震工程， 1998， 14（3）： 15-20.

[11] 姚俊峰， 梅炽， 彭小奇. 混沌遗传算法（CGA）的应用研究及其优化效率评价[J].自动化学报， 2002， 28（6)）： 935-942.

[12] 王小平， 曹立明. 遗传算法一理论、 应用与软件实现[M]. 西安： 西安交通社。 2002.

[13] 孙瑞祥， 屈梁生. 遗传算法优化效率的定量评价[J].自动化学报， 2000， 26（4）： 552-556.

[14] 瞿伟廉， 程懋堃， 毛增达， 等. 设置粘弹性阻尼器钢结构高层建筑抗震抗风设计的实用方法[J]. 世界地震工程， 1998， 19（3）： 42-57.