水位观测资料的小波变换及异常提取
2014-08-06刘水莲全建军陈美梅吴劲柏
刘水莲, 全建军, 陈美梅, 吴劲柏
(1. 永安地震台, 福建 永安 366000; 2. 福建省地震局, 福州 350003)
0 引言
小波分析采用改变时间-频率窗口形状的方法, 很好地解决了时间分辨率和频率分辨率的矛盾, 它的主要特点是通过变换能够充分突出问题某些方面的特征, 因此小波分析对不同频率信息的识别功能较强。 该概念经由法国地球物理学家Morlet 与Grossmann 在分析处理地球物理勘探资料时提出后, 大量的数学家从各个方面的研究促进了它的发展, 直至1989年S.Mallat 提出了二进小波变换的快速算法, 从而使小波变换得到了广泛应用[1-3]。 小波变换理论在地球物理与勘探等方面得到广泛应用, 近年来国内同行越来越多将它应用到地震前兆资料的分析中[4-5]。 本文将应用小波分析对永安台水位资料进行处理, 提取与地震有关的前兆异常。
1 观测点概况
福建省地震局永安地震台建于1971年, 东经117.36°, 北纬25.89°, 位于政和-海丰断裂带西侧。 永安台模拟地下水观测井孔位于永安城区冷冻厂内, 井孔深度为1 000.44 m, 采用SW40-1 型水位计观测, 配套DYJ1 型盒式气压计和SJ1 型虹吸式雨量计辅助观测。 由于地处永安盆地, 常年雨水充沛, 支流丰富, 测点上游又有两个水库,一旦暴雨天气, 就有泄洪, 泄洪会引起水位的大幅度抬升。 因此, 永安冷冻厂井水位原始数据除了固体潮信息外, 还包含了许多天气干扰。
2 原理及方法
小波分析方法[4-6]是一种窗口大小(即窗口面积)固定但其形状可以改变, 时间窗和频率窗都可改变的时频局域化分析方法, 即在低频部分具有较高的频率分辨率和较低的时间分辨率, 在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被称为数学显微镜, 正式这种特性, 使小波变换具有对信号的自适应性。
小波变换的含义: 把一称为基本小波的函数ψ(t)做位移后, 再在不同尺度a 下与待分析信号x(t)做内积:

等效的频域表示是:

式(2)中, X(ω)、Ψ(ω)分别x(t)、 Ψ(t)是的傅立叶变换。
小波变换的时频窗口特性与短时傅立叶的时频窗口不一样, 因为仅仅影响窗口在相平面时间轴上的位置, 而不仅影响窗口在频率轴上的位置,也影响窗口的形状。 这样小波变换对不同频率在时域上的取样步长是可调节的, 即在低频时小波变换的时间分辨率正符合低频信号变化缓慢而高频信号变化迅速的特点, 这便是它比短时傅立叶变换具有更好的时频窗口特性。
2.2 小波基的选取
不同于傅里叶分析, 小波基不是唯一的, 一般情况下选择合适的小波基进行信号处理需考虑小波基的正则性和消失距、 所处理信号与小波基的相似性等几个因素, 在这点上正交小波变换有很大优势, 因为其所具有的离散特性和正交特性能够为我们的实际计算和实际应用带来方便。 函数按正交小波展开的分解算法和回复算法一起称为Mallat 算法[7], 这种算法为应用小波对信号分解重构提供了非常便捷的手段。 而对于正交小波,我们希望它同时具备有限支集、 光滑的、 超强的时域和频域的局部化能力等特性, 以便使Mallat算法更加快捷, 在信号分析处理中发挥突出的作用。 Daubechies 小波正是基于这样的要求构造出来的。 在张平等、 胡永钧等的分析结果中, 都证明了采用Daubechies 小波(db5)变换, 能够很好地对信号进行多分辨分析, 该小波正则性随阶数的增加而增加, 具有正交性, 有较好的信号自适应性[8-9]。本文也尝试使用Daubechies 小波进行信号处理,如图1 所示, 在选取dbN(N=1, 2, …10)小波函数进行分析后, 发现当N 取1~4 时, Daubechies小波不够光滑; 当N≥8 时, Daubechies 小波的消失 距 变 长, 衰 减 性 降 低; 而N 为5 ~7 时,Daubechies 小波形态与固体潮较相似。 因此, 本文将选取db6 小波进行数据处理。
3 处理实例
图2 是永安地震台2007年全年水位整点值的db6 小波6 层分离结果图, 由图可看到, 分离出的细节(高频,d1~d6)由第一层开始, 时间尺度按2的幂次逐层递增, 随分离层数的增加, 高频信息分离得越多,趋势曲线部分越来越清晰(a1~a6), 如同钟继茂在福建省数字化形变资料的异常分析中得到的结果[10], 本文中水位整点值分离后细节部分的第1 层是记录中的突跳、 台阶等高频信息; 第2、 3、 4 层出现的是明显的水位固体潮潮汐信息;第5 层包含的是水位缺数引起的干扰外, 还包含降水引起的滞后趋势抬升变化; 第6 层中突出信号已经能够与趋势部分(a6)的畸变变化基本同步,这部分有可能就是反映地震前后地下应力场变化的信息。

图1 db1 至db10 小波函数图Fig.1 Wavelet function diagram of db1 to db10
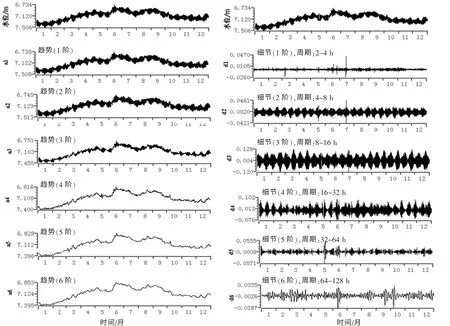
图2 永安地震台2007年全年水位整点值的db6 小波6 层分离结果图Fig.2 Wavelet decomposition figure 6 layer db6
4 震前异常提取
2007年, 福建地区发生了3 次4 级震, 分别是3月13日福建顺昌ML4.9 级、 6月12日华安ML4.0、 8月29日永春ML4.6 级地震, 震中距分别约为90 km、 110 km、 60 km。 图3 是对这三次地震前的db6 小波第6 层分解结果, 三次4 级震前, 水位存在不同程度的异常, 趋势异常形态为先下降, 而后在上升过程中或上升转平稳时发震,细节信息显示顺昌ML4.9 级地震震前异常从2007年2月8日开始, 持续33 天发震, 且震后效应持续至4月7日结束; 华安ML4.0 级地震震前异常从2007年5月28日开始, 持续15 天后发震, 震后效应持续至6月18日结束; 永春ML4.6 级地震异常从2007年7月29日开始, 持续31 天后发震, 无明显震后效应。
2008年福建地区发生了2 次4 级震, 分别是3月6日福建水口ML4.8 级、 7月5日长泰ML4.7级地震, 震中距分别约为120 km、 150 km。 图4是对这两次地震前的db6 小波第6 层分解结果,两次4 级震前, 水位趋势异常形态为波动变化,且幅度较小; 细节异常信息显示水口ML4.8 级地震震前异常从2008年2月20日开始, 持续14 天发震, 无明显震后效应; 长泰ML4.7 级地震震前没有明显的异常反应。

图3 2007年1~8月福建地区三次4 级地震异常对应图Fig.3 The corresponding figure of three M4 earthquakes anomalies in fujian area in 2007
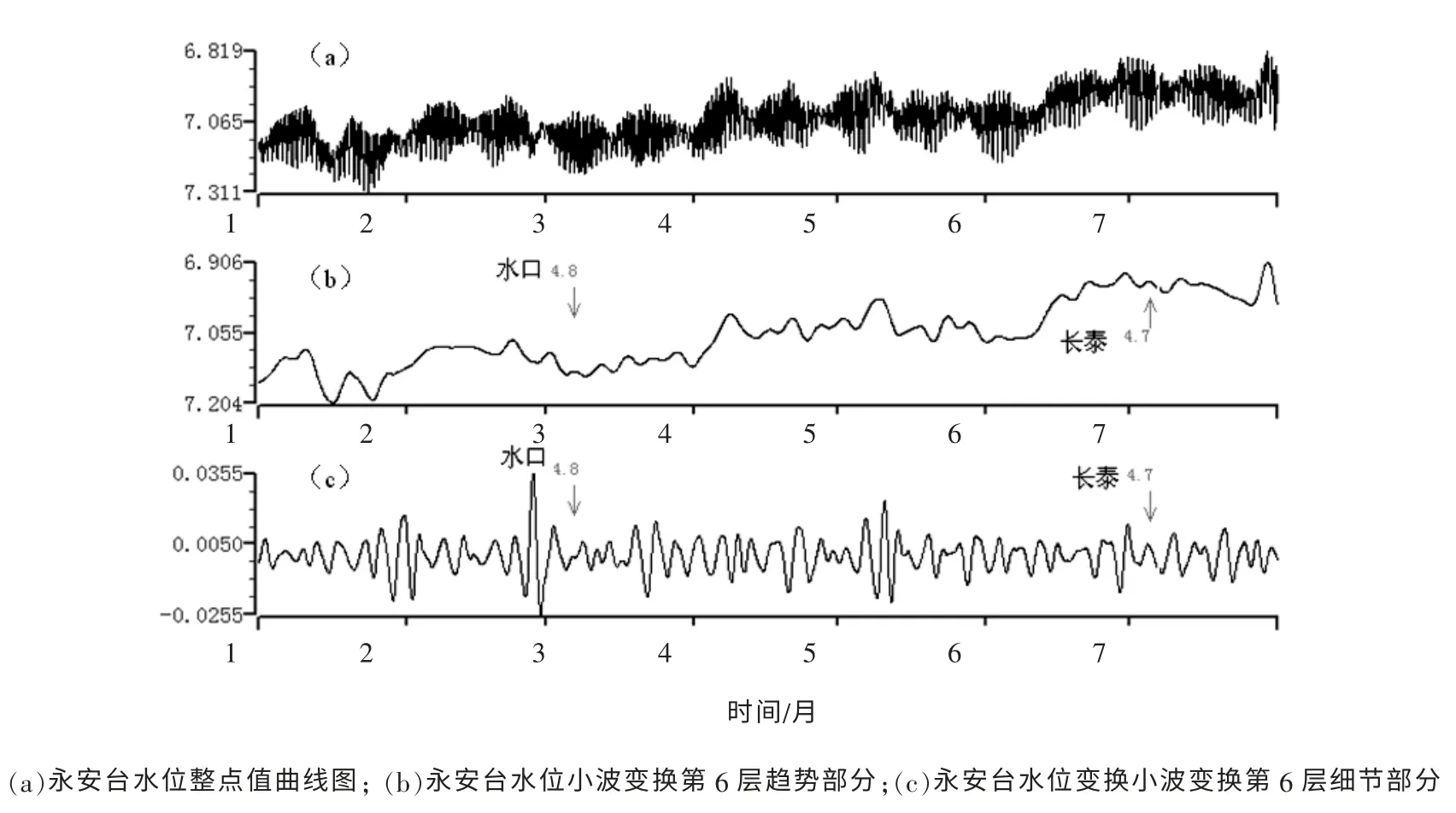
图4 2008年1~7月福建地区三次4 级地震异常对应图Fig.4 The corresponding figure of three M4 earthquakes anomalies in fujian area in 2008
从五次地震的分析结果来看, 福建中强震前,永安冷冻厂井水位异常平均在15~33 d 出现, 异常出现时间按长短排序为顺昌ML4.9 级→永春ML4.6 级→华安ML4.0→水口ML4.8 级, 这个结果不仅与震级大小有一定的关系, 与震中距也有明显的关系, 震级越大, 震中距越小, 异常出现的时间就越早, 我们就更加容易捕捉, 长泰ML4.7 级地震震前没有明显的异常反应, 与其震中距太大有关, 可以看出对于ML<5 级的地震, 永安冷冻厂井水位在150 km 范围内有一定的异常反应; 5 次地震中, 仅顺昌ML4.9 级、 华安ML4.0 级地震出现震后效应, 可见中强震发生时, 随着传播距离的加大, 能量释放衰减, 较少引起测点地下应力场的改变。
5 结论
(1)本文验证了小波变换这一新的信号处理方法使我们能够更直观地看清长年观测数据的变化趋势, 一些短临的变化也能更清晰地突显, 使各种长短期震前异常的识别变得更加容易, 更有利于利用前兆数据进行地震预测。
(2)对永安冷冻厂井水位整点值的小波分析结果显示, 频率分离的时间尺度按2 的幂次逐层递增, 随分离层数的增加, 高频信息分离得越多,趋势曲线部分越来越清晰, 细节部分第6 层中突出信号已经能够与趋势部分(a6)的畸变变化基本同步, 这部分有可能就是反映地震前后地下应力场变化的信息。
(3)通过分析, 发现对于ML<5 级的地震, 永安冷冻厂井水位在150 公里范围内有一定的异常反应; 在2007-2008年5 次中强震前, 永安冷冻厂井水位异常平均在15~33 d 出现, 异常出现时间不仅与震级大小有一定的关系, 与震中距也有明显的关系, 震级越大, 震中距越小, 异常出现的时间就越早, 而是否记录到震后效应, 却与前两者无明显关系, 这个结果对于地震三要素的预测有一定的意义。
(4)由于资料有限, 本文仅对2007—2008年福建地区的5 次中强震前的水位前兆异常进行了分析, 笔者将在下一步的工作中, 将继续利用小波方法, 对距离更远, 震级更大的地震进行分析,使得能够对永安冷冻厂井水位的映震能力有个更加准确的评估。
[1] Morlet J G, Arens G, Fourgeau E.Wave propagation and sampling theory: complex signal and scattering in mutilayered media[J]. Geophysics, 1982, 47(2): 203-211.
[2] Grossmann A, Morlet J.Decomposition of hardy function into square integrable Wavelets of contant shape [J].Silamj.Math.Anal., 1984, 15: 723-726
[3] Mallat S.Multiresolution Approximations and Wavelet Orthogonal Bases of L2(R)[J]. IEEE.Trans.AMS.,1989, 315: 68-87.
[4] 宋治平, 武安绪, 王梅, 等.小波变换在前兆观测资料分析中的应用[J]. 中国地震, 2004, 20(3): 31-38.
[5] 杨从杰, 冯志生, 等.小波分析方法在提取井水位潮汐因子震前变化特征的初步应用[J]. 西北地震学报,2005, 27(6): 163-167.
[6] 胡永钧, 屠泓为, 吴进. 小波分析在青藏高原东北缘地区地震前兆观测资料处理中的应用[J]. 高原地震,2008, 20(1): 14-21.
[7] 易志刚, 邱泽华, 等, 首都圈地区数字化钻孔应变观测资料分析[J].大地测量与地球动力学, 2006, 26(3):53-58.
[8] 张德丰. Matlab 小波分析工程与应用[M]. 北京:国防工业出版社, 2008.
[9] 胡永钧, 屠泓为, 吴进. 小波分析在青藏高原东北缘地区地震前兆观测资料处理中的应用[J]. 高原地震,2008, 20(1): 14-21.
[10] 钟继茂, 陈光. 福建省数字化形变资料的异常分析[J].华南地震, 2009, 29(3): 98-103.
