基于非线性时频分析的地震和爆破识别
2014-08-06朱新运钟羽云陈晓燕
张 帆, 朱新运, 熊 丹, 钟羽云, 陈晓燕
(1. 浙江省地震局, 杭州 310013; 2. 河北省地震局, 石家庄 050021)
0 引言
自开展地震观测以来, 如何区分地震及爆破就成为地震观测研究的基础课题, 并已经产生了大量的科技成果, 随着数字地震观测、 计算机技术、 数学算法等的发展, 在最新的观测及算法条件下, 通过相关指标定性、 定量的识别地震及爆破有广阔的研究空间。 在我国20 世纪70年代,可以从波形的图像对比法、 振幅与周期关系法[1]等方法来区分地震和爆破。 8O年代以来, 傅淑芳、张诚、 赵荣国等从波形、 波谱、 P 波初动、 振幅比及尾波衰减等方面对爆破识别进行了研究[2-4], 得出了大致相同的结果。 很多工作人员把这些方法应用到了工作中, 并利用波谱求出震源参数来区分地震和爆破[5-6]。 遗传BP 网络[7-8]、 分形分析[9]也被应用于地震和爆破的识别。 以前广泛应用的波谱分析方法, 把地震波作为是平稳信号, 利用傅立叶分析处理[10-11]。 随着数字信号处理的发展, 研究者发现地震波是一种极为复杂的随机波, 所产生的地震信号具有短时、 突变等特点, 是一种典型的非平稳随机信号[12], 因而反映地震波非平稳特征的线性时频分析方法被应用到地震分析及识别爆破中, 刘希强等提出小波变换能量线性度方法识别天然地震与爆破或塌方[13], 还利用高斯线调频连续小波变换的时频能量衰减因子方法来识别[14]。孙甲宁, 夏爱国, 苏乃秦用小波分析方法得到了乌鲁木齐台记录的天然地震和人工爆破在时频域的能量分布特征[15]。 笔者对比了波恩一约旦(Born-Jordan)、 乔伊一威廉斯(Choi-Williams)、 赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)、 维格纳(WV)四种非线性时频分析方法[16], 发现赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)时频分析方法, 抑制交叉干扰项的效果和时频聚集性更好, 更适合于分析地震波。 本文利用赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)时频分析方法分析浙江省的地震和爆破, 得到他们的时频谱特征。
1 理论和方法
时频分析方法, 主要是研究信号在时频域上的能量密度是如何变化的, 它不仅可以同时用时间和频率描述信号的能量密度, 而且能计算出任何密度。
所有的时频分布都可以由下面的方程得到:
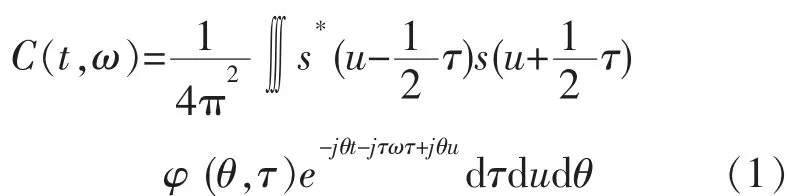
(1)式中φ (θ,τ)是二维函数叫做核[17], 式中*表示解析信号复共轭。 取不同的核函数可得到不同的时频分布。
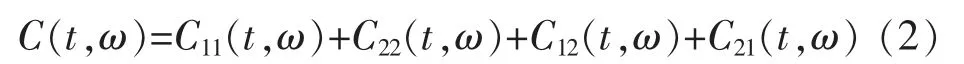
由于时频分布是信号的双线性函数,两个信号和的时频分布并不是每个信号的时频分布之和,而多了两个附加项叫做交叉干扰项,(2)式中C11(t,ω), C22(t, ω), C12(t, ω), C21(t, ω)分别是s1(t), s2(t)的自项和他们之间的交叉干扰项, 且C12(t, ω)=C21(t, ω)。

(3)式中ω12=(ω1+ω2)/2, 通过交换角标1 和2, 就可以得到C22和C21。 那么K(ω)的性质决定了交叉干扰项的大小和分布[18], 而核φ(0,τ)又唯一确定了K(ω)。 对于赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)时 频 分 布, 取 核在赵一阿特拉斯一马克斯的原著中, g(τ)取1, α 取1/2, 则
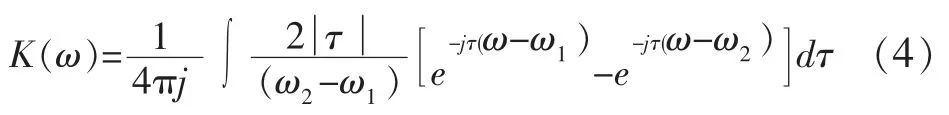
(4)式中可以看出K(ω)是ω-ω1和ω-ω2的函数,这些地方正好是自项的地方, 即交叉干扰项完全位于自项中间, 而其它时频分布的交叉干扰项均未完全位于自项中间。 将(4)式代入(3)式, 求得K(ω)后, 代入(2)式, 即可得到赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)时频分布。
此外, 对于任何的统计量x, 如果知道了它的分布P (x) 后, 可以求出该统计量的n 阶矩, 即xn的平均值, 也就是

矩具有很多方面的重要意义: 首先, 一阶矩给出了分布的基本性质的表示; 其次, 知道的矩阶数越高, 关于分布的了解就越多; 第三, 对于性能良好的分布, 矩唯一地确定了分布。 可以根据矩的理论求出信号和信号傅立叶变换的矩, 得到信号的时间局域特性和频率局域特性。 在时间域中,
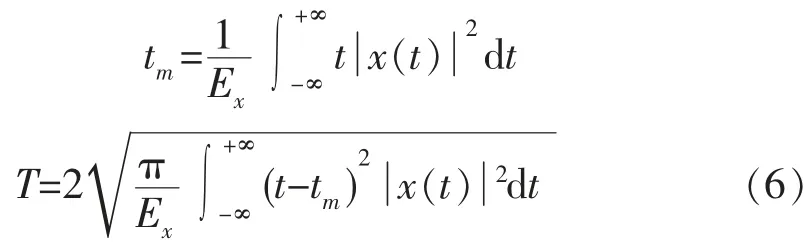
(6)式中tm为平均时间, T 为时间散布。
在频率域中,

(7)式中X(ν)为x(t)的傅立叶变换, 其中fm为平均频率, F 为频率散布。
2 资料选取
选取浙江省数字化地震台网的观测资料来分析。 为了减小地震波在传播过程中介质的影响,尽量选取震中距最小的台站记录的爆破和地震进行分析。 地震仪的频带不同所记录到的地震波的波形也有所不同, 选取的地震波都是短周期地震仪记录到的波形。 此外, 由于爆破的震级大部分都在ML3 级以下, 在挑选地震的时候, 也应该挑选震级在ML3 级以下的地震来进行对比分析。 根据以上的原则, 挑选了2000年3月至2006年5月间浙江省台网记录到的安吉爆破、 鄞县地震、文成地震、 嵊州地震、 桐庐地震共51个事件进行了分析和对比, 其中爆破11个, 地震40个, 震级范围在ML1.5 和ML3.1 之间。 所选事件的震中分布和浙江省的台站分布如图1 所示。
选择离震中最近的台站的地震记录来分析,台站的震中距大部分都在20 km 以内。 事件及所选台站仪器参数见表1。
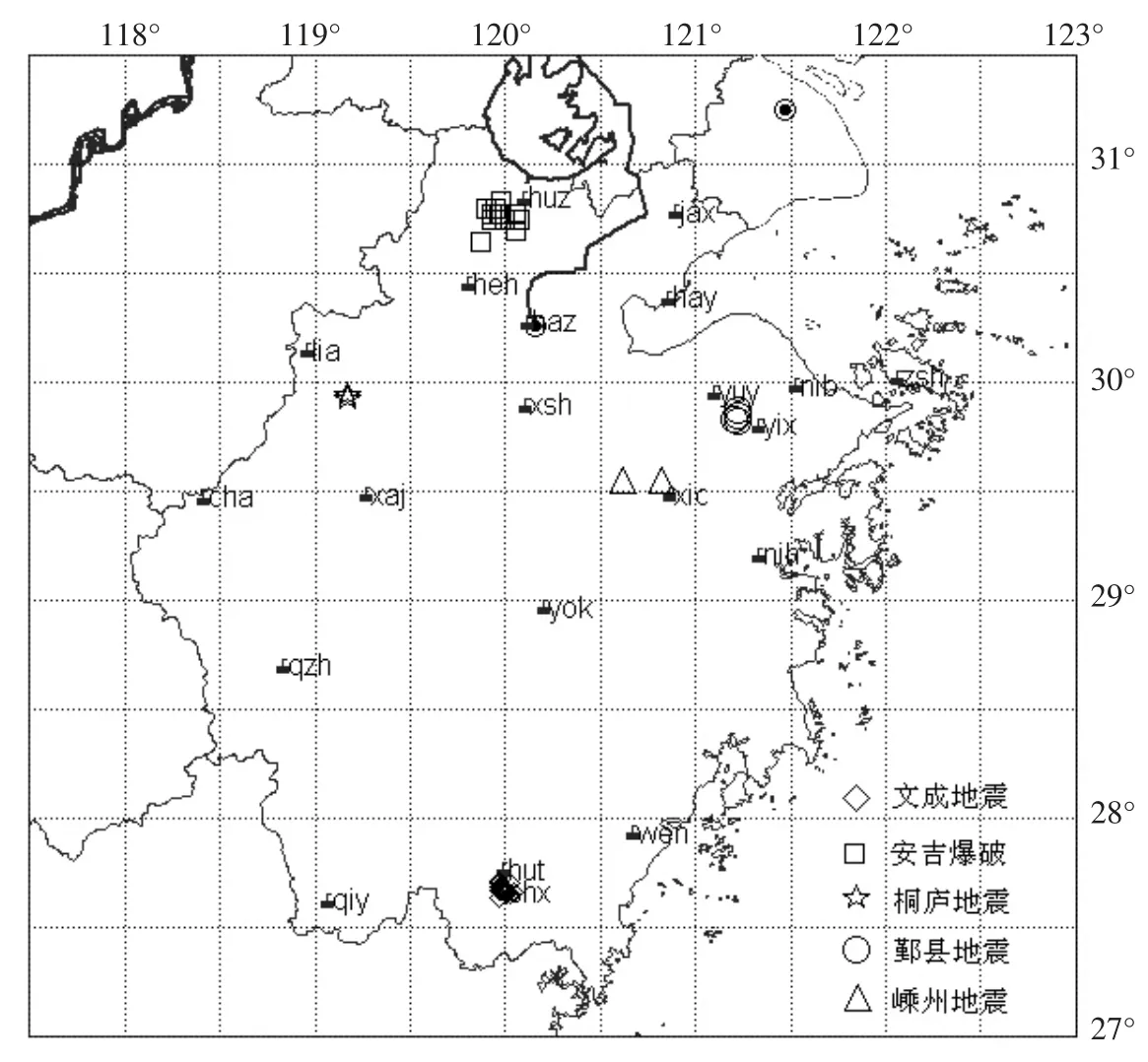
图1 震中分布和浙江省台站分布图Fig.1 Distribution map of epicenters and stations

表1 所选台站仪器参数表Table 1 The instrument parameter of selected stations
3 计算方法和结果
对每一个事件波形的三个分量分别经过如下处理得到时频分布: 第一步, 利用Matlab 中的detrend 函数去倾, 再读入仪器零极点文件得到传递函数, 用简单易行的傅里叶分析法即用地震记录的频谱除以传递函数扣除仪器响应后经过反傅立叶变换[19]恢复地动速度; 第二步, 根据仪器的频带范围有选择地进行带通滤波(本文中所选择的滤波范围为0.5~20 Hz)后, 按照累计梯形积分法,利用Matlab 中提供的cumtrapz 函数[20]对记录进行积分得到了位移记录; 第三步, 从位移记录中分别截取P 波和S 波进行Hilbert 变换得到它们的解析信号后, 求出赵-阿特拉斯-马克斯(Zhao-Atlas-Marks)时频分布, 以及P 波和S 波的平均频率fm、频率散布F, 平均时间tm、 时间散布T。 最终, 时频分布以等值线的形式给出。 典型的爆破和地震P波的时频谱如图2 和图3 所示。
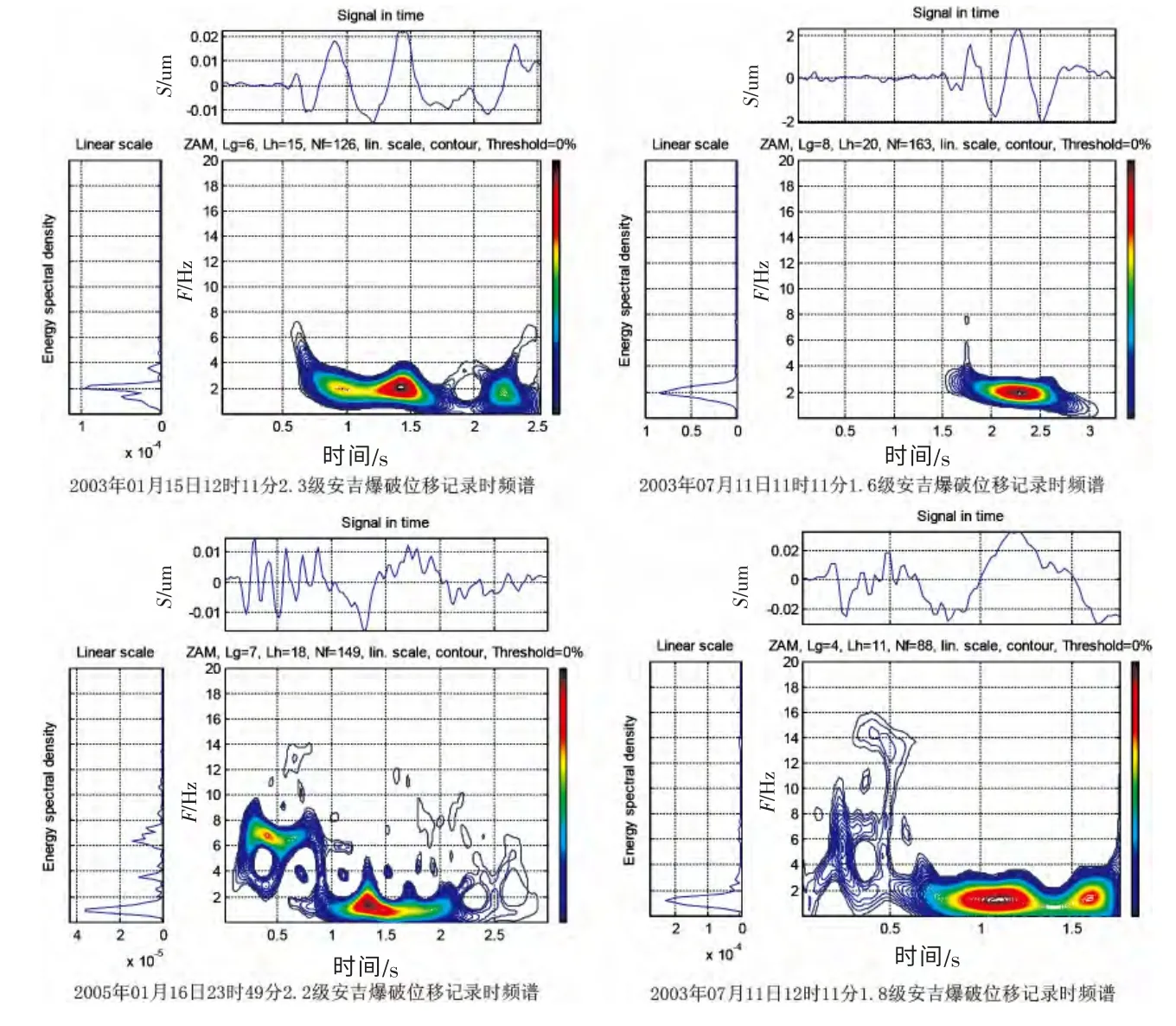
图2 爆破位移记录P 波时频谱图Fig.2 The P wave time-frequency spectrum of explosion displacement record
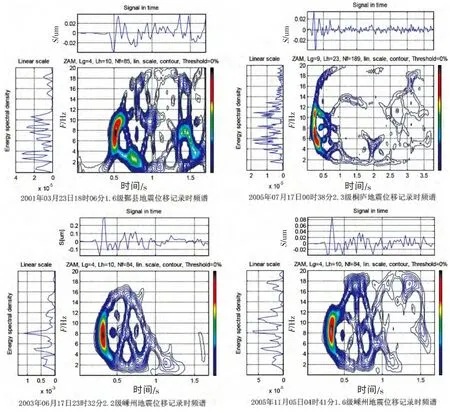
图3 地震位移记录P 波时频谱图Fig.3 The P wave time-frequency spectrum of earthquake displacement record
从图2 和图3 中可以看出, 相对于爆破P 波的时频谱图, 地震的时频谱要分散一些。 爆破的P波的时频谱峰值主要集中在1~8 Hz, 地震的P 波的时频谱峰值主要集中在6~12 Hz。 爆破和地震S波的时频谱图分别如图4 和5 所示。

图4 爆破位移记录S 波时频谱图Fig. 4 The S wave time-frequency spectrum of explosion displacement record

图5 地震位移记录S 波时频谱图Fig.5 The S wave time-frequency spectrum of earthquake displacement record
从图4 和图5 中同样可以看出, 相对于爆破S波的时频谱图, 地震的时频谱要分散。 爆破的S波的时频谱峰值主要集中在2 Hz 左右。 地震的S波时频谱峰值主要集中在2~12 Hz。 爆破的P 波时频谱峰值主要分布在2 Hz 左右的区域里, 而地震的时频谱峰值, 在频率高和低的区域都有分布。 爆破的S 波时频谱的最大峰值主要分布在较低的区域, 大约在1~2 Hz, 同样地震的S 波多数时频谱相对来说有很多个峰值, 并且峰值出现的地方不如爆破有规律性, 有的峰值出现在频率较高的区域, 有的峰值出现在频率较低的区域。
地震的时频谱相对与爆破来说比较 “分散”,而爆破的时频谱相对于地震来说比较 “集中”。 S波最大振幅为S 波到达1~2 s 后, 主要频率成分为2 Hz 左右, 这是由于S 波到达后, 短周期瑞利面波在此时出现。
爆破和地震的平均时间tm和平均频率fm有明显的不同。 对于P 波我们仅讨论平均频率。 爆破和地震的P 波平均频率如图6 所示。

图6 爆破和地震位移记录P 波的平均频率(a:UD;b:EW;c:NS)Fig.6 The average frequency of the P wave of explosions and earthquakes displacement record (a:UD,b: EW,c:NS)
从表2 中看出, 爆破P 波的平均频率比地震的平均频率低很多, 甚至不是一个数量级的, 爆破P 波平均频率fm为1.7~4 Hz, 地震S 波平均频率为6~12 Hz。
分析S 波时, 同时考虑S 波的平均时间和平均频率, 如图7 所示。

表2 爆破和地震P 波平均频率fm 对比表Table 2 The fm comparison table of P wave between explosions and earthquakes
从表3 看出, 爆破S 波三个分量的平均频率fm为1~2 Hz, 不同分量平均时间tm有所不同, 约在1~11 s 之间, 地震S 波三个分量的平均频率fm有所不同, 频率范围比较广, 约在3~11 Hz 之间,平均时间tm在0.4~2.5 s 之间, 甚至有小于1 s 的事件, 而爆破都是大于1 s 的。 无论哪个分量, 爆破的时频中心相对于地震分布在时间—频率面的右下角, 而地震的时频中心相对于爆破分布在时间—频率面的左上角, 这种说明了地震的频率比爆破的频率高, 地震的振幅比爆破的振幅先达到最大值。
4 结论与讨论

图7 爆破和地震位移记录S 波的平均频率和平均时间(a:UD;b:EW;c:NS)Fig.7 The average frequency and time of S wave of explosions and earthquakes displacement record (a:UD, b: EW, c: NS)

表3 爆破和地震S 波平均频率fm 和平均时间tm 对比表Tabel 3 The comparison table of fm and tm of S wave between explosions and earthquakes
选取了浙江省数字化地震台网提供的一些爆破和地震记录共51个事件(其中爆破11个, 地震40个), 经过预处理、 扣除仪器响应后, 分别求出位移记录的ZAM 时频分布后, 得到它们的时频谱的差异如下:
(1)地震P 波的平均频率大于爆破P 波的平均频率。
(2)地震S 波的平均频率大于爆破S 波的平均频率, 地震S 波的平均时间小于爆破S 波的平均时间, 表现为地震的平均时频中心相对于爆破分布在时间—频率面上左上角。
(3)无论是从P 波还是从S 波的时频谱看,地震的时频谱有多个峰值, 而爆破的时频谱仅有一个或者两个峰值。
(4)爆破的时频谱的时频聚集性比地震的时频聚集性好。
爆破和地震时频谱这些差异和它们俩之间的震源、 介质、 传播过程等的不同是密切相关的。理想情况下, 爆炸源只产生P 波和次生瑞利面波(国外称为Rg 波), 爆炸点附近岩石的不均匀性导致比浅源地震弱的S 波[21]。 这种Rg 波在震中距7~90 km 的范围内其最大振幅明显大于S 波最大振幅, 在爆破记录中以优势波出现[22], 而地震波形的各道记录中却没有发现这种波[23], Rg 波周期比S波周期大。 而在分析的地震和爆破中, 该震相在S波到达后的1~2 s 内到达, 导致爆破S 波时频谱的峰值出现在S 波到达后的1~2 s 内, 频率为1~2 Hz。 在时频面上表现为爆破的平均时频中心相对于地震来说处位于时间—频率平面右下角的区域。
地震震源较深, 频率成分复杂, 而爆破的震源浅, 经过松散地层, 高频成分被吸收的多, 因此, 地震的P 波的平均频率和S 波的平均频率都比爆破的要高。 爆破的震源是膨胀源, 相对于地震来说破裂和震源机制比较简单, 爆破所产生的波也相对于地震来说比较简单, 频率成分也比较单一, 时频谱相对地震来说聚集性较好。
时频分析方法将地震和爆破看作一种非平稳信号来处理, 可以很好地描述地震波的频率随时间的变化特征, 同时在时间尺度和频率尺度描述地震波的能量分布, 而傅立叶分析仅仅只能在频率域研究不同频率的能量大小。 因此该方法除了可以识别爆破和地震以外, 还可以对地震和爆破的复杂性经行研究。 但该方法的计算过程复杂,运算速度有待提高。
[1] 张少泉. 近震分析[M]. 北京: 地震出版社, 1977.
[2] 傅淑芳, 刘宝诚, 李文艺. 地震学教程(下册)[M]. 北京:地震出版社, 1980.
[3] 张诚. 地震分析基础[M]. 北京: 地震出版社, 1988.
[4] 时振粱, 强少泉, 赵荣国, 等. 地震工作手册[M]. 北京: 地震出版杜, 1990.
[5] 张萍, 蒋秀琴, 苗春兰, 等. 爆破、 矿震与地震的波谱差异[J]. 地震地磁观测与研究, 2005, 26(3): 24-34.
[6] 许健生, 尹志文. 地震与爆破的波谱差异[J]. 地震地磁观测与研究, 1999, 20(3): 18-23.
[7] 边银菊. 遗传BP 网络在地震和爆破识别中的应用[J]. 地震学报, 2002, 24(5): 516-524.
[8] Dowla F U ,Taylor S R ,Anderson R W. Seismic discrimination with artificial neural networks:Preliminary results with regional spectral data[J]. Bull Seism Soc A m ,1990, 80: 1346-1373.
[9] 刘代志, 邹红星, 韦荫康. 分形分析与核爆地震模式识别[J]. 模式识别与人工智能, 1997, 10 (2): 153-158.
[10] 林秀英, 张志呈. 爆破地震波的频谱分析[J]. 中国矿业, 2000, 9(6): 77-80.
[11] 郭学彬, 肖正学, 张志呈, 等. 爆破地震波的频谱特性研究[J]. 化工矿物与加工, 1999, 7: 18-20.
[12] Dowding C H.Monitoring and control of Explosioning effects [M]. Mining Engineering Handbook. Prentice Hal1.1985, 746-760.
[13] 刘希强, 沈萍, 张玲, 等. 用小波变换能量线性度方法识别天然地震与爆破或塌方[J]. 西北地震学报,2003, 25(3): 204-209.
[14] 刘希强, 沈 萍, 李 红, 等. 高斯线调频连续小波变换的时频能量衰减因子方法及其应用[J]. 中国地震,2003, 19(3): 225-235.
[15] 孙甲宁, 夏爱国, 苏乃秦. 地震和爆破时频域能量分布特征的对比分析[J]. 华南地震, 2005, 25(2): 68-74.
[16] 张 帆, 钟羽云. 时频分析方法及在地震波谱研究中的应用[J]. 地震地磁观测与研究, 2006, 27(4): 17-22.
[17] T.A.C.M.Claasen and W.F.G. mecklenbr?uker. The Wigner distribution-a tool for time-frequency signal analysis-PartⅢ :Relation with other time -frequency signal transformations [J]. Phlips Jour. Research,1998,35:372-389.
[18] L. Cohen. Time -Frequency Analysis: Theory and Application[M]. Englewood Cliffs:Prentice Hall, 1995.
[19] 陈运泰, 吴忠良, 王培德, 等. 数字地震学[M]. 北京:地震出版社, 2000.
[20] 李海涛, 邓樱. Matlab 6.1 基础及应用技巧[M]. 北京:国防工业出版社, 2002.
[21] 赵永, 刘卫虹, 高艳玲. 北京地区地震、 爆波和矿震的记录图识别[J]. 地震地观测与研究, 1995, 16(4):48-54.
[22] 山长仑, 张玲, 李永红, 等. 爆破短周期面波的分析[J]. 地震地磁观测与研究, 2001, 22(6): 43-48.
[23] 中国科学院地球物理研究所. 近震分析[M]. 北京: 地震出版杜, 1978.
