长期轴向荷载作用下钢骨混凝土柱的变形研究

陈周熠,吴建清,王 洋

(厦门大学建筑与土木工程学院,福建 厦门 361005)

钢骨混凝土柱结构是指在钢骨周围配置钢筋,并浇筑混凝土的柱结构,也称为型钢混凝土柱或劲性钢筋混凝土柱．由于钢骨混凝土柱结构具有强度高,刚性大,以及良好的延性及耗能性能,在地震区的高层及超高层建筑中的应用越来越广泛．很多学者已开展了关于钢骨混凝土柱结构的相关试验和理论研究[1-3],Shanmugam等[4]对此作了较深入的综述．这些研究主要集中在钢骨混凝土柱结构的极限承载力、黏结强度和抗震性能等方面,但对于长期荷载下由于混凝土的徐变和收缩引起的与时间相关的力学特性的研究还很少涉足．

徐变是在持续荷载作用下,混凝土结构的变形将随时间不断增加的现象．收缩则是混凝土在硬化过程中,由于各种原因引起的随时间变化而发生的体积缩小[5]．徐变和收缩会导致柱子在长期荷载作用下持续增长的变形．对钢骨混凝土柱中徐变和收缩特性的理解,以及对由它们所引起的长期变形的把握,将有助于在工程设计中对柱子的压缩变形进行精确分析,这一点对于高层建筑设计特别重要．

本文开展了钢骨混凝土短柱在长期轴向荷载作用下变形发展的试验研究,并基于试验结果,讨论了应用现有的徐变和收缩模型,采用龄期调整有效模量法来模拟钢骨混凝土柱在长期轴向荷载作用下的变形发展的适用性．

1 试验研究

1.1 试件设计及材料特性

由于长期加载试验要用到专门的徐变试验机,试件数量受到一定限制,本文共开展了3个钢骨混凝土短柱的长期荷载试验．试件断面形状参见图1,试件断面尺寸为160 mm×160 mm,高度为410 mm．试件S1-N1和S1-N2的钢骨采用80 mm×50 mm×4 mm (宽×高×腹板和翼缘厚度)的工字型钢,试件S2-N1采用80 mm×50 mm×7.8 mm的工字型钢．试件4角配置了直径12 mm的变形钢筋作为纵筋,采用直径8 mm的光圆钢筋作为箍筋,按间距100 mm布置．

图1 试件截面尺寸Fig.1 Cross section of test specimens

试件混凝土采用最大粒径为10 mm的砾石作为粗骨料,历时28 d，立方体抗压强度为fcu=39.1 MPa,弹性模量为Ec=21 000 MPa．柱中的工字型钢骨采用厚度分别为4和7.8 mm的钢板加工而成,4 mm厚钢板实测屈服强度为Fys=279 MPa,弹性模量为Es=204 000 MPa；7.8 mm厚钢板实测屈服强度为Fys=266 MPa,弹性模量为Es=205 500 MPa．所用直径12 mm变形钢筋的实测屈服强度为Fyr=436 MPa,弹性模量为Esr=201 000 MPa；所用直径8 mm光圆钢筋的实测屈服强度为Fyh=325 MPa,弹性模量为Esh=200 000 MPa．

1.2 长期荷载试验

为期202 d的长期荷载试验是在徐变试验机上进行的,在试件混凝土龄期达到28 d时开始加载．施加在试件S1-N1和S2-N1上的轴向长期荷载分别为345和375 kN,相当于试件在28 d龄期时的名义极限承载力的30%．选择这个应力水平,是因为高层建筑中的柱子在服役期的正常工作荷载下的轴压比通常在0.3左右．为了考察轴向长期荷载大小对于柱长期性能的影响,试件S1-N2采用460 kN的荷载值,相当于试件在28 d龄期时的名义极限承载力的40%．

试件加载期间的轴向应变值,是通过监测浇筑在试件侧面上的标距为150 mm的2个金属预埋件之间的长度变化来获得的．长度的测量和读取采用千分表进行,将千分表固定在其中一个预埋件上,千分表的滑杆则顶在固定于另一个预埋件的标杆上,每个试件都在其中2个对应侧面上安装了这套测量装置．试验环境的温湿度是通过温湿度自动测试仪进行监测采集．由于试验是在室内进行,监测数据表明,在试验加载期间的温湿度变化不大,因此可以不考虑温湿度变化的影响．

1.3 试验结果

各试件长期荷载试验得到的应变变化曲线参见图2．图中表示的应变值是荷载施加时的初始弹性应变和后期随时间增长的应变总和．如图2所示,试件S2-N1,S1-N1 和 S1-N2在加载202 d时最终的应变值分别达到了初始弹性应变值的1.93，2.22和2.73倍,试验表明在长期荷载作用下柱试件的变形增长较为显著．

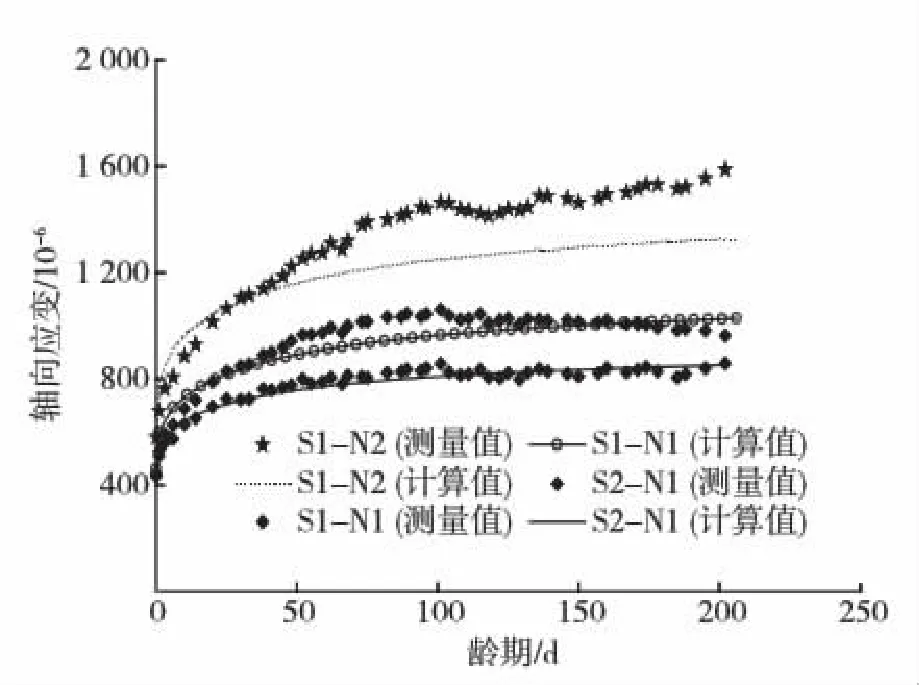
图2 长期荷载试验变形曲线Fig.2 Long-term strains during sustained load tests

如表1所示,试验参数包含了名义轴压比(长期荷载值与加载时名义极限承载力的比值)和钢骨含钢率(钢骨断面面积与柱截面面积的比值)．试件S1-N1和S2-N1轴压比相同,钢骨含钢率不同,试验结果表明,随钢骨含钢率的增加,长期变形值有所降低．试件S1-N1 和S1-N2则有相同的钢骨含钢率和不同的名义轴压比,结果表明,随轴压比的增加,长期变形值相应增大．由于徐变受混凝土应力水平的影响很大,所以这一点很容易理解．

表1 荷载试验参数Tab.1 Experimental variables of load test specimens

2 长期变形的计算

混凝土结构的长期变形计算主要包括两个方面的内容:1) 关于混凝土的收缩和徐变模型的选择;2) 采用什么分析方法在混凝土结构中考虑收缩和徐变的影响．

2.1 徐变和收缩预测模型

关于混凝土的徐变和收缩的预测,已有多种模型提出．其中ACI 209(1992)模型和CEB-FIP90模型是最常用的2种预测模型[6-7]．对这2种模型的预测效果,Gardner等[8]利用RILEM数据库进行了评估,该数据库汇集了来自世界各地的徐变与收缩的试验数据．他们的研究表明,ACI 209模型对于徐变的预测不太理想,与试验数据相比,低估了徐变值;而CEB-FIP90模型则对于收缩的预测不理想,因为其显著低估了收缩值．基于这个研究结果,本文对于徐变的预测选用了CEB-FIP90模型,而对于收缩的预测则选用了ACI209模型．

在选用ACI 209(1992)模型对本文试验中所用的混凝土收缩值进行预测时,所用的参数如下:相对湿度为60%,体表面积比(V/S)为160 mm,塌落度为50 mm,细骨料与整体骨料用量比值为34%,水泥质量浓度为512 kg/m3,含气量2%,早期潮湿养护1 d．

在选用CEB-FIP90模型对本文试验中所用的混凝土徐变值进行预测时,所用的参数如下:断面面积为25 600 mm2,断面与大气接触的周长为640 mm,相对湿度为60%,龄期28 d的混凝土平均抗压强度为32.5 MPa(这里采用的是150 mm×300 mm圆柱体抗压强度,是由实测的150 mm立方体抗压强度乘以一个转换系数0.83得到[9]),加荷龄期为28 d．

2.2 柱的长期变形分析方法

龄期调整有效模量法是在混凝土结构中计算由于徐变和收缩导致的应力和变形时最常用的数值分析方法之一[10]．根据龄期调整有效模量法,在时刻t时,混凝土总的应变值可以表示为在加载时刻τ0施加的初始应力σ0所产生的瞬时应变和徐变,由t时刻的应力增量Δσ(t)产生的瞬时应变、徐变和收缩应变的和,即:

(1)

式中:Ec(τ0)是τ0时刻混凝土的弹性模量,φ(t,τ0)是徐变系数,εsh(t)是收缩应变,χ(t,τ0)为老化系数,用于计算当应力是逐渐增加时的徐变．

式(1)中,徐变系数φ(t,τ0)和收缩应变εsh(t)可以从2.1节中介绍的预测模型得到,老化系数χ(t,τ0)选用文献[11]给出的经验表达式:

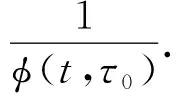
(2)

对于本次长期荷载试验的钢骨混凝土短柱,柱子承受恒定的轴向压力．假定钢材为线弹性,利用式(1)所描述的混凝土本构方程,再结合柱子在任何时刻应该满足的内外力平衡方程以及截面的变形协调方程,可以求得由于混凝土的收缩和徐变导致的柱随时间发展的变形．具体的分析过程和步骤可以参见文献[12]．

2.3 分析结果与试验曲线的比较

按上述方法求得柱子随时间发展的变形曲线,与实测曲线进行比较,如图2所示．对试件S2-N1和 S1-N1,分析结果与实测结果吻合良好．但对试件S1-N2,分析结果低估了实测的长期变形值．其原因可能在于,试件S1-N2的长期荷载轴压比较高,柱中的混凝土发生了非线性徐变,而这部分非线性徐变的效应,在分析时没有考虑．

3 结 论

本文开展了钢骨混凝土短柱在长期轴向荷载作用下变形发展的试验研究,并采用龄期调整有效模量法进行了分析计算,得到以下结论:

在长期荷载作用下柱试件的变形增长较为显著．试件S2-N1,S1-N1 和 S1-N2在加载202 d时最终的应变值分别达到了初始弹性应变值的1.93,2.22和2.73倍．长期变形值随钢骨含钢率的增加有所降低,但随轴压比的增加而相应增大．

采用ACI 209的收缩模型和CEB-FIP90的徐变模型,利用龄期调整有效模量法可以较好地模拟钢骨混凝土柱在长期轴向荷载作用下的变形发展．但对于长期荷载轴压比较高的柱,该方法会低估其长期变形值．

[1] El-Tawil S，Deierlein G G.Strength and ductility of concrete encased composite columns[J].Journal of Structural Engineering，1999，125(9)：1009-1019.

[2] Young B，Ellobody E.Performance of axially restrained concrete encased steel composite columns at elevated temperatures[J].Engineering Structures，2011，33：245-254.

[3] Denavit M D，Hajjar J F，Leon R T.Stability analysis and design of steel-concrete composite columns[C]∥Proceedings of the Annual Stability Conference.Grapevine,United States：Structural Stability Research Council，2012：98-116.

[4] Shanmugam N E,Lakshmi B.State of the art report on steel-concrete composite columns[J].Journal of Constructional Steel Research，2001，57(10)：1041-1080.

[5] Gilbert R I.Time effects in concrete structures[J].Developments in Civil Engineering，1988，23:361-365.

[6] Rhodes J A，Carreira D J.Prediction of creep,shrinkage,and temperature effects in concrete structures[M].Hills,United States:American Concrete Institute，1982.

[7] Comite Euro-International du Beton.CEB-FIP model code 1990:design code[M].London：Thomas Telford，1993.

[8] Gardner N J，Lockman M J.Design provisions for drying shrinkage and creep and normal-strength concrete[J].ACI Mater.Journal，2001，98(2)：159-167.

[9] 沈蒲生.混凝土结构设计原理[M].北京：高等教育出版社，2005：17-18.

[10] Bazant Z P.Prediction of concrete creep effects using age adjusted effective modulus method[J].ACI Journal，1972，69(4)：212-217.

[11] 孙宝俊.混凝土徐变理论的有效模量法[J].土木工程学报，1993，15(3)：66-88.

[12] Chen Z Y，Wang Y，Chen W.Deformation and stress redistribution of SRC columns under long-term axial compression[C]∥Proceedings of the 2011 International Symposium on Innovation & Sustainability of Structures in Civil Engineering.Xiamen，China:[s.n.]，2011:300-307.