非自治与随机动力系统的吸引子*

周盛凡

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

动力系统理论具有悠久的历史,但实质性的理论研究源于Poincaré与Birkhoff关于天体力学的工作[1].从当前的文献动态来看,动力系统的研究正从低维向高维和无穷维发展,从自治系统向非自治和随机系统扩展[2-5]. 无穷维动力系统的经典背景是流体力学中的湍流问题,其理论体系从20世纪80年代开始真正兴起,主要研究具有耗散性的系统当时间趋于无穷大时的渐近行为.至今描述自治动力系统的渐近行为的整体吸引子的理论体系相对已比较成熟[3,6-10].本文主要介绍无穷维非自治与随机系统吸引子方面的一些最新成果[2,4,8-15].

1 非自治动力系统的吸引子

实际问题中许多系统的内部参数和外部的受迫力或多或少地依赖于时间,包括周期、拟周期、概周期地依赖于时间,从而对非自治系统的研究就显得很有必要了[4].考虑非自治发展方程的初值问题

(1)

式(1)中:状态变量u的相空间E为Banach空间或Hilbert空间;F(t,u)明显依赖于时间t.假设问题(1)是适定的,则其解映射生成E上的一个双参数连续算子过程{U(t,τ)}t≥τ:U(t,τ):E→E,uτ→u(t),t≥τ,满足:1)U(τ,τ)=I,∀τ∈R;2)U(t,r)U(r,τ)=U(t,τ),-∞<τ≤r≤t<∞;3)(t,τ,uτ)|→U(t,τ )uτ(-∞<τ≤t<∞)是连续的.其中,U(t,τ)把τ时刻的初值uτ映到t时刻的解u(t).对于这样的非自治系统(1),解曲线(积分曲线或轨道)关于t轴上的平移不再是不变的,这与自治系统有着本质的区别,从而其解同时依赖于初始时刻τ与终值时刻t,不同于自治系统的解只依赖于终值时刻t与初始时刻τ之差t-τ.所以,描述自治系统的相空间上的整体吸引子不再适合描述非自治系统的解的渐近行为.此时必须在包含时间轴在内的扩展相空间上考虑解的演化性态,需要引入新的概念.主要有2个概念:一致吸引子与拉回吸引子.它们都是整体吸引子在非自治系统的推广.

1.1 一致吸引子

非自治系统(1)可以写成如下形式:

(2)

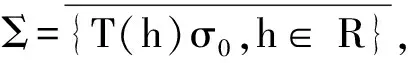
考虑一簇发展方程的初值问题

(3)

假设对于任意的σ∈Σ,问题(3)是适定的,则可得到连续算子过程簇{Uσ(t,τ)}t≥τ,σ∈Σ,其中τ∈R.

注1根据定义1,一致吸引子不要求是不变的,这里用“最小性”代替通常吸引子定义中的“不变性”.若一致吸引子存在,则必唯一.在具体应用中,通常要求符号空间Σ具有某种紧性,比如平移紧,即Σ在Θ中紧.Cb(R,M)中平移紧符号包括关于t是拟周期的函数与概周期函数等.具有平移紧符号的非自治系统的一个有趣特征是:可以把一致吸引子的构造转化为作用于适当扩展相空间上的半群(斜积流)的整体吸引子的存在性,并由此得到一致吸引子的一些重要性质.由于系统(3)的解的适定性,因而有平移恒等式

UT(h)σ(t,τ)=Uσ(t+h,τ+h),∀t≥τ,τ∈R,∀σ∈Σ,∀h∈R.

(4)

引入算子簇:S(t):E×Σ→E×Σ,(u,σ)→(Uσ(t,0)u,t(t)σ),∀t≥0,则{S(t)}t≥0为E×Σ上的半群,称为E×Σ上的斜积流.可以在E×Σ上考虑{S(t)}t≥0的整体吸引子的存在性,有下面的定理:

定理1假设过程簇{Uσ(t,τ)}t≥τ,σ∈Σ是(E×Σ,E)连续的且有紧的一致吸引集,则{S(t)}t≥0有连通的整体吸引子A.且如果Π1(Π2)表示E×Σ到E(Σ)上的投影算子,则AΣ=Π1A⊂E是{Uσ(t,τ)}t≥τ,σ∈Σ的一致吸引子,Σ=Π2A.

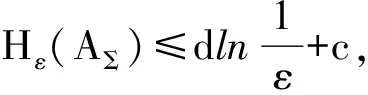
1.2 一致指数吸引子

下面介绍拟周期符号驱动下的非自治动力系统的解过程簇的一致指数吸引子的存在性及其构造,详见文献[12].

设Tn为n维环面:Tn={σ=(σ1,σ2,…,σn):σj∈[-π,π],∀j=1,2,…,n},其中

(σ1,σ2,…,σj,-π,σj+1,…,σn)～(σ1,σ2,…,σj,π,σj+1,…,σn),∀j=1,2,…,n.

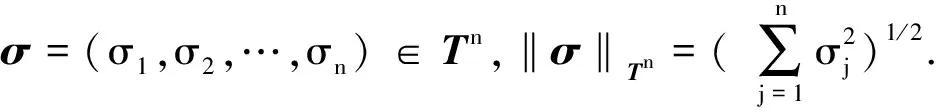
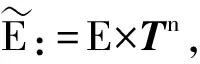
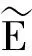
现在介绍一致指数吸引子的有关定义.设B表示E的闭有界子集,使得Uσ(t,τ)B⊆B,∀σ∈Tn,t≥τ,τ∈R.记BS=B×Tn,则{S(t)}t≥0为作用在BS上的连续半群,且∀t≥0,S(t)BS⊆BS.

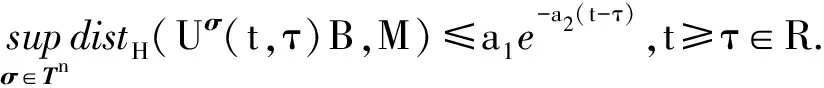
关于半群{S(t)}t≥0在BS上的指数吸引子和过程簇{Uσ(t,τ)}t≥τ,σ∈Tn在B上的一致指数吸引子的存在性,有下面的定理:

定理2若存在t*>0,L=L(t*)>0和E的N维子空间EN(N=N(t*)∈N),使得对于任意u1,u2∈B,σ1,σ2∈Tn,有

∀t∈[0,t*],

则

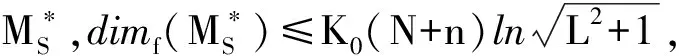
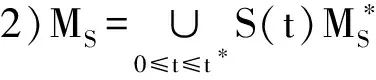
3)M=ΠB(MS)为过程簇{Uσ(t,τ)}t≥τ,σ∈Tn在B上的一致指数吸引子,其中ΠB表示有界投影BS→B.

1.3 拉回吸引子

考虑作用在Banach空间E上的连续算子过程{U(t,τ)}t≥τ.本节固定终止时间t,考虑初始时间τ趋于-∞时系统的向后的渐近行为,这时可用拉回吸引子来描述.拉回吸引子自Haraux在文献[11]中提出以来,得到了很大的发展.

定义3称集簇{A(t)}t∈R为过程{U(t,τ)}t≥τ的一个拉回吸引子,如果

1)∀t∈R,A(t)在E中紧;

2)A(t)在如下意义下是不变的:U(t,τ)A(τ)= A(t),∀t≥τ,τ∈R;

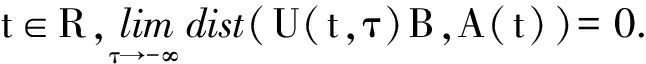
拉回吸引性3)是指:从-∞出发的初始有界集在时刻t处被A(t)吸引到其闭包内.由定义3可见,拉回吸引子如存在,不一定是唯一的.不过在附加一些条件后,可使拉回吸引子是唯一的,比如附加如下的“向后有界性'”:

(5)

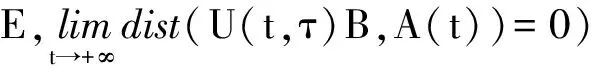
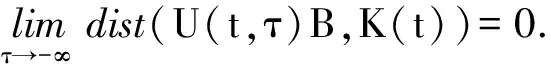
定理3假设过程{U(t,τ)}t≥τ有紧的拉回吸引集{K(t)}t∈R(∀t∈R,K(t)是紧的),则{U(t,τ)}t≥τ有拉回吸引子{A(t)}t∈R.若{K(t)}t∈R满足向后有界性(5),则{A(t)}t∈R是唯一的且满足该向后有界性(5).

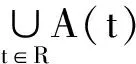
定理4设{U(t,τ)}t≥τ为可分Hilbert空间E上的连续过程,{A(t)}t∈R为E的一簇紧的负不变子集(即∀t≥τ,τ∈R,A(t)⊂U(t,τ)A(τ)).假设

1)∀t∈R,存在A(t)的直径为2的闭子集的一致有限覆盖,即∀t∈R,存在A(t)的直径为2 的N0个闭球的一致有限覆盖,其中N0与t无关;

2)对于任意τ∈R,存在与τ∈R无关的常数T≥0,L>0,0<η<1,γ>0及X的有限维正交投影P1,P2,使得对于vi∈A(τ),i=1,2,有

‖U(T+τ,τ)v1-U(T+τ,τ)v2‖E≤L‖v1-v2‖E,

‖U(T+τ,τ)v1-U(T+τ,τ)v2‖E≤

则对于每个s∈R,A(s)有有限的分形维数满足

1.4 拉回指数吸引子

由于拉回吸引子吸引有界集或轨道的速度有时很慢,这给实际应用与数值模拟带来很大不便,所以引进拉回指数吸引子就有必要了.接下来介绍一种非自治系统的拉回指数吸引子的构造方法,详见文献[13,17].

设E为Banach空间,范数为‖5‖E,E1为E的子集且关于E的度量构成度量空间.考虑E上2个参数的连续过程{U(t,τ),E1,E}t≥τ.

定义5称E1的子集簇{M(t)}t∈R为连续过程{U(t,τ),E1,E}t≥τ在E中的拉回指数吸引子,如果

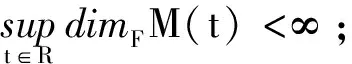
2)M(t)(t∈R)是正不变的,即U(t,τ )M(τ)⊂M(t),-∞<τ≤t<∞;

3)存在常数ε>0,使得对于任意有界集B⊂E1,存在TB>0与正值函数Q:R+×R+→R+,满足dist(U(t,τ)B,M(t))≤Q(‖B‖X,TB)e-ε(t-τ),τ∈R,τ+TB≤t<∞.

作如下假设:

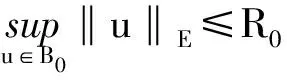
‖U(τ*+τ,τ)uτ-U(τ*+τ,τ)vτ‖E≤γ‖uτ-vτ‖E+‖Q(τ)uτ-Q(τ)vτ‖E,

‖Q(τ)uτ-Q(τ)vτ‖Z≤L2‖uτ-vτ‖E.

‖(I-PN)(U(τ+τ*,τ)uτ-U(τ+τ*,τ)vτ)‖E≤γ‖uτ-vτ‖E.

其中,γ,N∈N依赖于τ*但与τ无关.

定理5设{U(t,τ),E1,E}t≥τ为E上的连续过程.

1)若假设1)～3)成立,则{U(t,τ),E1,E}t≥τ存在拉回指数吸引子{M(t)}t∈R具有以下性质:

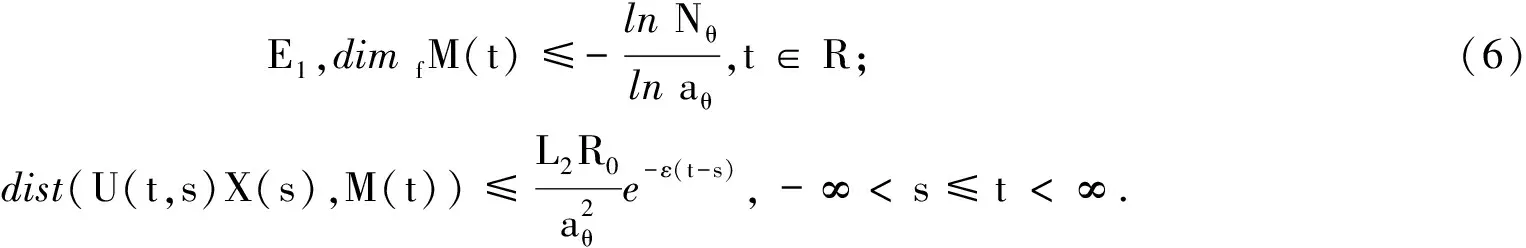
(7)

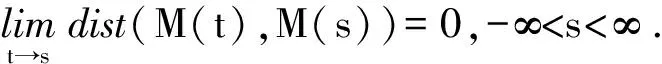
2 多值非自治和随机动力系统的吸引子

毫无疑问,非自治和随机动力系统在自然科学的许多应用领域中起着非常重要的作用.在许多实际问题中,通常遇到微分方程初值问题的解存在但不唯一或无法证明其唯一性的情况.例如,三维Navier-Stokes方程和具超临界增长非线性项的波动方程等.在这种情况下,已有的关于单值动力系统的理论中就有许多地方不成立了.下面介绍一下近年来国际上受到关注的多值非自治和随机动力系统的吸引子理论的部分结果.

2.1 拉回轨道吸引子

对于解存在但不唯一或唯一性尚未证明的情况下,不能利用经典方法研究相应半群或过程的吸引子,这时需要引入新的思想与工具.目前,在动力系统的解的唯一性缺乏的情形下,大致有3种方法处理由此引起的研究其渐近行为的困难.第1种方法是由Ball[18]提出的广义半流法;第2种是多值动力系统法[19-20];第3种方法是轨道吸引子[4].轨道吸引子的定义最初是为了克服由于3DNavier-Stokes方程的弱解可能不唯一所导致的困难而提出来的.后来,轨道吸引子理论被证明对于其他的模型在其初值问题的解可能不唯一时也是非常有用的.

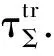
考虑非自治发展方程簇(3).对于t∈R+,设算子Fσ(t)(5):X|→Y是已知的,其中X,Y为Banach空间,使得X⊆Y,函数参数σ(t)属于某个Banach空间Σ,称为时间符号空间，并且存在Σ上的算子群θ={θt}t∈R满足θtΣ=Σ,∀t∈R.

假设对于每个σ∈Σ,方程(3)至少有一个解u(t)∈C(R+; Y)∩L∞(R+;X).由Lions-Magenes定理知,∀t∈R+,u(t)∈X.

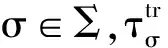
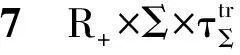
现在用Π+表示在区间R+=[0,+∞)上的限制算子(相对于时间变量);ΠT表示在区间[0,T]上的限制算子.例如,若u(5)∈C(R+;Y)∩L∞(R+;X),则ΠTu(5)∈C([0,T];Y)∩L∞(0,T;X):当t∈[0,T]时,有ΠTu(t)=u(t).

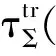
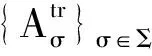
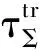
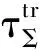
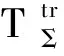
其中:P={Pσ}σ∈Σ为拉回轨道吸收集;“一杠”表示在Cloc(R+;Y)中取闭包;ωσ(P)表示P的拉回ω-极限集.

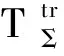
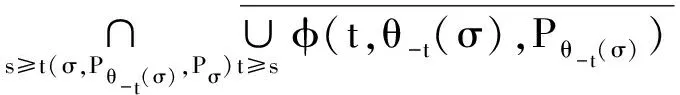
2.2 多值非自治和随机动力系统的拉回与随机吸引子

虽然已有了过程或多值系统余环吸引子的存在性理论,但很有必要建立多值系统的吸引子的更一般理论.这里介绍这方面的一些最新研究成果[15],它们是已有的关于非自治与随机动力系统结果的推广和发展,其理论体系还远未完善.

设Ω是一集合(相当于上面的符号空间),θ=(θt)t∈R是Ω上的群或流,即θ:R×Ω→Ω满足:θ0=I,θt+τ=θt∘ θτ:=θtθτ,∀t,τ∈R,则称Ω为非自治扰动流或非自治驱动系统.

设P:=(Ω,F,P)为概率空间.考虑P上的一个可测非自治流

θ:(R×Ω,B(R)⊗F )→(Ω, F ).

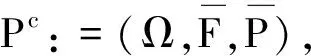
设E=(E,dE)为Polish空间(可分完备度量空间).记C(E)为所有具有非空闭像集的多值函数D:ω(∈Ω)→D(ω )(∈2E)组成的集合;记Pf(E)为E的所有非空闭子集组成的集合,于是,

D∈C(E)⟸⟹D:Ω→Pf(E).

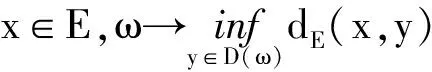
定义10称多值映射U:R+×Ω×E→Pf(E)为多值非自治动力系统(MNDS),如果

1)U(0,ω,5)=I;

2)U(t+τ,ω,x)⊂U(t,θτω,U(τ,ω,x)),∀t,τ∈R+,x∈E,ω∈Ω .

称多值映射U为严格MNDS,如果

3)U(t+τ,ω,x)=U(t,θτω,U(τ,ω,x)),∀t,τ∈R+,x∈E,ω∈Ω .

称一个MNDSU为多值随机动力系统(MRDS),如果多值映射(t,ω,x)→U(t,ω,x)是 B(R+)⊗F ⊗B(E)可测的,即对于每个开子集O⊂E,有{(t,ω,x):U(t,ω,x)∩O≢Ø}∈B(R+)⊗F ⊗B(E).

定义11称多值映射U(t,ω,5)为在x0∈E是上半连续的,如果对于集合U(t,ω,x0)的每个邻域U,存在 δ>0,使得当dX(x0,y)<δ时,U(t,ω, y)∈U.称U(t,ω,5)为在E上是上半连续的,如果它在每个点x0∈E处都是上半连续的.

引理1设Ω为Polish空间,F为其Borelσ-代数.若(t,ω,x)→U(t,ω ,x)是上半连续的,则该映射是可测的.

下面介绍MNDS的拉回与随机吸引子的有关定义及其存在唯一性定理.

定义12称多值映射D:ω→D(ω)为关于MNDSU 是负(严格或正)不变的,如果

D(θtω)⊂(=,⊃)U(t,ω,D(ω)),∀ω∈Ω,t∈R+.

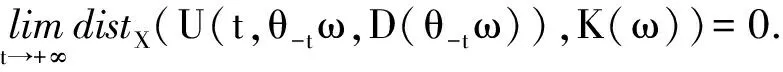
称D满足内闭性:若D∈D,D′∈C(E)满足:∀ω∈Ω,D′(ω)⊂D(ω),则D′∈D.

定义13称集A∈D为MNDSU的拉回D-吸引子,如果

1)∀ω∈Ω,A(ω)为紧集;

2)A为拉回D-吸引的;

3)A为负不变的.

注4若定义13条件3)中的“负不变的”换为“严格不变的”,则称A∈D为MNDSU的严格拉回D-吸引子.

定义14设U为MRDS,集A∈D具有定义13中的性质1)～3),且集合A关于概率空间P是随机集,则称A为MRDSU的随机拉回D-吸引子.

注5拉回收敛性与关于概率测度P的不变性直接导致吸引子的概率意义下的向前收敛性:∀t≥0,多值映射D:ω→U(t,ω,D(ω))可测,且

(概率1收敛).

这个性质仅是在概率弱收敛意义下成立,在几乎处处意义下一般不再成立.

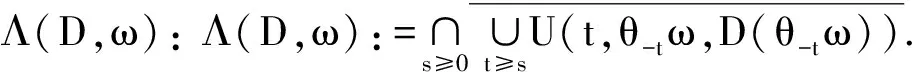
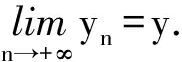
引理2假设对于t≥0,ω∈Ω,MNDSU(t,ω,5)是上半连续的.设B为多值映射使得U关于B是渐近紧的,即对于每个序列{tn}(tn→+∞),ω∈Ω,序列{yn∈U(tn,θ-tnω,D(θ-tnω))}是预紧的,则∀ω∈Ω,拉回ω-极限集Λ(D,ω)是非空的、紧的、且

⊂U(t,ω,Λ(D,ω)),∀t≥0.

定理7设引理2中的条件成立,且假设B∈D为拉回D-吸收的,则A(ω)=Λ(B,ω)为唯一的拉回D-吸引子;若U为严格的,则A为严格不变的.

定理8设U为MRDS且定理7中的条件成立,并设对于t≥0,ω→U(t,ω,B(ω))为随机集,又假设对于t≥0,ω∈Ω,集合U(t,ω,B(ω))为闭的,则A(ω)=Λ(B,ω)为可测的,从而A为随机拉回D-吸引子.

参考文献：

[1]Barrow-Green J.Poincaré and the three-body problem[M].Providence:Amer Math Soc,1999.

[2]Miranville A,Zelik S.Attractors for dissipative partial differential equations in bounded and unbounded domains[J].Handbook of Differential Equations:Evolutionary Equations,2008,4:103-200.

[3]Temam R.Infinite-dimensional dynamical systems in mechanics and physics[M].2nd ed.New York:Springer-Verlag,1997.

[4]Chepyzhov V V,Vishik M I.Attractors of equations of mathematical physics[M].Providence:Amer Math Soc,2002.

[5]Arnold L.Random dynamical systems[M].Berlin:Springer-Verlag,1998.

[6]Hale J K.Asymptotic behavior of dissipative systems[M].Providence:Amer Math Soc,1988.

[7]Robinson J C.Infinite-dimensional dynamical systems[M].Cambridge:Cambridge University Press,2001.

[8]Ladyzhenskaya O A.Attractors for semigroups and evolution equations[M].Cambridge:Cambridge University Press,1991.

[9]Sell G R,You Y.Dynamics of evolutionary equations[M].New York:Springer-Verlag,2002.

[10]Babin A V,Vishik M I.Attractors of evolution equations[M].New York:Access Online via Elsevier,1992.

[11]Haraux A.Attractors of asymptotically compact processes and applications to nonlinear partial differential equations[J].Comm Partial Differential Equations,1988,13(11):1383-1414.

[12]Zhou Shengfan,Han Xiaoying.Uniform exponential attractor for nonautonomous KGS and Zakharov lattice systems with quasiperiodic external forces [J].Nonl Anal:Theory,Methods & Applications,2013,78:141-155.

[13]Zhou Shengfan,Han Xiaoying.Pullback exponential attractors for non-autonomous lattice systems[J].J Dyna Diff Eqns,2012,24(3):601-631.

[14]Zhao Caidi,Zhou Shengfan.Pullback trajectory attractors for evolution equations and application to 3D incompressible non-Newtonian fluid[J].Nonlinearity,2008,21(8):1691-1717.

[15]Balibrea F,Caraballo T,Kloeden P,et al.Recent developments in dynamical systems:three perspectives[J].Inter J Bifurcation Chaos,2010,20(9):2591-2636.

[16]Zhou Shengfan,Zhao Caidi,Wang Yejuan.Finite dimensionality and upper semicontinuity of compact kernel sections of non-autonomous lattice systems[J].Dis Cont Dyna Systems,2008,21(4):1259-1277.

[17]Efendiev M,Yamamoto Y,Yagi A.Exponential attractors for non-autonomous dissipative system[J].J Math Soc Jpn,2011,63(2):647-673.

[18]Ball J M.Continuity properties and global attractors of generalized semiflows and the Navier-Stokes equations[J].J Nonlinear Sci,1997,7(5):475-502.

[19]Caraballo T,Langa J A,Melnik V S,et al.Pullback attractors of nonautonomous and stochastic multivalued dynamical systems[J].Set-Valued Analysis,2003,11(2):153-201.

[20]Wang Yejuan,Zhou Shengfan.Kernel sections and uniform attractors of multi-valued semiprocesses[J].J Differential Equations,2007,232(2):573-622.