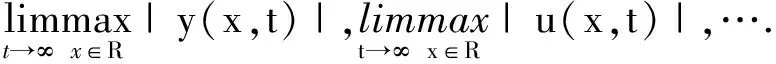Camassa-Holm方程的一些研究进展*

周 勇

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

1 基本性质与主要研究成果

本文主要讨论Camassa-Holm方程的Cauchy问题.Camassa-Holm方程可以写为

(1)

式(1)中:u(x,t)∈R表示波的高度;下标x和t表示对空间和时间变量做偏导数.早在1981年，Fuchsteiner等[1]在研究近似KdV方程时就推导出方程(1).但真正的物理推导是由Camassa等[2]在1993年刻画浅水区域的水波运动时完成的，所以一开始也称方程(1)为浅水波方程(shallowwaterequation).

关于方程(1)的基本性质，Camassa等在文献[2]中有比较全面的讨论,本文再提下面几点：

1)方程(1)是一个完全可积系统，有无穷多个守恒律.例如，如果下面式子的右端都有意义，那么

(2)

2)有波爆破的现象.本文所说的波爆破是Whitham在文献[3]中给的定义：u(x,t)本身有界，而其一阶导数在有限时间内爆破(即‖ux(5,t)‖L∞→∞,t→T).显然，KdV方程也是浅水波方程，但没有波爆破现象.而波爆破是可以观察到的一个物理现象，所以从这个意义上说，Camassa-Holm方程是一个比KdV方程更合适的浅水波模型.

3)尖峰孤立波的存在性.以前的孤立子(soliton，是一种行波)大都是光滑的，但这里的孤立波是有尖峰的，如e-|x-t|,后来称之为peakon.

关于Camassa-Holm方程的数学理论研究(从方程的角度)是从1997年开始的，到现在已有16年的历史，众多数学家在这方面做了很多重要的研究工作.下面列出一些主要成果.

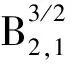
2)弱解的全局存在性.Camassa-Holm方程可以改写成如下的形式：

(3)

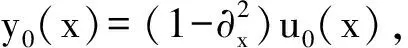
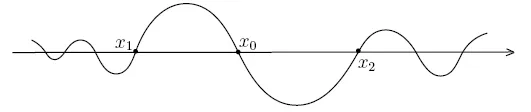
图1 y0(x)的图像

2004年，McKean[11]用反证法又给出了一个简化的证明，假设具有以上性质的初始值所对应的解全局存在，从而导出矛盾.反证法有它自身的优点，但很难让人们看清其内在的结构.基于文献[12]的工作,文献[13]用纯分析的手段重新证明了McKean的波爆破定理，让人们看清了导致解在有限时间内爆破的真正原因.

4)孤立波的轨道稳定性.Constantin等[14]在2000年用方程(1)本身的结构特点，得出了其尖峰孤立波的轨道稳定性.笔者[15]用构造泛函的方法也得到了孤立波的稳定性.

关于Camassa-Holm方程的无穷传播速度和大时间性态，分别在下面进行介绍.

2 无穷传播速度与持续一致性

抛物方程，如热传导方程，具有无穷传播的特性;而双曲方程，如波方程和双曲守恒律方程等，具有有限传播的特性.方程(1)的前2项就是一维的Burgers方程，其本身跟不可压的Euler方程也很像.所以,关于Camassa-Holm方程的传播速度问题是一个很基本、很重要的问题.或者可以问得更一般一些，给定一个具有紧支集的初始值u0(x)，其对应的强解u(x,t)具有怎样的性质呢？2007年，Himonas等[16]完全地回答了这个问题(见下面的定理).

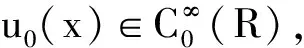
(4)

式(4)中:L(t)>0;L′(t)>0;l(t)<0;l′(t)<0;q(x,t)为特征线(粒子轨迹)满足

(5)

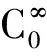
对于在无穷处具有指数衰减的初始值u0(x)，文献[16]有如下的持续一致性:

定理2[16]假设u0(x)∈Hs(R),s>3/2,u(x,t)是[0,T]上的强解，θ∈(0,1),

|u0(x)|,|u0x(x)|～O(e-θ|x|)，|x|→∞,

那么解u(x,t)在[0,T]上一致地满足

|u(x,t)|,|ux(x,t)|～O(e-θ|x|)，|x|→∞.

2012年，文献[17]对在无穷处具有代数衰减的初始值u0(x)建立了持续一致性.

3 解的大时间性态的初步研究

由McKean的定理知道,若y0(x)恒大于0(恒小于0)，或者只改变一次符号(正的在负的右边)，则Camassa-Holm方程(1)所对应的解全局存在.考虑比较简单的情况，再假设y0(x)具有紧支集，如图2(a)～(c)所示.

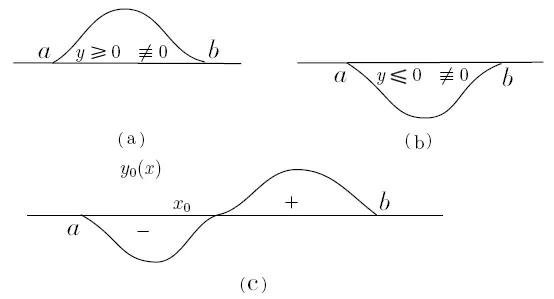
图2 具有紧支集的y0(x)的图像

根据恒等式

对于任意的时间0

方程(1)有一个基本的问题是:如果解全局存在，那么它的大时间性态如何呢？最近的文献有一个很初步的研究：只是看支集区间长度q(b,t)-q(a,t)的一个极限.

定理3[18]假设y0(x)具有紧支集，其支集在区间[a,b]内.

1)如果y0(x)≥0(≢0)(如图2(a)所示)， 那么eq(b,t)-eq(a,t)→+∞,t→+∞.

2)如果y0(x)≤0(≢0)(如图2(b)所示)，那么e-q(a,t)-e-q(b,t)→+∞,t→+∞.

3)如果存在一点x0,使得y0(x0)=0，而在(a,x0)上y0(x)≤0(≢0)，在(x0,b)上y0(x)≥0(≢0)(如图2(c)所示)，那么q(b,t)-q(a,t)→+∞,t→+∞.

注1由Camassa-Holm方程的反对称性知，定理3中的1)和2)是一样的.但是，在这两种情况下还不知道当时间t趋于无穷时q(b,t)-q(a,t)的极限.

4 一些公开问题

下面提出2个问题.

1)解在爆破时的具体形态.Camassa-Holm方程具有波爆破的性质，即u(x,t)本身是有界的，而其一阶导数ux(x,t)产生了爆破.假设u(x,t)在时刻T发生爆破，并且只有一个爆破点x0，一个有意义的问题是如何研究此刻u(x,T)作为一个一元函数的具体图像，特别是在爆破点x0附近的具体图像.比较容易得到,u(x,T)依然是一个连续函数，但具体是怎样的表现形式还不知道.例如可以问：是否存在0<α<1，使得下面的极限有意义：

如果是，那么说明u(x,T)在爆破点x0附近与一个幂函数的表现形式差不多.但对这个问题的研究目前还没有任何进展.

2)解的大时间性态.这里面有很多问题，文献[18]只是一个开端，在注1中就有一个问题没有被解决.假设Camassa-Holm方程的解全局存在，那么如下极限是否存在:

参考文献：

[1]Fuchssteiner B,Fokas A S.Symplectic structures,their Bäcklund transformations and hereditary symmetries[J].Physica D: Nonlinear Phenomena,1981,4(1):47-66.

[2]Camassa R,Holm D D.An integrable shallow water equation with peaked solitons[J].Phys Rev Lett,1993,71(11):1661-1664.

[3]Whitham G B.Linear and nonlinear waves[M].New York:Wiley-Interscience,1974.

[4]Kato T.Perturbation theory for linear operators[M].2nd ed.New York:Springer-Verlag,1976.

[5]Rodríguez-Blanco G.On the Cauchy problem for the Camassa-Holm equation[J].Nonlinear Anal:A Theory Methods,2001,46(3):309-327.

[6]Li Yi′a,Olver P J.Well-posedness and blow-up solutions for an integrable nonlinearly dispersive model wave equation[J].J Differential Equations,2000,162(1):27-63.

[7]Danchin R.A note on well-posedness for Camassa-Holm equation[J].J Differential Equations,2003,192(2):429-444.

[8]Xin Zhouping,Zhang Ping.On the weak solutions to a shallow water equation[J].Comm Pure Appl Math,2000,53(11):1411-1433.

[9]Bressan A,Constantin A.Global conservative solutions of the Camassa-Holm equation[J].Arch Ration Mech Anal,2007,183(2):215-239.

[10]McKean H P.Breakdown of a shallow water equation[J].Asian J Math,1998,2(4):867-874.

[11]McKean H P.Breakdown of the Camassa-Holm equation[J].Comm Pure Appl Math,2004,57(3):416-418.

[12]Zhou Yong.Wave breaking for a shallow water equation[J].Nonlinear Anal,2004,57(1):137-152.

[13]Jiang Zaihong,Ni Lidiao,Zhou Yong.Wave breaking of the Camassa-Holm equation[J].J Nonlinear Sci,2012,22(2):235-245.

[14]Constantin A,Strauss W.Stability of peakons[J].Comm Pure Appl Math,2000,53(5):603-610.

[15]Zhou Yong.Stability of solitary waves for a rod equation[J].Chaos Solitons Fractals,2004,21(4):977-981.

[16]Himonas A,Misiolek G,Ponce G,et al.Persistence properties and unique continuation of solutions of the Camassa-Holm equation[J].Comm Math Phys,2007,271(2):511-522.

[17]Ni Lidiao,Zhou Yong.A new asymptotic behavior of solutions to the Camassa-Holm equation[J].Proc Amer Math Soc,2012,140(2):607-614.

[18]Jiang Zaihong,Zhou Yong,Zhu Mingxuan.Large time behavior for the support of momentum density of the Camassa-Holm equation[J].J Math Phys,2013,54(8):081503.