不含4-和5-圈的平面图的均匀染色*

王维凡, 桂 浩

(浙江师范大学 数理与信息工程学院,浙江 金华 321004)

0 引 言

本文所指的图均为有限的、无向的简单图.给定一个图G,分别用V(G),E(G),|G|,δ(G),Δ(G)(简记为Δ)表示G的顶点集合、边集合、阶、最小度和最大度.一个图G的顶点k-染色是指V(G)到颜色集合{1,2,…,k}的一个映射φ,使得任意2个相邻的顶点x和y满足φ(x)≠φ(y);G的色数χ(G)定义为使得G有k-染色的最小整数k;给定G的一个k-染色φ,用Vi表示染颜色i的顶点集合;如果对任一对i, j∈{1,2,…,k}有||Vi|-|Vj||≤1,那么就称φ为G的均匀染色,或者G是均匀k-可染的;图G的均匀色数定义为: χe(G)=min{k | G是均匀k-可染的}.

显然, χe(G)≥χ(G),且不等式可以严格成立.1973年,Meyer[1]引进了图的均匀染色的概念,并提出以下猜想:

猜想1若G不是完全图也不是奇圈,则χe(G)≤Δ.

1970年,Hajnal等[2]证明了对于k≥Δ+1,任意一个最大度为Δ的图G都是均匀k-可染的;文献[3]应用算法分析给出了一个新的且短的证明;1994年,文献[4]提出以下猜想：

猜想2[4]如果一个连通图G不是Km,C2m+1和K2m+1,2m+1(m≥1),那么图G是均匀Δ-可染的.

文献[4]证明了猜想2对Δ≤3的图成立;文献[5]证明了猜想2对Δ=4的图也成立.此外,猜想2还被证明对下面特殊图类成立:树[6]、 二部图[7]、外平面图[8]及Δ≥14d+1的d-退化图[9]等.这里,如果G的每一个导出子图H包含一个度至多为d的顶点,那么就称图G为d-退化的.文献[10]证明了猜想2对于Δ≥13的平面图是成立的;文献[11]将这个结果改进到Δ≥9的情形.因此,对于平面图族,仅剩下5≤Δ≤8的情形没有解决.文献[12]证明了:Δ≥7且没有4-,5-圈的平面图满足猜想2;文献[13]证明了围长大于或者等于5的平面图满足猜想2.

本文旨在改进文献[12]中的结果,将证明:每一个5≤Δ≤6且没有4-,5-圈的平面图满足猜想2.本文的结果和文献[4-5,12]中的结果隐含着猜想2对所有没有4-,5-圈的平面图成立.

1 结构引理

在给出2个结构引理之前,需要引进一些记号和术语.设G是一个嵌入在平面上的图;用F(G)表示G的面集合;对x∈V(G)∪F(G),用d(x)表示v在G中的度;一个度为k(至少k)的点(或面)被称为k-点(或面)和k+-点(或面);用NG(v)表示一个顶点v在G中邻点的集合;对i≥1,用ni(v)表示与v相邻的i-点的个数,ni(G)表示G中i-点的个数.此外,用mk(v)表示与v关联的k-面的个数,k≥3.G的一个以u1,u2,u3为边界点的3-面记作[u1u2u3].特别地,当d(ui)=ai(i=1,2,3)时,记此面为(a1,a2,a3)-面.

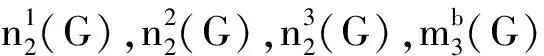
引理1若G是一个Δ=6,|G|≥5且没有4-和5-圈的连通的平面图,则G包含图1中的子图形之一.

证明 反证法.假设G不含H1～H12中的任何一个.因为G是连通的且|G|≥5,所以δ(G)≥1.将图G嵌入到平面上,则有以下断言：

断言11)n1(G)≤2.如果n1(G)=2,那么n2(G)=0.

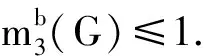
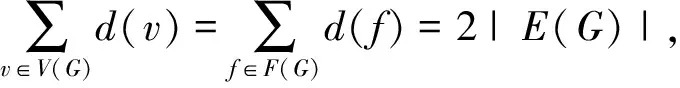
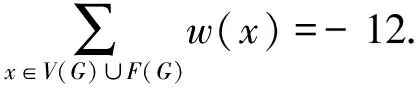
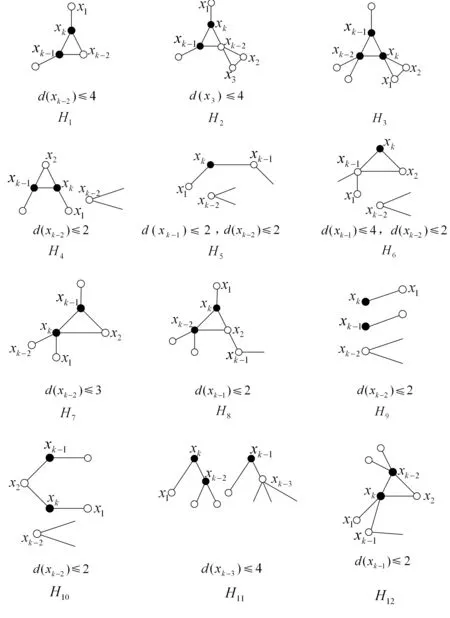
图1 引理1中的子图形H1～H12

下面将设计一个恰当的权转移规则,按照此规则重新分配点和面的权,从而得到一个新的权函数w′.而权转移前后所有点和面的权的总和是保持不变的.

注1在图1和下面的图2中,实心点的度数与图中显示的度数相同,空心点可以同图中以外的点相连.在每一个子图形中,所有标有xi的点都是不重合的.

设v是一个d(v)≥4的顶点.权转移规则定义如下:

R0:v给每一个相邻的好2-点转权1.

R1:若d(v)=4,则v平分剩余的权2-n2(v)给相关联的3-面.

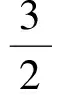
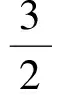
因为G不含4-圈和5-圈,且G不含4-,5-面和相邻3-面,所以下面断言成立:

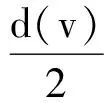
设w′表示在执行规则R0～R3之后的结果权函数.对任何x∈V(G)∪F(G),计算w′(x)的值.

首先,设 f∈F(G),那么d(f)≥3.由上面分析知,d(f)≠4和5.若d(f)≥6,则w′(f)=w(f)=d(f)-6≥0.假设d(f)=3,且设f=[xyz]满足d(x)≤d(y)≤d(z),那么d(x)≥2,d(z)≤6.

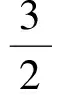
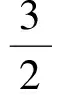
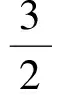
若d(x)≥5,则由规则R2和R3知,w′(f)≥-3+351=0.

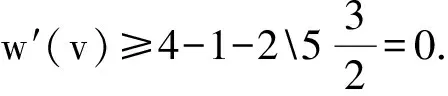
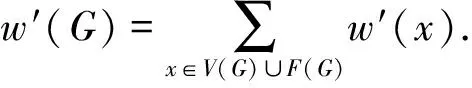
1)n1(G)=2.

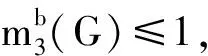
2)n1(G)≤1.

由断言1的2),并注意到Ⅱ-坏点是成对出现的,可分下面几种子情形:

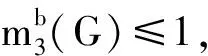
由断言1中的3),并注意到Ⅰ-坏点也是成对出现的,进一步有下面子情形:

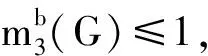
综上，总可推出下面矛盾:

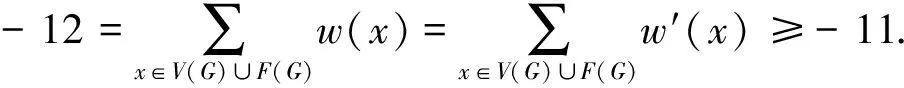
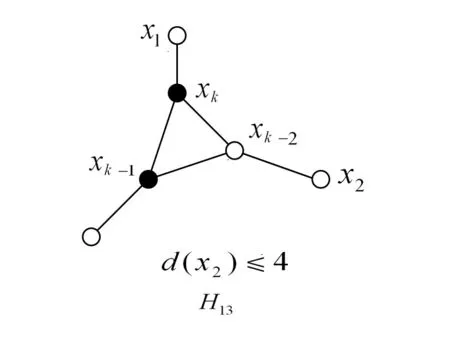
图2 引理2中的子图形 H13

引理1证毕.

类似地,可以证明下面引理：

引理2若G是一个Δ=5,|G|≥5且没有4-和5-圈的连通的平面图,则G包含H1,H3～H12和如图2所示的子图形H13.

2 主要结果

引理3[14]没有5-圈的平面图是3-退化的.

引理4[2]对k≥Δ+1,任意最大度为Δ的图G是均匀k-可染的.

引理5设G=G1∪G2满足V(G1)∩V(G2)=Ø.若G1和G2是均匀k-可染的,则G也是均匀k-可染的.

引理6[12]设S={v1,v2,…,vk}是G的顶点子集,且v1,v2,…,vk互不相同.若G-S是均匀k-可染的,且对每一个1≤i≤k有|NG(vi)-S|≤k-i,则G也是均匀k-可染的.

定理1若G是一个Δ=5,且没有4-和5-圈的平面图,则对任意的k≥5,G是均匀k-可染的.

证明 由引理4知,只需证明G是均匀5-可染的.对G的阶进行归纳证明.若|G|≤5,则结论显然成立.假设|G|≥6.若G中的每个连通分支都至多只有4个顶点,则Δ≤3.由引理4和引理5知,G是均匀5-可染的.否则,G有一个连通分支的阶至少为5.由引理2知,G包含子图形H1,H3～H12,H13之一(如图1和图2所示).令k=5,选取子集合S如下:

若G包含Hi,i∈{3,4,6,7,8,10,11,12,13},则令S={x1,x2,x3,x4,x5}.

若G包含Hi,i∈{1,5,9},则令S={x1,x2,x3,x4,x5}.其中,x2为G-{x1,x3,x4,x5}中一个度至多为3的顶点.由引理3知,x2一定存在.

容易验证上面定义的S满足:对每一个1≤i≤k,有|NG(vi)-S|≤k-i.设H=G-S,则H是一个没有4-圈和5-圈的平面图,Δ(H)≤Δ=5.若Δ(H)≤4,则由引理4知,H是均匀5-可染的.若Δ(H)=5,则由引理5和归纳假设知,H也是均匀5-可染的.总之,H有一个均匀5-染色.由引理6知,G是均匀5-可染的.定理1证毕.

定理2若G是一个Δ=6,且没有4-和5-圈的平面图,则对任意的k≥6,G是均匀k-可染的.

证明 由引理4知,只需证明G是均匀6-可染的.对G的阶进行归纳证明.若|G|≤6,则结论显然成立.假设|G|≥7.若G中的每个连通分支都至多只有5个顶点,则Δ≤4.由引理4和引理5知,G是均匀6-可染的.否则,G有一个连通分支的阶至少为6.由引理1知,G包含子图形H1～H12之一,如图1所示.令k=6,由引理6知,只需选取子集合S如下:

若G包含H2,则令S={x1,x2,…,x6}.

若G包含Hi,i∈{3,4,6,7,8,10,12},则令S={x1,x2,…,x6}.其中,x3为G-{x1,x2,x4,x5,x6}中一个度至多为3的顶点;

若G包含H11,则令S={x1,x2,…,x6}.其中,x2为G-{x1,x3,x4,x5,x6}中一个度至多为3的顶点.

若G包含Hi,i∈{1,5,9},则令S={x1,x2,…,x6}.其中,x2是G-{x1,x4,x5,x6}中度至多为3的顶点,x3是G-{x1,x2,x4,x5,x6}中度至多为3的顶点.由引理3知,x2,x3存在.定理2证毕.

定理1、定理2和文献[4-5,12]中的结果蕴含着下面定理:

定理3每一个没有4-和5-圈的平面图是均匀Δ-可染的.

参考文献：

[1]Meyer W.Equitable coloring[J].Amer Math Monthly,1973,80(8):920-922.

[2]Hajnal A,Szemeréi E.Proof of a conjecture of Erdös[J].Combinatorial Theory and Its Applications,1970,2:601-623.

[3]Kierstead A,Kostochka A,Mydlarz M,et al.A fast algorithm for equitable coloring[J].Combinatorica,2010,30(2):217-224.

[4]Chen B L,Lih K W,Wu Poulin.Equitable coloring and the maximum degree[J].European J Combin,1994,15(5):443-447.

[5]Kierstead A,Kostochka A.Every 4-colorable graph with maximum degree 4 has an equitable 4-coloring[J].J Graph Theory,2012,71(1):31-48.

[6]Chen B L,Lih K W.Equitable coloring of trees[J].J Combin Theory Ser B,1994,61(1):83-87.

[7]Lih K W,Wu Poulin.On equitable coloring of bipartite graphs[J].Discrete Math,1996,151(1/2/3):155-160.

[8]Kostochka A V.Equitable colorings of outerplanar graphs[J].Discrete Math,2002,258(1/2/3):373-377.

[9]Kostochka A V,Nakprasit K,Pemmaraju S V.Equitable colorings ofk-degenerate graphs[J].Combin Probab Comput,2006,19(1):53-60.

[10]Zhang Yi,Yap H P.Equitable colorings of planar graphs[J].J Combin Math Combin Comput,1998,27(1):97-105.

[11]Nakprasit K.Equitable colorings of planar graphs with maximum degree at least nine[J].Discret Math,2012,312(5):1019-1024.

[12]Zhu Junlei,Bu Yuehua.Equitable list colorings of planar graphs without short cycles[J].Theoret Comput Sci,2008,407(1/2/3):21-28.

[13]Nakprasit K,Nakprasit K.Equitable colorings of planar graphs without short cycles[J].Theoret Comput Sci,2012,465:21-27.

[14]Wang Weifan,Lih K W.Choosability and edge choosability of planar graphs without five cycles[J].Appl Math Lett,2002,15(5):561-565.