沉垫自升式平台迁移工况桩腿力学研究

徐兴平，张 棣，张 辛，王言哲，刘 松

(1.中国石油大学机电工程学院,山东青岛266580；2.中石化胜利石油工程有限公司海洋钻井公司,山东东营257000)

带有储油沉垫的自升式平台集开采、处理、存储功能为一体,适合于边际油田的开发[1-3]。在平台迁移过程中,桩腿会受到风力、重力和惯性力的作用[4],使桩腿承受极大的弯矩。研究沉垫自升式平台迁移工况桩腿弯矩时,除考虑普通自升式平台[5-6]桩腿所受弯矩之外,还应考虑沉垫的影响。潘斌等[7]从平台稳定性的角度研究了沉垫对平台抗风能力的影响,滕晓青等[8]研究了沉垫位置对平台桩腿受力的影响。安军、郝林[10-11]对平台横摇加速度进行分析,研究了普通自升式平台迁移工况桩腿受力情况。笔者根据沉垫自升式平台迁移工况下桩腿的受力情况,推导桩腿惯性弯矩及总弯矩公式,研究沉垫位置与桩腿弯矩的关系。自升式平台的设计工况包括：作业工况、迁移工况、升降工况和自存工况。平台迁移一般分油田内迁移和远洋迁移[9]两种工况。迁移工况下平台桩腿强度的校核主要包括：平台在自振周期下纵摇或横摇产生的惯性弯矩、风载荷作用于桩腿产生的风压弯矩、桩腿自重产生的静弯矩。CCS规范[9]中规定,桩腿总弯矩可按周期10 s,单边横摇摆幅15°或单边纵摇摆幅15°时的弯矩及平台在相应倾角时重力弯矩的120%求得。笔者按照平台单边横摇摆幅15°、周期10 s的工况对桩腿弯矩进行研究。

1 迁移工况桩腿弯矩

平台迁移工况下横摇力学模型如图1所示。

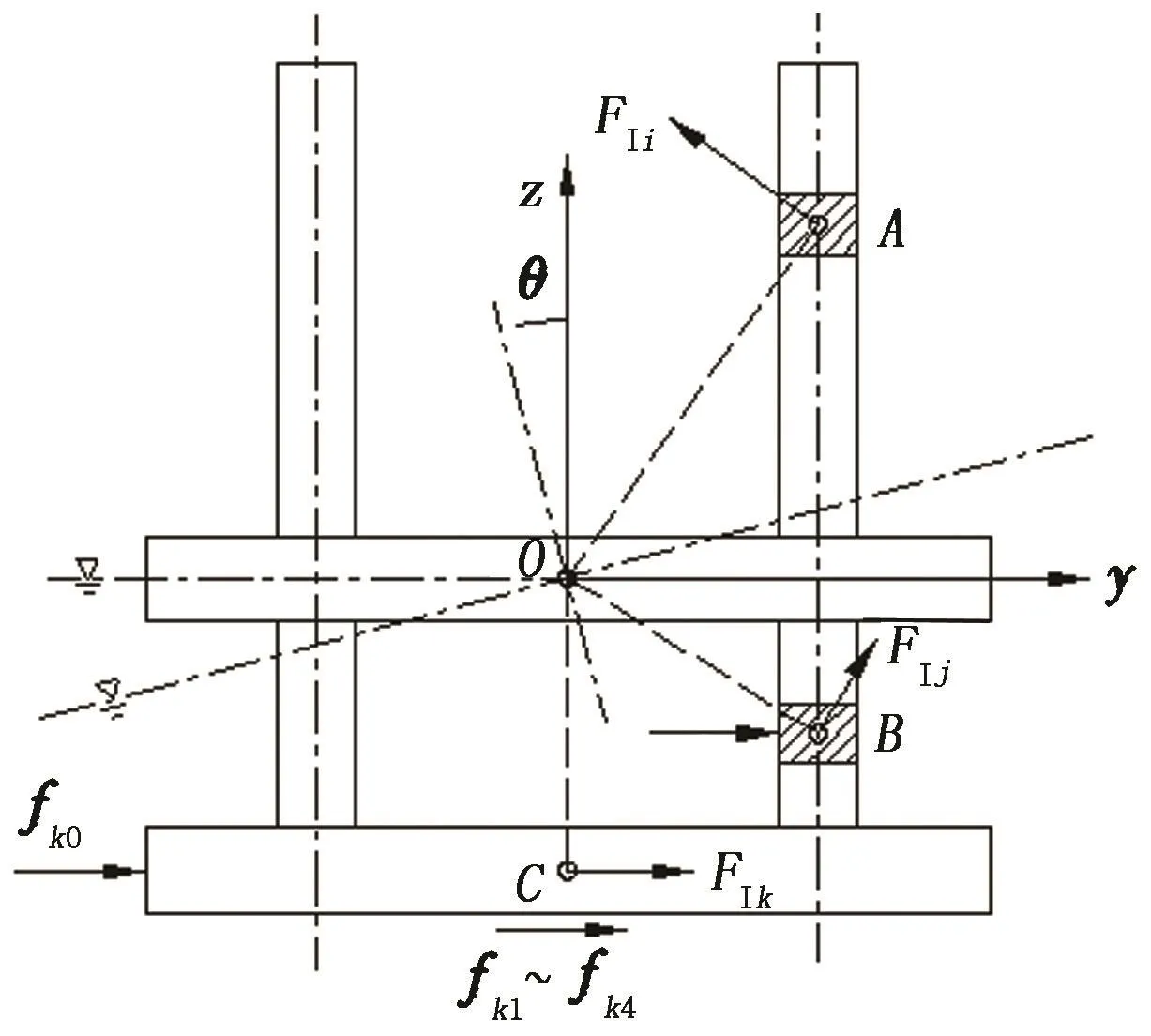
图1 平台迁移过程横摇力学模型示意图Fig.1 Sketch map of rolling force model of jack up platform under towing

图中,z轴正方向竖直向上,y轴正方向为水平方向,O为坐标原点,且为平台横摇中心,A为主甲板以上桩腿任意质量单元形心,B为主甲板以下桩腿任意质量单元形心,C为沉垫形心。记主甲板以上桩腿任意质量单元i的自重为Wi(kg),惯性力为FIi(N)；主甲板以下桩腿任意质量单元j的自重为Wj(kg),惯性力为FIj(N)；沉垫自重为Wk(kg),惯性力为FIk(N)。记主甲板以下桩腿任意质量单元j所受海水阻力为fj(N),沉垫垂直于自身运动方向的表面所受海水阻力为fk0,沉垫平行于自身运动方向的上、下、前、后4个表面所受海水阻力为fk1～fk4。

假设平台迁移过程中的横摇为简谐运动,则横摇角θ为

式中,η为平台横摇摆幅,m；ω为平台横摇运动的频率,1/s。

对式(1)求二次导数,可得平台横摇角加速度a为

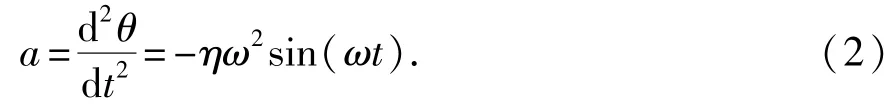
当平台横摇至极限位置(θ最大)时,角速度为零,角加速度a最大,表示为

1.1 普通自升式平台桩腿弯矩

对于普通自升式平台[10-11],主甲板以上桩腿任意质量单元因横摇加速度引起的惯性力为

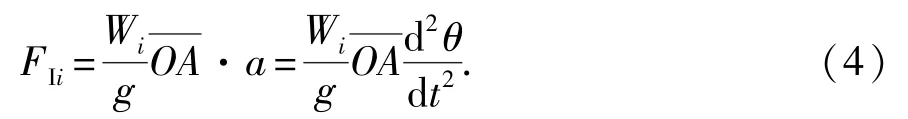
惯性力FIi可分解为垂直于桩腿的力HIi和平行于桩腿的力VIi,VIi不对桩腿产生弯矩。质量单元i与y轴的距离记为zi。

质量单元i在主甲板处的惯性弯矩为Mli,质量单元j在主甲板处的惯性弯矩为Mlj,j与y轴的距离记为zj,则总惯性弯矩MI为

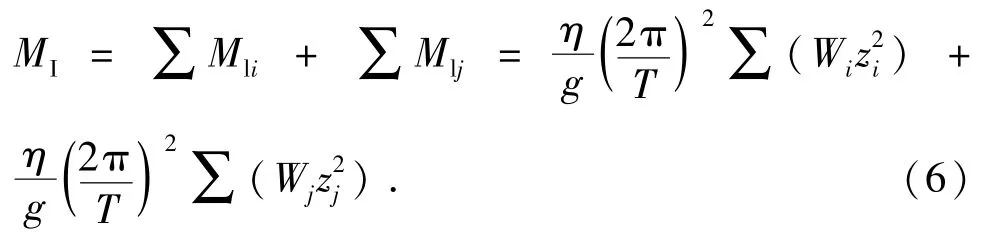
风力产生的弯矩为MF,自重产生的弯矩为Mg,则桩腿在主甲板处的总弯矩MO为

1.2 沉垫自升式平台桩腿弯矩

与普通自升式平台不同,沉垫的存在导致平台迁移过程中的横摇运动发生变化。虽然沉垫及主甲板以下桩腿的重力可以通过沉垫舱压载调节,但它们的惯性力和运动阻力是无法避免的,在计算桩腿弯矩时必须考虑。

假设平台迁移中的横摇仍为简谐运动,O为横摇中心,则平台横摇角加速度a为

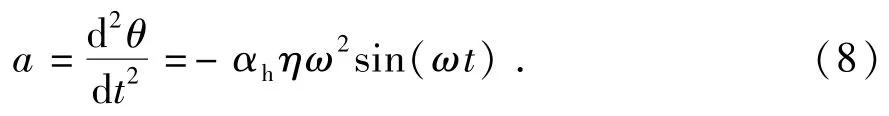
式中,αh为沉垫及主甲板以下桩腿的惯性力和运动阻力对横摇幅度的影响系数。

桩腿在主甲板处的总弯矩M′O为

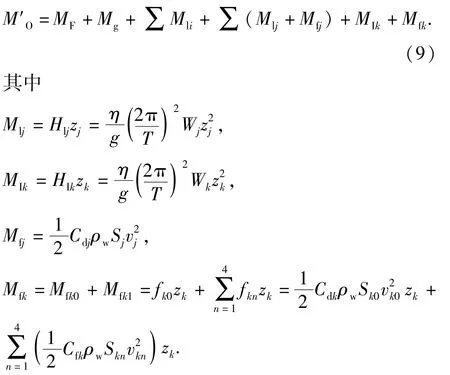
式中,Mlj、MIk、Mfj和Mfk分别为主甲板以下桩腿在主甲板处的惯性弯矩、沉垫在主甲板处的惯性弯矩、主甲板以下桩腿在主甲板处的海水阻力弯矩和沉垫在主甲板处的海水阻力弯矩；zk为沉垫形心与y轴的距离。

当平台横摇至极限位置(θ最大)时,角加速度和惯性力均最大,此时角速度为零,故桩腿及沉垫围绕浮心O的横摇线速度为零。根据式(9),此时沉垫及主甲板以下桩腿所受海水阻力为零。故平台横摇至极限位置时,桩腿在主甲板处的总弯矩M′O为

2 沉垫位置对桩腿弯矩的影响

2.1 桩腿惯性弯矩

对沉垫自升式平台做两点假设：

①主甲板及桩腿与相同型号普通自升式平台完全相同；

②主甲板以下桩腿和沉垫的自重通过沉垫舱压载调节至平衡。

基于上述假设,对比式(7)、(10),无沉垫和有沉垫两种情况下,平台横摇至极限位置时桩腿总弯矩的主要区别在于总惯性弯矩。沉垫自升式平台桩腿在主甲板处的总惯性弯矩M′I为

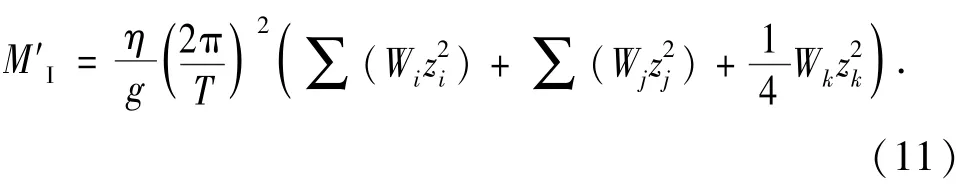
根据式(6)、(8),总惯性弯矩M′I亦可表示为

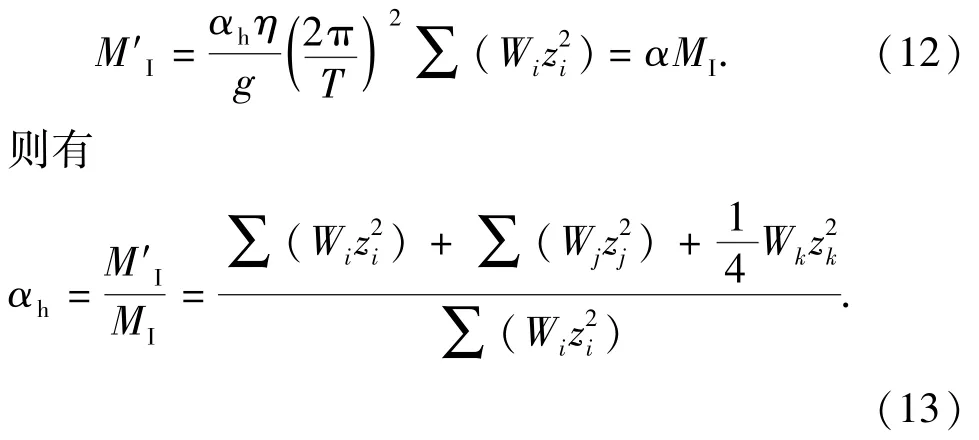
在桩腿上均匀地选取质量单元i、j,则有Wi=Wj,式(13)可改写为

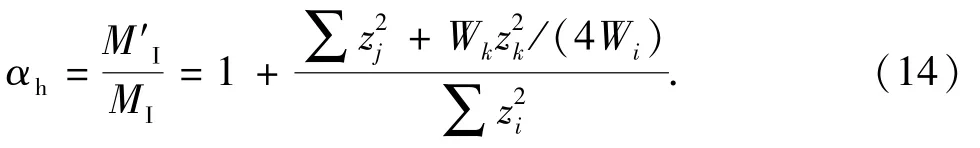
对式(14)进行分析：

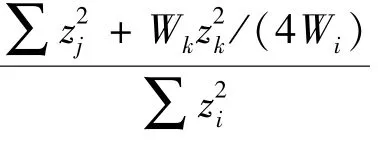
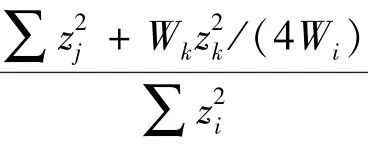
2.2 桩腿总弯矩分析

根据公式(10)、(14),沉垫自升式平台桩腿在主甲板处的总弯矩为

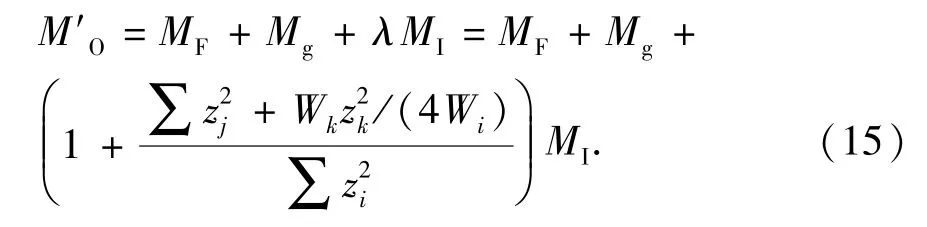
风力作用于桩腿产生的弯矩MF为

自重作用于桩腿产生的弯矩Mg为

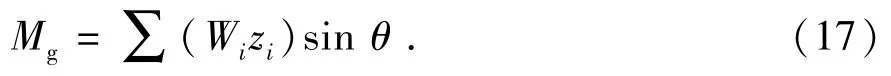
将式(16)、(17)带入式(15),则桩腿在主甲板处的总弯矩为

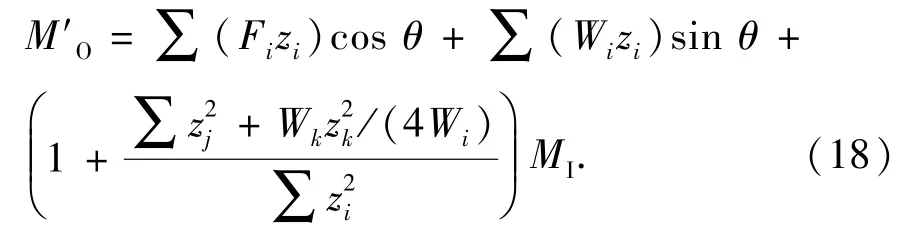
将式(6)带入式(18),经整理有

zi、zj、zk由沉垫位置决定,它们之间的关系如下：

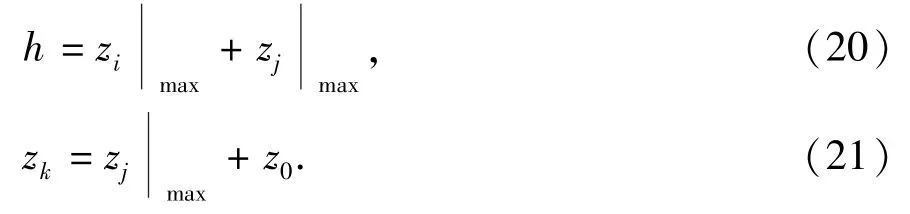
式中,h为桩腿总高度；z0为沉垫形心至沉垫上表面的距离。

分析式(19) ～ (21) 可知,zi、zj、zk存在一一对应的关系,桩腿在主甲板处的总弯矩与沉垫位置的关系可以通过主甲板以上桩腿的长度表示,也可以通过沉垫形心与y轴的距离zk表示。

3 平台实例计算

3.1 平台参数

将平台桩腿等分为30节,沉垫与主甲板各占两节。当沉垫紧靠主甲板时,主甲板以上桩腿最长,此时有i=26(即imax=26),约为98 m。平台主要尺寸参数如下：

主甲板(长L1×宽B1×高H1)：60 m×45 m×7.54 m；沉垫(长L2× 宽B2× 高H2)：60 m ×40 m ×7.54 m；桩腿长度L：133 m；水深H：80 m；桩腿节距hi：3.77 m；主弦管中心距a：10 m；主弦管(长度l1×外径d1× 壁厚δ1)：3.77 m ×0.4 m ×0.04 m；水平外撑(长度l2×外径d2×壁厚δ2)：10 m×0.2191 m×0.018 m；水平内撑(长度l3×外径d3×壁厚δ3)：5 m×0.1683 m×0.018 m；斜撑(长度l4×外径d4× 壁厚δ4)：6.26 m ×0.2191 m ×0.018 m。

平台桩腿侧面及横截面型式如图2所示。

3.2 桩腿自重与沉垫自重

对桩腿以节距为单位进行分析,根据表1及图2所示桩腿结构进行计算,每节的自重为

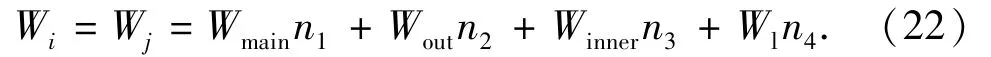
式中,n1、n2、n3、n4分别为每节桩腿中主弦管、水平外撑、水平内撑、斜撑的数量。

图2 平台桩腿侧面及横截面型式Fig.2 Side and cross section of platform leg

对于沉垫自重Wk,通过压载调节使沉垫悬浮于水中,则沉垫自重应包括沉垫本身重力以及压载水重力,并且与沉垫排开海水的重力相同。

3.3 桩腿风力

风力计算按照CCS规范中平台远洋迁移的设计风速进行计算,本例中设计风速取36 m/s。桩腿所受风力[9]为

式中,S为受风面积,m2；Ch为受风构件高度系数,随着高度的增加而增加,从海面以上高度0～15.3 m时的1.00增加到海面以上高度91.5～106.5 m时的1.48,具体数值可查阅参考文献[9]；Cs为受风构件形状系数。根据CCS规范,桁架式桩腿的受风面积近似地取每侧满实投影面积的30%,形状系数取1.3。

3.4 沉垫自升式平台桩腿弯矩

平台横摇最大倾角15°、周期10 s,对沉垫在不同位置时桩腿弯矩进行计算,得到桩腿弯矩与主甲板以上桩腿长度的关系,如图3、4所示。

图3 风力、重力弯矩与主甲板以上桩腿长度关系Fig.3 Relationship between length of leg above main deck and bending moments from wind and gravity

由图3、4可知,沉垫自升式平台迁移过程中风力、重力产生的弯矩均随着主甲板以上桩腿长度的增加而增大。由于沉垫的影响,随着主甲板以上桩腿长度增加,沉垫距离主甲板越来越近,惯性弯矩逐渐减小。特别地,由图4可知,总惯性弯矩与总弯矩的值非常接近,总惯性弯矩是总弯矩变化的决定因素,风力、重力产生的弯矩无法影响总弯矩的走势。由此可知,迁移工况下,平台摇晃产生的惯性弯矩是桩腿强度校核时应考虑的主要因素。

图4 总惯性弯矩、总弯矩与主甲板以上桩腿长度关系Fig.4 Relationship between length of leg above main deck and total inertia bending moment and total bending moment

M′O(i-1)-M′O(i)为沉垫每下降一节桩腿的距离时桩腿总弯矩的增加值(图5)。由图5可知,imax=26时,沉垫最靠近主甲板,沉垫下降一个桩腿节距的距离,桩腿总弯矩的上升幅度最小；imax=2时沉垫距主甲板较远,此时沉垫下降一个桩腿节距的距离,桩腿在主甲板处总弯矩的上升幅度最大。

图5 沉垫位置不同时的M′O(i-1)-M′O(i)值Fig.5 Value of M′O(i-1)-M′O(i)as mat fixed in different places

从imax=26开始,沉垫每下降单位距离,桩腿总弯矩的上升幅度呈线性变化。

综合分析图4、5可知,平台迁移过程中,因平台稳性、天气情况或其他原因须降低沉垫位置时,imax可在20～26之间调节,因为这一区间桩腿总弯矩的变化不大。

对于本例中的平台,imax≤10时,桩腿总弯矩及其上升幅度都比较大。平台迁移过程中不会将沉垫放至如此低的位置,但是对于平台就位之后的沉垫、桩腿下放过程有参考意义。为减小这一区间内桩腿的总弯矩,应选择天气条件较好的时间对平台进行就位放桩作业。

3.5 普通自升式平台桩腿弯矩

为与沉垫自升式平台进行比较,依据普通自升式平台桩腿在主甲板处的总弯矩计算公式(7),取各尺寸参数均相同的普通自升式平台进行桩腿弯矩分析。桩腿位置不同时所得弯矩结果如图6所示。

图6 普通自升式平台桩腿位置不同时弯矩与其长度关系Fig.6 Relationship between length of leg above main deck and total inertia bending moment and total bending moment of ordinary jack up platform

由图6可知,与沉垫自升式平台不同,普通自升式平台迁移过程中,惯性弯矩、总弯矩均随着主甲板以上桩腿长度的减小而呈现先减小后增大的趋势。主甲板以上桩腿长度较大时,风力产生的弯矩对总弯矩的影响较大。由此可见,迁移工况下,对于普通自升式平台来说,惯性弯矩及风力弯矩均是桩腿强度校核时应考虑的主要因素。

4 结 论

(1)沉垫的存在会增大桩腿在主甲板处的惯性弯矩。主甲板以上桩腿长度减小,沉垫与主甲板的距离增大,则风力、重力产生的弯矩减小,惯性弯矩增大。惯性弯矩是总弯矩变化的决定因素。

(2)沉垫每下降单位距离,桩腿总弯矩的上升幅度呈线性变化。沉垫在靠近主甲板位置时,桩腿总弯矩变化不大,可以根据拖航稳性需要来降低沉垫位置。

(3)普通自升式平台迁移过程中,惯性弯矩、总弯矩均随主甲板以上桩腿长度的减小而呈现先减小后增大的趋势。主甲板以上桩腿长度较大时,风力对总弯矩影响较大。

[1] MARK J K.Marginal production in the Gulf of Mexico—I：historical statistics&model framework[J].Applied Energy,2010,87：2535-2550.

[2] WANG Hui,HU Guangyi,FAN Hongjun,et al.Key technologies for the fluvial reservoir characterization of marginal oil fields[J].Petroluem Exploration and Development,2012,39(5)：667-673.

[3] 周宝勇,余建星,杜尊峰,等.边际油田开发新型平台及水下储油研究[J].海洋技术,2010,29(4)：71-75.ZHOU Baoyong,YU Jianxing,DU Zunfeng,et al.Research on new platform and underwater oil storage for marginal oil field development[J].Ocean Technology,2010,29(4)：71-75.

[4] JO C H,KIM K S,LEE S H.Parametric study on offshore jacket launching[J].Ocean Engineering,2002,29：1959-1979.

[5] 李红涛,汪震宇.拖航状态下自升式钻井平台桩腿结构强度分析[J].中国海洋平台,2012,27(4)：10-14.LI Hongtao,WANG Zhenyu.Research on leg structure analysis for self-elevating drilling units under transit condition[J].China Offshore Platform,2012,27(4)：10-14.

[6] 尹秀凤,刘静,李磊,等.拖航工况自升式平台桩腿结构强度计算分析[J].船海工程,2013,42(2)：100-102.YIN Xiufeng,LIU Jing,LI Lei,et al.Structural strength analysis of jack up leg in transit condition[J].Ship&O-cean Engineering,2013,42(2)：100-102.

[7] 潘斌,刘震,卢德明.自升式平台拖航稳性研究[J].海洋工程,1996,14(3)：15-20.PAN Bin,LIU Zhen,LU Deming.Research of the jackup platform stability in towing condition[J].The Ocean Engineering,1996,14(3)：15-20.

[8] 滕晓青,顾永宁.沉垫型自升式平台拖航状态强度分析[J].上海交通大学学报,2000,34(12)：1723-1727.TENG Xiaoqing,GU Yongning.Strength analysis of the mat supported jack up platform in transit condition[J].Journal of Shanghai Jiaotong University,2000,34(12)：1723-1727.

[9] 中国船级社.海上移动式平台入级与建造规范[M].北京：人民交通出版社,2012.

[10] 安军.在役自升式平台拖航过程桩腿强度评估[D].天津：天津大学建筑工程学院,2009.AN Jun.The evaluation of the strength in the transition condition for the jack-up platform's legs in service[D].Tianjin：School of Civil Engineering,Tianjin University,2009.

[11] 郝林.自升式平台迁移过程桩腿静态和动态强度分析[D].天津：天津大学建筑工程学院,2007.HAO Lin.The analysis of the static and dynamic strength for the jack-up platform's legs in the transition condition[D].Tianjin：School of Civil Engineering,Tianjin University,2007.