函数关系已知的混沌系统的广义外同步

宁 娣

(中南民族大学 数学与统计学学院，武汉 430074)

混沌同步在生物、化学、医学和信息科学领域具有良好的应用前景， 自Pecora和Carroll提出了一种混沌同步方法以来[1-3]，混沌同步受到越来越多的关注，随之也出现了各种各样的同步方法，如驱动响应法，变量耦合法，自适应法，变量反馈法等[4-6].

目前所研究的同步主要包含两种：一种是系统内部的同步，即所有状态均稳定到系统的平衡态；另一种是两个系统之间的同步，称之为外同步.具体来说，两个系统节点动力学完全相同的同步称之为完全同步，但就实际情况而言，参数失配和各种失真总是存在且不可避免，所以在现实系统中难以产生两个完全相同的混沌系统.为此，人们提出了“广义同步”的概念，即两个系统节点动力学不同的同步称之为广义同步，它比完全同步有更宽广的应用前景.

广义同步，即在主从混沌系统之间建立一种函数关系，这种函数关系可能已知，也可能未知.当函数关系已知，可以通过自适应控制器的方法设置控制器使主从系统满足给定的函数关系[7-9].本文在函数关系已知的情况下，研究了参数未知且动力学不同的两个系统的同步，并从数值仿真的角度验证了理论的存在性，并把函数关系形象地表示出来.

1 理论推导

考虑如下数学模型描述的两个非线性动力系统，分别作为驱动系统和响应系统：

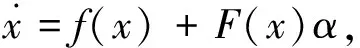
(1)

(2)

其中x=(x1,x2,…，xn)T∈Rn，y=(y1,y2,…，ym)T∈Rm分别为驱动系统和响应系统的状态向量，f∈Rn，g∈Rm分别为驱动和响应系统的非线性项，F∈Rn×l，G∈Rm×s为连续的向量函数，α∈Rl，β∈Rs为系统的未知参数向量，u(x,y)为输入控制器.

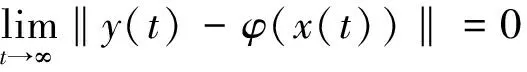
假设1(全局Lipschitz条件) 假设存在一常数L≥0，使得对于任意的x(t),y(t)∈Rn，有‖g(x(t))-g(y(t))‖≤L‖x(t)-y(t)‖.

这里‖·‖是2-范数.

当函数关系φ:Rn→Rm已知，可以得到下面的定理1.

定理1 假定假设1成立，且控制器满足：

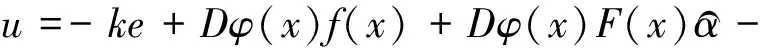
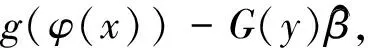
(3)

以及参数自适应律满足：

(4)

(5)

则驱动系统(1)和响应系统(2)达到广义外同步.

这里r1，r2是正常数.

证明定义系统(1)和(2)的误差为e=y-φ(x)，所以得到误差系统为：

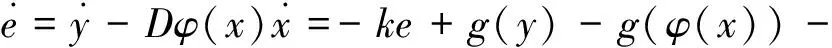
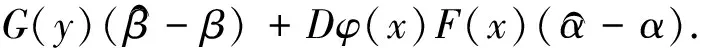
(6)

构造Lyapunov函数：

将(4)、(5)式代入误差系统(6)可得：

2 线性关系下的Lorenz与Chen系统的广义外同步

在这部分中，我们用Lorenz系统[10]和Chen系统[11]来验证上述理论的正确性，这里考虑的两个系统，分别是经典的Lorenz系统和Chen系统，且两个系统的参数均未知.

Lorenz系统：

其中α=(a,b,c)T是未知参数.因为Lorenz系统是混沌的，所以状态变量xi(i=1,2,3)是有界的，如图1所示，其中参数为a=10,b=8/3,c=28.

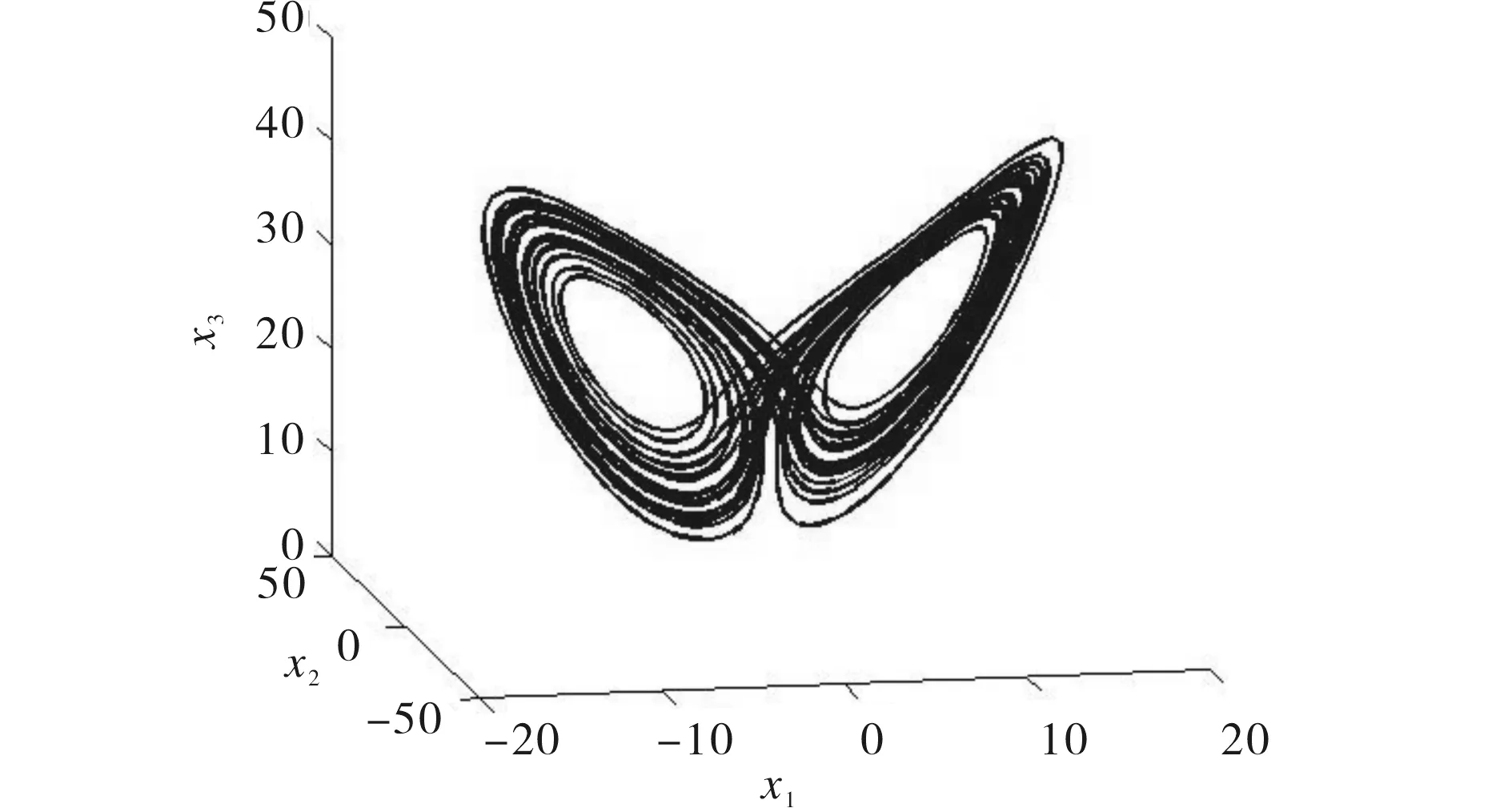
图1 Lorenz吸引子的相图Fig.1 Phase diagram of the Lorenz attractor

经典的Chen系统如图2所示，其中参数为l=35,m=3,n=28.对应的常微分方程组如下：

其中β=(l,m,n)T是未知参数.

图2 Chen吸引子的相图Fig.2 Phase diagram of the Chen attractor

这里，我们把Lorenz系统看成是驱动系统，把Chen系统作为响应系统.为了实现Lorenz系统和Chen系统之间的广义外同步，在Chen系统上添加控制器，得到如下的系统：

这里，u=(u1,u2,u3)T是公式(3)所确定的控制器.

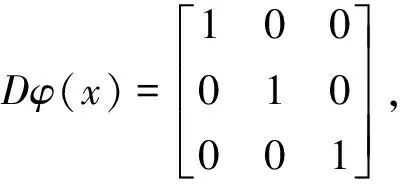
数值模拟中采用Matlab中的Ode45这个命令，随机选择混沌动力系统的初值，取常数k=200，r1=r2=10.图3和图4给出了驱动系统和响应系统满足线性关系时的相图.图5显示了驱动系统和受控响应系统的误差图，由图5可知,随着时间的增加，同步误差迅速趋向于零，即Lorenz系统和Chen系统达到广义外同步.图6给出了两个系统第一个变量之间的关系.

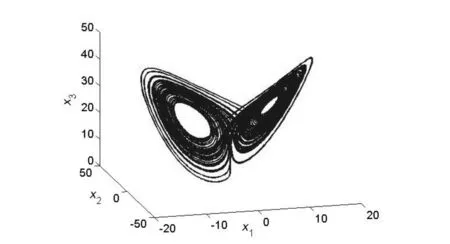
图3 线性关系下的驱动系统的相图Fig.3 Phase diagram of the drive system with linear relations

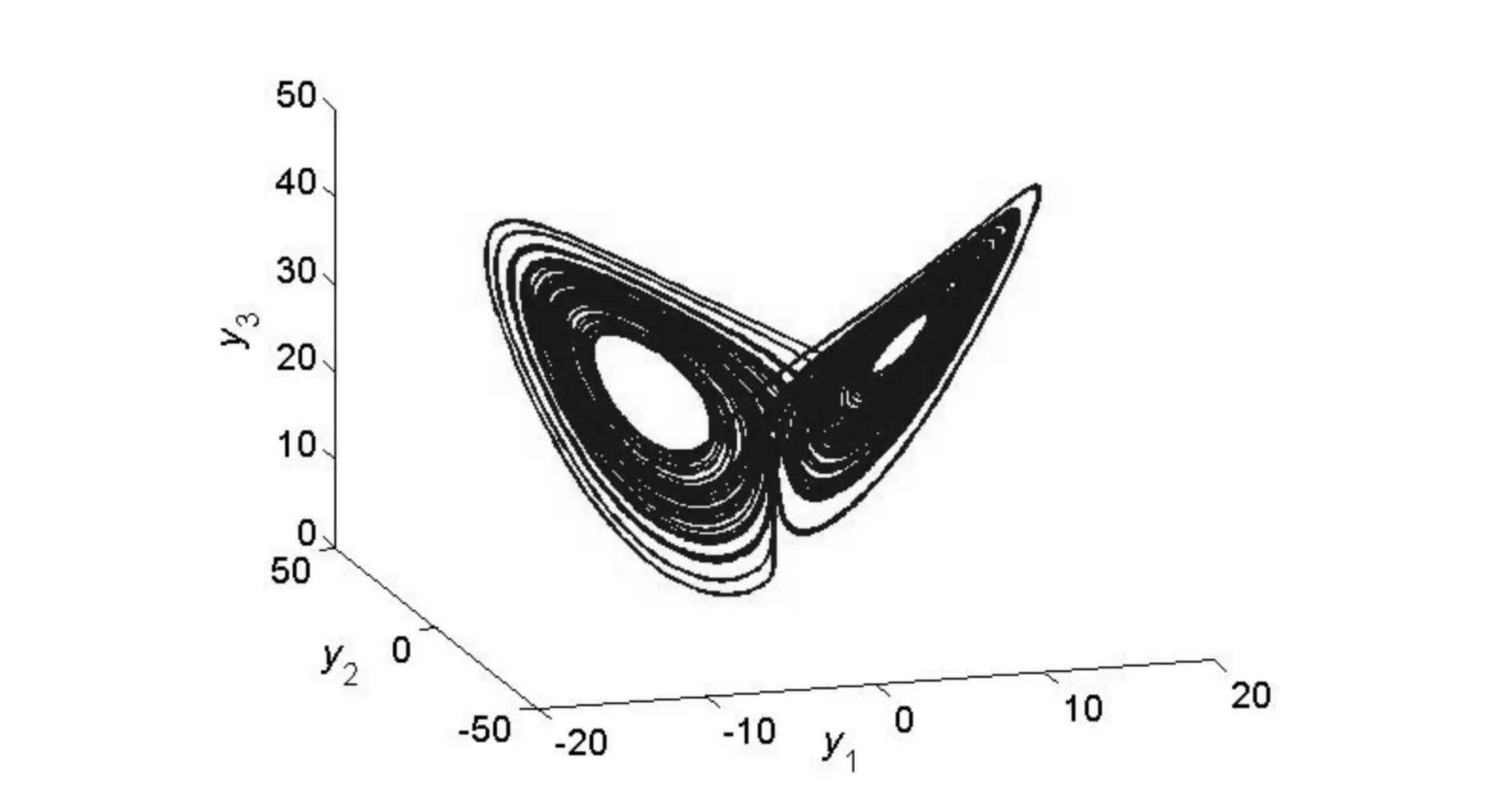
图4 线性关系下的响应系统的相图Fig.4 Phase diagram of the response system with linear relations

图5 线性关系下的驱动系统和响应系统的误差图Fig.5 Synchronization between the drive system and the response system with linear relations

图6 驱动网络和响应网络对应第一个变量之间的关系：y1=x1Fig.6 Relations between the first sub-variables in the drive system and the response system：y1=x1

3 非线性关系下的Lorenz与Chen系统的广义外同步

再讨论驱动系统和响应系统之间是非线性关系的情况.

数值仿真中，各参数变量如上所取.图7给出了驱动系统和响应系统满足非线性关系时的相图，可以看出，这两个系统之间存在着某种关系.在图8中，分别给出了驱动系统和响应系统的第1个变量和第3个变量的关系图.图9描述了在非线性关系下驱动网络和受控的响应网络之间的误差图.

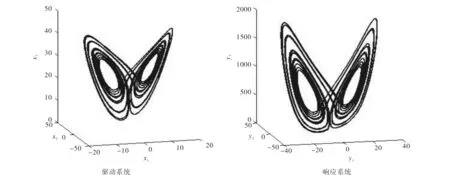
图7 满足非线性关系时，达到广义外同步的驱动系统和响应系统的相图Fig.7 The phase diagram of the drive system and the response system for achieving generalized outer synchronization with nonlinear relations

图8 驱动网络和响应网络对应变量之间的非线性关系，Fig.8 Nonlinear relationships between the sub-variables in drive system and the response

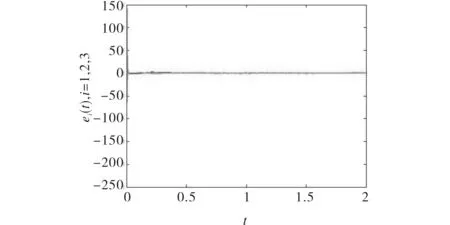
图9 在关系下的驱动系统和响应系统的误差图Fig.9 Synchronization diagram between the drive system and the response system with nonlinear relations

4 结语

在实际系统中，两个混沌系统之间一般满足线性或者非线性关系，本文针对这两种情况，讨论了在参数未知的情况下，两个动力学不同的混沌系统的广义外同步，并通过Barbalat′s引理给出了响应系统和驱动系统达到广义外同步时的自适应控制器和参数自适应律，通过对Lorenz系统和Chen系统进行数值仿真，验证了上述理论的正确性和有效性.

参 考 文 献

[1] Pecora L M, Carroll T L. Synchronization in chaotic systems [J].Phys Rev Lett,1990,64:821.

[2] Pecora L M, Carroll T L. Synchronizing chaotic circuits [J]. IEEE Trans Circuits Syst,1991,38(4):453-456.

[3] 胡 岗，萧井华，郑志刚.混沌控制[M].上海:上海科技教育出版社,2000:78.

[4] 陶朝海,陆君安,吕金虎. 统一混沌系统的反馈同步[J].物理学报,2002,51(7) :1497-1501.

[5] 宁 娣,陆君安.一个临界系统与Lorenz系统和Chen系统的异结构同步[J].Acta Physica Sinica, 2005,54(10):4590-4596.

[6] Yang S S, Duan C K. Generalized synchronization in chaotic systems[J]. Chaos Solitons Fract, 1998,10: 1703-1707.

[7] 王兴元,孟 娟.自治混沌系统的线性和非线性广义同步[J]. 物理学报, 2008,57(2):726-730.

[8] Ning D, Wu X Q, Lu J A, et al. Generalized outer synchronization between complex networks with unknown parameters [J]. Abstract and Applied Analysis, 2013, 13: 802859.

[9] 宁 娣.参数未知混沌系统的异结构广义同步[J].中南民族大学学报：自然科学版，2013，32(4)：115-118.

[10] Lorenz E N. Deterministic non-periodic flow[J]. J Atmos Sci, 1963, 20:130-141.

[11] Chen G R, Ueta T. Yet another chaotic attractor[J]. Int J Bifurcat Chaos, 1999,9(7):1465-1466.