武汉市高校间公交线路设计及其排班方案的研究

叶小青，亓晓同，马俊明，刘 琴，黄 强

(1 中南民族大学 数学与统计学学院，武汉 430074；2 中南民族大学 计算机科学学院，武汉 430074)

截至2013年1月，武汉市约有118万名在校大学生，是全世界在校大学生数量最多的城市之一，2013年1月，武汉市人大代表提出在高校之间开通公交线路，得到了市长唐良智的共鸣[1].此提议一方面有助于为高校学生之间的合作与交流提供便利，另一方面有利于推动武汉市优质教学资源的共享.

公共交通是城市的重要组成部分，高校之间的公交线路是一种特殊的公共交通.如何设计公交线路并确定合理的排班方案是公交线路运营的基础[2].由于城市交通线路复杂且具有较大的实用价值，近年来有许多学者对公交线路设计及其排班方案问题进行了研究，利用优化模型、图论模型、综合评价模型对公交线路进行设计与选择[3-5]，根据遗传算法、并行遗传算法求解了线路排班方案的粗粒度问题[2,6,7]，建立非线性随机规划模型模拟实际调度运行中遇到的随机因素，避免了传统排班模型的弊端[8]，提出以最小化乘客等待时间为目标的动态调度模型，并采用遗传算法对模型进行了求解与验证[9]，在遗传—模拟退火算法的基础上，针对其在编码操作、选择操作和模拟退火的降温操作中存在的不足进行了几点改进，结合公交车辆调度自身的特点，兼顾公交公司与乘客的双方利益建立公交车辆行车计划模型，并结合实例，应用改进的遗传—模拟退火算法对模型进行了优化求解，验证了改进的遗传—模拟退火算法的有效性和优异性[10].

现有研究大都考虑的是常规线路的排班方案，然而高校间公交线路排班方案与常规线路相比具有明显的差异性，比如对于高校学生而言，节假日是出行高峰期，而常规的线路中每天的上下班都是高峰期，而且高校间公交线路的发车间隔应明显大于常规线路.从公平性和效率性的角度出发，司机之间的工作时长和工作量应尽量相等，且公交线路应该充分满足客流需求.基于此，本文根据调查结果，以武汉市洪山区10所高校为研究对象，首先基于旅行商问题设计一条贯穿10所高校的公交线路，然后从公平性角度，并结合基本假设确定班次和所需要的司机人数，进一步从充分满足客流需要的效率性角度建立多目标优化模型确定最优排班方案.

1 基于旅行商问题公交线路的设计

根据我们项目组的调查与统计，武汉市高校学生出行主要集中在洪山区一带，包括武汉大学、华中科技大学、武汉理工大学、华中师范大学、中南财经政法大学、中国地质大学(武汉)、华中农业大学、中南民族大学、武汉纺织大学、武汉体育学院.一条好的公交线路应该贯穿这10所高校且经过的路程最短，属于典型的旅行商(TSP)问题.旅行商问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本[11].本文将建立旅行商问题的数学规划模型设计公交线路.

1.1 基于旅行商问题公交线路数学规划模型的建立

用dij表示学校i与学校j之间的距离.xij=1或0(1表示走过学校i到学校j的路，0表示没有选择走这条路)i,j=1,2,…，10，则有如下规划模型[12]：

模型(1)中目标函数表示线路总长度最短，前2个约束条件分别表示每个学校只有1条线路进入和1条线路离开，第3个约束条件表示除起始站点和终止站点外，各条线路均不构成圈.

1.2 距离的修正及公交线路的确定

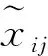
其中r>0是衰减指数，mij表示单位时间(统计周期为月)内学校i前往学校j的平均人数，Ni表示单位时间内学校i出行的学生人数.

对距离进行修正的原则是缩小互访频次较高的高校间的距离，但缩小应该是“适当的”，令r=0∶0.1∶1，对r在不同取值情况下进行聚类，结果显示当r=0.2时聚类效果最好，因此取r=0.2.

利用Lingo对模型(1)进行求解，得到最佳路线为：华中农业大学(3，起点)—武汉理工大学(2)—武汉大学(0)—华中师范大学(9)—武汉体育学院(8)—中国地质大学(4)—华中科技大学(1)—中南民族大学(6)—武汉纺织大学(7)—中南财经政法大学(5)—华中农业大学(3，终点).公交路线如图1所示.

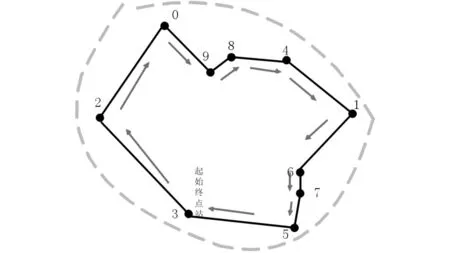
图1 武汉市洪山区10所高校间公交线路图Fig.1 The bus route map of ten universitiesin Hongshan District of Wuhan

由图1所示，该线路构成一个闭环，修正后的距离之和为24.82km，实际总长30.6km，该公交线路将距离较近的学校(如华中科技大学和中国地质大学(武汉)；中南民族大学、武汉纺织大学和中南财经政法大学)设置为相邻的站点，同时将华中农业大学设置为起点和终点，是较为合理的，因为南湖大道空旷且仅有一路公交(570路)，华中农业大学学生众多，将其设置为起点和终点不会对现有公交系统产生较大的影响.

同时，由于该线路是一条环形线路，因此可以从正向和反向同时开设公交，以满足不同方向学生的需求.

2 线路司机人数的确定

以上述公交线路为研究蓝本，考虑该线路的排班方案.排班方案的确定主要从司机角度，在线路已经设计好的基础之上，根据线路的运行时间、学生在工作日和出行日的出行规律以及司机的工作时间来确定司机人数.根据文献[13]的结论，做出如下模型假设：

①线路每天的开收班时间：6:30-21:30，共计900min.

②工作日(主要是周一到周五)出行的学生相对较少，发车间隔服从(20,30)(单位：分钟，下同)上的均匀分布；节假日出行的学生相对较多，发车间隔服从(10,20)上的均匀分布.

③完成一次线路运行的时间：工作日为60～80 min/班，节假日为80～100 min/班.

④司机每天上班不超过8h.

⑤司机连续开车不得超过4h.

⑥每名司机每月至少完成60班次.

用x1表示工作日排班间隔，根据假设①，x1:U(20,30)，工作日每天开班次数为：

(2)

其中[x]表示不小于x的最小整数.

用x2表示节假日排班间隔，根据假设③，x2:U(10,20)，节假日每天开班次数：

(3)

不失一般性，设每个月有20个工作日和10个节假日，则每月班次总数：

(4)

由于xi(i=1,2)为随机变量，考虑M的理论最大和最小值没有实际意义，因此考虑班次总数的期望值.

E(x1)=25，E(x2)=15，工作日平均每天开班36次，节假日平均每天开班60次，月均班次总数1320次.

为了确定司机人数，注意到极端情况发生在节假日，假设每次均花费100min才完成一次线路运行，则此时节假日工作时长为6000min，而根据假设④，每名司机每天最多工作480min，因此至少需要司机12.5名.同时考虑到请假等不确定因素，认为为该线路安排15名公交司机是合理的.

3 排班方案模型的建立

好的排班方案既要具有公平性，又要有效率性.公平性即各个司机之间的工作班次和工作时长应尽量均衡，效率性即排班方案应该满足客流需求，因此可建立多目标优化模型.

3.1 目标函数的建立

用xijk表示第i天第j班次第k号司机是否开车，引入0-1变量，即：

其中i=1,2,…，30，j=1,2,…,m，k=1,2,…,15,工作日时m=36，节假日对应m=60，司机总人数n=15.

用cijk表示第i天第j班次第k号司机此班次所用时间，当xijk=0时，cijk=0；当xijk=1时，cijk服从如下的均匀分布：

(5)

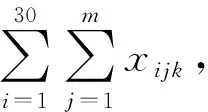
(6)

(7)

3.2 约束条件的确定

根据假设④,⑤,⑥，可以确定如下约束：

(1)司机每天上班时间不超过8h(480min)，即：

(8)

(2)由于每班次至少60 min，最多100 min，所以连续开车不超过4h等价于不能连续开车4班次, 即：

(9)

(3)司机每月至少完成60个班次，即：

(10)

联立(7)～(10)式，得到公交车排班方案的多目标优化模型：

(11)

4 排班方案模型的求解

模型(11)属于多目标优化模型，多目标优化模型没有全局意义上的最优解，线性加权法和分层排序法是多目标优化模型常用的求解方法.线性加权法主要按各分函数的重要程度，对应地选择一组加权系数，其所有加权系数和为1，各分函数与加权系数乘积的线性组合构成一个评价函数，求新的评价函数最优解.分层排序法主要思想是基于各个目标函数并按某种意义分清主次，按重要程度逐一排队，然后依次对分目标函数求各自的最优解.由于模型(11)中S1和S2分别代表司机的月工作班次方差和月工作时间方差，而且后者以分钟为单位，最终结果将会很大，这样必定会导致两者的量纲差异性较大，不适合线性加权法；同时，S1和S2在本模型中的重要程度相同，没有主次之分，因此也不适合分层排序法.考虑到本模型的复杂性主要在于约束条件，因此采用如下算法步骤对模型进行求解.

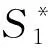
Step2：不考虑目标函数的取值，对约束条件进行随机模拟，得到一种符合条件的排班方案；

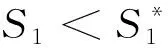
该求解思想的算法流程图如图2所示.

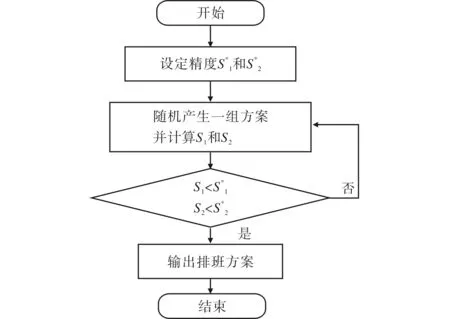
图2 模型求解的算法流程图Fig.2 The algorithm flow chart of model solution

4.1 阈值的确定

模型结果的好坏很大程度上取决于阈值的确定.阈值的确定应该充分体现排班方案所应满足的公平性(排班方案的效率性体现在约束条件中)，确定的阈值过大，则模型的精确度会过低；阈值过小，则模型的求解代价会过大.借助概率论与数理统计中次序统计量和分位数的概念，本文采用如下步骤确定阈值：

Step1：随机模拟约束条件进行100次，产生100组目标函数值，每组目标函数值均包括班次方差和工作时间方差；

Step2：将目标函数值按照从小到大的顺序进行排列，用S1(i)和S2(i)分别表示排列后的第i个班次方差和工作时间方差；

该阈值确定方法表明仅接受随机模拟中80分位及以上的目标函数取值.利用MATLAB进行模拟，得到阈值

(12)

4.2 排班方案的模拟结果

在图2所示的流程图的基础上，本文采用MATLAB语言进行编程求解，其程序伪代码如下：

Function

put(flag); %输入当月天数信息，1表示节假日，0表示非节假日

size(flag); %当月天数

for k=1:size(flag) %循环输入调整当月所有天数的排班信息

all(zeros) %所有排班初始信息置零

while T<=900 %当天累计运行时间

Bus(k,Num,4) %初始化当天所有班次四项信息

end

for i=1:Num %循环更新所有当天班次四项信息

for j=1:n %循环更新第n个司机的信息

if Dr(k,j,:)=1 %如果司机所有的要求都满足

end

if Dr(k,j,:)=0 %如果该司机不是所有的要求都满足

Dr(k,j,:)=0—>Dr(k,j,:) %更新该司机的信息使其满足要求

end

end

end

end

printf( ) %输出结果

基于上述代码可得到该公交线路的排班方案及司机工作量统计表.公交车的发车时间一旦确定，则各个站点的具体到站时间取决于相邻两站点间的距离和该路段交通情况，具有一定的随机性.尽管各个站点在工作日与节假日排班方案的结果均由计算机随机模拟求得，但均符合模型假设②和③：即学生的平均等车时间分别不超过25 min(工作日)和15 min(节假日)，每班次的时长不超过80 min(工作日)和100 min(节假日).需要出行的学生可以根据发车时间合理地安排自己何时去车站候车.

由于输出结果庞大，表1～2仅给出华中农业大学(起点站)工作日和节假日前10个班次的具体排班方案.

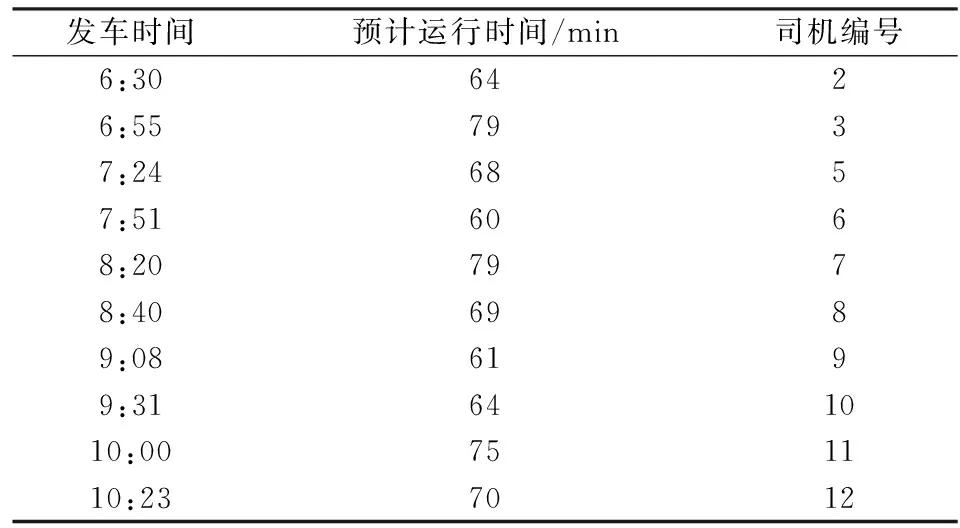
表1 华中农业大学(起点)工作日排班方案信息表(前10班次)Tab.1 The information table of scheduling program on weekdays in the starting point of Huazhong Agricultural University(top 10 shifts)

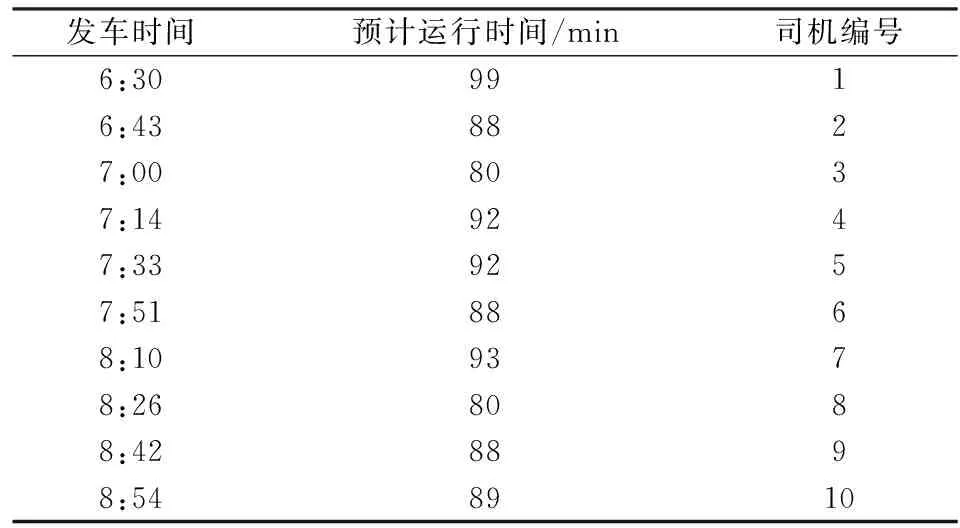
表2 华中农业大学(起点)节假日排班方案信息表(前10班次)Tab.2 The information table of scheduling program on holidays inthe starting point of Huazhong Agricultural University(top 10 shifts)

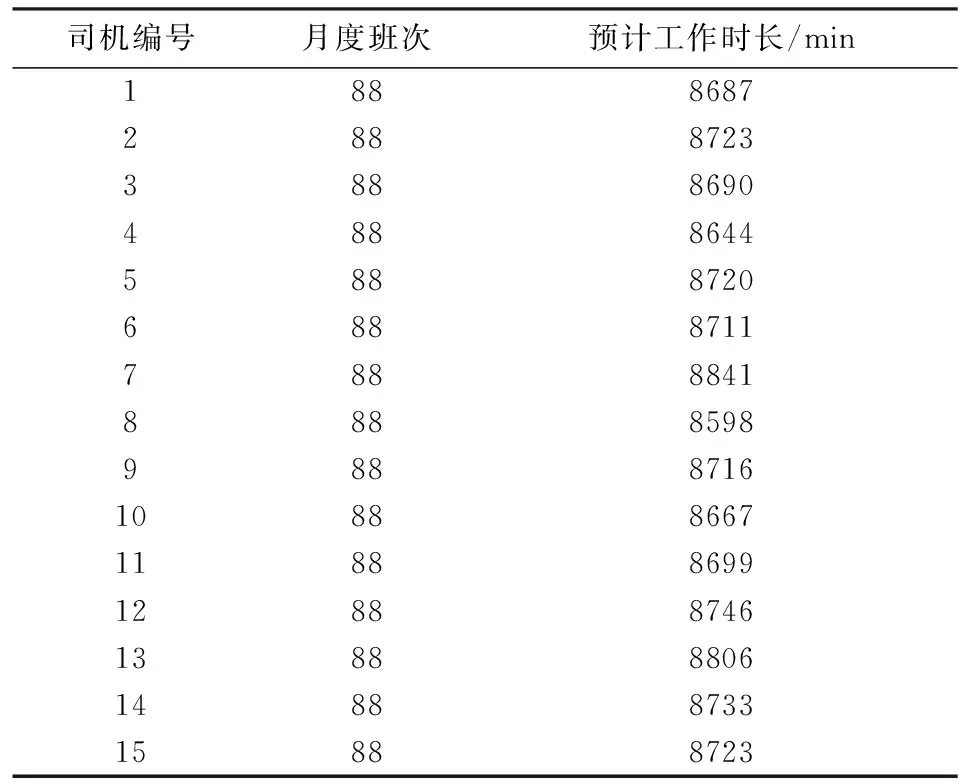
表3 15名司机月度班次和工作时长统计表Tab.3 The statistics of monthly shift and working hours of 15 drivers

5 结语

本文首先根据互访人数对高校间的距离进行了修正，建立基于旅行商问题(TSP)的数学规划模型，设计出一条贯穿武汉市洪山区10所高校间的公交线路.其次从效率性入手，通过期望分析确定了该公交线路上合适的司机人数；再从公平性角度，以司机的工作量和工作时长方差最小入手建立了多目标优化模型，通过设定阈值，结合计算机模拟确定了公交司机在工作日和节假日的排班方案，结果表明该方案下公交司机的工作量和工作时长非常均衡，具有一定的推广意义.

参 考 文 献

[1] 大楚网. 武汉今年送大学生“三大福利”，试点高校间通公交[EB/OL]. [2013-6-18].http://hb.qq.com/a/20130108/000402.htm.

[2] 衷 明. 基于并行遗传算法的智能公交排班研究[J]. 计算机时代，2011(12)：18-20.

[3] 周文峰，李珍萍，刘洪伟，等. 最优公交线路选择问题的数学模型及算法[J].运筹与管理，2008，17(5)：80-84.

[4] 马良河，刘信斌，廖大庆. 城市公交线路网络图的最短路与乘车路线问题[J].数学的实践与认知，2004，34(6)：38-44.

[5] 钱 萌，彭张节，陈树林，等. 基于综合评价指数的城市公交线路选择优化模型[J].吉林大学学报：信息科学版，2008，26(2)：180-185.

[6] 李越鹏. 基于遗传算法的公交车辆智能排班研究[J]. 交通运输系统工程与信息，2003，3(1)：41-44.

[7] 王 宁，宫生文. 基于遗传算法的公交智能排班系统的设计与实现[J]. 计算机时代，2008(9)：38-40.

[8] 杨 磊，刘卫朋，周 磊. 基于改进的随机公交调度问题的数学模型[J]. 河北工业大学学报，2010，39(1)：74-78.

[9] 姚宝珍. 城市公交枢纽布局与运营调度方法研究[D]. 北京：北京交通大学，2011.

[10] 黄宏用. 改进的遗传—模拟退火算法在公交排班中的应用[D]. 兰州：兰州理工大学，2011.

[11] 刁在筠. 运筹学[M]. 3版. 北京：高等教育出版社，2005.

[12] 司守奎. 数学建模算法与应用[M].北京：国防工业出版社,2011.

[13] 数据堂. 公交司机排班方案[EB/OL]. [2013-6-20]. http://www.datatang.com/data/39666.