基于模糊集的时序关联规则的度量准则
2014-08-06宋中山
宋中山,杨 敏,周 易
(中南民族大学 计算机科学学院,武汉 430074)
Agrawal和Srikant首次提出了序列模式挖掘问题[1],L A.Zadeh提出了模糊集的重要概念[2],把经典集合推广到模糊集.现存的模糊序列模式挖掘算法,大多是针对传统序列模式挖掘算法作适当修改而得到的.Tzung-Pei Hong等人基于AprioriAll算法,提出了模糊序列模式挖掘算法Fuzzy-Apriori算法[3],该算法不可避免地具有AprioriAll算法多次扫描数据库,不易发现长序列模式的缺点.模糊序列模式挖掘的一般化架构,需对数据库中的数量属性进行模糊化处理.在现实的购物序列数据库中,项的数量值、交易之间的时间间隔等都是数量属性.近年来,针对模糊序列模式挖掘,人们提出了很多新的方法[4-6],都取得了较好的效果,扩展了模糊序列模式挖掘的应用范围.
现有时序关联规则算法,一般在处理高密度海量数据时会生成规模庞大的频繁项候选集,整个过程要消耗大量的时间,并需要重复多次扫描数据库,执行效率低.本文针对时序关联规则在解决商品项分类时所出现的不精确和不确定分层情况,对层次型关联规则模式进行模糊扩展,用以克服不同隶属度项的语义差异的不足,给出了基于模糊集的时序关联规则的度量准则,通过实验验证了该方法的有效性.
1 时序关联规则度量
关联规则挖掘最早由Agrawal等人提出,是为了发现顾客交易数据库中项集间的关联信息.由于关联规则挖掘在数据挖掘中的广泛应用,已经产生了大量的关联规则挖掘算法.为了揭示关联规则随时间变化的特性,在处理时序关联规则中,运用支持度向量SV和置信度向量CV来分析关联规则的时序特性[7].
假设在时间t内生成事务数据集D,那么可以将t分成n个不相交的时间序列,记为t={t1,t2,…,tn},由此可以得到n个数据子集,记为D={D1,D2,…,Dn}.其中,任意数据子集Di是在时间段ti(i∈1,2,…,n})中生成的.
设项集I={i1,i2,…,im},若X⊂I,Y⊂I,且X∩Y=Φ,那么可以将X⟹Y这样的蕴涵式称为关联规则.它的支持度为s和置信度为c,那么,公式s=PD(X∪Y)给出了D中既含X又含Y的概率;公式c=PD(Y|X)给出了D中既出现X又出现Y事务集的概率.
定义1 时序关联规则X⟹Y的支持度向量SV定义为:
SV=(s(X∪Y)1,s(X∪Y)2,…,s(X∪Y)n),
s.t.s(X∪Y)i=f(X∪Y)i/|Di|(i∈(1,2,…,n).
(1)
其中,f(X∪Y)i为项集X∪Y在数据子集Di(i∈{1,2,…,n})中出现的频数;|Di|为Di中的事务数.那么,s(X∪Y)i反映了项集X∪Y在Di中的支持度.X⟹的支持度s可表示为:
(2)
其中,f(X∪Y)为项集X∪Y在D中出现的频数;s(X∪Y)为项集X∪Y在D中的支持度.M是D中的事务数.
定义2 时序关联规则X⟹Y(或者项集X∪Y)的置信度向量CV定义为:
CV=(c(X∪Y)1,c(X∪Y)2,…,c(X∪Y)n),
(3)
其中,s(X∪Y)i为项集(X∪Y)的SV中的第i个元素;sXi为项集X的SV中的第i个元素.
上述定义中,c(X∪Y)i反映了项集(X∪Y)在Di中的支持度量.X⟹Y的置信度c可表示为:
c=s(X∪Y)/SX.
(4)
综上所述,可以得到新的时序关联规则的完整定义.
定义3 时序关联规则的完整定义包括支持度s、置信度c、支持度向量SV和置信度向量CV等4个参数,完整定义如下:
X⟹Y(SV,CV,s,c),
(5)
其中,SV、s、CV和c分别由公式(1)、(2)、(3)和(4)给出.
定义4 时序关联规则X⟹Y的频数向量可以定义为:
FV=(f(X∪Y)1,f(X∪Y)2,…,f(X∪Y)n),
(6)
其中,f(X∪Y)i为项集(X∪Y)在数据子集Di(i∈{1,2,…,n})中出现的频数.
那么,时序关联规则挖掘的过程如下:
(1) 计算频数向量FV和频繁项集L;
(2) 由L生成时序规则,FV生成SV、CV.
2 模糊时序关联规则
模糊集理论最根本的特征是承认事物变化的过渡状态,若模糊集A是论域X上满足某些性质的一类对象,其中每个对象都有一个隶属于A的程度称为隶属度,隶属函数μA(x)(x∈X)将每个对象x映射到区间[0, 1].人们把L. Zadeh的模糊理论用于语义研究[8],认识到模糊性也存在于人类自然语言中,是它的一种客观属性,而它描述的是词语所指范围的不确定性.由于人们在认知过程中对有中间状态的事物或现象具有认识上的任意性或主观性,就不可避免地会产生模糊语义.
模糊语义指语义的模糊性,针对层次型关联规则在构造层次分类树的过程中时所出现的不精确和不确定分层情况,对其进行模糊扩展:即对于X⟹Y这样的蕴涵式,若X和Y是模糊集合,则对应的关联规则就为模糊关联规则(Fuzzy Association Rule).
模糊层次分类结构是指具有隶属度模糊的概念层次树[9].通过建立带语义差异的模糊层次分类结构,就能够计算项间距离、项集间距离,逐步得到最终的关联规则间距离度量的方法.
定义5 设有带语义差异的模糊层次分类结构T=
(7)
其中,w′(e)是有向边e的语义差异权值,x是y的祖先,lmin(x,y)是x和y间所有向路径中语义差异权值最小的.
本文使用平均距离来计算项集间距离,这样就有:
定义6 设有基数为m的项集X={x1,x2,…,xm}和基数为n的项集Y={y1,y2,…,yn},则X和Y之间的项集距离定义为:
(8)
在对关联规则距离进行度量的过程中,分析对其起决定作用的2个因子:结构差异和规则度量差异,进而由规则的结构距离、规则度量距离来定义规则距离.
定义7 在带语义差异的模糊层次分类结构T=
Distrule,stru(r1,r2)=λ1×Distset(X1,X2)+λ2×
Distset(Y1,Y2)+λ3×Distset(X1∪Y1,X2∪Y2).
(9)
若Conf(r1),Sup(r1),Conf(r2),Sup(r2)分别为规则r1,r2的支持度和置信度,λ4,λ5≥0,则r1,r2间的规则度量距离可表示为:
Distrule,meas(r1,r2)=λ4×|Sup(r1)-Sup(r2)|+λ5×
|Conf(r1)-Conf(r2)|.
(10)
这样,设有权重w1,w2,则r1和r2间的规则距离可表示为:
Distrule(r1,r2)=
(11)
综上所述,λ1,λ2,λ3是结构距离Distrule,stru(r1,r2)中前项、后项和两者并集的差异的权重;λ4,λ5是度量距离Distrule,measu(r1,r2)中支持度和信任度的差异的权重;w1,w2是规则距离Distrule(r1,r2)中用户定义的结构差异和度量差异的值.
3 实验设计
本文使用George Karypis等人研发的gCLUTO聚类工具包,进行关联规则的聚类和可视化,本文选择重复对分(Repeated Bisections)的聚类算法.
通过对T10I4D100K数据集进行测试来验证关联规则距离度量方法的有效性,其中,T10I4D100K来自IBM Almaden Quest 研究组的频繁项集,处于稀疏型数据和密集型数据之间.对于数据集中的1000个商品项目,共有100000条交易数据,给它设定不同的支持度和置信度,用OFP-Growth算法对时序关联规则进行挖掘[10].
由于经过时序关联规则挖掘后得到的规则数量较大,而且其距离度量计算过程中的消耗较大,不能进行实时处理.本文有必要将整个实验分为2部分进行.
如表1所示,在给定的支持度和置信度下,本文得到关联规则集RS1和RS2,其中RS1用于时序关联规则距离度量的实验;RS2用于聚类及规则间相似性的可视化实验.

表1 OFP-Growth算法得到关联规则结果
本文将T10I4D100K数据集的模糊层次分类结构记为T,根据其定义,就可以进行如下描述.
(1)T共有1个有向无环图,可将其分为4层,最上面的是树根节点ROOT,平均扇出为10;
(2) 建立模糊层次分类结构有向边时,可以随机生成其模糊隶属度,使l/3的模糊隶属度随机均匀分布在区间[0.5, l]中,2/3的模糊隶属度为1;
(3) 相邻不同层次a,a+1,1≤a≤3的层次语义差异计算函数设置ld(a,a+1)=(3-a+1)/10;
(4) 不相邻层次a,a+n,n>1的层次语义差异计算函数设置为:
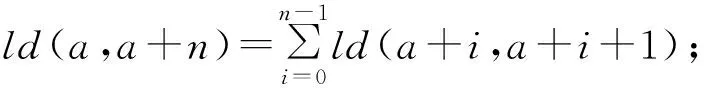
(5)权重参数设置为:
λ1=1,λ2=1,λ3=0,w1=1,w2=0.
本文的实验平台为PC,2GB内存,Intel Core i3 CPU,Windows7操作系统,用VC 6.0来编程实现关联规则距离的度量.
在进行关联规则距离度量的过程中,本文使用RS1规则集,并以每次递增600条关联规则的方式来测试计算时的速度.当规则数量为n时,关联规则间距离的度量需要计算n×(n+1)/2次规则间的距离.
因为在关联规则距离度量的过程中,构建带语义差异的模糊层次分类结构T所耗费的时间与整体性能相比很小,可以忽略不计.
将本文由公式(8)给出的项集度量方法与文献[11]、文献[12]的方法进行比较.它们随关联规则数量的增加所消耗的时间对比如图1所示.
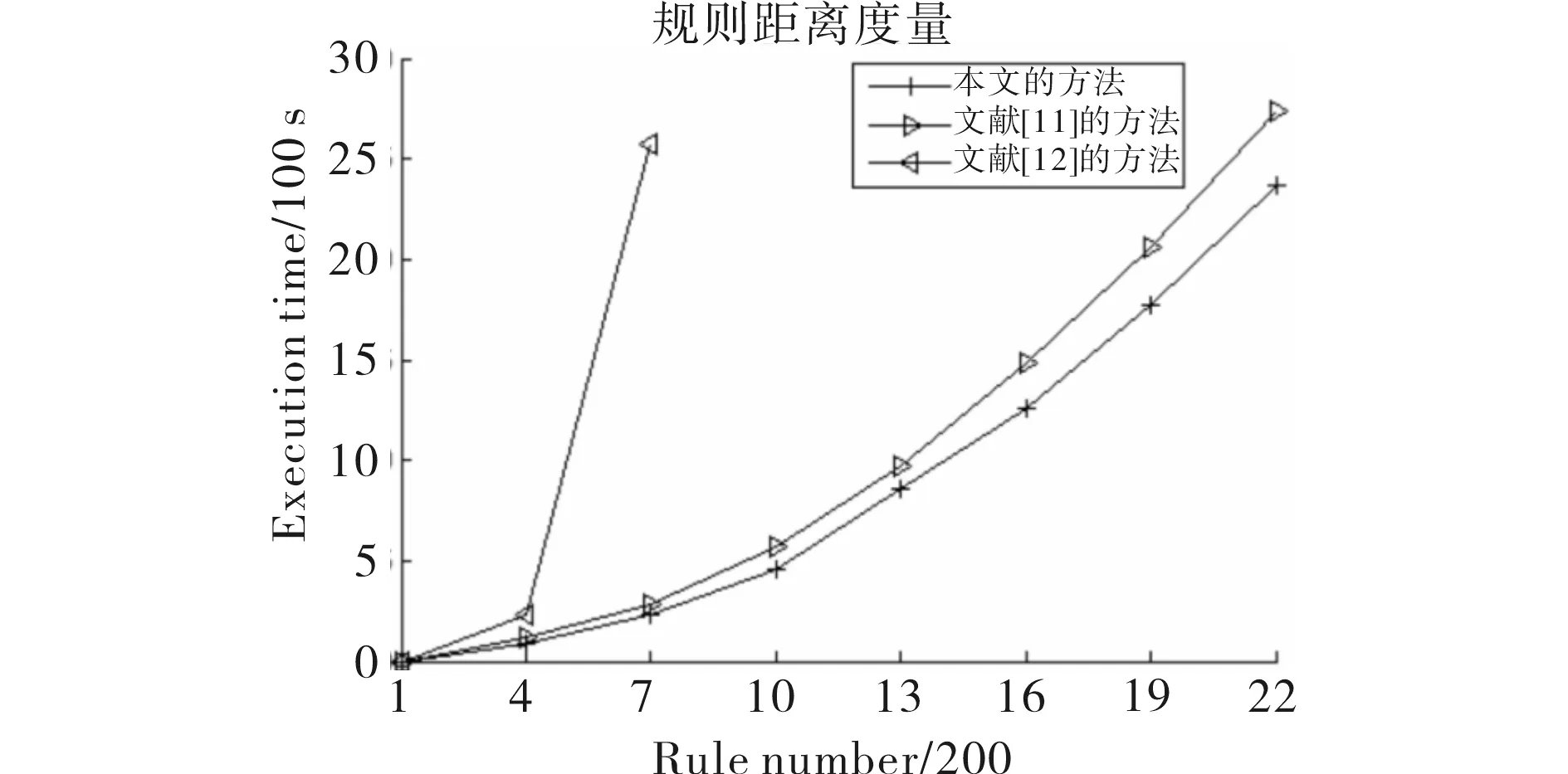
图1 关联规则距离度量耗时Fig.1 Execution time of measuring distance among association rules
本文使用gCLUTO聚类工具包来聚类分析关联规则结果,并对结果进行可视化展示[10].本文使用规则集RS2,设置重复对分(Repeated Bisections)类别为8类.取得了较好的效果,如图2、图3所示.
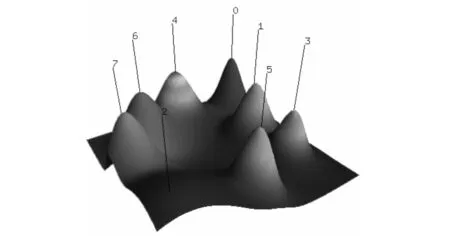
图2 关联规则聚类的山丘视图Fig.2 Mountain view of association rules clustered
图2中可视化山丘将8个类群显示为8个山丘,并标记了相应的类号.每个山丘的形状为高斯曲线.这种形状用来作为每个类内数据分布的粗略估计.山丘的高度与类内相似性成比例,体积与类群包含的对象数量成比例.合成的高斯曲线相加在一起形成可视化山丘的地形.山丘的颜色与类内标准差成比例.红色代表低标准差,蓝色代表高标准差.只有峰顶的颜色是有意义的.在其他所用区域,颜色混合以产生平滑过渡.

图3 关联规则聚类的树形视图Fig.3 Tree view of association rules clustered
图3中的可视化矩阵中,颜色代表原始数据矩阵中的数值.gCLUTO用白色代表接近零值,逐渐加深的红色代表较大的数值,逐渐加深的绿色代表负值.矩阵的行重新排列,使得同一类的行列在一起.黑色的水平线隔开各个类.左面和上面关联规则聚类后得到的树形结构,说明了规则间的组织方式;右下角部分给出了可视化的关联规则的相似性.右下角部分的每一点都说明了横纵坐标对应的两个规则间的相似性,红颜色越深,表示规则间的相似性越高.
观察图3可以发现,对角线上红颜色很深,表示类间的关联规则间的相似性较低,类中的关联规则间的相似性比较高.
4 结语
本文针引入的层次型关联规则的模糊扩展,即基于隶属度模糊的层次分类结构,克服了原有分类结构仅仅考虑不同层次之间的语义差异,而没有进一步考虑具有不同隶属度项的语义差异的不足.使用本文定义的项间距离、项集间距离和关联规则间距离的度量,构建模糊层次分类结构,实验结果表明,该方法是有效的,并具有良好的性能.将时序关联规则结果进行聚类分析,得到规则和规则之间相似性,并进行可视化展示.在实际问题中,模糊集的时序关联规则将其应用到带语义模糊的商品分类中,为企业合理有效的管理提供依据,并可根据发现的知识和规律广泛地应用到描述客观现实情况,重现及识别动态系统,及时调整企业经营策略.
参 考 文 献
[1] Agrawal R, Srikant R. Mining sequential patterns[C]// ICDE.Proc of the International Conference on Data Engineering (ICDE). Taibei: IEEE, 1995: 3-14.
[2] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353.
[3] Hong T P, Kuo C S, and Wang S L. A fuzzy AprioriTid mining algorithm with reduced computational time[J]. Applied Soft Computing, 2004, 5(1): 1-10.
[4] Zabihi F, Pedram M M, Ramezan M, et al. Fuzzy sequential pattern mining with sliding window constraint[C]//ICETC. 2010 2nd International Conference on Education Technology and Computer (ICETC). Shanghai: IEEE, 2010, 5: 396-400.
[5] Chang C I, Chueh H E, Luo Y C. An integrated sequential patterns mining with fuzzy time-intervals[C]//ICSAI. 2012 International Conference on Systems and Informatics (ICSAI). Yantai: IEEE, 2012: 2294-2298.
[6] Ouyang W. Discovery of direct and indirect fuzzy sequential patterns with multiple minimum supports in transaction databases[C]//FSKD. 2012 9th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD). Chengdu: IEEE, 2012: 302-306.
[7] 荣 冈,刘进锋,顾海杰.数据库中动态关联规则的挖掘[J]. 控制理论与应用, 2007, 24(1): 127-131.
[8] Zadeh L A. Fuzzy sets as a basis for a theory of possibility [J]. Fuzzy Sets and Systems, 1999, 100(1): 9-34.
[9] Chen G, Qiang W. Fuzzy association rules and the extended mining algorithms[J]. Information Sciences, 2002, 147(1-4): 201-228.
[10] 宋中山,周 腾,周晶平.一种改进的蚁群聚类算法在客户细分中的应用[J].中南民族大学学报:自然科学版,2013,32(3):77-81.
[11] 阮备军,朱扬勇.基于商品分类信息的关联规则聚类[J]. 计算机研究与发展, 2004, 41(2): 352-360.
[12] Gupta G, Strehl A, Ghosh J. Distance based clustering of association rules[C]//ANNIE. Proc of Intelligent Engineering Systems Through Artificial Neural Networks (ANNIE 1999). St. Louis: ASME Press, 1999: 759-764.
