基于图论的DNA微阵列数据聚类算法

宋 佳，许 力，孙 洪

(1. 浙江大学电气工程学院，杭州 31002 7；2. 苏州市职业大学电子信息工程系，江苏 苏州 21 5104)

基于图论的DNA微阵列数据聚类算法

宋 佳1,2，许 力1，孙 洪2

(1. 浙江大学电气工程学院，杭州 31002 7；2. 苏州市职业大学电子信息工程系，江苏 苏州 21 5104)

传统的聚类算法用于DNA微阵列数据分析时，多数只能生成一种聚类结果，无法识别出与多组不同基因表达模式相类似的基因。针对该问题，提出一种基于图论的聚类算法，采用一个有向无权图来描述需要分析的DNA微阵列数据，分别计算该图具有最小割权值和第二小割权值的图割。测试结果表明，该算法可以有效地探测聚类结果空间并输出一组可能性较高的聚类结果，与Fuzzy-Max、Fuzzy-Alpha、Fuzzy-Clust等聚类算法相比具有更高的准确性。

微阵列；基因表达数据；聚类分析；图割；图论；最小割

1 概述

DNA微阵列技术的发展使得研究人员可以同时监测并获得各种环境下成千上万个基因的表达水平，产生了海量的基因表达谱数据[1]，从而深入地认识诸多生物过程的本质，如基因功能、发育、癌症、衰老和药理等。因此，建立能够准确处理和分析DNA微阵列数据集的方法是目前生物信息学发展的一个重要方向。聚类算法就是用于查找功能相关的基因和疾病新子群的主要方法之一。聚类算法根据目标研究对象的属性数值，采用数学方法对其进行分类和整理，将具有相似属性的事物聚为一类，使得同一类的事物尽可能相似，而不同类的事物间有较大的差别。因此，聚类算法的准确性对于准确识别功能相关的基因起着关键性的作用，是进行表达数据中数据挖掘的第一步，其效果直接影响后续的表达谱数据分析性能。

聚类算法可以分为有监督的聚类算法(或分类，classification)、无监督的聚类算法和混合聚类算法。在有监督的聚类中，聚类基于一个给定的参考方向集或类别集；在无监督聚类中，聚类分析预先不知道类别信息，没有训练集；混合聚类通常先进行无监督聚类，确定一些类，再用神经网络或支持向量机这些可以学习数据类别之间决策边界的分类器，将新基因归到不同的类内。基因表达阵列实验尚处于早期阶段，无监督聚类算法仍是最常用的。

目前，已有大量的无监督聚类算法和软件被开发出来并用于分析DNA微阵列的数据，如K-means算法、平均连锁聚类、基于最小遍历树聚类法、自组织映射等。这些聚类算法将相应条件下表达相似的基因归为一类。在实际应用中，由于噪声等原因，存在大量的基因不属于任何一个聚类，同时也存在一些基因可以在不同生物过程中与不同的基因分组一起发挥不同的作用，从而出现在多个聚类中。而上述的这些聚类算法大多只能生成一种聚类结果，无法识别出与多组不同的基因表达模式相类似的基因，难以获得在不同条件下与多组基因共调控的基因之间的关系。近年来，针对这一缺陷，研究者们提出了一些更为复杂也更加适宜于基因表达数据分析的的聚类算法[2-3]，这些算法大多基于模糊聚类(fuzzy clustering)。模糊聚类算法[4-5]的特点是并没有强制将每个基因归入到某个特定的聚类中，而是分别计算每个基因归属各个聚类的隶属度，通过隶属度值的大小来表示基因隶属某个聚类的程度高低。但是，这些模糊聚类算法也存在若干缺陷，如模糊参数值很难设置、计算复杂度高，算法也常常无法识别出所有的聚类。

图论(graph theory)是离散数学的一个分支，它以图为研究对象，研究顶点(vertex)和边(edge)组成图形的数学理论和方法。图论中的图形通常可以用来描述某些事物之间的某种特定关系，例如用顶点代表事物，用连接两顶点的边表示2个事物间具有某种关系。因为图论是一门研究较早并且已经发展成熟的学科，具有较好的数学基础，应用图论方法解决生物信息学问题也越来越引起学者的重视。基于图论的聚类算法主要包括Random Walk、CHAMELEON、AUTOCLUST等[6-7]。近年也有一些利用图的着色理论[8]、阈值剪枝[9]，以及谱图[10]等理论的聚类算法被提出。这些算法也只能生成一种聚类结果。

本文提出一种以图论为基础的聚类算法，将DNA微阵列数据集映射成加权图，分别计算图的最小割和第二最小割，并依据每个图割，将图分别分割成2个子图，在每个子图上迭代地应用这个算法，直到没有新的集群出现为止。此外，本文还设计了一种可以在多项式时间内计算出有权图的第二最小割的算法，并从理论上证明其正确性，以持续更新并输出一组可能性较高的聚类结果。

2 模型与算法

2.1 D NA微阵列数据的获取和预处理

DNA微阵列也称为基因微阵列，目前有2种模式：cDNA微阵列和Affymetrix基因芯片(或寡核苷酸阵列)，它们的原理相同，即利用4种核苷酸(A, T, C, G)之间两两配对互补的特性，使2条在序列上互补的单核苷酸链形成双链(即杂交，hybridization)。以cDNA微阵列为例，在一个表面处理过的固体支撑物(通常是尼龙或玻璃)上，cDNA以固定的模式排列。用于测试的mRNA样本被反转录成cDNA并用荧光染色标记，这些cDNA与阵列上的DNA探针进行杂交，用激光显微镜或荧光显微镜检测杂交后的芯片，获取荧光强度，最后通过图像处理和分析得到测试样本中mRNA的丰度信息。

计算机读出的微阵列数据矩阵C(N×M)表示N个基因在M个样本(或M个不同的实验条件)上的表达矩阵：

矩阵C中每一行代表一个基因，每一列代表一张芯片上基因的数据。cij为基因i在实验j中的表达值。依据基因芯片的实验原理，cij取为相对的荧光强度比值：

其中，IR为芯片上红色荧光剂(样本组基因)的强度；IG为芯片上绿色荧光剂(对照组基因)的强度，对其分别取对数可以避免以下差异：当基因高表达时，表达比在(1,+∞)，当基因低表达时，表达比在(0,1)，两者存在不对称性。基因可以看作是含有M维实数的向量，而样本可以看作是N维实数的向量。根据不同的实验，基因表达值可以采用同样的算法分别对实验条件(列)或基因表达谱(行)进行聚类。

在进行聚类时，都需要对数据之间的相似度进行评估，这个评估通常采用距离函数来实现。目前有2种距离函数广泛用于比较基因表达谱：欧几里德距离函数和皮尔森距离函数。具体函数的选择主要取决于研究者想要测量的特性。本文采用欧几里德距离来度量基因之间的相似性。给定2个向量：它们之间的欧几里德距离可以用下式来计算：

欧式距离测量空间中2个点的绝对距离，故同时考虑了矢量的方向和幅度。若直接使用原始数据进行计算，则表达谱幅度相似的基因将被认为是相似的。但生物学上更倾向于寻找表达水平不同而表达谱形状相似的基因，因此，在使用欧式距离前需对微阵列数据作归一化处理：

其中，µi和σi分别是ci的均值和方差。

2.2 图的构建

在对DNA微阵列数据归一化处理后，采用一个无向有权图G(V, E, W)来描述需要分类的微阵列数据，图的顶点V代表基因，两顶点之间的欧式距离如果小于给定的阈值T，则2个顶点由边界连接。每条边界都有一个权值，连接顶点vi和vj的边界权值可以表示为：

其中，d( vi, vj)即两数据点之间的欧式距离；K为常数。很明显距离越大，则对应的边界权值越小。为了便于分析，本文假定图G是连通的。因为即使图G不连通，也可以分别在每个连通的子图上继续之后的工作，结果仍然适用。

2.3 图的最小割和第二最小割计算

2.3.1 最小割计算

最小割问题[11-12]可分为s-t最小割和全局最小割。s-t最小割是指给定源点s和汇点t，能将s和t分别分割到2个子图中的最小割。全局最小割指所有s-t最小割中值最小的割。著名的最大割最小流定理证明最大流和s-t最小割是一对对偶问题。显然，全局最小割在计算时，需要计算(|V|(|V|-1))/2个最大流(分别对应不同的源点s和汇点t)。文献[13]提出一种算法，只需计算(|V|-1)个最大流。给定一个有权无向图G(V, E, W)，全局最小割的计算可通过以下步骤：(1)令min=∞，确定一个源点s；(2)枚举汇点t，t∈V-s；(3)计算最大流，并确定当前源汇点的最小割值，若比min小，则更新min；(4)转到步骤(2)直到枚举完毕；(5)min即所求输出min。

以上最小割计算中枚举汇点的计算时间为O(|V|)。如果采用最短增广路最大流算法来求最大流，时间复杂度是O(|V|2|E|)，则算法总复杂度为O(|V|3|E|)；而如果采用最高标号预流推进法来求最大流，时间复杂度为O(|V|2|E|0.5)，则算法总复杂度为O(|V|3|E|0.5)。文献[14]通过优化汇点t的选择顺序，改进以往的预流推进算法，最终得到一个O(|V||E|)时间的全局最小割算法，其时间复杂度和计算一个s-t最小割是一致的。

2.3.2 第二最小割计算

最小割问题可以在多项式时间内计算出，但还不能确定割值为第二小的图割是否也能在多项式时间内算出。下面证明它也能在多项式时间内计算出，并且可用于本文的聚类算法来探索所有的聚类结构所组成的空间。

定理1给定一个有权无向图G(V, E, W)，具有第二小割权值的图割可以在时间O(|E|×f(|E|,|V|))内算出，其中，f(|E|,|V|)是计算图G全局最小割的时间复杂度。

证明：通过下列步骤可以计算出具有第二小割权值的图割。(1)计算图G具有最小割权值的图割，并假定割边集为C；(2)对于边界(a, b)∈C，收缩(a, b)可以得到一个新图G'；(3)计算图G'的最小割权值的图割，并把结果放置在集合U中；(4)把边界(a, b)从C中移除，如果集合C非空则回到步骤(2)；(5)对集合U中的全部图割，计算出其中具有最小割权值的图割并输出。

下面证明此第二小割权值算法的正确性：具有第二小割权值的图割必须至少包括一条不在具有最小割权值的割集中的割边，因而算法中步骤(2)～步骤(4)的穷举搜索可以找出具有第二小割权值的图割。因为C可能包含最多|E|条边界，这种算法所需的时间为O(|E|×f(|E|,|V|))。

上述步骤(2)中的收缩(a, b)即删掉点a、b及边(a, b)，替代为新顶点n，如图1所示。其中，对图G中除a、b外的任意顶点v，其与n的边权值为：

w( v, n)=w( v, a)+w( v, b) (5)

图1 边的收缩

2.4 高连通图的判定

文献[15]提出高连通图的概念，并将其应用于无向无权图的分割。这里对其定义进行引申后，引入之前建立的无向有权图中，并将其作为图分割的终止判据。

当分割所得的子图为高连通图时，认为它可以作为一个聚类，不再继续分割。如图2所示，对图G进行分割，其中，图2(a)为第一次分割结果，得到2个子图G1，G2，因为G1为高连通子图，所以不再继续分割，图2(b)中继续对G2分割，得到2个高连通子图G3，G4，分割结束。图中的虚线表示最小割。

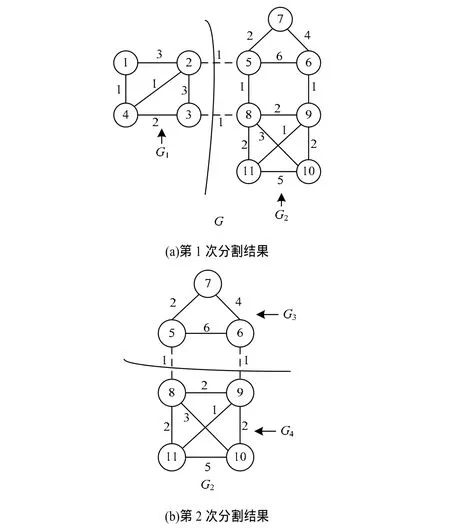
图2 图G的分割

定理2高连通图中的任意一个顶点至少与图G中一半以上的顶点相邻。

证明：对于高连通图G，如果将与其度为最小值的顶点相连的边都去掉，则图成为不连通图。即这些边可以构成一个割集，但未必是最小割。用δ(G)来表示图G的最小度，用C来表示最小割集，则有：

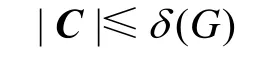
因为图G为高连通图，由其定义可得：

由此可见，高连通图的定义确保了图中的所有顶点之间都联系紧密，并且采用高连通图作为终止判据，可以无需预先知道聚类的数目，其时间复杂度和之前求最小割的复杂度一致。

2.5 聚类算法

采用2.4节建立的计算具有最小割权值和第二小割权值的图割的算法，来探索聚类结果组成的空间。给定一个无向有权图G(V, E, W)来代表数据集，分别计算出具有最小和第二最小割权值的图割。如图3(a)所示，一个数据集可以通过计算最小割权值分为2个集群。对图G计算出具有最小和第二最小割权值的图割，分别可以获取2个子图；然后对这2个子图重复应用此算法，直到所得的子图为高连通子图为止。图3(b)说明了该过程。

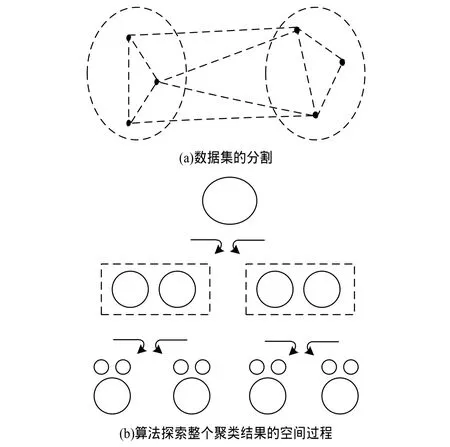
图3 聚类算法的一个示例

3 实验结果与分析

应用上述算法对2组基因芯片数据进行了测试。其中一组数据是从77例患者的肿瘤样本得到的，共包含6285个基因，这些病人中有58个为扩散型大B细胞淋巴瘤(DCBCL)患者，另外19个为滤泡淋巴瘤(FL)患者。另一组数据为原发性和转移性癌症(PM)样本，分别采自64个原发性癌患者和12个转移性癌症患者，包含了14 925个基因。在处理这2组数据集时，对式(4)中的参数做了如下取值：距离阈值T为数据点所有配对最大距离的2/3，K为最大距离平方的1/4。

与数据挖掘中通用的聚类算法相比，在对基因表达数据进行分析时更关注于算法的有效性(effectiveness)，即要求算法具有较高的准确性。因此，为了评估算法的表现，采用了一个错误率函数来计算聚类结果的准确性。考虑数据点的每对数据，并考虑它们是否在同一聚类中。如果在同一聚类中而聚类结果把它们放在2个不同的聚类中，或者反之亦然，则认为是一个错误分类。对于一个特定的聚类结果，可以计算错误分类的数目，并与成对的数目总和相除。这个错误率介于0～1之间，并可以用来衡量聚类算法的准确性。

针对本文算法的准确性，与其他一些算法做了比较，这些算法包括Fuzzy-Max，Fuzzy-Alpha，Fuzzy-Clust，Fuzzy-Single，以及Hierarchy-Single。表1和表2分别显示了在对DLBCL和PM数据的分析上，本文算法与其他算法准确性的比较结果。对于有随机性的算法，在对数据集做了多次测试后，计算了其中位误差和标准偏差。

表1 本文算法与其他算法对DLBCL数据集分析的结果比较

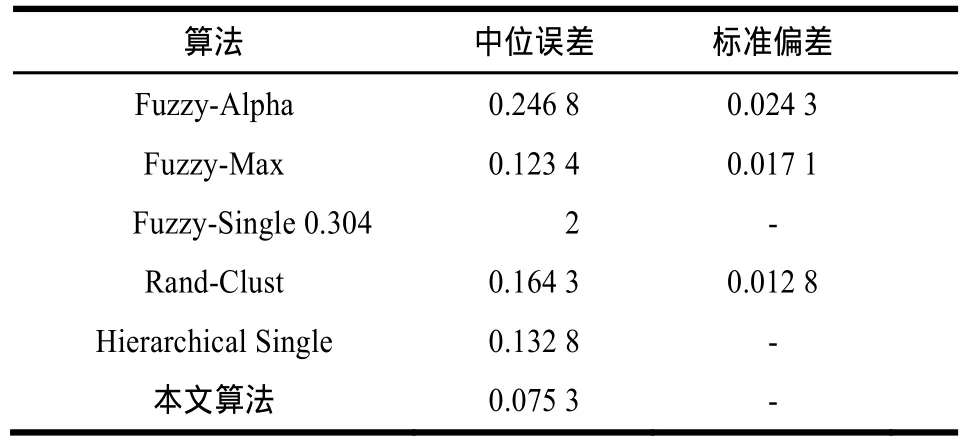
表2 本文算法与其他算法对PM数据集分析的结果比较

从表1和表2中不难发现，在上面2组数据的聚类结果中，基于图割的算法的准确性明显优于其他几种算法，而这种优势在PM数据的聚类结果中更加明显。

4 结束语

本文提出一种基于图形模型和图割算法的聚类算法，将样本空间的整个数据集表示为一个有权图，然后迭代地求解图的最小割权值和第二小割权值，根据图割将图分割为子图。测试结果表明，该算法可以有效地探测聚类结果空间，并具有较高的准确性。

下一步可以在之前研究的基础上，继续第三小割权值图割的研究：如第三小割权值图割的计算复杂度，以及其是否能进一步提高聚类精度等。另外，本文算法应用Hao 和Orlin提出的算法计算最小割，其时间复杂度为O(|V||E|))，联系第二最小割的计算，则进行一次迭代就需要O(|V||E|2)时间，其计算时间复杂度仍较高。如何降低算法计算复杂度，特别是最小割计算的复杂度，也是下一步的工作方向之一。例如：当需要分类的数据点大于1 000时，可以考虑在对DNA微阵列数据建立图形模型时，用无向无权图模型取代之前的无向有权图，即仅用两顶点的连通性来表示两基因(样本)之间的关系。到目前为止，无向无权图的全局最小割时间最低为O(|V||E|2/3)，因此可以进一步把算法总复杂度降低到O(|V||E|5/3)。

[1] 岳 峰, 孙 亮, 王宽全, 等. 基因表达数据的聚类分析研究进展[J]. 自动化学报, 2008, 34(2): 113-120.

[2] Bertoni A, V alentini G. Rand omized E mbedding Clust er Ensembles for Gene Expression Data Analysis[C]//Proc. of IEEE Internatio nal Conference on Science of Electronic, Technologies of Information and T elecommunications. Hammamet, Tunisia: IEEE Press, 2007: 246-252.

[3] Avogadri R, Valenini G. Fuzzy Ensemble Clustering for DNA Microarray Data An alysis[C]//Proc. of the 4th I nternational Conference on Bioinformatics and Biostatistics. Camogli, Italy: Springer, 2007: 537-543.

[4] Avogadri R, Valentini G. Fuzzy Ensemble Clustering Based on Random Pro jections for DNA M icroarray Data Analysis[J]. Artificial Intelligence in Medicine, 2009, 45(2): 173-183.

[5] Avogadri R, V alentini G. Ensemble Clustering with a Fuzzy Approach[M]. [S. l.]: Springer, 2008.

[6] Karypis G, Han E H, Kumar V. CHANELEON: A Hierarchical Clustering Algorithm Using Dynamic Modeling[J]. Computer, 1999, 32(8): 68-75.

[7] Estivill C V, Lee I. AU TOCLUST: Automatic Clustering via Boundary Extraction for Mining Massive Point-data Sets[C]//Proc. of the 5th International Conference on Geocomputation. Greenwich, UK: [s. n.], 2000: 23-25.

[8] Elghazel H, Yoshida T, Deslandres V, et al. A New Greedy Algorithm for I mproving B-c oloring Clustering[J]. Lecture Notes in Computer Science, 2007, 45(38): 228-239.

[9] Li Yujian. A Clustering Algorithm Based on Maximal θ-distant Subtrees[J]. Pattern Recognition, 2007, 40(5): 1425-1431.

[10] von L uxburg. A Tutorial on Spectral Clustering[J]. Statistics and Computing, 2007, 17(4): 395-416.

[11] 郑加明, 陈昭炯. 带连通性约束的快速交互式Graph-Cut算法[J]. 计算机辅助设计与图形学学报, 2011, 23(3): 399-405.

[12] Strandmark P, Kahl F. Parallel and Distributed Graph Cuts by Dual Decomposition[C]//Proc. of IEEE Conference on Computer V ision and Pattern Re cognition. San Francisco, USA: IEEE Press, 2010: 2085-2092.

[13] Candemir S, Akgul Y S. Adaptive Regularization Parameter for Graph Cut Segmentation[C]//Proc. of International Conference on Image Analysis and Recognition. Povoa de V arzim, Portugal: Springer, 2010: 117-126.

[14] James B O. A Faster Strongly Polynomial Time Algorithm for Submodular Function Minmization[J]. Mathematical Programming: Series A and B, 2009, 118(2): 237-251.

[15] Hartuv E, Shamir R. A Clustering Algorithm Based on Graph Connectivity[J]. Information Proce ssing Letters, 20 00, 76(4): 175-181.

编辑 任吉慧

Data Clustering Algorithm for DNA Microarray Based on Graph Theory

SONG Jia1,2, XU Li1, SUN Hong2

(1. Electrical Engineering College, Zhejiang University, Hangzhou 310027, China; 2. Department of Electronic and Information Engineering, Suzhou Vocational University, Suzhou 215104, China)

Clustering is an effective and practical method to mine the huge amount of DNA microarray data to gain important genetic and biological information. However, most traditional clustering algorithms can only provide a single clustering result, and are unable to identify distinct sets of genes with similar expression patterns. This paper presents an algorithm that can cluster D NA microarray data with a graph theory based algorithm. In particular, a DNA microarray dataset is represented by a graph whose edges are weighted, then an algorithm which can compute the minimum weighted and second minimum weighted graph cuts is applied to the graph respectively. Test results show that this approac h can achieve improved clustering accuracy, compared with other clustering methods such as Fuzzy-Max, Fuzzy-Alpha, Fuzzy-Clust.

microarray; gene expression data; clustering analysis; graph cut; graph theory; minimum cut

10.3969/j.issn.1000-3428.2014.05.008

江苏省自然科学基金资助项目(BK2011319)；苏州市职业大学青年基金资助项目(SZDQ09L02)。

宋 佳(1980－)，女，讲师、博士研究生，主研方向：生物信息学，智能控制；许 力，教授；孙 洪，讲师、博士。

2013-04-22

2013-05-22E-mail：sjia@jssvc.edu.cn

1000-3428(2014)05-0036-05

A

TP309