一种基于布局布线协同的PCB设计算法

闫利平，陈庆奎,2

(1. 上海理工大学光电信息与计算机学院，上海 200093；2. 上海现代光学系统重点实验室，上海 20009 3)

一种基于布局布线协同的PCB设计算法

闫利平1，陈庆奎1,2

(1. 上海理工大学光电信息与计算机学院，上海 200093；2. 上海现代光学系统重点实验室，上海 20009 3)

针对印刷电路板(PCB)设计中布局造成散热性差和布线造成抗噪声性差，导致PCB的抗干扰性弱的问题，提出一种布局布线协同算法，基于元胞自动机思想，以温度为基准，对元件进行位置调动，使元件的放置符合演化规则的定态要求，从而使布局的散热性能达到要求，同时运用优化蚁群算法对当前布局以路径最短及通孔数最小化为目标进行布线，并评价其抗噪声性能。实验结果表明，从散热性方面调整布局，散热性能提高14%左右，从抗噪声性能方面考虑布线，平均路径长度与通孔数下降明显，

PCB板的总平均温度降低14%左右。

散热性；抗噪声性；蚁群算法；元胞自动机；抗干扰性；印刷电路板设计

1 概述

抗干扰性是印刷电路板(Printed Circ uit Boar d, P CB)设计中最重要的因素。PCB设计主要涉及布局布线2个方面。设计一个抗干扰性强的PCB，要做到布局的散热性好以及布线抗噪声能力强。通过布局与布线之间相互协同，以达到上述目的。针对PCB布局布线优化设计有大量成熟的研究成果，文献[1-2]提出一种无网格布线算法，在给定布局平面上采用优化迷宫算法完成布线。文献[3-4]从布线方面考虑，解决了布线寻找最短路径及通孔数最少的问题[5]。文献[6-7]分别从启发式算法提出了布局优化的方法，文献[6]运用改进遗传算法仅对元件在布局中的位置优化并没有对元件之间干扰做出比较，文献[7]用模拟退火算法优化电子元件的布局，尽管旨在降低电子设备的最大温度值，为电子元件的散热优化问题提供了方法，但没有考虑布局单方面最优可能会造成布线布通率低及内部噪声干扰强的问题。文献[8]基于双层线板布线提出元胞蚂蚁算法对布线进行优化，但是这种布线算法计算量比较大，而且仅对已定布局适用，缺乏通过调整布局使布线路径更优的灵活性。本文从PCB抗干扰性[9-10]出发，运用布局布线的协同对PCB优化设计进行分析。提出布局与布线协同优化算法，利用基于元胞自动机思想的算法调整布局中元件的位置及蚁群算法对布线路径寻优和通孔个数控制。

2 布局布线问题描述

PCB设计主要考虑：布局和布线设计。通过布局和布线协同过程完成对PCB的设计。从布局考虑，以优化PCB散热性为目的，通过基于元胞自动机思想并遵循将不同种类的元器件分散交错排列的原则，实现对元件的合理布置；从布线考虑，运用蚁群算法对当前布局以路径最短、通孔数最小化为目的做布线设计。通过综合评估当前布局的散热性能及布线后产生噪声的大小，使得PCB设计的抗干扰性最优稳定性最好。

2.1 P CB干扰评估描述

在对PCB干扰性探讨中，主要考虑布局的散热性和布线的噪声干扰。在通常情况下，PCB抗干扰性与布局散热性呈正比，而与布线产生噪声呈反比，故PCB干扰值评估函数Dis可定义为：

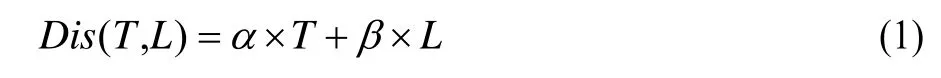
其中，α和β分别表示为布局的散热性和布线中的噪声干扰权值；T表示为布局温度衡量函数；L表示为布线噪声衡量函数。

在PCB设计中，干扰越小则稳定性越好，即可简述为：在确定T和L情况下，使得目标函数Dis( T, L)取最小值。PCB设计数学模型描述为：

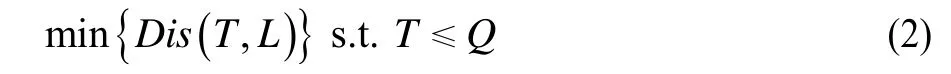
由于元件的性质不同，其产生热量及耐热值均不同，为衡量元件的温度阈值Q，通过如下公式定义：

其中，m表示元件的邻居个数；P表示元件的功率；t表示时间；d'表示两元件之间的距离；A表示分别以元件为圆心，半径为d'圆区域的重叠面积。

2.2 布局定义描述

对布局而言，考虑其散热性问题，对单个元件而言，其温度受自身和周围邻居元件热辐射[11-12]的影响，而整个PCB板的温度受板上所有元件温度的影响，PCB板的温度越高其散热性越差。因此，本文引入布局温度衡量函数T，散热性能函数K，函数T的值越大则其散热性越差即函数K的值越小，描述如下：设元件由普通元件(CE)、发热元件(HE)和热敏元件(AE)组成，令温度集合N={Tx(CE), Tx(HE), Tx(AE)}，Tx(CE)，Tx(HE)，Tx(AE)分别表示普通、发热和热敏元件的温度衡量函数，则温度衡量函数：

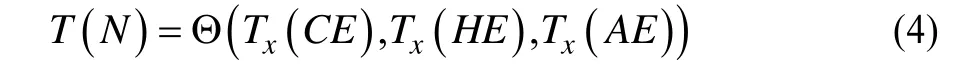
设布局散热性能函数为：

其中，µ是衡量PCB板整体温度与其散热性能关系的常量系数。

2.3 布线定义描述

对布线而言，通常是使布线路径最短，通孔数最小。由于需要对这2个目标进行优化，因此布线属于多目标优化问题，则：

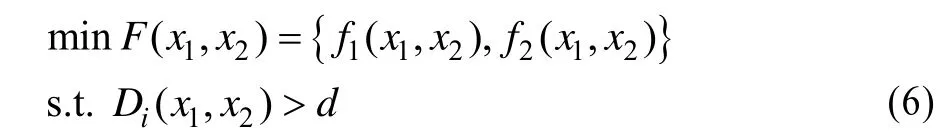
其中，x1、x2分别表示元件节点的坐标；d表示元件之间的安全距离；f1( x1, x2)表示导线产生噪声函数；f2(x1, x2)表示为通孔产生噪声函数。主要是搜索F( x1, x2)非劣解过程，求解F( x1, x2)最小值，因此，采取了蚁群这种启发式算法来解决这种多目标优化问题。

3 PCB算法设计描述

3.1 总体描述

对布局运用元胞自动机的思想实现3类元件的分散交错排列，并用函数K衡量其散热性，随之进入布线循环运用优化蚁群算法使路径最短通孔数最小化并用噪声评估函数L衡量布线的噪声影响，用式(1)对当前布局布线的干扰性进行评估。将干扰性最小的设计作为当前符合电路性能要求，稳定性高的PCB设计。

整体算法描述：

Step1初始定义存储元件温度表AT，全局温度变量Temperature；布线噪声变量Noise；状态干扰变量Ps，Ps +1；路径长度变量Length；通孔个数变量hole。

Step2定义循环变量n，设while循环迭代条件为n≤N，其中N为寻找到当前干扰性最优的布局布线设计算法执行次数的期望值；转入Step 3。

Step3调用基于元胞自动机思想的算法调整布局；根据Tx(CE)、Tx(HE)、Tx(AE)计算3种元件的温度值，存到AT中，用式(3)计算T( AT)的值并赋值给Temperature；转入Step4。

Step4调用蚁群算法对当前布局优化布线，并将最优路径长度赋给变量Length，最优通孔个数存到变量hole；调用噪声干扰评估函数式(6)衡量当前布线对整体设计的噪声干扰情况并将其赋给Noise；转入Step5。

Step5调用函数干扰值评估函数式(1)，将Temperature值和Noise值分别传到T、L中，衡量整体设计的干扰值并赋值给Ps；转入Step3；可获得下一个状态干扰的衡量值Ps+1，然后比较即ifPs＞Ps +1，then将Ps+1赋给Ps，使n=n+1；else转入Step3 并执行n=n+1；if n≤N，then 转入 St ep2；else 结束循环。

3.2 布局实现算法

3.2.1 元胞自动机演化规则描述

设四元组集合A={Ld, S, M, f }，定义Ld( d=2)表示二维空间，S表示任意元件状态转移的状态集合S={上移(Sa)，下移(Sd)，左移(Sl)，右移(Sr)，左上移(Sla)，左下移(Sld)，右上移(Sra)，右下移(Srd)，定态(Sw)}，状态转移标志用0、1表示。当允许转移时置状态标志变量Flag为1，其他为0，M表示元件邻居集合M={M1,M2,…,Mi}，i表示邻居节点个数，f是状态的演化规则，其定义如下：由于当前布局每个元件受邻居元件热辐射及其自身温度影响，其目标函数：

(1)在上下左右4个方向都有元件的情况下，对于上移(Sa)状态转移的定义：对中心元件相邻位置正下方元件对其热辐射的温度Ts判断，若Ts＞Q，则状态转移标志Flag= 1，对应元件向上移动，同时将Flag清0，并判断此次位置调整后该元件对邻居元件影响是否大，若在影响允许范围内则接受当前调整，否则判断其他方向的元件。

同理，对状态集合S中其他状态即下移(Sd)、左移(Sl)、右移(Sr)进行位置调整。

(2)在斜对角4个方向情况下，对于左上移(Sla)状态转移的定义：对中心元件相邻位置正右、下、右下方3个元件对其热辐射的温度之和sT判断，运用和(1)同样的方法。

同理，对状态集合S中其他状态即左下移(Sld)、右上移(Sra)、右下移(Srd)用同样的方法调整。

(3)对于状态集合S中定态(Sw)的定义：若对上述8种情况均判断不满足条件，则是定态(Sw)的标志变量Flag置1，表示该元件不需要移动。

3.2.2 布局算法描述

布局算法步骤如下：

Step1设一个状态集合为S，初始状态转移标志Flag均为0，当Flag为1时则选取该状态，存储邻居元件节点的集合M={M1,M2,…,Mi}。

Step2从温度表AT中取出当前中心元件温度值，判断其温度及邻居元件对其的影响，并改变状态集合中相应Flag的值，根据f，实现布局的调整。

Step3设Ni( xi, yi)为第i个元件的坐标，根据邻居集合M计算中心元件No(xo. yo)到邻居元件Ni( xi, yi)的距离：

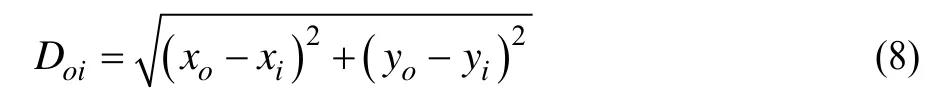
To、Ti分别表示中心元件及邻居元件的温度，根据公式：

其中，T(s)表示当前状态温度，返回温度值Temperature= T( s)，并存储Temperature。

3.2.3 布线算法描述

蚁群算法被证明在多目标优化问题上，表现出很好的并行特性和鲁棒性，并且成功地用于求解多种NP难的问题，以下给出蚁群算法描述：

Step1设时刻变量time置0；迭代步数nc置0，对各边D(i,j)：置τij为常数c(c趋于无穷小)；置Δτij为0；Lbest置空(储存当前最好的路径队列)；hole置0存储通孔个数；置Length常数a(a是较大的正数，Length用来储存当前最短的路径长度)。

Step2将m只蚂蚁随机置于n个结点上；对于每个蚂蚁：初始化禁忌表；置空路径队列Lbest。

if 边E(i,j)上没有障碍，then移动蚂蚁k至结点j than else 调用避障程序；

if 选择通孔，则hole++；than else避线绕点；

j加入禁忌表；Dij置入队列Lengthk；end计算路径Lengthk长度，将最好的结果存入Lbest。

Step3for k=1 to m

Step4if nc ＜预定迭代次数且无退化行为，则循环结束。

4 实验结果与分析

4.1 布局散热测试

在NS2中对网络规模为20的拓扑结构仿真，并用CFD软件对整个拓扑结构进行热分析。通过对优化布局前后结点平均温度的对比验证该方法的优越性。分析如图1所示。图1显示了布局优化前后各元件平均温度的对比。经计算比较得，优化后平均温度低于优化前的平均温度，整体性能提高14%。

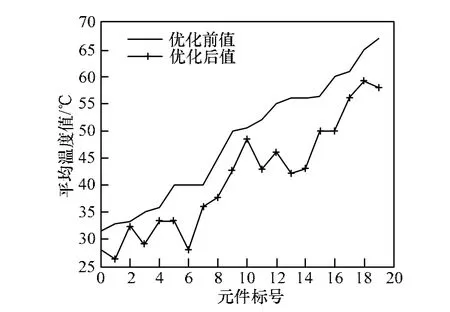
图1 布局优化前后对比

4.2 布线实验

布线结果从不断增加布局元件个数的角度出发，突出了这种布线算法的优越性，结果如图2所示。实验通过不断增加PCB板元件的个数来验证。图2显示了随着元件的增多布线路径长度个数及通孔个数的优化率在不断提高，元件个数相当大时通孔个数的优化率明显高于路径长度的优化率；当元件个数增加到一定程度基本趋于一个稳定状态下的优化。

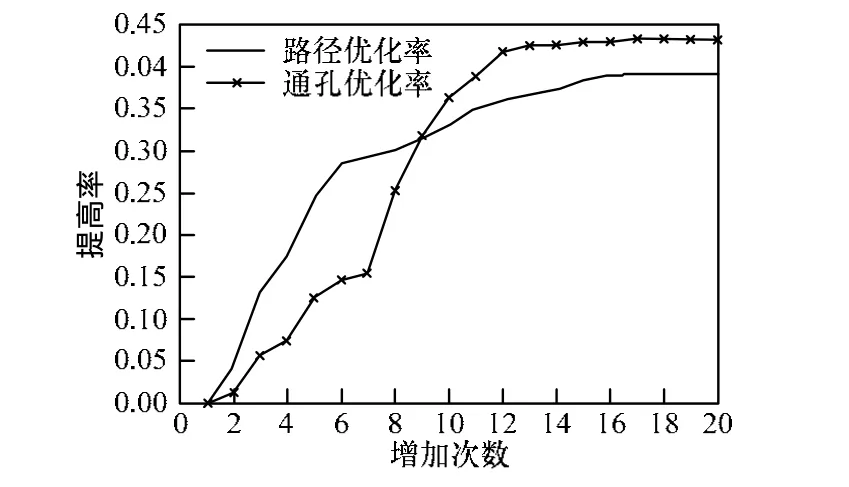
图2 布线优化过程

4.3 干扰性测试

本次实验从布局布线2个方面表现PCB干扰性的大小，图3表示每1 s后抽取一次优化布局后PCB板的总体平均温度值，如图描绘出每1 s后对PCB整体温度的观测，随着对布局的优化，其总体平均温度呈现下降趋势，起初每隔1 s的下降趋势很平缓，随着时间的增长其总体平均温度下降很明显，总体下降幅度约20%。

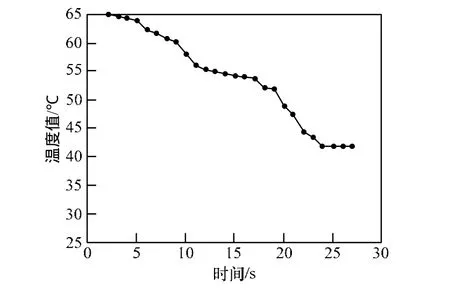
图3 布局优化后总平均温度变化

布线优化后的平均噪声值如图4所示。

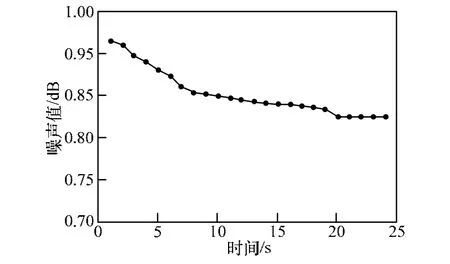
图4 布线优化后的平均噪声值

图4表示每1 s后优化布线产生噪声值的优化情况，整体走势：在10 s之前平均噪声值下降幅度大约0.008 dB/s，10 s之后下降幅度比较平缓，当达到平衡状态时其平均温度也随着达到平衡，整体的温度平均下降14%左右，运用式(1)可以计算出在20 s左右干扰值趋于较小，直到布线达到一个平衡状态时设计达到最优。

在基于20台刀片服务器模拟20个元器件情况下，将本文算法与当前经典布局布线算法进行比较，如表1所示。

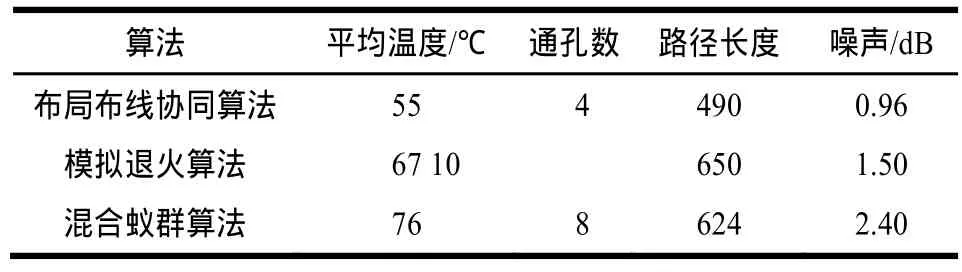
表1 算法性能比较

5 结束语

本文提出了一种基于布局布线协同的PCB设计算法，主要是围绕基于元胞自动机的思想对PCB上的元件设计布局，协同运用优化蚁群算法设计布线，平衡布局的散热性能和布线的抗噪声干扰，使设计的PCB具有较强的抗干扰性。实验结果证明了算法的有效性，今后将进一步对PCB设计中影响抗干扰性能的电磁干扰源进行研究，以适应电子行业与时俱进的发展要求。

[1] 王书江, 葛海通, 严晓浪. 超大规模集成电路无网格布线算法研究[J]. 电路与系统学报, 2002, 7(4): 13-16.

[2] 谢满德. 一种自适应多层无网格布线算法[J]. 计算机工程, 2006, 32(14): 11-13.

[3] 黄训诚, 庄奕琪, 耿阿囡. 基于粒子群优化算法的集成电路无网格布线[J]. 西安电子科技大学学报, 2007, 34(1): 34-37.

[4] 马 力, 张忠涛, 张 妍. 高速电路PCB布线中参考层的设计与实现[J]. 计算机工程, 2008, 34(增刊): 88-92.

[5] 邹志强. 嵌入式双Pentium Ⅲ单板的高速PCB设计[J].计算机工程, 2003, 29(9): 163-165.

[6] 刘孝保, 杜平安. 面向元器件的PCB板布局优化方法[J].电子科学技术大学学报, 2011, 40(4): 630-633.

[7] 王玉兰, 云和明. 基于退火算法的PCB电子元件散热布局优化分析[J]. 信息技术与信息化, 2007, (1): 75-77.

[8] 鲁宇明, 黎 明, 李 凌. 一种具有演化规则的元胞遗传算法[J]. 电子学报, 2010, 38(7): 1603-1609.

[9] 畅艺峰, 杨银堂. 多芯片组件布局布线设计的新途径[J].西北大学学报: 自然科学版, 2006, 36(4): 547-550.

[10] Hanreich G, Nicolics J, M usiejovsky L. High Resolution Thermal Simulation of Electronic Compone nts[J]. Microelectronics Reliability, 2000, 40(12): 2069-2076.

[11] Zhao C Y, Kim T. Modeling on Thermal Trans- port in Cellular Metal Foams[C]//Proc. of Joint Thermo Physics and Heat Transfer Conference. St. Louis, USA: [s. n.], 2002.

[12] Wen T, Tian J, Lu T J, et a l. Forced Convection in Metallic Honeycomb S tructures[J]. Interna tional Journal of Heat and Mass Transfer, 2006, 49(19/20): 3313-3324.

编辑 顾逸斐

A PCB Design Algorithm Based on Collaboration Between Layout and Wiring

YAN Li-ping1, CHEN Qing-kui1,2

(1. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China; 2. Shanghai Key Lab of Modern Optical System, Shanghai 200093, China)

It is the problem that weak immunity of Printed Circuit Board(PCB) resulted by the low thermal dissipation performance with unreasonable layout and the low noise immunity performance w ithout optimization wiring. To attack the problem, an al gorithm based on collaboration between the layo ut and the wiring is proposed. The algorithm adopts the rule based on Cellular Automata(CA) transfers the position of components according to temperature limitat ion for layout so that the h eat dissipation performance of layout can be more reasonable and the method is proposed based on Ant Colony Algorithm(ACA) looks for the shorte st routing length and the minimum number of holes and evaluates PCB noise immunity performance for wiring. Experimental result shows that performance of heat dissipation is increased by 14% on the aspect of heat dissipation for the layout, the average routing length and number of holes are decreased obviously on the aspect of noise immunity for the wiring and the PCB total average temperature is decreased by 14%.

heat dissipation; noise immunity; Ant Colony Algorithm(ACA); cellular automata; interference immunity; Printed Circuit Board(PCB) design

10.3969/j.issn.1000-3428.2014.05.064

国家自然科学基金资助项目(60970012)；教育部博士学科点专项科研博导基金资助项目(20113120110008)；上海教委创新基金资助重点项目(13ZZ112)；上海信息技术领域重点科技攻关计划基金资助项目(09511501000, 09220502800)；上海市教育科学研究基金资助项目(B11042)；上海市一流学科建设基金资助项目(XTKX2012)。

闫利平(1990－)，女，硕士研究生，主研方向：电路设计；陈庆奎，教授、博士、博士生导师。

2013-03-18

2013-05-17E-mail：yanliping1990@sohu.com

1000-3428(2014)05-0309-04

A

TP314