一种贝叶斯网络结构学习的混合随机抽样算法

2014-08-05胡春玲胡学钢

计算机工程 2014年5期

关键词：子结构后验概率分布

胡春玲，胡学钢，吕刚

(1. 合肥学院网络与智能信息处理重点实验室，合肥 230 602；2. 合肥工业大学计算机与信息学院，合肥 23000 9)

一种贝叶斯网络结构学习的混合随机抽样算法

胡春玲1，胡学钢2，吕刚1

(1. 合肥学院网络与智能信息处理重点实验室，合肥 230 602；2. 合肥工业大学计算机与信息学院，合肥 23000 9)

贝叶斯网络结构学习的随机抽样算法存在收敛速度慢的问题，为此，结合均匀抽样和独立抽样，从初始样本、抽样方式和建议分布3个方面对抽样过程进行改进，提出一种混合型马尔可夫链蒙特卡罗抽样算法(HSMHS)。基于节点之间的互信息生成网络结构的初始样本，在迭代抽样阶段，按一定的概率随机选择均匀抽样和独立抽样，并根据当前抽样的样本总体计算独立抽样的建议分布，以改善抽样过程的融合性，加快收敛速度。对算法进行正确性分析，证明其抽样过程收敛于网络结构的后验概率分布，可保持较高的学习精度。在标准数据集上的实验结果表明，HSMHS算法的学习效率和精度均高于同类算法MHS、PopMCMC 和Order-MCMC。

贝叶斯网络；结构学习；随机抽样；混合抽样；子结构抽样；建议分布

1 概述

贝叶斯网络模型是一种可以处理不确定性问题最有效的概率模型之一。如何从数据中学习贝叶斯网络一直是具有挑战性且非常活跃的研究领域[1-2]。贝叶斯网络的结构学习算法主要分为基于评分-搜索和基于依赖分析的学习算法[3-4]，基于评分-搜索的学习算法存在可能收敛于局部最优解的问题，而基于依赖分析的算法存在独立性判断困难等问题，这两类算法都是按照所选择的评价标准学习一个最优的贝叶斯网络结构，而高维小样本的数据集D本身就具有多个服从其后验概率分布P( s| D)的网络结构s，因此，学习一个最优网络结构的点估计类学习算法通常不能提供可靠的学习结果。

马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法[5-6]是一类重要的处理复杂问题的随机抽样方法，该方法通过构建一条收敛于目标平稳分布的马尔可夫链，得到目标平稳分布的样本，通过样本对平稳分布的特性进行估计。MHS(Metropolis-Hasting Sampler)抽样算法[7]是MCMC方法中常用的算法之一，文献[8]将这一抽样算法引入贝叶斯网络结构学习，采用局部的弧增加、删除和反向的均匀分布作为抽样过程的建议分布，利用抽样过程产生的来自目标平稳分布的网络结构样本来估计贝叶斯网络的结构特征，但MHS算法存在抽样过程融合性差、收敛速度慢的问题。为此，不同的改进算法相继被提出[9-11]，其中具有代表性的是针对节点序抽样的Order-MCMC算法[10]和基于样本总体抽样的PopMCMC抽样算法[11]。Order-MCMC算法假设不同节点序的先验概率服从均匀分布，符合较多节点序的网络结构先验概率较高，先验概率不均匀分布会给网络结构的后验概率估计带来偏差，导致学习结果的不准确。PopMCMC抽样算法基于抽样所得样本总体来学习抽样过程的建议分布，当所得的样本总体的分布不能很好地近似网络结构的后验概率分布时，抽样过程的接收率很低，收敛速度不能得到有效改善。贝叶斯网络结构学习的MHS抽样算法能够较好地解决进化学习方法中由于个体趋同而产生的早熟问题，提高学习精度，但该类算法存在的收敛速度慢问题仍未能得到有效解决。初始值、建议分布和抽样方式是影响MHS类算法抽样过程收敛速度的重要因素。

本文通过对MHS算法的初始样本、建议分布和抽样方式的设计，提出一种混合型包含子结构抽样的MHS算法(HSMHS)。首先基于节点之间的互信息在缩减的网络结构状态空间中生成初始样本，然后在其迭代抽样阶段，采用混合型的抽样算法，即按一定的概率分布，随机选择均匀抽样和独立抽样2种抽样算法进行抽样，独立抽样的建议分布采用来自当前样本总体的边和子结构的后验概率，并在独立抽样中增加了对网络子结构的抽样，以改善抽样过程的融合性。

2 MHS抽样算法

为了叙述方便，本文采用X={X1,X2,…,Xn}表示领域变量；D表示训练数据集；Par( Xi)为网络结构s中节点Xi的父节点集。

贝叶斯网络结构学习的MHS算法的建议分布采用弧添加、删除和反向的均匀分布作为抽样过程的建议分布，构建一条平稳分布为网络结构s的后验概率分布P( s| D)的马尔可夫链，然后通过收敛之后的马尔可夫链抽样产生样本来估计待学习贝叶斯网络的结构。MHS算法的抽样迭代过程如下：

(1)记网络结构的当前状态为s(c)，采用弧添加、删除和反向的均匀分布作为建议分布R( s(n)|s(c))，生成网络结构的下一个状态s(n)。

(2)新生成的网络结构(n)s的接收概率计算公式为：

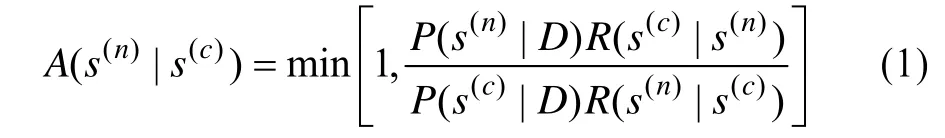
其中，P( s| D)为网络结构的评分，本文采用网络结构的BDe评分[12]，则网络结构的转移概率为：

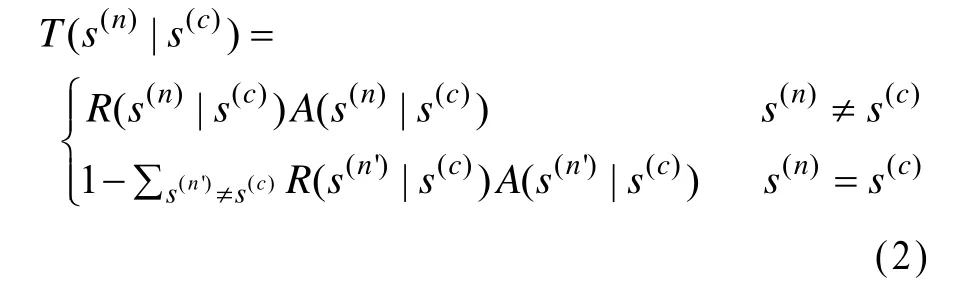
(3)以概率A( s(n)|s(c))接收新网络结构s(n)取代原有网络结构s(c)；以概率1-A( s(n)|s(c ))拒绝接收新网络结构s(n)，此时保留原有网络结构s(c)。

(4)重复以上步骤，直到迭代过程收敛。

3 HSMHS抽样算法

初始值、建议分布和抽样方式是影响抽样算法收敛速度的重要因素。如果初始值和目标分布的距离很小，抽样过程的收敛速度会很快；若建议分布近似于目标平稳分布，此时的抽样过程近似于目标平稳分布的独立抽样，具有较快的收敛速度。HSMHS算法通过对初始值、建议分布和抽样方式的设计来改善抽样过程的收敛速度。HSMHS算法首先基于节点之间的互信息，在缩减的状态空间中进行网络结构样本的初始化，然后进入迭代抽样阶段；迭代抽样阶段采用按照一定的概率分布随机选择均匀抽样和独立抽样的混合抽样方式，其中独立抽样又包括弧抽样和子结构抽样，弧抽样和子结构抽样的建议分布均为当前抽样样本总体中弧和子结构的后验概率估计。重复这一抽样过程，直到构建马尔可夫链收敛于目标平稳分布：网络结构的后验概率分布P( s| D)。

3.1 初始化

互信息度量了节点之间依赖程度[13]，如果节点之间的互信息小于给定的阈值ε，网络中对应节点之间不存在边。互信息的计算公式如下：

当数据集完备时，可以通过一遍扫描数据库，得到式(3)中互信息计算所需的概率参数。

HSMHS算法根据节点之间互信息I( Xi,Xj)和预先给定的阈值ε，去掉在网络结构中不存在的边，减小网络结构的搜索空间，生成网络结构的初始样本，该算法首先通过最大生成树算法，生成初始样本中一个网络结构，然后在缩减的网络结构状态空间中，采用随机生成的方法产生初始样本中的其他网络个体，所生成的初始样本比完全随机生成的样本更加接近于该网络结构的后验概率分布P( s| D)。

3.2 迭代抽样

算法HSMHS的迭代抽样过程按照一定的概率随机选择独立抽样和均匀抽样。均匀抽样的建议分布为弧添加、删除和反向的均匀分布。独立抽样的性能取决于所选择的抽样方式和建议分布。进化学习在其迭代过程中总是希望好的基因块能够在下一代的个体中保留下来，以减少学习过程的迭代次数，对应到网络结构的抽样学习算法中，就是希望评分高的网络子结构能够在下一代的个体中保留下来，因此，为了改善抽样过程的融合性，HSMHS算法在其独立抽样过程中增加了子结构抽样方式。独立抽样的建议分布等于目标平稳分布时，抽样效果是最优的，但在实际抽样问题中，目标平稳分布事先并不知道，事实上，只要选择能够较好近似于目标分布的建议分布，则根据式(1)计算的接收概率近似为1，此时独立抽样对于拒绝评分低的网络结构非常有效，其抽样过程具有较高的接收率和较好的融合性。

综上，HSMHS算法的具体步骤如下：

(1)初始化：基于节点之间的互信息，在缩减的网络结构状态空间中，采用最大生成树算法和随机算法生成网络结构的初始样本(互信息阈值ε通常取值为0.001,0.05,0.1)。

(2)迭代阶段：按概率(ξ， 1-ξ)随机选择独立抽样和均匀抽样(0.1ξ0.5）≤≤。

1)若为均匀抽样，则从当前总体中随机选择个体进行弧抽样，弧抽样的建议分布为均匀分布，按式(1)计算新个体的接收概率。

2)若为独立抽样，则按均匀分布进一步选择弧抽样和子结构抽样：

①若为弧抽样，则从当前总体中随机选择个体进行弧抽样，弧抽样的建议分布为按式(4)计算的当前总体中该弧后验概率估计，按式(1)计算新个体的接收概率。

②若为子结构抽样，则从当前总体中随机选择个体进行子结构抽样，子抽样的建议分布为按式(5)计算的当前总体中该子结构后验概率估计，按式(1)计算新个体的接收概率。

直到算法收敛或已达到预计的迭代次数。算法执行过程中会对生成网络结构是否满足有向无环特性进行检测，若网络结构非法，则定义式(1)中P( s(n))为0。

4 正确性分析

随机抽样算法必须保证其抽样过程的遍历性和可逆性，并最终保证抽样过程收敛于目标平稳分布。以下定理证明了HSMHS算法抽样过程满足可逆性，并最终收敛于网络结构的后验概率分布P( s| D)。

定理1HSMHS算法的抽样过程满足局部可逆性，即满足：

证毕。

定理2HS MHS算法的抽样过程收敛于网络结构的后验概率分布P( s| D)，即满足：

证毕。

HSMHS算法通过对目标平稳分布抽样产生样本总体来学习贝叶斯网络的结构，比学习一个最优网络结构的学习算法具有更高的稳定性和学习精度。HSMHS算法是一种按照一定概率分布随机选择均匀抽样和独立抽样的混合抽样算法，其均匀抽样有助于在最优解附近发现服从网络结构后验概率分布P( s| D)的网络个体，独立抽样基于当前的抽样样本总体计算建议分布，其建议分布能较好近似于网络结构的后验概率分布并具有自适应性，独立抽样还通过子结构的抽样来进一步改善抽样过程的融合性，以提高抽样过程的收敛速度。以下在标准数据集上的实验结果验证了HSMHS算法能有效提高其抽样过程的收敛速度，具有良好的学习效率和学习精度。HSMHS算法采用二维数组存储贝叶斯网络结构，如果样本长度为k，网络中的节点个数为n，该算法的空间复杂度为O(kn2)。

5 实验与结果分析

Alarm网络(37个节点)是用来测试贝叶斯网络学习算法的标准网络。根据网站http://www.norsys.com提供的Alarm网概率分布表生成具有2 000个实例的训练数据集，在针对Alarm网络的实验中，MHS、PopMCMC和HSMHS算法抽样过程的迭代次数为300 00 0次，OrderMCMC是基于节点序的抽样，一次抽样所需时间约为基于网络结构抽样的10倍，对应的OrderMCMC算法迭代次数约为30 000次，抽样过程产生的样本大小为30，HSMHS算法中独立抽样的概率ξ=0.2，节点之间互信息的阈值ε=0.001。

算法的收敛速度是衡量随机抽样算法性能的一个重要指标，针对Alarm数据集，本文比较了HSMHS算法和同类算法MHS、PopMCMC、OrderMCMC的收敛速度。图1是在有2 0 00条实例Alarm数据集上，HSMHS、MHS、PopMCMC和OrderMCMC算法收敛速度的比较，该图中纵坐标表示网络结构的BDe评分(真实Alarm网络在该数据集上的BDe评分为–21 945)，图中从下到上曲线分别表示算法MHS、OrderMHS、PopMCMC和HSMHS的迭代过程。可以看出，HSMHS在迭代50 00 0次左右即收敛，其收敛速度明显优于MHS和PopMCMC算法，一定程度上优于OrderMCMC算法，验证了HSMHS算法在改善抽样过程收敛速度方面所具有的优势。

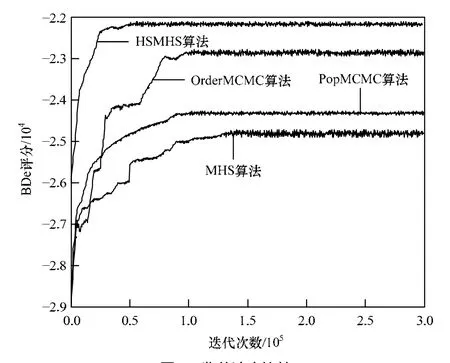
图1 收敛速度比较

HSMHS算法的均匀抽样采用均匀分布作为建议分布，有助于从目标分布附近去发现属于目标分布的个体；HSMHS算法的独立抽样在保证抽样过程收敛性的前提下其建议分布能够越来越好地近似于目标分布，抽样过程具有自适应性，结合子结构的抽样方式可改善抽样过程的接收率和融合性，因而可提高抽样过程的收敛速度。

受试者工作特性(Receiver Operating Characteristic, ROC)曲线是以真阳性率(灵敏度)为纵坐标，假阳性率(1-特异度)为横坐标绘制的曲线，曲线下方的面积表示结构学习算法的学习精度，面积越大，学习的精度就越高。图2是MHS、PopMCMC、OrderMCMC和HSMHS算法针对2 000个实例的Alarm数据集，在300 000迭代过程结束后的ROC曲线比较，其中HSMHS和PopMCMC算法迭代过程结束后所产生样本的ROC曲线，而MHS 算法取其迭代过程最后产生的30个个体的ROC曲线，OrderMCMC算法取其迭代过程最后产生的30个个体的对应网络结构的ROC曲线，该图中算法名下的数值对应于不同ROC曲线下的面积，代表相应算法的学习精度，可以看出，HSMHS算法的学习精度最高。

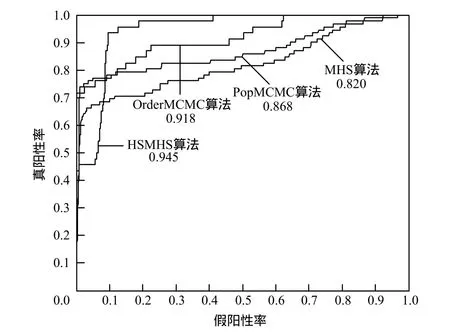
图2 学习精度比较

6 结束语

随机抽样算法具有良好的学习精度，但面临着抽样过程收敛速度慢的问题。本文提出的HSMHS算法从初始样本、抽样方式和建议分布3个方面对MHS抽样算法进行改进，以提高抽样的收敛速度。HSMHS算法的抽样过程能够收敛于网络结构的后验概率分布，因而具有良好的学习精度，在标准数据集上的实验结果也证明了该算法的有效性。针对高维小样本的生物信息数据，后续工作将围绕如何有效地将HSMHS算法应用于基因调控网络的建模。

[1] Chickering D M, Heckerman D, Meek C. Large-sample Learning of Bayesian Networks is NP-Hard[J]. Machine Learning Research, 2004, 5(1): 1287-1330.

[2] Acid S, de Campos L M, Fernández M. Score-based Methods for Learning Markov Bundaries by Searching in Constrained Spaces[J]. Data Mining and Knowledge Discov ery, 2 013, 26(1): 174-212.

[3] Wong M L, Leung K S. An Efficient Data Mining Method for Learning Bayesian Networks Using an Evolutionary Algorithmbased Hybrid Approach[J]. IEEE Transactions on Evolu tionary Computation, 2004, 8(4): 378-404.

[4] 胡春玲. 贝叶斯网络结构学习及其应用研究[D]. 合肥:合肥工业大学, 2011.

[5] Soliman A A, Abd-Ellah A H, Abou-Elheggag N A. Modified Weibull Model: A Bayes Study Using M CMC Approa ch Based on Progressive Censoring Data[J]. Reliability Engineering & System Safety, 2012, 100(4): 48-57.

[6] 曹飞凤. 基于MCMC方法的概念性流域水文模型参数优选及不确定性研究[D]. 杭州: 浙江大学, 2010.

[7] Hou Yunshan, Huang Jianguo, Jin Yong. Fast Algorithm for Bayesian DOA Estimator Based on Metropol is-Hastings Sampling[J]. Journal of System Simulation, 2009, 21(19): 6033-6072.

[8] Madigan D, York J. Bayesian Graphical Models for Discrete Data[J]. International Statisti cal Review, 19 95, 6 3(2): 215-232.

[9] 胡春玲, 胡学钢. 一种基于随机抽样的贝叶斯网络结构学习算法[J]. 2009, 计算机科学, 36(2): 199-202.

[10] Friedman N, Koller D. Being Bay esian About Network Structure: A Ba yesian Ap proach to Structure Discovery in Bayesian Networks[J]. Machine L earning, 2003, 50(1/2): 95-125.

[11] Myers J W. Population Markov Chain Monte Carlo[J]. Machine Learning, 2003, 50(1/2): 175-196.

[12] Heckerman D, Geiger D, Chickering D M. Learning Bayesian Networks: The Combination of Knowledge and Statistical Data[J]. Machine Learning, 1995, 20(3): 197-243.

[13] Cheng J, Greiner R, Kelly J. Learning Bayesian Networks from Data: An Efficient Information-t heory Based Approach[J]. Artificial Intelligence, 2002, 137(1/2): 43-90.

编辑金胡考

A Hybrid Stochastic Sampling Algorithm for Bayesian Network Structure Learning

HU Chun-ling1, HU Xue-gang2, LV Gang1

(1. Key Laboratory of Network and Intelligent Information Processing, Hefei University, Hefei 230602, China; 2. School of Computer and Information, Hefei University of Technology, Hefei 230009, China)

According to slow convergence speed of stochastic sampling algorithm, based on uniform sampler and independent sampler, by improving convergence speed from the initial sample, sampling method and proposal distribution, a hybrid markov chain Monte Carlo sampling algorithm(HSMHS) is put forward in this paper. Based on mutual information between network nodes, it generates initial samples of network structure. In iteration sampling phase, according to certain probability distribut ion, it randomly selects un iform sampler or independent sampler, and computs proposal distribution of independent sampler based on the current samples to improve the mixing of sampling process. It can be proved that sampling process of HSM HS converges to the posterior probability of network structure, and the algorithm has a good learning accuracy. Experimental results on standard data set also verify that both l earning efficiency and precision of HSMHS outperform classical algorithms MHS, PopMCMC and Order-MCMC.

Bayesian network; structure learning; stochastic sampling; hybrid sampling; sub-structure sampling; proposal distribution

10.3969/j.issn.1000-3428.2014.05.049

国家自然科学基金资助项目“基于协同训练策略的不完全标记数据流分类问题研究”(61273292)；安徽省自然科学基金资助项目“面向若干复杂场景的水平集图像分割关键技术研究”(1308085MF84)；合肥学院人才基金资助项目“基于多数据源和概率图模型的基因调控网络建模与分析研究”(1308085MF84)。

胡春玲(1970－)，女，副教授、博士，主研方向：贝叶斯网络，数据挖掘；胡学钢，教授、博士、博士生导师；吕刚，副教授、硕士。

2013-02-20

2013-05-17E-mail：huchunling8787@aliyun.com

1000-3428(2014)05-0238-05

TP18

·多媒体技术及应用·