GB-Radar与测量机器人数据融合方法研究

岳建平，曾宝庆，郭腾龙，董 杰

(河海大学地球科学与工程学院，江苏南京 210098）

GB-Radar与测量机器人数据融合方法研究

岳建平，曾宝庆，郭腾龙，董 杰

(河海大学地球科学与工程学院，江苏南京 210098）

一、引 言

测量机器人(georobot）是一种能代替人进行自动搜索、跟踪、辨识和精确照准目标并获取角度、距离、三维坐标及影像等信息的电子全站仪，亦称测地机器人[1]。测量机器人应用灵活，适用于多种监测环境和变形体，但该系统采样频率和空间分辨率低，观测时间长，实时性和同步性差，难以满足大范围快速、高精度形变监测的要求[2-4]。

基于GB-Radar的IBIS-S系统，通过微波探测主动成像方式获取监测范围内的变形数据，利用步进频率连续波技术提高雷达的距离向分辨率，通过干涉技术实现沿雷达视线向优于毫米级的微变形监测[5-8]。GB-Radar具有高空间分辨率、高采样频率和高监测精度等特点，更适合大面积、多测量点的变形监测环境，且能对监测目标进行实时动态监测，但该系统只能得到雷达视线向的一维变形量[9-12]，与工程实际需要的三维变形不一致，因此，有必要将视线向的一维变形量通过一定的数学方法转化为工程需要的三维变形量。

本文研究GB-Radar与测量机器人的监测数据的配准和融合方法，以期得到工程所需的高精度的三维变形量。

二、数据配准

数据配准是将两个或两个以上坐标系中的三维空间数据转换到统一坐标系统中的数学计算过程。测量机器人观测量是三维变形量，GB-Radar观测量是雷达视线向的一维变形量(LOS），为进行两种系统监测量配准，需要探讨两种坐标系之间的转换关系。

图1为GB-Radar坐标系OLBH和测量机器人测站坐标系OXYZ的空间关系。变形量是相对值，与原点位置无关，因此，可以将两种坐标系原点平移至同一点。

图1 GB-Radar坐标系OLBH和测站坐标系OXYZ的空间关系

测站坐标系OXYZ以测站点为原点，X轴指向零方向并平行水平面，Z轴指向天顶距方向，Y轴垂直于X轴和Z轴形成的平面构成右手系。GBRadar坐标系OLBH以雷达天线中心为原点，雷达视线向为B轴，L轴垂直B轴并且平行水平面，H轴垂直于L轴和B轴形成的平面构成右手系。α为雷达视线向在XOY面的投影与测站坐标系Y轴的夹角，β为雷达视线向B轴与测站坐标系Z轴的夹角。

GB-Radar观测到的一维变形量在GB-Radar坐标系OLBH下用[0ΔBg0]T表示，测量机器人观测到的三维变形量在测站坐标系OXYZ下用[ΔXΔYΔZ]T表示，将测站坐标系下的三维变形量[ΔXΔYΔZ]T转换为GB-Radar坐标系下的三维变形量[ΔLrΔBrΔHr]T，转换关系如下

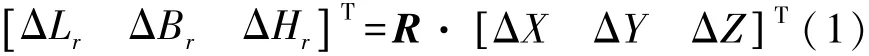
式中，R为三阶旋转矩阵，如图1可知，两坐标系只有两个旋转参数α和(90°-β），将坐标系OXYZ绕Z轴顺时针旋转α角，再将坐标系OXYZ绕X轴逆时针旋转(90°-β）角，则两坐标系经过两次坐标轴旋转完全重合。根据坐标系旋转关系，式(1）的旋转矩阵为

式中，α与β可由GB-Radar雷达天线中心和监测点连线构成的向量在测站坐标系OXYZ中的坐标计算得到。将旋转矩阵R代入式(1）可将测站坐标系OXYZ三维变形量转换为GB-Radar坐标系OLBH的三维变形量。

测站坐标系OXYZ三维变形量转换为GBRadar坐标系OLBH的三维变形量数学关系如式(1）所示，通过旋转矩阵R可完成两种不同坐标系监测数据坐标基准的统一，为两种监测数据的融合奠定了数学基础。

三、数据融合方法

GB-Radar观测值为一维变形量，测量机器人观测值为三维变形量，故两种监测系统只有雷达视线方向(即B方向）的变形量可利用最小二乘估计进行融合。

数据配准后，设GB-Radar在B方向观测值为ΔBg，观测误差为Δg，测量机器人B方向观测分量为ΔBr，观测误差为Δr。若在一个GB-Radar观测周期内的实际变形值为ΔB，则GB-Radar观测量基础方程为

式中，Wg、Wr为系数矩阵；σ0为单位权中误差；Qg、Qr为协因数；Pg、Pr为权。

计算ΔB的最小二乘估计值Δ＾B，就是使如下的关系式达到最小值

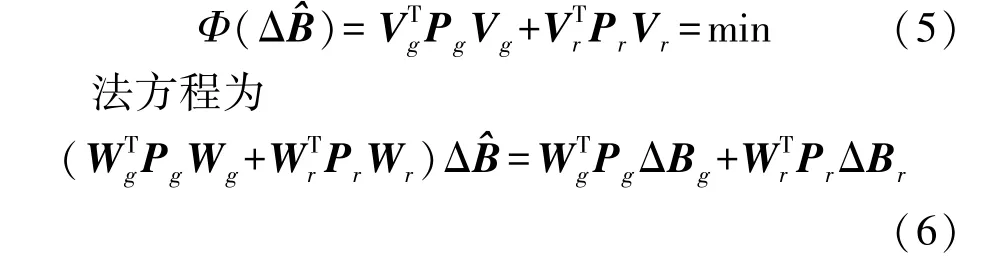
对于单个测点的情况，有Wg＝Wr＝I，I为单位矩阵，则可求得最小二乘估计值

测量机器人在OLBH坐标系下B方向的变形分量用式(7）计算得到的最小二乘估计值Δ＾B来代替，则测量机器人在坐标系OLBH下的三维变形量为[ΔLrΔ＾BΔHr]T，最后把该三维变形量变换到测站坐标系

式(8）中的[ΔXΔYΔZ]T即为融合后的测站坐标系OXYZ下的三维变形值。

四、数据融合模型应用

为了检验融合方法的有效性，设计试验获取测量机器人和GB-Radar监测数据，采用文中所述的最小二乘估计法进行融合，然后对融合后的数据进行分析。

1.试验设计

本次试验采用IBIS-S系统和索佳NET05测量机器人为监测仪器。试验中用金属三面角反射器(3个可移动角反射器CR1、CR2、CR3）作为监测点，角反射器距离监测仪器50 m以内，IBIS-S系统采用静态观测模式。试验过程分两个阶段，按表1所述的移动方案，利用安装在角反射器的游标卡尺(精度为0.02 mm）精确移动角反射器(远离仪器）。IBIS系统每次监测2 min，同时利用测量机器人对角反射器采用全圆观测法观测3测回，记录斜距、水平角和垂直角。

表1 角反射器移动方案mm

2.结果分析

将两种监测系统的原始数据进行处理，得到GB-Radar坐标系一维变形量ΔBg和测量机器人在GB-Radar坐标系下雷达视线向(B方向）形变量ΔBr，以及两种监测系统的中误差，利用文中所述数据配准和数据融合的数学模型，计算雷达视线向B方向的GB-Radar与测量机器人变形量的最小二估计值，结果见表2。

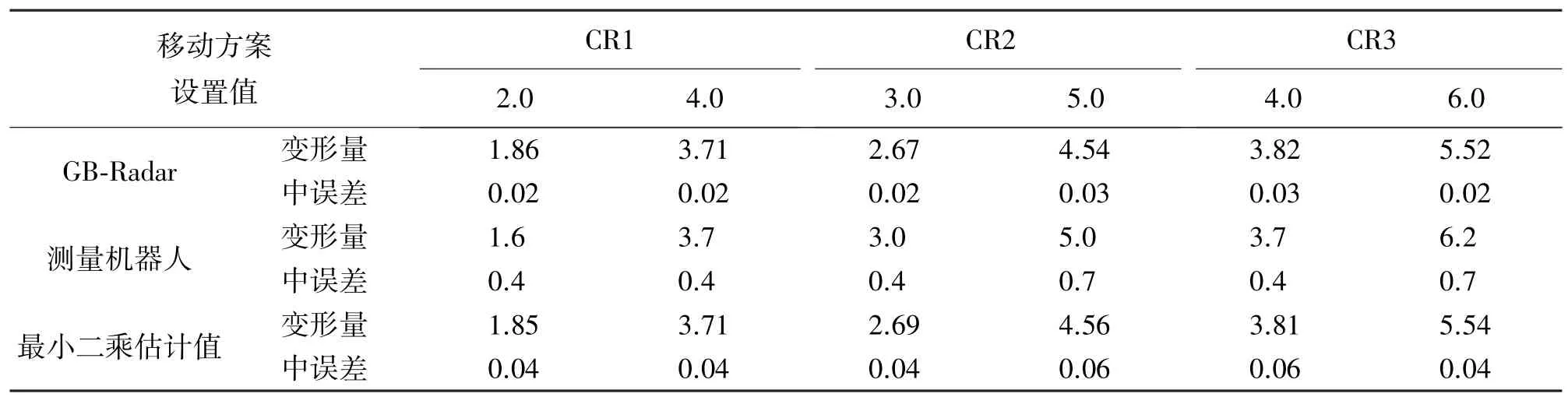
表2 两种监测数据在B方向的最小二乘估计值mm

表3 监测数据的融合结果mm

分析表2、表3可知，测量机器人空间变形量与设置值最大偏差为0.8 mm，变形监测精度优于1 mm。GB-Radar监测结果与设置值最大误差为0.48 mm，变形监测精度优于0.05 mm，GB-Radar监测精度高于测量机器人。由于GB-Radar雷达视线向监测精度较高，利用最小二乘估计的方法融合了GB-Radar和测量机器人的变形观测值，使监测点的三维变形量包含了两种监测数据的变形信息，误差明显下降，最大监测误差也由0.8 mm降为0.29 mm，监测精度由毫米级变为亚毫米级，提高了测量机器人的三维变形监测精度。

五、结束语

GB-Radar和测量机器人在监测技术上互为补充，两种技术的融合将突破单一监测技术的限制。本文通过分析GB-Radar和测量机器人两种监测系统模型的关系，建立了两种变形监测量数据配准和数据融合的数学模型。通过设计试验，利用两种监测仪器对可移动角反射器进行监测，试验表明，GBRadar用于变形监测的精度优于毫米级，高于测量机器人，融合了GB-Radar监测量和测量机器人三维变形量的监测点变形监测数据，使得最大监测误差从0.8 mm降为0.29 mm，监测精度达到了亚毫米级。

[1]张正禄.测量机器人[J].测绘通报，2001(5）：17.

[2]郭腾龙，岳建平.测量机器人ATR性能分析与测试[J].测绘通报，2012(8）：92-94.

[3]陈顺超，黄平明，孙胜江.测量机器人用于悬索桥静载试验的精度分析[J].广西大学学报：自然科学版，2011，36(1）：88-93.

[4]陈晨，马继国，王联升.测量机器人在工程监测中的应用[J].河北工程技术高等专科学校学报，2011(4）：62-65.

[5]黄其欢，张理想.基于GBInSAR技术的微变形监测系统及其在大坝变形监测中的应用[J].水利水电科技进展，2011，31(3）：84-87.

[6]于泓，彭军还.IBIS-M系统在露天矿边坡监测的应用[J].采矿技术，2011(4）：100-102.

[7]王鹏.地基SAR干涉测量原理及其形变监测应用研究[J].测绘信息与工程，2012，37(4）：22-25.

[8]IANNINI L，GUARNIERI A M.Atmospheric Phase Screen in Ground-based Radar：Statistics and Compensation[J]. IEEE Geoscience and Remote Sensing Letters，2011，8(3）：537-541.

[9]刁建鹏，梁光胜.地面雷达的位移监测试验研究[J].测绘科学，2011，36(2）：62-64.

[10]D’ARIA D，FERRETTI A，GUARNIERI A M，et al. SAR Calibration Aided by Permanent Scatterers[J].科学版，2012，37(10）：1173-1176.

[13]刁建鹏，梁光胜.地面雷达的位移监测试验研究[J].测绘科学，2011，36(2）：62-64.

[14]刁建鹏.微波干涉测量在高层建筑动态监测中的应用[J].振动与冲击，2010，29(11）：177-179，261.

[15]刁建鹏，黄声响.地面干涉雷达在建筑变形监测中的应用[J].测绘通报，2009(9）：45-47.

[16]DEI D，GRAZZINI G，LUZI G，et al.Non-Contact Detection of Breathing Using a Microwave Sensor[J].Sensors，2009(9）：2574-2585.

[17]许小剑，黄培康.雷达系统及其信息处理[M].北京：电子工业出版社，2010.

[18]CHERNOV N，LESORT C.Least Squares Fitting of Circles[J].Journal of Mathematical Imaging and Vision，2005，23(3）：239-252. IEEE Transactions on Geoscience and Remote Sensing，2010，48(4）：2076-2086.

[11]ROUYET L，KRISTENSEN L，DERRON M H，et al. Characterization of Large Instabilities Displacements Using Ground-Based InSAR[C]∥EGU General Assembly Conference Abstracts.Vienna：[s.n.]，2012.

[12]TAKAHASHI K，MATSUMOTO M，SATO M.Continuous Observation of Natural Disaster Affected Areas U-sing Ground-based SAR Interferometry[J].Applied Earth Observations and Remote Sensing，2013，6(3）：1-8.

Study on Data Fusion of GB-Radar and Georobot

YUE Jianping，ZENG Baoqing，GUO Tenglong，DONG Jie

分析Ground-based Radar(GB-Radar）与测量机器人变形监测技术的特点，以及两种监测技术数据融合所带来的优势。通过分析两种监测系统的关系，建立了这两种变形监测系统数据配准和数据融合的数学模型。通过设计试验，获取了GB-Radar与测量机器人对角反射器的变形监测数据。结果表明，对GB-Radar雷达视线向一维变形量与测量机器人三维变形量进行数据融合得到的监测点三维监测数据，最大监测误差明显降低，监测精度达到亚毫米级。

GB-Radar；测量机器人；变形监测；数据配准；数据融合

P258

B

0494-0911(2014）10-0033-03

2013-11-11

国家自然科学基金( 41174002；41304025）

岳建平(1963―），男，江苏溧阳人，教授，主要从事精密工程测量及变形监测的教学和研究工作。

岳建平，曾宝庆，郭腾龙，等.GB-Radar与测量机器人数据融合方法研究[J].测绘通报，2014(10）：33-35.

10.13474/j.cnki.11-2246.2014.0322