北斗三频组合在数据预处理中的应用

张晨晰，党亚民，王潜心，于志刚

(1.山东科技大学，山东青岛 266510；2.中国测绘科学研究院，北京 100083；3.中国矿业大学，江苏徐州 221116）

北斗三频组合在数据预处理中的应用

张晨晰1，2，党亚民2，王潜心3，于志刚1

(1.山东科技大学，山东青岛 266510；2.中国测绘科学研究院，北京 100083；3.中国矿业大学，江苏徐州 221116）

一、引 言

周跳的探测与修复和粗差的探测与剔除是卫星导航系统载波相位数据预处理工作的重要内容。传统的周跳探测方法有高次差法、多项式拟合法、电离层残差法等[1]。粗差探测与剔除的方法有滤波法和小波法等。随着多频GNSS的出现和发展，越来越多的学者研究利用多频观测数据进行周跳和粗差的探测与处理，并提出了一些有效的方法。文献[2―6]给出了利用多频数据探测和修复GPS周跳与粗差的几种组合，可以在单历元中有效探测周跳与粗差。

我国的北斗导航系统(BDS）已发射3个基准频率为2.046 MHz的频率信号：1 561.098 MHz、1 207.14 MHz和1 268.52 MHz。本文在介绍多频伪距/载相组合法探测周跳的原理的基础上，结合北斗三频载波相位组合的特性，给出了组合观测量的选取标准，分析了三频组合比双频组合的优势，并选取了3组组合作为探测周跳和粗差的检验量，通过实测三频数据的实例分析表明，该组合能探测出任何情况下的大于1周的周跳和大于0.2周的粗差。

二、多频伪距/载相组合法原理

观测方程的模糊度可用伪距和相位表示为

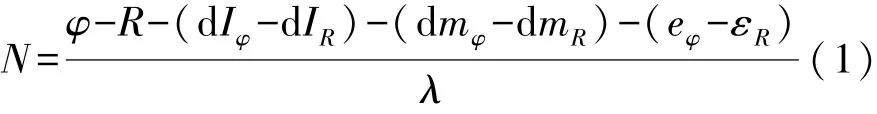
当历元间电离层延迟和多路径效应变化较小时，将式(1）在历元间相减，可以得到周跳的估值

若组合系数为(i，j，k），多频组合观测量的周跳估值为

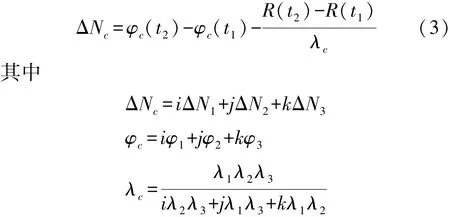
不难看出，当原始载波观测值三频上发生周跳ΔN1、ΔN2、ΔN3时，将在组合观测值中被放大为ΔNc。

以周为单位的载波观测噪声标准差σφ1＝σφ2＝σφ3＝σφ，伪距组合观测量噪声标准差为σR1＝σR2＝σR3＝σR，则应用误差传播定律根据式(3）可得周跳检测量ΔNc标准差为

σΔNc越小，通过直接取整获得正确周跳值的成功率越高[7]。

3种不同的频率组合(i1，j1，k1）、(i2，j2，k2）、(i3，j3，k3）探测出的周跳取整后分别为n1、n2、n3，则有

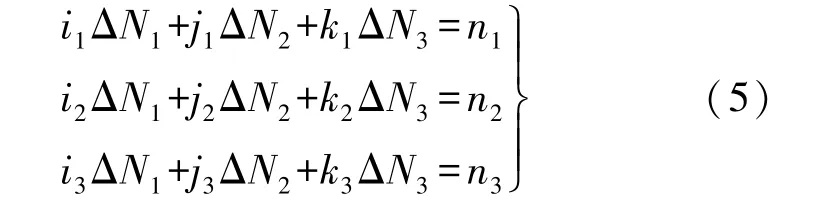
即可得到原始数据中各频率的周跳ΔN1、ΔN2、ΔN3。估计精度取决于电离层延迟和多路径效应在历元之间的变化，伪距和载波相位测量的观测噪声，以及载波波长λc的大小。

三、三频组合观测量的选取

1.组合观测量的选取标准

若不加限制，三频载波相位组合观测量可组成无穷组组合。通过对组合观测值的误差分析，组合后应保留模糊度的整周特性，具有适当的波长、较小的电离层折射误差影响和较小的观测噪声。为衡量不同组合的优劣，选择以下指标。

(1）波长参数αλ

波长参数定义为组合波长相对于基准波长的大小，可表示为

式中，λ0为基础频率2.046 MHz的波长值。

整数α取值越小，波长越大，即α可作为表征波长大小的参数。3种频率可以组合出适用于周跳探测的较长的波长。

(2）电离层影响参数q

在长基线相对定位中，电离层是影响载波相位模糊度正确固定的主要因素。电离层折射误差与频率大小有关。组合观测量的电离层影响因子可表示为

q越小表示电离层误差影响越小。

(3）观测噪声方差σφc

由于多路径效应误差与频率及观测环境有关，且不易被分离出来，很难对其进行定量分析，因此常把其与随机噪声放在一起加以考虑[1]。运用误差传播定律可得组合观测值以周为单位的观测噪声方差为

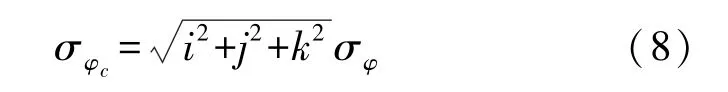
式中，σφ为以周为单位的各载波随机噪声。

由文献[8]的结论可知，载波相位组合存在着4个噪声最小的轴：S＝0、S＝1、S＝2、S＝-1(S为组合系数的和，即S＝i＋j＋k）。

(4）周跳检测量的标准差σΔNc

σΔNc的计算公式如式(4），据文献[7]的结论，三频伪距相位组合观测量的周跳检测量的标准差σΔNc小于0.15周，就能够以大于99.9%的成功率获得正确的相位组合观测量周跳值，且σΔNc越小，成功率越高。

对周跳和粗差探测而言，考虑到电离层和多路径在历元间的变化不稳定，最优组合的选取应该满足以下条件：

1）波长尽可能长；

2）电离层影响和噪声尽可能小；

3）周跳检测量的标准差最小。

取以周为单位的载波观测噪声标准差σφ＝0.01 cycle，伪距组合观测量噪声标准差σR＝0.3 m，根据上述标准选取出的几组组合的属性值见表1，并按σΔNc从小到大排列。为与双频组合作比较，表1最后两行为较好的双频组合的属性。

表1 组合观测值属性

由表1可以看出：

1）双频组合(1，-1）波长短且周跳检测量的标准差达到了0.5，大大降低了周跳探测的成功率；而(7，-9）组合波长较长但电离层影响大，而三频能获得更优的组合，因此三频比双频组合更具优势。

2）(4，-2，-3）组合虽然波长长，周跳检测量的标准差也较小，但电离层影响大，因此该组合不予采用。

2.不相关条件

对于组合观测量的选取，不仅要考虑波长和噪声等条件，所选的3组组合系数之间也需要满足一定的关系。式(4）可表示为

要求得周跳探测值[ΔN1ΔN2ΔN3]T的值，要求选取的三组组合必须是线性无关的，也就是组合系数矩阵A的秩R(A）应为3，即

在表1中列出的所有较优的组合中，如假设3组组合均选择了S＝0的组合，即i＋j＋k＝0，3组组合就是相关的，周跳探测值[ΔN1ΔN2ΔN3]T无解或有无穷多解，也就难以准确探测出所有的周跳值，即假设ΔN1＝ΔN2＝ΔN3＝x，那么不管x是大周跳，还是小周跳，该组组合都不能探测出来。

四、实例分析

根据以上分析综合考虑，选择波长尽可能长、电离层影响和噪声尽可能小，且3组组合线性无关的3个组合：(0，-1，1）、(-1，-5，6）、(-4，1，4）。由式(4）可以解得ΔN1、ΔN2、ΔN3。

本文选取2013年9月9日采样间隔为1 s的北斗三频原始观测数据，在76历元之后按以下条件人为地加入周跳。

1.小周跳的探测和修复

(1）单个频率加入小周跳的情况(L1:＋1 cycle）

如图1所示，组合(0，-1，1）没有周跳，组合(-1，-5，6）周跳值取整后为-1，组合(-4，1，4）周跳值取整后为-4，解得ΔN1＝1，ΔN2＝0，ΔN3＝0。

(2）两个频率上加小周跳的情况(L1:＋1 cycle，

L2:＋1 cycle）

如图2所示，组合(0，-1，1）周跳值取整后为-1，组合(-1，-5，6）周跳值取整后为-6，组合(-4，1，4）周跳值取整后为-3，解得：ΔN1＝1，ΔN2＝1，ΔN3＝0。

(3）3个频率上加小周跳的情况(L1:＋1 cycle，

L2:-1 cycle，L3:＋1 cycle）

如图3所示，组合(0，-1，1）周跳值取整后为2，组合(-1，-5，6）周跳值取整后为10，组合(-4，1，4）周跳值取整后为-1，解得：ΔN1＝1，ΔN2＝-1，ΔN3＝1。

其他试验表明：在载波相位中加入其他小周跳的试验结果也具备相同的探测效果，因篇幅限制，不再列举。

图1 小周跳探测(＋1，0，0）

图2 小周跳探测(＋1，＋1，0）

图3 小周跳探测(＋1，-1，＋1）

2.大周跳的探测和修复

(1）两个频率加入大周跳的情况

①L1：-1 cycle，L2：＋68 cycle

如图4所示，组合(0，-1，1）周跳值取整后为-68，组合(-1，-5，6）周跳值取整后为-339，组合(-4，1，4）周跳值取整后为72，解得：ΔN1＝-1，ΔN2＝68，ΔN3＝0。

图4 大周跳探测(-1，＋68，0）

②L1：＋68 cycle，L2：-100 cycle

如图5所示，组合(0，-1，1）周跳值取整后为100，组合(-1，-5，6）周跳值取整后为432，组合(-4，1，4）周跳值取整后为-372，解得：ΔN1＝68，ΔN2＝-100，ΔN3＝0。

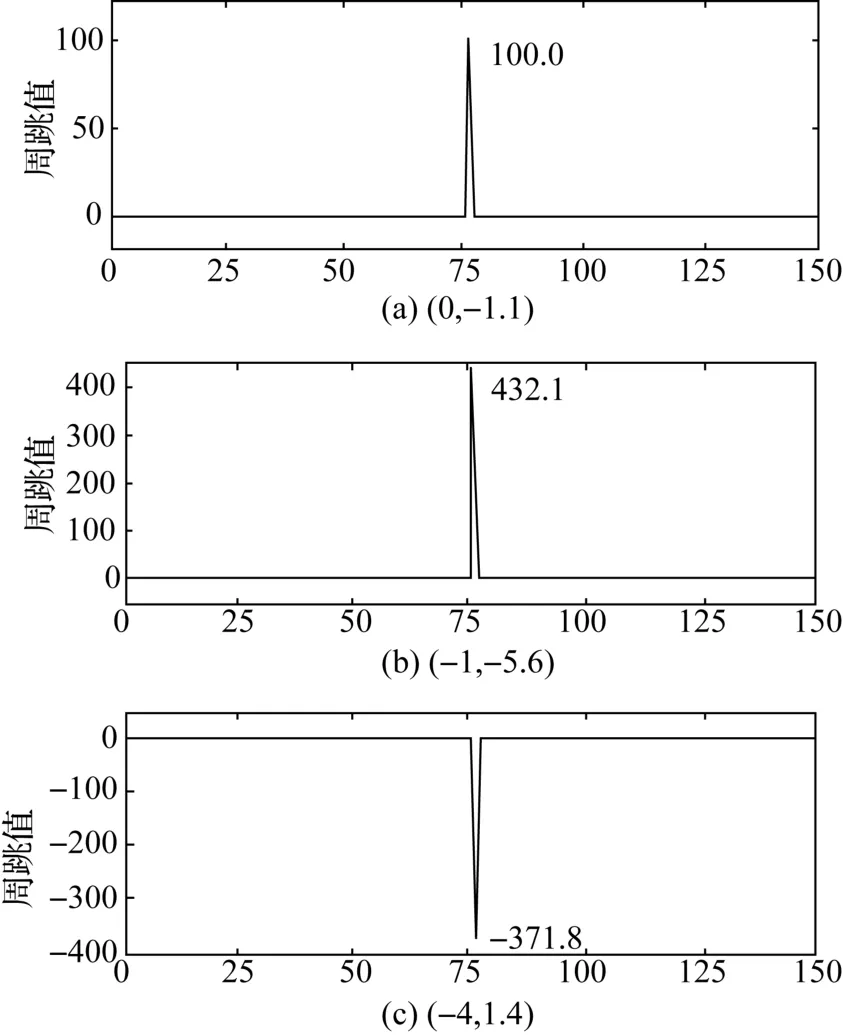
图5 大周跳探测(＋68，-100，0）

(2）3个频率均加入大周跳的情况

①L1：＋100 cycle，L2：-1 cycle，L3：＋68 cycle

如图6所示，组合(0，-1，1）周跳值取整后为69，组合(-1，-5，6）周跳值取整后为313，组合(-4，1，4）周跳值取整后为-129，解得：ΔN1＝100，ΔN2＝-1，ΔN3＝68。

图6 大周跳探测(＋100，-1，＋68）

②L1：-100 cycle，L2：-100 cycle，L3：-100 cycle

如图7所示，组合(0，-1，1）没有周跳，组合(-1，-5，6）没有周跳，组合(-4，1，4）周跳值取整后为-100，解得：ΔN1＝-100，ΔN2＝-100，ΔN3＝-100。

其他试验表明：在载波相位中加入其他大周跳的试验结果也具备相同的探测效果，因篇幅限制，不再列举。

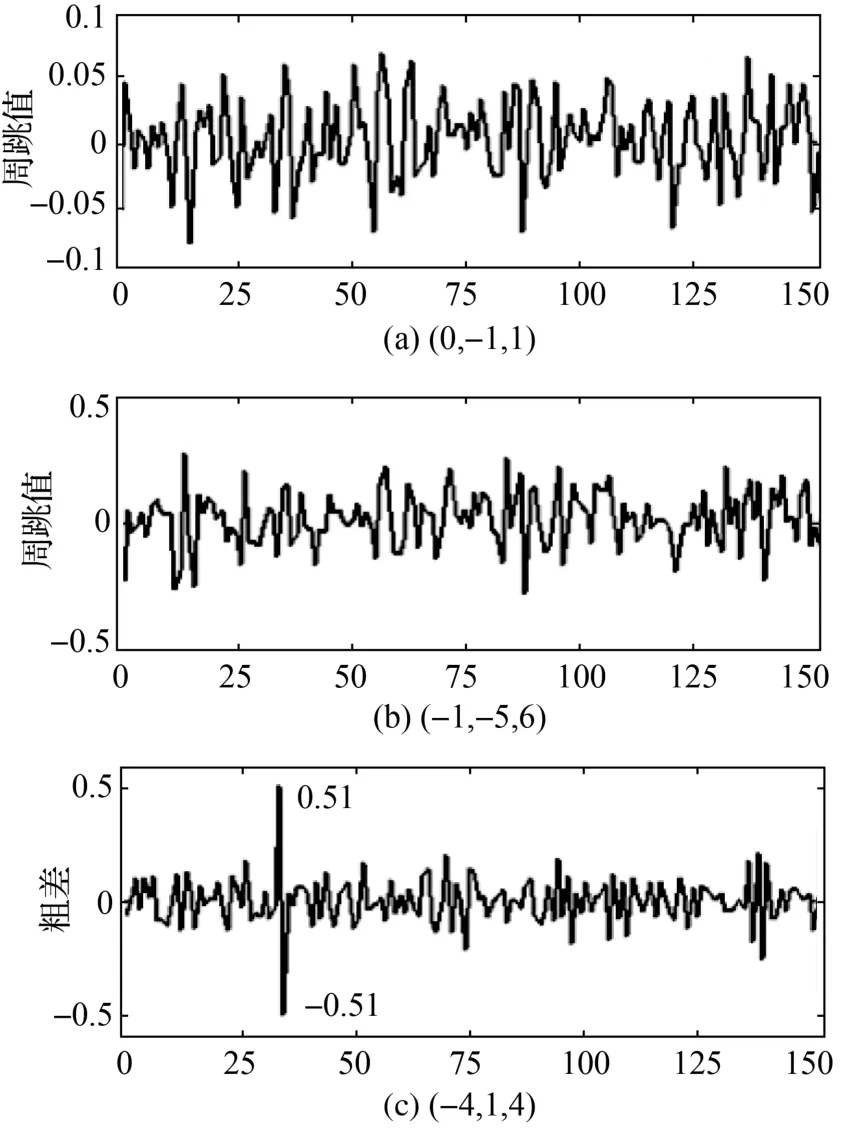
图7 大周跳探测(-100，-100，-100）

3.粗差的探测

对于粗差的探测，式(5）可改写为

式中，Ka(tb）中a为组合(ia、ja、ka）在tb时刻的粗差检测量值。本文在35历元按以下条件人为地加入半周和0.2周的粗差，以检测组合的粗差探测性能。

(1）单个频率加入半周粗差的情况(L1:＋0.5 cycle）

如图8所示，组合(0，-1，1）粗差检测量为(-0.49，0.50），组合(-1，-5，6）粗差检测量为(-2.46，2.54），组合(-4，1，4）粗差检测量为(0.51，-0.51），解得：Δ1＝0.21，Δ2＝-0.21，Δ3＝-0.19。

(2）多个频率加入0.2周粗差的情况(L1:＋0.2 cycle，L2:＋0.2 cycle，L3:-0.2 cycle）

如图9所示，组合(0，-1，1）粗差检测量为(-0.39，0.40），组合(-1，-5，6）粗差检测量为(-2.36，2.45），组合(-4，1，4）粗差检测量为(-1.39，1.39），解得：Δ1＝0.01，Δ2＝0.51，Δ3＝0.01。

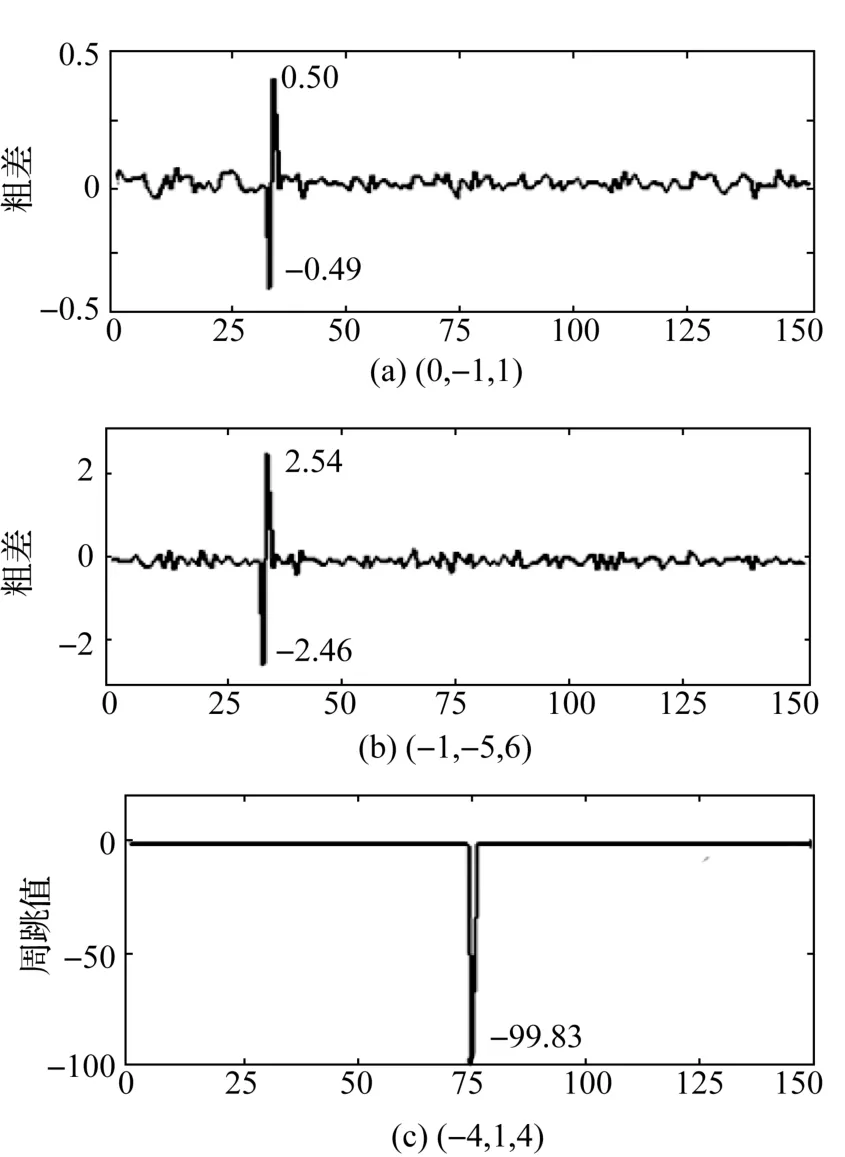
图8 粗差探测(0，＋0.5，0）

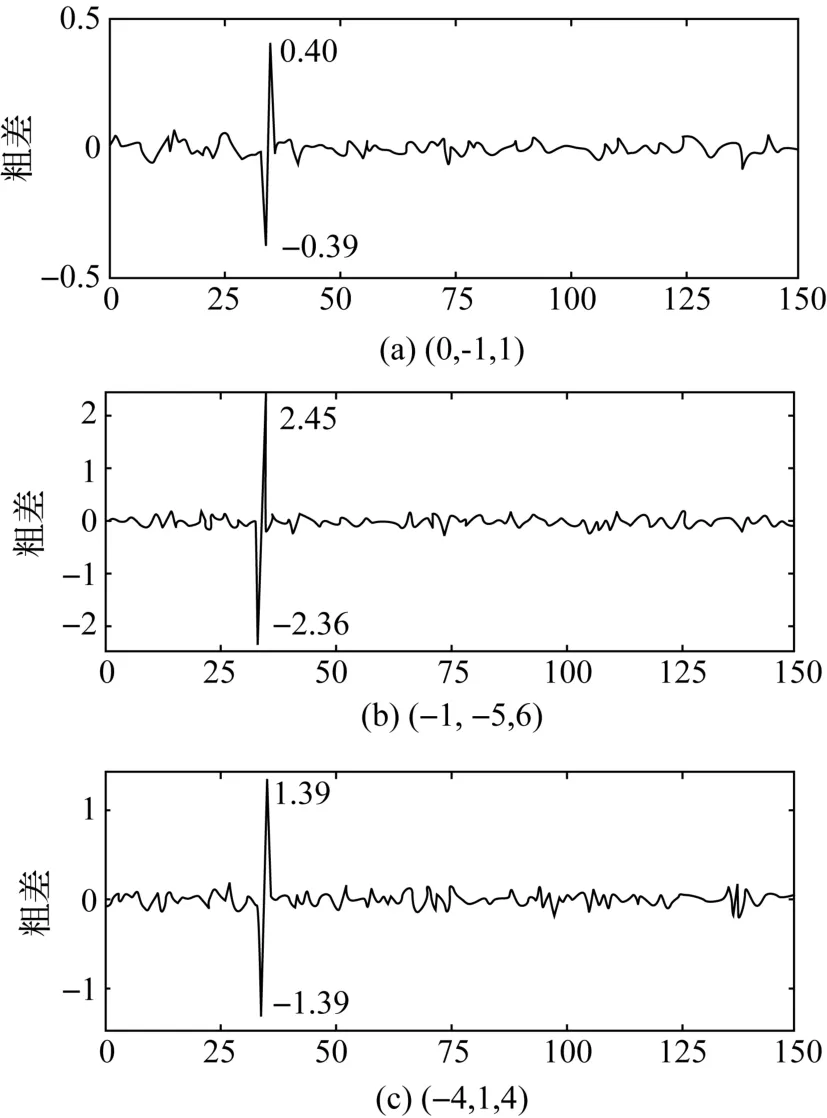
图9 粗差探测(＋0.2，＋0.2，-0.2）

五、结 论

1）探测周跳和粗差的组合观测值的选取需在周跳检测量的标准差最小的前提下，选取长波长、小电离层影响和小噪声的组合，还要求满足3组组合线性无关的条件，才能成功探测出所有情况下的周跳值。

2）由多频组合的属性分析表明，三频组合比双频组合更具优势。

3）北斗实测数据试验表明，组合(0，-1，1）、(-1，-5，6）、(-4，1，4）可以探测出北斗系统1周以上的所有周跳，是性能良好的探测周跳组合。

4）北斗实测数据试验表明，组合(0，-1，1）、(-1，-5，6）、(-4，1，4）可以探测出北斗系统0.2周以上的粗差，是性能良好的探测粗差组合。

[1]刘基余.GPS卫星导航定位原理与方法[M].2版.北京：科学出版社，2003.

[2]伍岳.第二代导航卫星系统多频数据处理理论及应用[D].武汉：武汉大学，2005.

[3]刘旭春，伍岳，黄学斌，等.多频组合数据在原始载波观测值预处理中的应用[J].测绘通报，2007(2）：14-17.

[4]王帅，高井祥.利用三频组合观测值进行GPS周跳探测与修复[J].测绘科学，2012，37(5）：40-42.

[5]范建军，王飞雪，郭桂蓉.GPS三频非差观测数据周跳的自动探测与改正研究[J].测绘科学，2006，31(5）：24-26.

[6]熊伟，伍岳，孙振冰，等.多频数据组合在周跳探测和修复上的应用[J].武汉大学学报：信息科学版，2007，32(4）：319-322.

[7]李金龙.GNSS三频精密定位数据处理方法研究[D].郑州：信息工程大学，2011.

[8]于兴旺.多频GNSS精密定位理论与方法研究[D].武汉：武汉大学，2011.

[9]孙保琪，欧吉坤，盛传贞，等.一种适于Compass周跳探测的三频数据优化组合[J].武汉大学学报：信息科学版，2010，35(10）：1157-1160.

[10]黄令勇，宋力杰，王琰，等.北斗三频无几何相位组合周跳探测与修复[J].测绘学报，2012，41(5）：763-768.

The Application of Multi-frequency Combination Observation in BDS Data Preprocessing

ZHANG Chenxi，DANG Yamin，WANG Qianxin，YU Zhigang

在介绍多频伪距/载相组合法进行数据预处理的原理基础上，结合北斗三频载波相位组合的特性，给出组合观测量的选取标准，分析三频组合相比双频组合的优势，并选取3组组合作为探测周跳和粗差的检验量。通过数据实例分析，该组合能探测出任何情况下大于1周的周跳和大于0.2周的粗差。

北斗；三频组合；周跳；粗差

P228.4

B

0494-0911(2014）10-0001-06

2013-12-10

国家自然科学基金(41404033）；国家863计划(2013AA122501）；中国博士后科学基金(2013M532135）；中国测绘科学研究院基本科研费(7771401）

张晨晰(1983―），女，山东泰安人，博士生，主要研究方向为GNSS组合定位。

张晨晰，党亚民，王潜心，等.北斗三频组合在数据预处理中的应用[J].测绘通报，2014(10）：1-6.

10.13474/j.cnki.11-2246.2014. 0315