改进的时延丢包网络控制系统的分析和控制

屈百达，陈龙，徐保国

江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122

改进的时延丢包网络控制系统的分析和控制

屈百达，陈龙，徐保国

江南大学轻工过程先进控制教育部重点实验室，江苏无锡 214122

1 引言

在传统点对点控制模式下，成本较高、布线复杂、信息封闭等一系列缺点日益突出。网络控制系统（Networked Control Systems，NCSs）的出现，适应了控制系统逐渐向网络化、分布化和智能化方向发展的趋势[1-2]。NCSs具有总体成本较低、故障诊断容易、高效率、高可靠性等优点。但是各节点在通过网络进行数据交换时，不可避免地出现网络诱导时延、数据丢包等非理想网络状况。网络诱导时延可能是定常、时变或是随机的。同时，网络时延也会因为不同的调度策略和网络故障等因素而发生变化。另一方面，数据包在传输过程中，如果存在连接中断或是网络阻塞，有可能导致数据包的丢失。网络时延和数据丢包的存在会降低整个NCSs的性能，甚至引起系统的不稳定[3-6]。因此，设计一个合理的控制器来保证NCSs在时延和丢包问题下的稳定性是很有必要的。这是NCSs的重要研究内容之一。

近年来，利用时滞系统理论的时滞相关条件对NCSs进行分析和设计得到学者广泛的关注[7-11]。文献[7]采用了模型变换方法，研究了时滞NCSs的稳定性。然而，模型变换方法需要对交叉项进行界定，具有一定的局限性。文献[8]将网络时延和丢包问题表述为具有时延界的NCSs综合模型，通过引入松弛变量，研究了NCSs的无记忆反馈控制器设计，但是证明中忽略了一些有用项，不可避免地带来了保守性。文献[9]采用积分不等式方法，提出了一种新的NCSs的H∞稳定准则，降低了模型变换和松弛变量带来的保守性，然而，中间的一些有效项仍然被丢弃。文献[10]运用自由权矩阵和函数的凸性，研究了具有时变或随机时延的NCSs的H∞反馈控制器设计问题，但由于引入了太多自由变量，大大地增加了计算量。

针对以上文献的不足，本文参考了文献[8]的模型，引入了具有逻辑判断功能的零阶保持器，对NCSs建立网络闭环时滞系统模型，充分考虑网络时延和数据丢包的问题。为了分析NCSs稳定性，将时滞区间分成两个不同的子区间，采用了包含网络时延上下界的分段Lyapunov-Krasovskii泛函，基于一个更紧的有限和不等式，得到了具有较少变量的稳定性条件。此外，本文通过采用改进的锥补线性化迭代方法，给出了一种保守性更小的状态反馈控制器的求解算法。

2 问题描述

考虑如下的线性系统：

其中，x(t)∈Rn，u(t)∈Rm分别为状态向量和控制输入向量，A，B为具有适当维数的常数矩阵。

为了便于系统的描述，给出如下合理的假设：

假设1 NCSs的传感器是时间驱动的，控制器和执行器是事件驱动的，数据采用单包传输。

假设2网络的实际输入u(t)是一个分段连续函数，可通过具有逻辑判断功能零阶保持器来实现。

假设3控制器和执行器总是选择最新到达的控制数据包而丢弃旧的数据包，当一个旧的数据包到达时，会被当作一个丢失的数据包来处理。

基于以上的假设，并考虑网络延迟、数据包丢失等不确定网络状况影响，采用文献[8]的建模方法，则控制系统可以描述为：

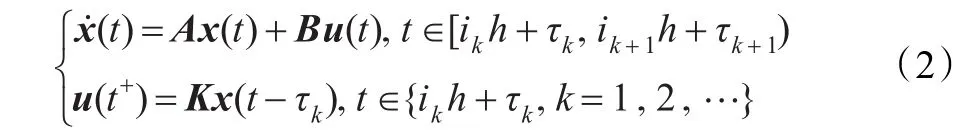
其中h为采样周期ik+1h+τk+1之间变化的时刻，即相应控制信号作用在系统（1）上的时刻；ik(k=1,2,…)是一些整数且{ik,k=1,2,…}⊆{0,1,…}；τk为网络诱导时延。

假设全部状态变量都是可测量的，因此式（2）可以改写为如下闭环采样系统：

注2由于采用零阶保持器，实现了执行器选择新到达的数据包而丢弃旧数据包的策略。所以假设ik+1＞ik总是成立，当ik+1=ik+1，表示传输中没有数据丢包，当α=ik+1-ik＞1，表示传输中有数据丢包，且丢包数为α-1。

借助文献[12]的思想将采样控制输入转化为输入时滞，式（3）可转化为闭环时滞系统。

基于式（4）～（6）的定义，则式（3）可改写为：

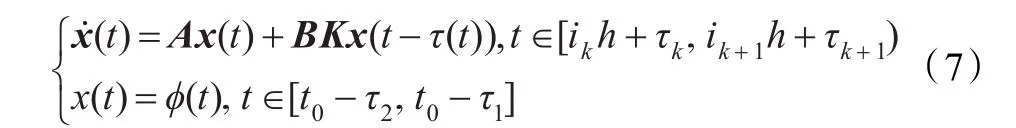
式（7）中，ϕ(t)为系统的初始函数。

文中定理证明将用到如下引理：

更进一步，下面式（10）成立的充分条件是式（11）成立：

可以得到式（10），证毕。

注3引理2可以看作文献[14]中引理1的连续形式，它在证明推导中起到了重要的作用。

注4式（9）的有限和不等式未运用任何自由矩阵，变量个数较少，具有较低的保守性和较高的求解效率，虽然式（10）中的ε1和ε2是时变的，不能直接利用MATLAB中的LMI工具箱求解，但是式（11）解决了这一问题，它可以直接利用LMI求解。

3 主要结论

本章考虑系统（7），并定义τa=(τ1+τ2)/2，给出系统（7）渐进稳定的充分条件并设计相应的状态反馈控制器。

3.1 NCSs稳定性分析

定理1对于给定标量τ2≥τ1≥0，矩阵K，假如存在具有适当维数的对称正定矩阵P＞0，Qi＞0(i=1,2,3)，Zi＞0(i=1,2,3)，满足以下LMI：

那么系统（7）是渐近稳定的。

注5*是由矩阵对称性得到的矩阵块。

证明：构造如下的Lyapunov-Krasovskii泛函

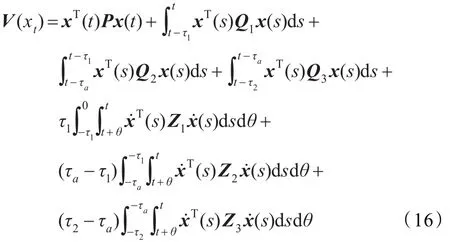
对V(xt)沿着系统（7）的轨线求导，可得：

情形2当τa≤τ(t)≤τ2，构造式（16）的Lyapunov-Krasovskii泛函并对V(xt)求导得到式（17），继续利用引理1和引理2来处理式（18）～（20）代入式（17），可得

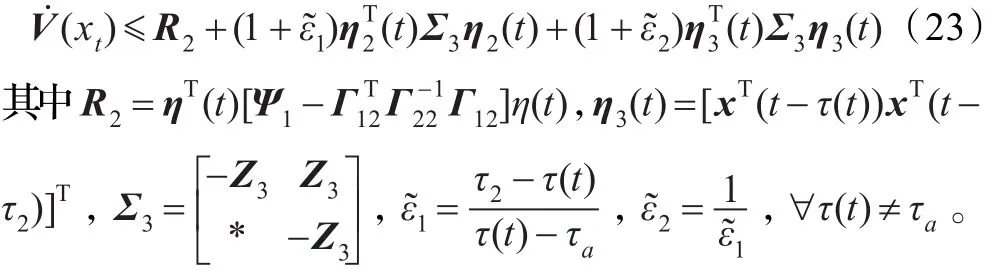
情形2的证明过程与情形1的类似，式（15）也保证了式（23）的(xt)＜0。因此式（14）和式（15）保证了τ1≤τ(t)≤τ2的时候，(xt)＜0，根据Lyapunov稳定性理论，系统式（7）是渐近稳定的。

注6在Lyapunov-Krasovskii泛函设计中，充分考虑了时延上下界的关系，在证明过程中，既没有运用模型变换也没有引入自由矩阵，只是有效地利用了有限和不等式进行处理。另外，证明中没有忽略任何有用项且具有较少的变量。相比较于文献[9，11]，定理1具有较小的保守性和计算量。在随后的实例中将加以说明。

3.2 NCSs控制器设计

那么系统（7）是渐近稳定的且控制器增益为K=YX-1。

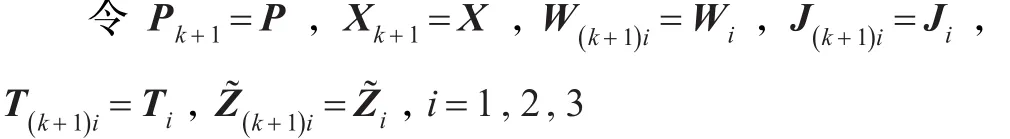
步骤4对于步骤3所得的K=YX-1，如果不等式（24）和（25）有可行解，则令τmax=τ2，适当的增加τ2并返回步骤2；如果步骤3所得的K=YX-1使得不等式（24）和（25）没有可行解，且k大于最大的迭代次数，则退出程序。否则，令k=k+1，返回步骤3。

4 仿真实例

例1考虑具有如下参数的系统

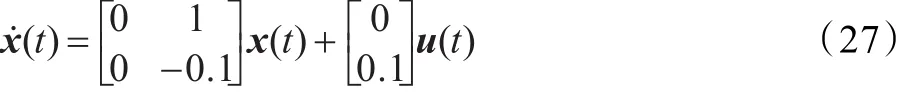
若给定控制器K=[-3.75-11.5]，利用定理1和LMI工具箱可以求得在不同下界τ1时的最大允许网络时延τ2，如表1所示，本文与相关文献比较结果具有较少的保守性和矩阵变量。

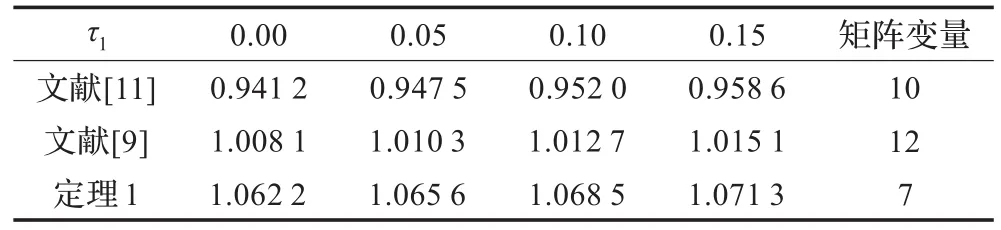
表1 不同下界τ1下最大允许网络时延的比较

对给定初始状态x0=[2,-1.5]T，控制器K=[-3.75-11.5]和求得的τ2=1.062 2，得到系统状态响应如图1所示，可看出系统是渐进稳定的。

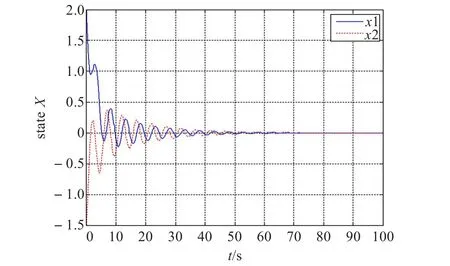
图1 τ2=1.062 2的系统状态响应

例2考虑具有如下参数的系统[8]

给定下界τ1=0，利用文献[8]的算法得到网络时延上界τ2=0.97。利用文献[15]的算法得到网络时延上界τ2=0.996，其中文献[15]经313次迭代得到控制器K=[-1.005 0-1.004 9]，而应用本文改进的锥补线性化迭代算法，在τ2=0.998时，系统仍然是稳定的，经98次迭代得到控制器K=[-1.041   9-1.041 4]。

本文改进的锥补线性化迭代算法相比于文献[15]的算法区别在于：文献[15]算法的终止条件是相当严格的，需要同时满足多个LMI的成立，造成迭代时间很长，而本文算法的终止条件只需满足式（24）～（25），所以终止条件更加宽松，与文献[15]的算法相比减少了迭代次数，减少了大量的计算时间。

假设初始状态x0=[2,-1.5]T，h=0.02 s，存在连续丢包数α-1∈[0,40]，在本节所获得的控制器K和最大允许时延上界τ2下，所考虑的系统状态响应如图2所示。由图可见，闭环NCSs是渐进稳定的。

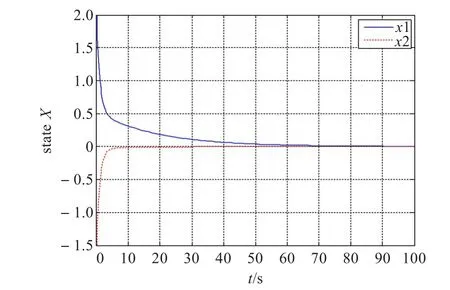
图2 系统状态响应

5 结束语

本文研究了一种同时包含有界时延和数据丢包问题的时变时滞网络控制系统，为了得到稳定性判据，一个分段Lyapunov-Krasovskii泛函和改进的有限和不等式方法被利用，有效地减少了结果的保守性和计算量，提高了求解效率，仿真结果表明，在闭环系统渐进稳定的条件下得到了最大允许时延上界，并在此基础上提出了一种改进的锥补线性化迭代算法求解反馈控制器，算例仿真表明了该算法的有效性和先进性。值得注意的是，目前大多数的研究主要针对线性的网络控制系统，下一步主要工作是研究非线性的网络控制系统的建模与控制问题。

[1]Yang T C.Networked control system：a brief survey[J]. IEE Proceedings-Control Theory and Applications，2006，153（4）：403-412.

[2]Gupta R A，Chow M Y.Networked control system：overview and research trends[J].IEEE Transactions on Industrial Electronics，2010，57（7）：2527-2535.

[3]Zeng Hongbing，He Yong，Wu Min，et al.Absolute stability and stabilization for Lurie networked control systems[J]. International Journal of Robust and Nonlinear Control，2011，21（14）：1667-1676.

[4]LinChong，WangZidong，YangFuwen.Observ-erbased networked control for continuous-time systems with random sensor delays[J].Automatic，2009，45（2）：578-584.

[5]孙业国.时延丢包网络控制系统的分析与控制[J].计算机工程与应用，2012，48（21）：89-93.

[6]Li H，Chow M Y，Sun Z.State feedback stabilisation of networkedcontrolsystems[J].IETControlTheoryand Applications，2009，3（7）：929-940.

[7]Kim D S，Lee Y S，Kwon W H，et al.Maximum allowable delay bounds of networked control systems[J].Control Engineering Practice，2003，11（11）：1301-1313.

[8]Dong Yue，Han Qinglong，Chen Peng.State feedback controllerDesignofnetworkedcontrolsystems[J].IEEE Transactions on Circuits and Systems II：Express Briefs，2004，51（11）：640-644.

[9]Jiang Xiefu，Han Qinglong，Liu Shirong，et al.A new hinfinity stabilization criterion for networked control systems[J].IEEE Transactions on Automatic Control，2008，53（4）：1025-1032.

[10]Tian Engang，Yue Dong.A new state feedback H-infinity control of networked control systems with time-varying network conditions[J].Journal of the Franklin Institute，2012，349（3）：891-914.

[11]Jiang Xiefu，Han Qinglong.Delay-dependent robust stability for uncertain linear systems with interval time-varying delay[J].Automatica，2006，42（6）：1059-1065.

[12]Fridman E，Shaked U，Suplin V.Input/output delay approach torobustsampled-dataH-infinitycontrol[J].Systems and Control Letters，2005，54（3）：271-282.

[13]Han Qinglong.Absolute stability of time-delay systems withsector-boundednonlinearity[J].Automatica，2005，41（12）：2171-2176.

[14]Peng Chen.Improved delay-dependent stabilisation criteria for discrete systems with a new finite sum inequality[J]. IET Control Theory and Applications，2012，6（3）：448-453.

[15]He Yong，Liu Guoping，Rees D，et al.Improved Stabilisationmethodfornetworkedcontrolsystems[J].IET Control Theory and Applications，2007，1（6）：1580-1585.

QU Baida,CHEN Long,XU Baoguo

Key Laboratory of Advanced Process Control for Light Industry Ministry of Education,Jiangnan University,Wuxi,Jiangsu 214122,China

This paper is concerned with the problem of the stability analysis and controller design for networked control systems（NCSs）with bounded,time-varying network delays and data dropout by modeling the time-varying delay systems. Construct a new Lyapunov-Krasovskii functional and make full use of the information on the upper and lower bounds of the delay.A tighter finite sum inequality is presented to deal with delay interval.A less conservative stability criteria is derived.The state feedback controller design is obtained with an improved cone complementarity linearization algorithm. Since neither model transformation nor free-weighting matrices is employed in the derivation of these results,the proposed approach will reduce calculation.Numerical examples are given to illustract the effectiveness of the proposed method.

Networked Control Systems（NCSs）;finite sum inequality;Linear Matrix Inequality（LMI）;cone complementarity linearization algorithm

将网络控制系统建模为时变时滞系统模型，考虑有界、时变时延和丢包的网络控制系统的稳定性分析和控制器设计问题。首先构造一个新的分段Lyapunov-Krasovskii泛函，充分利用时延上下界信息，然后结合更紧的有限和不等式处理时滞区间，得到具有较小保守性的稳定性准则，基于一种改进的锥补线性化迭代算法给出状态反馈器设计方法，证明中没有引进模型变换和自由矩阵，减少了计算上的复杂性。通过实例表明上述方法的有效性。

网络控制系统；有限和不等式；线性矩阵不等式；锥补线性化迭代算法

A

TP273

10.3778/j.issn.1002-8331.1212-0325

QU Baida,CHEN Long,XU Baoguo.Improved analysis and control for networked control systems with network-induced delay and data dropout.Computer Engineering and Applications,2014,50（22）：130-135.

国家自然科学基金（No.30971689）；高等学校学科创新引智计划资助（No.B12018）；江苏省产学研联合创新资金项目（No.120767）。

屈百达（1956—），男，教授，博导，主要研究方向：时滞系统，鲁棒控制，模式识别与数据处理；陈龙（1988—），男，硕士研究生，主要研究方向：网络控制系统，鲁棒控制；徐保国（1950—），男，教授，博导，主要研究方向：过程控制与优化，无线传感网络。E-mail：chenlongc428@163.com

2012-12-27

2013-04-07

1002-8331（2014）22-0130-06

CNKI网络优先出版：2013-04-18,http://www.cnki.net/kcms/detail/11.2127.TP.20130418.1618.020.html