半监督免疫克隆选择图划分方法

刘汉强

陕西师范大学计算机科学学院，西安 710119

半监督免疫克隆选择图划分方法

刘汉强

陕西师范大学计算机科学学院，西安 710119

LIU Hanqiang.Semisupervised immune clone selection graph partition algorithm.Computer Engineering and Applications,2014,50（22）：11-16.

1 引言

对聚类方法的研究一直是模式识别领域一个比较活跃而且极负挑战性的研究方向。聚类算法可分为无监督和半监督聚类，前者在聚类过程中，不利用任何先验信息；后者利用少量的先验信息来引导聚类过程，在一定程度上可以克服无监督聚类的盲目性，提高了聚类算法的性能。

近几年来，利用图谱划分理论来解决聚类问题成为一个新的研究热点。图谱划分是一类基于两点间相似关系的方法[1]，并通过最大化或最小化某一图谱划分准则获得样本的划分结果。由于图谱划分准则的优化问题是一个NP难的问题，为此许多近似求解图谱划分的方法被提出。谱聚类[2-4]是一种常见的解决图谱划分的方法，它利用数据的Laplacian矩阵的特征向量进行聚类，获得聚类准则在放松了的连续域中的全局最优解。此外，采用遗传算法或免疫算法等自然计算的方法来求解图谱划分问题，也是一种新的研究思路。该类方法把图谱划分准则作为目标函数进行优化，因此不需要求解相似性矩阵的特征向量来实现图谱划分。

在聚类过程中利用一定量先验信息会显著提高聚类算法的性能。半监督学习中的先验信息主要有两种，一是以样本点成对限制形式出现的监督信息，二是样本的类属信息。对于用户来说要确定样本类属会比较困难，而获得一些关于样本点是否可以或不能位于同一类的限制信息将会比较容易。另外，基于限制的先验信息比类属信息更一般，可以从类属信息获得等价的成对限制信息，反之则不然。由于图谱划分方法是基于两点间相似关系的方法，这使得利用成对限制先验信息变得非常容易。为此，本文提出一种半监督的免疫克隆选择图划分方法，首先将成对限制信息和最短路径距离测度引入到图谱划分方法样本点的相似性测度中，使得构造的相似性矩阵一方面充分体现了数据的全局一致性，另一方面实现了成对限制信息在样本空间的有效传播，然后在获得的相应的相似性矩阵的基础上，利用免疫克隆选择优化方法[5-6]来优化图谱划分准则，此外，在进化过程中利用权核k均值算法的目标函数和图谱划分准则的等价性[7]，提出了一个个体修正算子，使得个体以更快的速度向更优的方向进化。在USPS手写体数字集和UMIST人脸数据集的仿真实验验证了方法的鲁棒性和有效性。

2 谱图划分理论与免疫克隆选择优化

2.1 谱图划分理论

已知给定的任意特征空间中的数据集合X= {x1,x2,…,xn}，传统的图划分方法将这些数据表示成一个带权无向图G=(V,E,S)，其中结点vi∈V对应着特征空间中的数据点xi，eij∈E表示连接两个结点vi和vj的边，边的权值为Sij，即为数据点xi和xj的相似性值，因此S为数据间的相似性矩阵。在构造的图的基础上，通过优化某种谱图划分准则来对该图进行划分，获得这些数据的聚类结果，也就是将数据的聚类问题转化为在图G上的图划分问题。在图G上的划分就是将图G= (V,E,S)划分为k个互不相交的子集C1,C2,…,Ck，划分后保证每个子集Cl(1≤l≤k)内数据点间的相似性大，不同的子集Cp和Cq(1≤p≤k,1≤q≤k,p≠q)之间数据点间的相似性小。常见的划分准则[2，3，8-10]有最小切准则、率切准则、规范切准则、最小最大切准则等，划分准则的好坏直接影响到聚类结果的质量。

在谱图划分理论中，将图G划分成C1和C2两个互不相交的子图的目标函数定义为两个子图之间的切(Cut)，其具体形式如下：

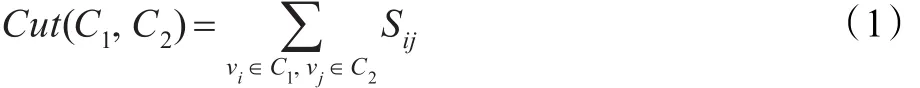
2000年，Shi和Malik提出了规范切（Normalized Cut，NCut）准则[2]，该准则的目标函数为：

其中，degree(C1)=Cut(C1,G)表示子图C1中的结点到图G中所有结点的权值之和。当需要对图进行多类划分时，可以采用多路谱图划分准则。下式为多路规范切（Multiway Normalized Cut，MNCut）准则[2，10]的定义：

规范切准则通过引入容量的概念来规范化类间相关性，从而不仅能够衡量样本集类间的相似程度，也能衡量类内数据间的相似程度。较好地解决了已有准则将少数样本点孤立为一类的偏斜划分问题。

2.2 免疫克隆选择优化方法

对于图划分问题而言，求解图谱划分准则是一个NP难的问题[2]。传统的优化算法由于本身存在一些局限性和不足，已经很难达到这种复杂问题的优化求解要求。作为一种新的全局优化搜索算法，免疫克隆选择算法[5]在算法实现上兼顾全局搜索和局部搜索，它模拟了生物学抗体克隆选择过程中的学习、记忆、抗体多样性等特性，并利用相应的算子保证了该算法能快速地收敛到全局最优解，至今该算法已在模式识别、数据挖掘和组合优化等领域得到了广泛的应用[5-6，11-12]。

免疫克隆优化算法的基本流程如下：

步骤1初始化抗体种群A(k)，k=0，初始化算法参数，计算初始种群种个体的亲和度。

步骤2依据亲和度和设定的抗体克隆规模，对抗体种群A(k)依据克隆比例进行克隆操作，得到克隆后的种群Y(k)。

步骤3以概率pm对Y(k)实现免疫基因操作，得到新的抗体种群Z(k)。

步骤4对Z(k)进行克隆选择操作，得到新的抗体种群A′(k)。

步骤5若满足终止条件，输出A′(k)，否则A(k+1)=A′(k)，k=k+1，返回步骤2。

克隆操作有效地实现了搜索空间的扩张；免疫基因操作实现了抗体亲和度的成熟和多样性的产生[5]；克隆选择操作通过局部择优，有效地压缩了种群的大小。

3 半监督免疫克隆选择优图划分算法

为了解决谱图划分准则的优化问题，引入成对限制信息和最短路径距离来构造相似性矩阵，并采用免疫克隆选择算法来优化图谱划分准则，提出了半监督免疫克隆选择图划分方法。

3.1 融合成对限制信息的最短路径距离相似性测度

把谱图划分理论用于数据聚类前的首要工作是构造相似性矩阵，相似性矩阵中的每一个元素表示的是两个数据点之间相似性。由前面介绍的谱图划分理论可知，数据集中的样本点可以看做是图G中结点，因此样本点间的相似性可以采用结点间的距离来衡量。此外，为了在分类问题中既考虑已有的半监督信息（成对限制信息），又充分考虑数据的全局一致和局部一致性，在本文中，引入融合成对限制信息的最短路径距离测定来构造样本间的相似性。设X={x1,x2,…,xn}是特征或数据点的集合，两个样本点xi和xj之间的最短路径距离具体定义如下：

其中，Pij表示连接数据点xi和xj的所有路径的集合，p表示该路径集合中的任意一条路径，len为该路径的长度，ph表示该路径上的第h个结点。L(ph,ph+1)为连接路径上相邻两点间的距离，其定义如下：

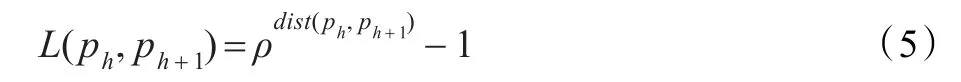
其中，dist(ph,ph+1)为ph与ph+1之间的欧氏距离，ρ＞1为伸缩因子。为了有效地利用成对限制信息，采用mustlink和cannot-link这两种类型的成对点限制来辅助样本点间的距离的计算，其中，must-link限制规定两个样本必须在同一聚类中，cannot-link限制规定两个样本不能在同一聚类中。具体来说，就是对式（5）中的两点之间的欧式距离dist(xi,xj)施加成对限制信息。如果(xi,xj)∈must-link，则dist(xi,xj)=0；如果(xi,xj)∈cannot-link，则dist(xi,xj)=inf。

显然，采用了成对限制信息的最短路径距离测度仍然满足距离度量的三个条件，即对于结点xi，xj和xk：

这种距离测度可以度量沿着流形上的最短路径，使得位于同一流形上的两点可以用许多较短的边相连接，而位于不同流形上的两点要用较长的边相连接，从而实现了放大位于不同流形上的数据点间的距离，而缩短位于同一流形上的数据点间的距离的目的。因此，在此距离测度的基础上定义样本点间的相似性度量：

3.2 半监督免疫克隆选择图划分方法

根据3.1部分定义的相似性测度，可以得到对应的无向图G，下面利用免疫克隆选择优化方法对该图进行划分得到划分结果。

3.2.1 亲和度函数

为了方便起见，且不失一般性，本文仅以规范切准则为例介绍半监督免疫克隆选择图划分算法，关于其他准则的半监督免疫克隆选择图划分框架可以类似得到。对多路规范切准则进行化简，其公式可以进一步表示为：

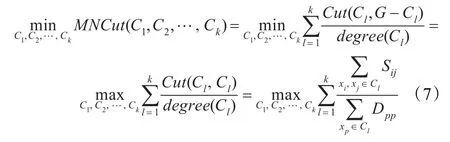
因此，多路规范切准则的最小化问题转化为了最大化问题，其中D为度矩阵，其对角元素Dpp是相似性矩阵S的第p行的元素之和，其余元素为零。根据公式（7）给定的多路规范切准则的等价形式，将公式（7）作为半监督免疫克隆选择图划分的亲和度函数。

3.2.2 编码及免疫算子设计

由谱图划分准则可知，划分的目标是获得数据集X的k个划分。这里将每个数据点的类别作为优化求得的解，认为数据集的一个划分结果就是一个抗体，每个抗体中的基因位是由该数据点的归属类别确定，抗体的编码长度为数据集中数据点的数目。已知数据集的规模为n，聚类的类别数为k，因此种群中第i个抗体ai的编码方式为：

基于免疫克隆选择优化的图划分方法中主要包括克隆、变异和选择三个操作算子。在这些算子的作用下，使得群体不仅能够维持多样性，防止“早熟收敛”，并且还能迅速地向可行解方向进化。

假设种群的规模为N。抗体的克隆操作就是在适应度最高的抗体中选择m个抗体进行克隆，克隆规模是Nc。传统的进化算法一般保持种群规模不变，强调了自然选择中的个体竞争。而克隆操作通过最优抗体复制使得对该抗体同时进行多种操作提供了可能。

抗体的变异操作是为了产生具有多样性的抗体，从而得到问题的全局最优解。变异操作就是产生1到n之间的一个随机整数，然后对其对应的基因的位置进行变异。由于每个基因位对应于该数据点的类别，因此产生一个0和1之间的随机数，如果该随机数小于变异概率，则该基因位就被变异为1到k之间的任意整数，且该整数不能和原来基因位上的数相同。

对抗体进行克隆和变异后，对得到的新抗体按照适应度值进行选择。最终选择N个最优抗体进入下一代中。

3.2.3 抗体修正算子的设计

值得指出的是，在本文中每个个体是由各个数据点的类别组成的，这种编码方式使得个体的编码过长，而且产生的个体具有很大的随机性，更重要的是图谱划分准则的优化是一个NP难的问题。免疫克隆选择算法要想获得较好的解，需要很大的迭代次数。

在权核k均值算法的框架中，在给定初始划分的基础上，一般根据每个数据点xi与各个聚类中心的距离来产生数据的新划分，实际上这个处理恰恰是利用了数据之间的关系来产生新的划分。为了克服提出的算法收敛过慢的缺点，受权核k均值算法框架的这一处理的启发，定义一个个体修正算子，对随机产生的个体进行修正，使得个体以更快的速度向更优的方向进化。

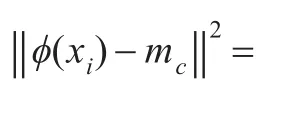
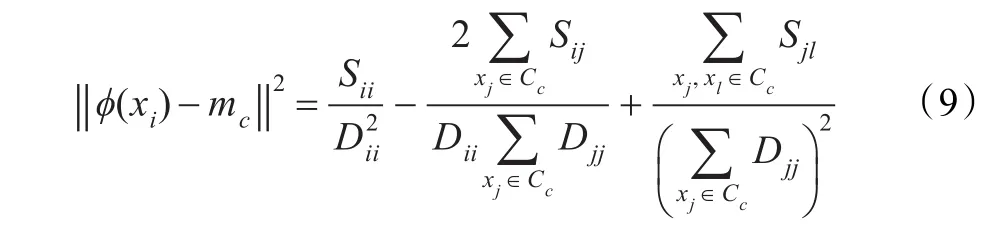
注意到式（9）中的第一项对于数据点xi来说是常数，式（9）可以被进一步简化为：

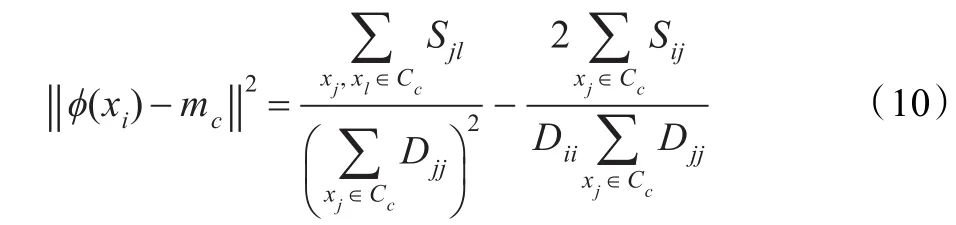
在对初始种群中的每个个体进行克隆操作之前，先利用式（10）按照数据点xi与各个聚类中心的距离产生一个修正后的新个体，然后计算修正后的个体的适用度函数值，如果修正后的个体的适用度函数值大于修正前的，那么就用修正后的个体替代修正前的个体，否则保持不变。对于变异后的个体，在进行选择操作之前，也可进行上述操作，如果修正后的个体的适用度函数值大于修正前的，那么就用修正后的个体替代修正前的个体，否则保持不变。通过实验发现，通过这一操作大大加快了算法的收敛速度。

4 验证实验及结果评价

在文献[6]中，已经验证了免疫克隆选择图划分方法比传统的谱聚类算法要具有更好的性能。在文献[13]中，作者也已用实验证明了密度敏感的半监督谱聚类（DS_SSC）[10]的性能要优于文献[14]的受限的完全连接层次聚类算法和文献[15]的受限的谱聚类算法。因此在实验中，仅将提出的新算法（ICS-SGP）与DS_SSC进行比较。本文所有实验中成对限制的数目取自0～200之间。对于每一个给定的限制数目进行20次实验，对平均结果进行比较。由于所选限制的不同对于聚类算法的性能有着很大的影响，为了实验的公平性，对于同一个限制数目产生的20组限制必须是不同的。在文献[6]中，指定免疫克隆选择图划分算法（ICS-GP）和密度敏感谱聚类（DS-SC）采用同样的参数设置，确保了各个算法竞争的公平性，对于USPS数据集和UMIST人脸数据集，ρ=erho，rho参数变化范围分别为[2-9,2-8.9,…,2-5]和[2-8,2-7.9,…,2-4]。同样的，ICS-SGP和DS-SSC算法也涉及到参数选择问题。对于所有实验，采用ICS-GP在每个数据集上取得最优性能（利用聚类正确率[16]来衡量算法的性能）下的参数作为ICS-SGP和DS-SSC算法的参数。为了公平起见，还给出了两种算法在DS-SC算法的最优参数（DS-SC算法取得最优性能下的参数）下的实验结果。

4.1 USPS数据集

本节选择了USPS数据集作为测试数据，将新算法应用于手写体数字识别中。USPS数据集是由9 298个灰度图像构成，其中包含7 291个训练样本，2 007个测试样本。实验取全部测试样本作为聚类数据集，从中挑选三组较难识别的{0，8}、{3，5，8}、{3，8，9}数字集合进行识别，表1给出了这三个手写体数据集的描述。对于这三个数据集，ICS-GP算法的最优参数rho1分别为2-6.1、2-5.7和2-5.6，DS-SC算法的最优参数rho2分别为2-6.0、2-5.7和2-5.8。图1中给出了ICS-SGP和DS-SSC对这三组手写体数字集合的识别性能随成对限制信息数目变化的曲线。

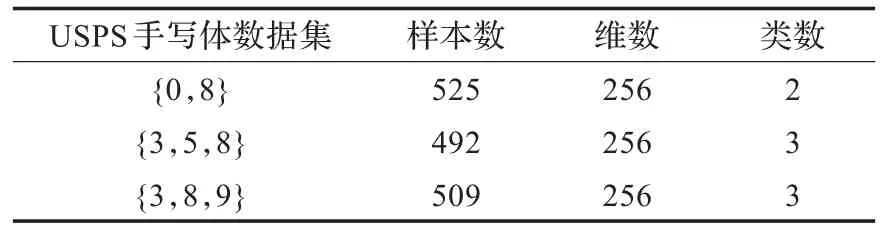
表1 USPS手写体数据集

从图1可以看出，当不提供成对限制信息时（即在图中的初始点处），对于所有数字集合，ICS-GP算法在参数rho1下的聚类性能要优于其在参数rho2下的结果，但是相差无几，表明对于USPS数据集，ICS-GP算法对于参数相对不敏感；DS-SC算法在参数rho2下的聚类性能要优于其在参数rho1下的结果，对于除了{0，8}以外的其他的数据集，DS-SC算法在两个参数下的结果相差很多，表明对于USPS数据集，DS-SC算法对于参数相对较敏感。在图中的初始点处，ICS-GP在任一参数下的聚类性能都要明显优于DS-SC算法在任一参数下的结果。

当逐步加入成对限制信息后，ICS-SGP在两个参数下的聚类性能都得到了逐步提高的同时，在两个参数下的聚类性能仍保持相差不多；DS-SSC算法随着成对限制信息的增多，对于除了{0，8}以外的其他的数据集，在参数rho2下的聚类性能还是明显优于其在参数rho1下的结果。可以看到，DS-SSC在任一参数下的聚类性能还是要低于ICS-SGP在任一参数下的聚类性能，表明对于手写体数据集，ICS-SGP的性能明显优于DS-SSC算法。需要注意的是，随着成对限制数目的增加，两个算法的聚类正确率并不总是随之增加，有时甚至出现了聚类准确率下降的现象。这主要是因为在此限制数目下，20次实验随机产生的限制信息不够理想，如果增加重复实验的次数，性能曲线会变化的平坦一点。

图1 USPS手写体数字集的实验对比结果

4.2 UMIST人脸数据集

UMIST人脸库是由20个人在相同的光照、不同的姿态（从侧面到正面）条件下，总共564张灰度图像组成，图像大小均为92×112。为了下面实验叙述方便，对Umist_cropped中的20个人按照{1，2，…，20}进行排序。在本文实验中，将人脸图像下采样为46×56像素大小，从中挑选两组连续的人脸数据集{1，2，3，4，5}和{6，7，8，9，10}，以及随机抽取的两组数据集{4，9，12，14，16}和{8，13，14，16，17}作为测试数据，表2给出了这人脸数据集的描述。对于这四个数据集，ICS-GP算法的最优参数rho1分别为2-5.7、2-4.1、2-5.0和2-4.2，DS-SC算法的最优参数rho2分别为2-4.3、2-4.6、2-5.2和2-4.8。在图2中给出了DS-SSC和ICS-SGP对这四组人脸数据集的识别性能随成对限制信息数目变化的曲线。

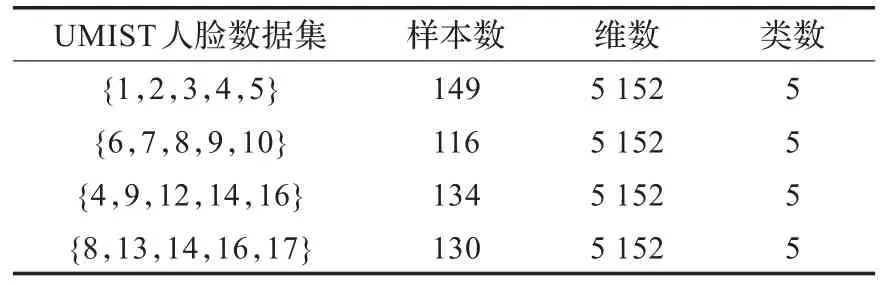
表2 UMIST人脸数据集

从图3可以看出，在图中的初始点处，ICS-GP在rho1参数下的聚类性能要优于其在rho2参数下的结果；DS-SC在rho2参数下的聚类性能要优于其在rho1参数下的结果。在rho1参数下，ICS-GP的聚类正确率要高于DS-SC；在rho2参数下，DS-SC的聚类正确率要高于ICS-GP。除了{1，2，3，4，5}数据集以外，ICS-GP在rho1参数下的聚类性能都优于DS-SC算法在任一参数下的结果。

随着成对限制信息的增加，ICS-SGP在rho1参数下的聚类性能仍保持优于其在rho2参数下的结果；除了{1，2，3，4，5}数据集之外，DS-SSC算法在参数rho2下的聚类性能基本上还是优于其在参数rho1下的结果。对于这四个数据集，在rho1参数下，对于每一个限制信息数目，ICS-SGP的聚类正确率几乎都要高于DS-SSC。然而除了{1，2，3，4，5}数据集以外，在每一个限制信息数目下，rho2参数下的ICS-SGP的聚类正确率几乎都要高于DS-SSC。另外，rho1参数下的ICS-SGP在每一个限制信息数目下的聚类结果基本上都是这两个算法在任一参数下最优的，而且除了{1，2，3，4，5}数据集以外，ICS-SGP在rho2参数（DS-SC的最优参数）下的结果也都基本上要优于DS-SSC在任一参数下的结果，这充分表明了ICS-SGP在人脸识别问题中具有优于DS-SSC的性能。和前面的手写体数据集实验一样，随着成对限制数目的增加，两个算法的聚类正确率也出现了聚类准确率下降的现象，同样如果增加重复实验的次数，性能曲线会变化的平坦一点。

5 结束语

本文提出了一种新的半监督聚类算法：半监督免疫克隆选择图划分算法。新方法利用成对限制信息和最短路径距离测度来构造样本点之间的相似性测度，并采用免疫克隆选择优化方法来优化图谱划分准则来获得最终的聚类结果，手写体数字和人脸数据集上的仿真实验表明了新算法具有的良好性能。值得指出的是，给定的成对限制信息理想与否对于聚类结果有很大的影响，这一点可以从实验结果中明显看出。因此，将信息量更丰富的限制信息，例如相对比较限制信息，引入到半监督免疫克隆选择图划分算法中是下一步的工作。

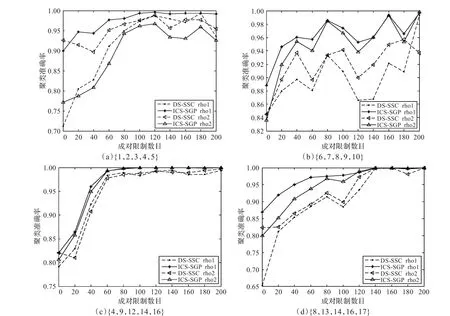
图2 UMIST人脸数据集的实验对比结果

[1]Fiedler M.Algebraic connectivity of graphs[J].Czechoslovak Mathematical Journal，1973，23（98）：298-305.

[2]Shi J，Malik J.Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22（8）：888-905.

[3]Ng A Y，Jordan M I，Weiss Y.On spectral clustering：Analysis and an algorithm[C]//Dietterich T G，Becker S，Ghahramani Z.Advances in Neural Information Processing Systems（NIPS）14.Cambridge：MIT Press，2002.

[4]高尚兵，周静波，严云洋.一种新的基于超像素的谱聚类图像分割算法[J].南京大学学报：自然科学版，2013，49（2）：169-175. [5]焦李成，杜海峰，刘芳，等.免疫优化计算学习与识别[M].北京：科学出版社，2006.

[6]刘汉强.免疫克隆选择图划分方法[J].计算机应用研究，2012，29（9）：3516-3520.

[7]Dhillon I S，Guan Y，Kulis B.Weighted graph cuts without eigenvectors：a multilevel approach[J].IEEE TransactionsonPatternAnalysisandMachineIntelligence，2007，29（11）：1944-1957.

[8]Hagen L，Kahng A B.New spectral methods for ratio cut partitioning and clustering[J].IEEE Transactions on Computer-Aided Design，1992，11（9）：1074-1085.

[9]Ding C，He X，Zha H，et al.A min-max cut algorithm for graphpartitioninganddataclustering[C]//Proceedings of ICDM，2001：107-114.

[10]Meila M，Xu M.Multiway cuts and spectral clustering[R]. U.Washington Tech Report，2003.

[11]杨光军.基于文化免疫克隆算法的关联规则挖掘研究[J].计算机工程与应用，2013，49（15）：113-115.

[12]马玉新，解建仓，罗军刚.基于免疫克隆选择算法的马斯京根模型参数估计[J].计算机工程与应用，2010，46（34）：208-212. [13]王玲，薄列峰，焦李成.密度敏感的半监督谱聚类[J].软件学报，2007，18（10）：2412-2422.

[14]Klein D，Kamvar S D，Manning C D.From instance-level constraints to space-level constraints：Making the most of prior knowledge in data clustering[C]//Sammut C，Hoffmann A G.Proc of the 19th Int’l Conf on Machine Learning. Sydney：Morgan Kaufmann Publishers，2002：307-314.

[15]Xu Q J，DesJardins M，Wagstaff K.Constrained spectral clustering under a local proximity structure assumption[C]// Russell I，Markov Z.Proc of the 18th Int’l Conf of theFloridaArtificialIntelligenceResearchSociety，Clearwater Beach.Florida：AAAI Press，2005.

[16]Wu M，Schölkopf B.A local learning approach for clustering[C]//Schölkopf B，Platt J，Hofmann T.Advances in Neural Information Processing Systems.USA：MIT Press，2007：1529-1536.

LIU Hanqiang

School of Computer Science,Shaanxi Normal University,Xi’an 710119,China

Using some prior information can significantly improve the performance of clustering algorithms.In order to solve the NP-hard graph partitioning problems and utilize some prior information,a semisupervised immune clone selection graph partition algorithm the pairwise constraint information is introduced into the similarity measure in the graph partitioning algorithms,then the immune clonal selection algorithm is utilized to optimal the criterion of the graph partitioning based on the corresponding similarity matrix to obtain the solution.The experimental results on the USPS handwritten digit datasets and UMIST face datasets show that the novel method is effective.

pairwise constraint information;immune clonal selection algorithm;graph partition

在聚类过程中利用一定量先验信息会显著提高聚类算法的性能。为了解决求解图谱划分方法NP难的问题并合理地利用一定量的先验信息，将成对限制信息引入到图谱划分方法中样本点的相似性测度，并在获得的相应的相似性矩阵的基础上，利用免疫克隆选择优化方法来优化图谱划分准则，提出了半监督免疫克隆选择图划分方法。USPS手写体数字集和UMIST人脸数据集识别的仿真实验证明了新方法的有效性。

成对限制信息；免疫克隆选择算法；图划分

A

TP391；TN911.73

10.3778/j.issn.1002-8331.1402-0449

国家自然科学基金（No.61202153，No.61102095）；陕西省自然科学基础研究计划资助项目（No.2012JQ8045，No.2014JQ8336）；陕西省科学技术研究发展计划资助项目（No.2014KJXX-72）。

刘汉强（1981—），男，博士，副教授，研究领域为模式识别，图像处理。E-mail：liuhq@snnu.edu.cn

2014-03-03

2014-06-03

1002-8331（2014）22-0011-06

CNKI网络优先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1402-0449.html