基于核估计的超定混合共轭盲信号分离方法

李炜，杨慧中

1.江南大学教育部轻工过程先进控制重点实验室，江苏无锡 214122

2.安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000

基于核估计的超定混合共轭盲信号分离方法

李炜1，2，杨慧中1

1.江南大学教育部轻工过程先进控制重点实验室，江苏无锡 214122

2.安徽工程大学安徽省电气传动与控制重点实验室，安徽芜湖 241000

1 引言

作为一种功能强大的信号处理方法，盲源分离（Blind Source Separation，BSS）近年来已成为无线通信、雷达、图像和生物医学信号分析等诸多领域的研究热点[1-3]。自从盲源分离问题被提出，至今已有二十余年。这期间诞生了诸多高效实用的算法用于求解不同类型的BSS问题[4-6]。其中，最具影响力的要属由法国学者Comon[7]首先提出的独立分量分析（Independent Component Analysis，ICA）方法，甚至在某些文献中对BSS和ICA并不加以区分。Comon给出了ICA在数学上明确的定义以及求解ICA问题的理论框架，从而将BSS问题转化为代价函数的构建和优化问题。以ICA为基础，Bell等人提出了一种基于随机梯度算法（Stochastic Gradient Algorithm）的最大化输出信息熵的BSS方法[8-9]。该算法可成功地实现超高斯信号的盲分离。但在实际应用中，由于随机梯度算法自身的限制，在运行过程中容易陷入局部极大值而导致算法的失败；并且，此算法中包含逆矩阵的计算，使得算法不稳定的同时还引入了很大的计算量；另外，该算法中还含有一个非线性激活函数仅仅凭经验选取的问题，对于不同类型的信号，非线性函数的选取也有所不同。

针对这些问题，Amari[10-12]提出了更加稳定和高效的自然梯度算法（Natural Gradient Algorithm）。与常规梯度算法相比，自然梯度算法具有更快的收敛速度，同时由于避免了矩阵逆的计算，使得算法的稳定性更强，但非线性函数只能凭经验选取的问题依旧存在。这也是目前许多BSS方法中普遍存在的问题，使得这些方法都只能分离单一统计特性的源信号[9，11]。当源信号中同时混有超高斯信号和亚高斯信号时此类分离算法将失效。

上述算法都是在假设源信号和混合信号数目相等的情况下提出的。而现实中往往源信号的个数是未知的，甚至可能是变化的，因此并不能始终保证盲分离模型中混合矩阵是可逆的方阵。本文针对超定混合矩阵的情形提出了一种快速、高效的BSS方法。该方法首先推导了基于最小化互信息准则的超定BSS代价函数，采用共轭梯度优化算法对改代价函数进行寻优得到分离矩阵的更新公式，并利用核密度估计方法对分离信号的概率密度函数及其导数进行在线估计，从而直接估计出各个信号分量的评价函数，而非经验性地去挑选非线性激活函数。仿真结果表明，与传统梯度方法和自然梯度方法相比，所提算法具有更快的收敛速度并且能同时分离出超高斯和亚高斯信号，因此具有更加广泛的应用范围。

2 超定盲分离问题描述

其中，A为m×n维的未知线性超定混合矩阵，且m＞n，即混合信号维数多于源信号维数，n(t)=[n1(t),n2(t),…,nm(t)]T为m维加性噪声信号，且噪声与信号之间相互独立，如图1所示。盲分离的目标是在未知混合矩阵的先验信息的情况下，求得一个n×m维分离矩阵B，使得通过对观测信号x(t)进行变换：

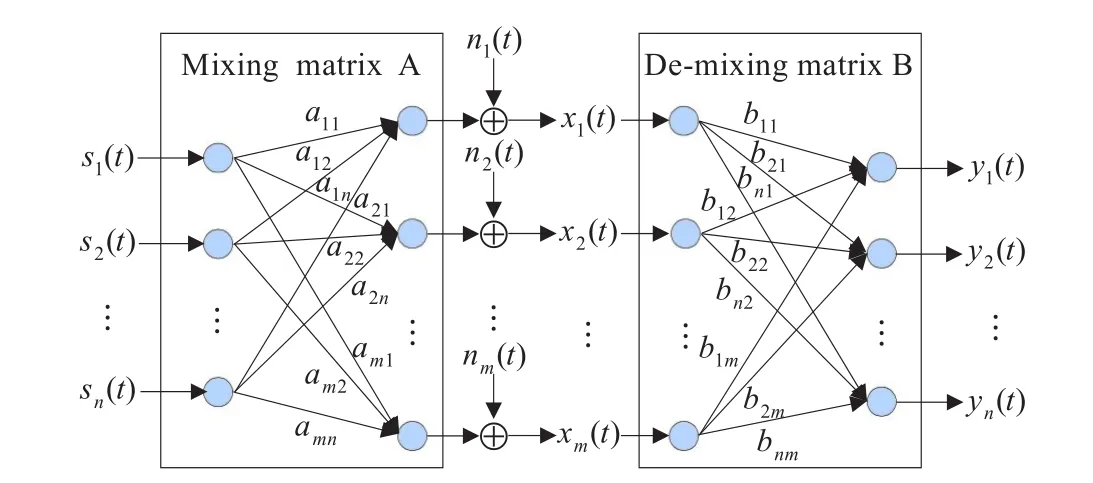
图1 线性超定盲源分离模型结构框图

而得到的信号y(t)=[y1(t),y2(t),…,yn(t)]T是源信号s(t)的估计，即y(t)和s(t)之间满足关系：y(t)=PDs(t)，其中P为任意排列矩阵，D为对角矩阵。

3 基于互信息的超定盲分离算法

本章首先给出基于互信息准则的超定盲分离代价函数，然后推导出相应的随机梯度算法和自然梯度算法。

3.1 超定盲分离的代价函数

由于假设源信号s(t)的各个分量之间是彼此统计独立的，所以可以通过合适的分离变换使得分离信号y(t)亦统计独立，从而恢复出源信号。信号之间的相互独立程度可以用互信息来度量，而互信息常用如下Kullback-Leibler散度来近似：

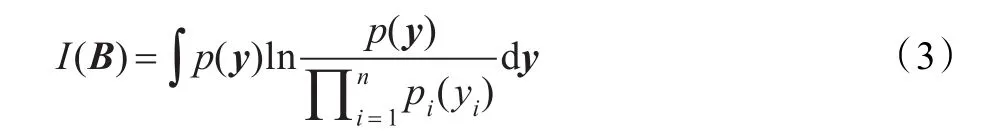
其中，p(y)为分离信号y的联合概率密度函数，pi(yi)为y各个分量的边缘概率密度函数。式（3）也可表达为如下微分熵的形式。

其中，H(y)=-E{lnp(y)}=-∫p(y)lnp(y)dy定义为y的联合微分熵，而H(yi)定义为各个分量的边缘微分熵。

由第2章描述可知，分离矩阵B是一个维数为n×m的矩阵，因而可对其进行奇异值分解：

其中，V为n×n维的正交矩阵，U为m×m维的正交矩阵，Σ为n×n维对角矩阵，其对角线元素为B的奇异值，0为n×(m-n)维零矩阵。将U分块为，并结合式（2）得到：

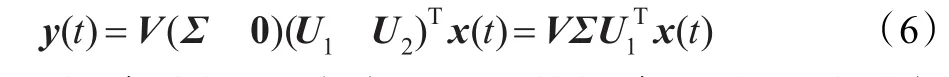
其中，矩阵乘积VΣ亦为一n×n维矩阵，因此y的联合概率密度函数p(y)可表示为：

其中，|·|表示标量的绝对值，det(·)表示矩阵的行列式。由微分熵定义，有

3.2 超定盲分离算法

为求得最优分离矩阵，需要求解下列无约束最优化问题：

下面推导最小化互信息代价函数式（11）的随机梯度算法和自然梯度算法。首先计算I(B)的梯度∇BI(B)。式（11）中等号右边第1项关于分离矩阵第i-j个元素bij的梯度为：

其中，μ(k)为算法的学习率。由于随机梯度算法内在的一些缺点：局部极值、收敛速度慢以及逆矩阵的计算等；又因为优化问题（12）的解为矩阵，因此其解空间为黎曼空间而非欧几里德空间，而在黎曼空间中最速下降方向为自然梯度方向，因此可以将上述随机梯度算法推广为自然梯度算法。代价函数I(B)式关于B的自然梯度为：

其中，I为单位矩阵。自然梯度算法（20）具有以下优点：当分离矩阵的初始值设定为行满秩时，最终得到的分离矩阵必为行满秩矩阵；无需进行矩阵逆的计算。

4 计算评价函数

由于信号的概率密度是未知的，因而现有的盲源分离算法普遍采用非线性函数代替信号的评价函数。而对于超高斯信号和亚高斯信号，需要选取不同的非线性函数。例如：对于超高斯信号，可以选取ϕsup(x)=αx+ tanh(βx),α≥0,β≥2；对于亚高斯信号，可以选取ϕsub(x)=当源信号中同时存在超高斯信号和亚高斯信号时，此类算法将无法实现信号的盲分离。针对该问题，通常的做法是在算法每步迭代过后都计算一次分离信号各个分量的峭度，依据该峭度值选取相应的非线性函数来充当该信号分量的评价函数。但此类算法会重复的估计信号高阶统计量，从而鲁棒性较差。

本文采用核密度估计法估计分离信号各个分量的概率密度函数，进而可以直接近似计算出对应的评价函数。该方法具体细节如下：假设有T组输出信号的观测样本y(1),y(2),…,y(T)。可以依据核概率密度估计法[13-14]，按照下式估计信号的概率密度函数：

5 基于共轭梯度的超定盲分离优化算法

共轭梯度算法的优越性能已经在神经学习领域得到了证明[16]。本章将共轭梯度的思想引入到分离矩阵的计算中。概括说，在每步迭代更新分离矩阵时，主要包含两部分的计算：首先在当前迭代点位置寻找到与当前搜索方向共轭的方向；然后沿着新的搜索方向计算新的迭代点。

首先，随机选择初始分离矩阵B(0)，并由式（19）计算在当前位置的自然梯度以确定下一步的搜索方向，然后依据式（20）直接计算出新的迭代解B(1)。从B(2)开始将使用共轭梯度算法来寻找其位置。

当求得迭代点B(k)(k≥1)以后，从点B(k-1)到点B(k)的搜索轨迹在B(k)位置的切向量可由下式计算：

其中，TB(k-1)表示算法在B(k-1)位置的搜索方向。再计算出当前位置的自然梯度I(B(k))，从而新的搜索方向TB(k)将由自然梯度和B(k)位置的切向量方向共同确定：

通过合理地选择参数a(k)可以实现新搜索方向与之前搜索方向之间共轭。通常可以选择：

其中，H(·)为海塞矩阵。实际计算中可以用有限差分近似方法来计算海塞矩阵，从而

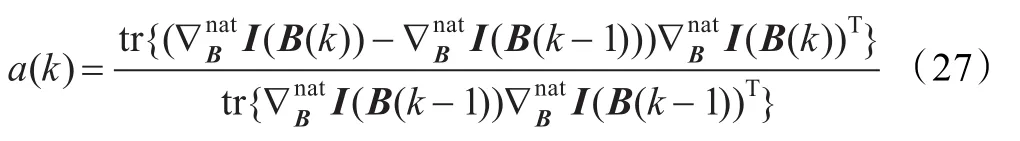
在计算得到新的搜索方向TB(k)之后，需要沿着新的搜索路径计算出下一个最优迭代点B(k+1)。可以通过二次插值方法求解如下一维优化问题来计算B(k+1)：

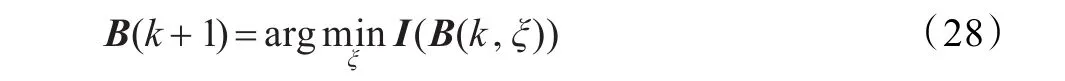
其中，I(B(k,ξ))即为互信息代价函数式（11），而B(k,ξ)表示新的搜索轨迹，具有如下数学描述：

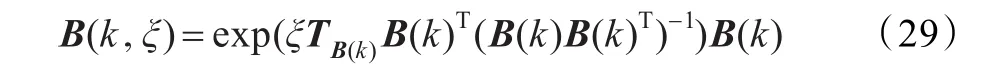
其中，参数ξ在区间[0,1]上取值，当ξ=0时，B(k,ξ)即为起始点B(k)。

具体的算法步骤如下：

（1）初始化：令迭代序数k=0，最大迭代次数为观测信号的样本数T，随机生成初始分离矩阵B(0)，选择度量算法性能的评价指标，如式（30）中的PI，并给其设定一个合适的阈值。

（2）依据式（2）计算对应的分离信号y(0)，利用第4章中给出的核概率密度方法估计其各个分量的概率密度函数pi,τ(yi(0)),i=1,2,…,n，进而计算出评价函数向量φ(y(0))。以自然梯度方向为搜索方向，即直接由算法（20）计算第一个迭代解B(1)，进而计算分离信号y(1)。

（3）令k=k+1，依据式（24）计算从点B(k-1)到点B(k)的搜索轨迹在B(k)位置的切向量T′B(k)。

（4）计算评价函数φ(y(k))，并计算自然梯度

（5）由式（27）计算参数a(k)。

（6）由式（25）计算出新的搜索方向TB(k)。

（7）沿着新的搜索路径B(k,ξ)求解优化问题（28）以求得新的迭代解B(k+1)，并计算新的分离信号y(k+1)。

（8）计算当前的盲分离算法性能评价指标的数值。

（9）判断算法是否满足结束条件。当满足如下两种情况中的任意一种时，则继续步骤（10），否则跳转至步骤（3）再次循环执行上述过程：①迭代序数已达到最大迭代次数，即k=T；②算法的性能已达到设定的评价指标的阈值。

（10）终止算法并输出分离信号y(k+1)作为源信号的估计。

6 仿真实验

本章采用若干计算机仿真算例来验证所提线性超定盲源分离算法的有效性，所涉及的算法程序均由Matlab语言编写。首先通过分离同时包含有超高斯和亚高斯信号的混合信号来观察算法实施的效果；然后通过与随机梯度算法和自然梯度算法相比较体现所提算法的优越性能。

采用如图2所示的5个信号作为源信号，其中s1和s2为声音信号，因此都是超高斯的；而s3，s4和s5则为合成的亚高斯信号。为了验证算法在超定情况下的效果，在这里混合矩阵采用一个7×5维的随机矩阵，其内各元素取值服从区间[0,1]的均匀分布。依据式（1）可得到混合信号如图3所示。

图23 个亚高斯信号和2个超高斯信号构成的源信号

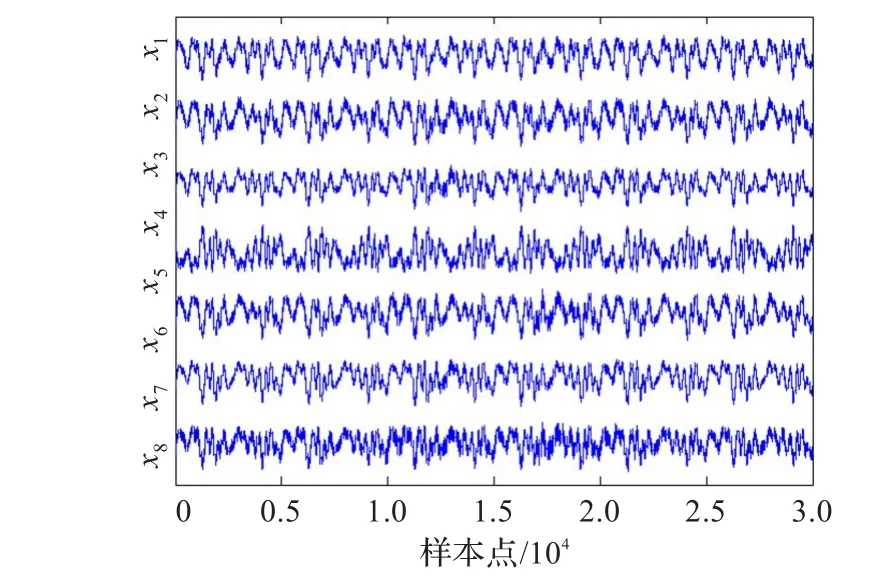
图3 超定混合模型下生成的混合信号

对图3中所示的混合信号应用本文所提出的基于共轭梯度和评价函数估计的超定盲分离算法。其中初始分离矩阵选择为随机生成的5×7维矩阵。分离得到的信号波形如图4所示。对比图4和图2，能够直观地看出所提算法可以在线性超定混合模型，并且同时包含有超高斯信号和亚高斯信号的情况下成功地恢复出各个源信号的波形。

为了体现出基于共轭梯度的盲源分离算法的优越性，下面分别执行共轭梯度算法和在第3.2小节中导出的随机梯度盲分离算法（18）和自然梯度盲分离算法（20），并对于每种算法的分离结果计算其盲分离性能指标PI值。PI定义如下：

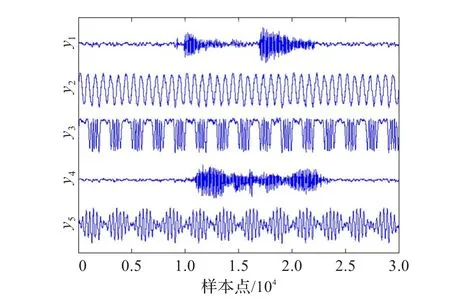
图4 文中所提超定盲分离算法计算得到的分离信号

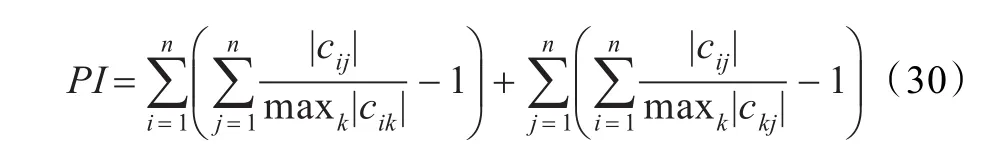
其中，cij为全局矩阵C=BA中的第i行第j列元素，n为源信号的个数。当矩阵C的每行和每列都只有一个元素占优而其余元素近似为零时，PI取值就小。而PI的值越小，则表明盲分离算法的分离效果越好。

为了简便起见，做如下标记：共轭梯度算法：CGA；随机梯度算法：SGA；自然梯度算法：NGA。独立重复的运行上述三种算法各100次，并计算出各算法的平均性能指标。三种盲分离算法的平均PI学习曲线如图5所示。从图中可以观察到，较之另外两种算法，CGA算法的收敛速度和分离精确度都得到了提高。而在欧几里德空间中运行的随机梯度算法的性能是三者中最差的。

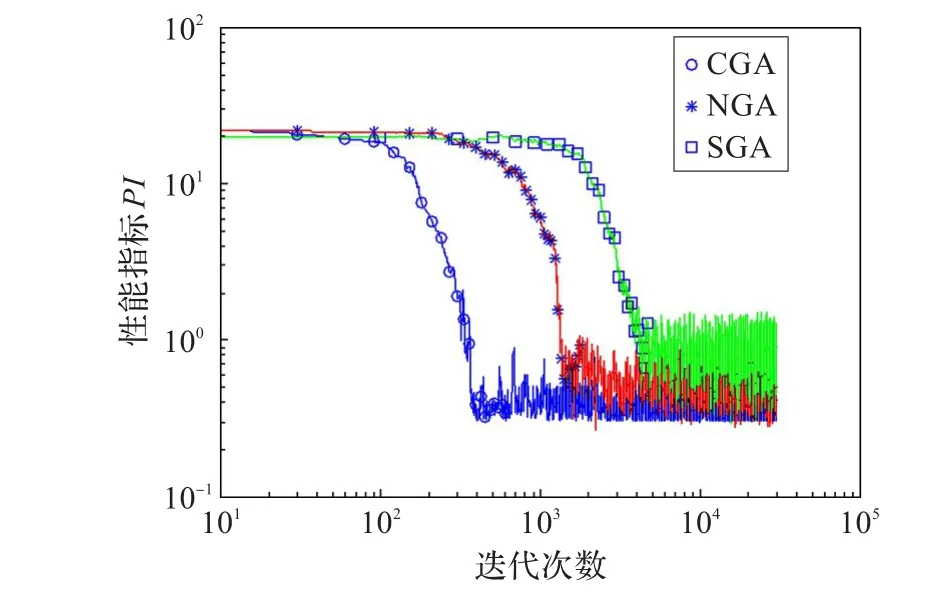
图5 三种盲源分离算法的比较：平均PI的学习曲线

需要指出的是，SGA算法中包含有矩阵逆的计算过程，当矩阵接近奇异时算法会因不能收敛到最优点而失效。因此，图5中SGA算法的平均PI值是剔除掉那些失败的试验后计算得到的结果。为了说明这个问题，再次执行上述三种盲分离算法。每种算法独立执行15次，并计算出每次的PI，将其绘于图6中。

从图6可以看出，SGA算法在第2次和第6次试验时发生了发散的情况，使得PI出现了很大数值，而另外两种算法则没有发生此种情况。此外，再次观察到CGA算法的分离精确度总体上要优于其他两种算法。

除了利用式（30）作为指标来度量算法的性能以外，下面从其他几个方面来全面分析以上各种算法的表现。首先，定义分离信号的归一化信号干扰比SIR：

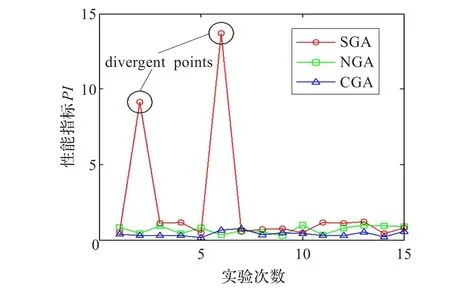
图615 次独立重复实验中三种算法不同的表现（黑色圆圈圈出的点表示SGA算法运行失败）

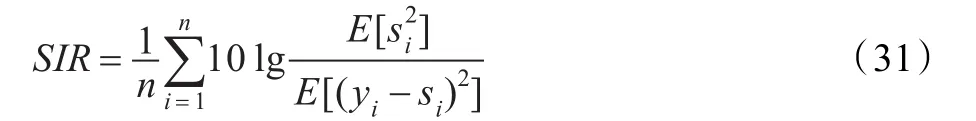
其中，n为源信号的个数，yi为重新排列后与第i个源信号si对应的分离信号。然后给PI设定一个阈值0.5，当算法达到该阈值时，分别计算和记录下各个算法的信号干扰比，所迭代的步数以及运行Matlab程序所消耗的时间。再次独立重复地运行上述三种算法各100次，计算得到各项指标的平均值，如表1所示。

表1 三种算法各项性能的比较

从表1可以看出算法CGA除了在收敛时间上略高与NGA以外，其他各项指标都要优于另外两种算法。

7 结束语

本文研究了线性超定混合情况下的盲源分离问题。在混合信号多于源信号的条件下，首先以互信息原理作为分离信号独立性的度量，通过对分离矩阵进行奇异值分解操作化简得到了超定盲源分离问题的代价函数。然后用共轭梯度优化算法对该代价函数进行优化推导出了分离矩阵的学习公式。在训练过程中，每当新的迭代点被计算出以后，都要计算该点在黎曼空间中的自然梯度值用来确定算法的搜索方向。另外，算法中的评价函数项则直接利用核密度估计方法估计得到。数值仿真验证了所提超定盲分离算法的可行性，并且在源信号中同时含有超高斯信号和亚高斯信号时依旧有效。通过与随机梯度算法和自然梯度算法的对比可以看出，本文所提算法具有更好的分离性能。

[1]肖正安.改进FOA算法在语音信号盲分离中的应用[J].计算机工程与应用，2013，49（16）：201-204.

[2]赵文红，王巍.盲源分离技术在AIS中的应用[J].计算机科学，2013，40（6）：217-219.

[3]曹军宏，韦灼彬，刘树勇.改进型盲源分离在结构模态识别中的应用[J].振动、测试与诊断，2013，33（4）：689-693.

[4]蒋照菁，辜方林，张杭.一种基于NPCA的自适应变步长盲源分离算法[J].计算机工程与应用，2013，49（8）：206-208.

[5]王放，何选森.蚁群聚类的欠定盲源分离方法[J].计算机工程与应用，2013，49（13）：211-215.

[6]郭靖，曾孝平.基于Hough变换的时频盲源分离算法[J].计算机工程与应用，2012，48（21）：26-30.

[7]Comon P，Jutten C.Handbook of blind source separation：independent component analysis and applications[M].United States：Academic Press，2010.

[8]Bell A J，Sejnowski T J.An information maximization approach to blind separation and blind deconvolution[J]. Neural Computation，1995，7：1129-1159.

[9]Liu D，Liu X.Informax algorithm based on linear ICA neural network for BSS problems[C]//Proceedings of the 4th World Congress on Intelligent Control and Automation，2002：1949-1952.

[10]Amari S.Natural gradient works efficiently in learning[J]. Neural Computation，1998，10：251-276.

[11]Choi S，Cichocki A，Zhang L L，et al.Approximate maximum likelihood source separation using the natural gradient[J].IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences，2003，E86-A（1）：198-205.

[12]Choi S，Amari S，Cichocki A.Natural gradient learning for spatio-temporal decorrelation：recurrent network[J].IEICE Transactions on Fundamentals of Electronics CommunicationsandComputerSciences，2000，E83-A（12）：2175-2722.

[13]Mittal A，Paragios N.Motion-based background subtraction using adaptive kernel density estimation[C]//Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition，2004：302-309.

[14]Jones M C，Sheather S J.A brief survey of bandwith selection for density estimation[J].Journal of the American Statistical Association，1996，91（433）：401-407.

[15]Karvanen J，Koivunen V.Blind separation methods based on Pearson system and its extensions[J].Signal Processing，2002，82（4）：663-673.

[16]Nishimori Y，Akaho S，Plumbley M D.Natural conjugate gradient on complex flag manifolds for complex independent subspace[C]//Proceedings of the 18th International Conference on Artificial Neural Networks，Lecture Notes in Computer Science，2008：165-174.

LI Wei1，2,YANG Huizhong1

1.Key Laboratory of Advanced Process Control for Light Industry of Ministry of Education,Jiangnan University,Wuxi, Jiangsu 214122,China
2.Anhui Key Laboratory of Electric Drive and Control,Anhui Polytechnic University,Wuhu,Jiangsu 241000,China

If there are more mixtures than source signals,the mixing matrix in the Blind Source Separation（BSS）problem is described as an over-determined matrix.As a result,the separation task can be realized through estimate the inverse of the mixing matrix directly.This paper presents a conjugate gradient based BSS method for such over-determined mixing case.The over-determined BSS cost function is first obtained based on the minimum mutual information principle combined with the singular value decomposition of the de-mixing matrix with full row rank.The conjugate gradient optimization algorithm is then exploited to deduce the training equations for the de-mixing matrix.In each of iterations,the score functions of the separation signals are estimated by a kernel probability density estimation method,avoiding the problem of many traditional BSS algorithm where the score functions should be replaced by specific nonlinear functions.The efficiency of the proposed over-determined BSS algorithm is validated by several simulations.

conjugate gradient;score functions;mutual information;over-determined mixtures

当混合信号的个数多于源信号时，盲源分离模型中的混合矩阵被描述为一个超定矩阵，因此不能直接通过估计逆矩阵的方法来得到分离矩阵。针对该线性超定混合情况提出了一种基于共轭梯度的盲源分离方法。该方法基于最小互信息准则，通过对行满秩分离矩阵的奇异值分解而引入了超定盲源分离的代价函数。利用共轭梯度优化算法推导出了迭代计算分离矩阵的更新公式。在每次迭代计算中，利用随机变量概率密度估计的核函数法在线估计分离信号的评价函数。避免了诸多传统盲分离算法中只能凭经验选取特定的非线性函数来代替评价函数的问题。仿真结果验证了所提算法的有效性。

共轭梯度；评价函数；互信息；超定混合信号

A

TN911.7

10.3778/j.issn.1002-8331.1403-0357

LI，Wei,YANG Huizhong.Blind separation of over-determined mixtures with conjugate gradient and kernel estimation.Computer Engineering and Applications,2014,50（22）：22-27.

国家自然科学基金（No.61273070）；高等学校学科创新引智计划资助（No.B12018）；江南大学博士研究生科学研究基金（No.1252050205135130）；江苏省普通高校研究生科研创新计划项目（No.CXZZ13_0739）。

李炜（1985—），男，博士研究生，研究领域为盲信号处理，独立分量分析；杨慧中（1955—），女，教授，博士生导师，研究领域为软测量，复杂工业过程的检测、建模与优化控制。E-mail：liweilwlcw@sina.com

2014-03-24

2014-06-06

1002-8331（2014）22-0022-06

CNKI网络优先出版：2014-06-26,http://www.cnki.net/kcms/doi/10.3778/j.issn.1002-8331.1403-0357.html