FI代数的模糊素MP滤子与模糊超MP滤子

刘春辉

1.赤峰学院 教务处，内蒙古 赤峰 024001

2.赤峰学院 数学与统计学院，内蒙古 赤峰 024001

FI代数的模糊素MP滤子与模糊超MP滤子

刘春辉

1.赤峰学院 教务处，内蒙古 赤峰 024001

2.赤峰学院 数学与统计学院，内蒙古 赤峰 024001

1 引言

Fuzzy蕴涵代数（简称：FI代数）是由我国学者吴望名于1990年提出的，作为对非经典逻辑代数中“蕴涵”连接词的代数化，它揭示了各种逻辑蕴涵算子的共同本质[1]。众多的逻辑代数系统，如MV代数（格蕴涵代数）、BL代数、R0代数（NM代数）、有界BCK代数以及剩余格等都可以看成是FI代数的特例，因此对FI代数结构的研究具有广泛而基本的重要意义。迄今为止，有关这方面的研究工作已经获得了很多有价值的研究成果[2-7]。

自从20世纪60年代美国著名的控制论专家Zadeh首次提出模糊集[8]的概念以来，模糊集的思想和方法已经被有效地应用于各个学科领域。近年来，国内外学者将这一思想和运算方法引入到逻辑代数的理想和滤子概念的研究，提出了多种形式的模糊理想和模糊滤子概念，并针对它们的特性和相互关系做了许多重要的研究工作，提出了大量有意义的研究课题并获得了一批优秀的研究成果[9-14]。为了进一步揭示FI代数的结构特征，文献[15]在FI代数中引入了多种模糊MP滤子概念，并对它们的性质和相互关系进行了细致的探讨，以此为基础，本文继续对FI代数的模糊MP滤子概念作深入研究，引入模糊素MP滤子和模糊超MP滤子概念并考察其特性，获得了一些有意义的结果。

2 预备知识

定义1[1]（Fuzzy蕴涵代数）（2，0）型代数(X，→，0)称为Fuzzy蕴涵代数，简称FI代数，若 x，y，z∈X

FI-1：x→(y→z)=y→(x→z)；

FI-2：(x→y)→((y→z)→(x→z))=1；

为了叙述简洁，以下如无特别说明，X均表示FI代数。文献[1]在 X上定义了一个偏序关系≤使得x≤y⇔x→y=1，∀x，y∈X 。同时，定义一元运算 c:X→X 使得c(x)=x→0。

引理1[1]任意 x，y，z∈X，下列结论成立：

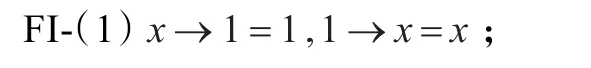
FI-（2）如果x≤y，则z→x≤z→y且y→z≤x→z。

定义2[7]设 X为FI代数，若(X，≤)构成并半格，即∀x，y∈X，x∨y都存在，则称 X为并半格FI代数。如果并半格FI代数X满足：

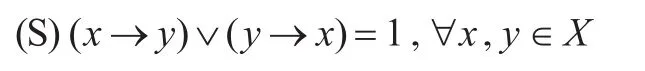
则称X为满足条件(S)的并半格FI代数。

引理2[4]设 X为并半格FI代数，则对任意的 x，y∈X，(x∨y)→y=x→y。

定义3[7]设∅≠F⊆X，如果（1）1∈F 且（2）∀x，y∈X，x，x→y∈F⇒y∈F，则称 F是 X的 MP滤子。X 的全体MP滤子之集记为FMP(X)。

定义4[7]设X为一个并半格FI代数，X≠P∈FMP(X)，如果 ∀x，y∈X，x∨y∈P蕴涵 x∈P或 y∈P，则称 F 是X的素MP滤子。

引理3[7]设 X为满足条件(S)的并半格FI代数，则X≠P∈FMP(X)是 X的素 MP滤子当且仅当∀x，y∈X，x→y∈P或 y→x∈P。

引理4[7（]素MP滤子定理）设X为并半格FI代数，S⊆X对∨关闭，F∈FMP(X)且 F∩S=∅。则存在 X的素MP滤子P使得F⊆P且P∩S=∅。

引理5[7]设 X为并半格FI代数，如果 F∈FMP(X)且x∉F。则存在X的素MP滤子P使得F⊆P且x∉P。

定义5[9]非空集合X上的一个模糊集指的是映射μ:X→[0，1]。设 μ是 X上模糊集，称集合 μt={x∈X| μ(x)≥ t}，∀t∈[0，1]为 μ的 t截集。

设μ和v为非空集合 X上的两个模糊集，定义 μ和v之间的模糊包含关系⊂如下：

μ⊂v当且仅当 μ(x)≤v(x)，∀x∈X

定义6[15]设 X为FI代数，称 X上的模糊集μ为X的模糊MP滤子，如果

注1设 X为FI代数，μ为 X的模糊MP滤子，则x≤y蕴涵 μ(x)≤μ(y)，即 μ是保序的。

引理6[8]X上的模糊集μ为X的模糊MP滤子当且仅当 ∀t∈[0，1]，μt=∅ 或 μt∈FMP(X)。

引理7[8]设 X为FI代数，则 X上的模糊集 μ为 X的模糊 MP滤子当且仅当 x→(y→z)=1蕴涵 μ(z)≥min{μ(x)，μ(y)}，∀x，y，z∈ X 。

3 FI代数的模糊素MP滤子

定义7设 X为FI代数，μ为X的非常值的模糊MP 滤子。如果 ∀t∈[0，1]，μt=∅ 或当 μt≠X 时，μt为X的素MP滤子，则称μ为X的模糊素MP滤子。

定理1设X为并半格FI代数，则X的非常值模糊MP滤子μ为X的模糊素MP滤子当且仅当对任意的x，y∈X，μ满足：

证明设μ是 X的非常值的模糊MP滤子且满足条件（FPF1）。对任意的 t∈[0，1]，若 μt≠∅，则由引理6可知 μt∈FMP(X)。若 μt≠X 且 x∨ y∈ μt，则 μ(x∨y)≥t，于是由（FPF1）知：

从而 μ(x)≥t或 μ(y)≥t，进而 x∈μt或 y∈μt，故由定义4知 μt为 X的素 MP滤子。因此 μ为 X的模糊素 MP滤子。

反之，设 μ为 X的模糊素 MP滤子。令t=μ(x∨y)，则 x∨y∈μt，故由引理6知 μt∈FMP(X)。若 μt=X，则x，y∈μt，从而 μ(x)≥t=μ(x∨y)且 μ(y)≥t=μ(x∨y)，因此max{μ(x)，μ(y)}≥μ(x∨y)。若 μt≠X，则由题设条件知 μt为 X的素 MP滤子。因此 x∨y∈μt蕴涵 x∈μt或 y∈μt，从而 μ(x)≥t=μ(x∨y)且 μ(y)≥t=μ(x∨y)，进而亦有max{μ(x)，μ(y)}≥μ(x∨y)。因此（FPF1）。

注2设X为并半格FI代数，μ为X的非常值的模糊MP滤子。则由模糊MP滤子的保序性可知定理1中的条件（FPF1）等价于：

例1 设 X={0，a，b，1}且 0＜a＜b＜1，定义 X 上二元运算“→1”如表1所示。则利用如图1所示的MATHEMATICA程序可验证(X，→1，0)是一个FI代数。

表1 运算“→1”的定义

在 X 上定义模糊集 μ使得 μ(0)=μ(a)=0.2，μ(b)= 0.4，μ(1)=0.6，则容易验证 μ是 X的一个模糊素 MP滤子。

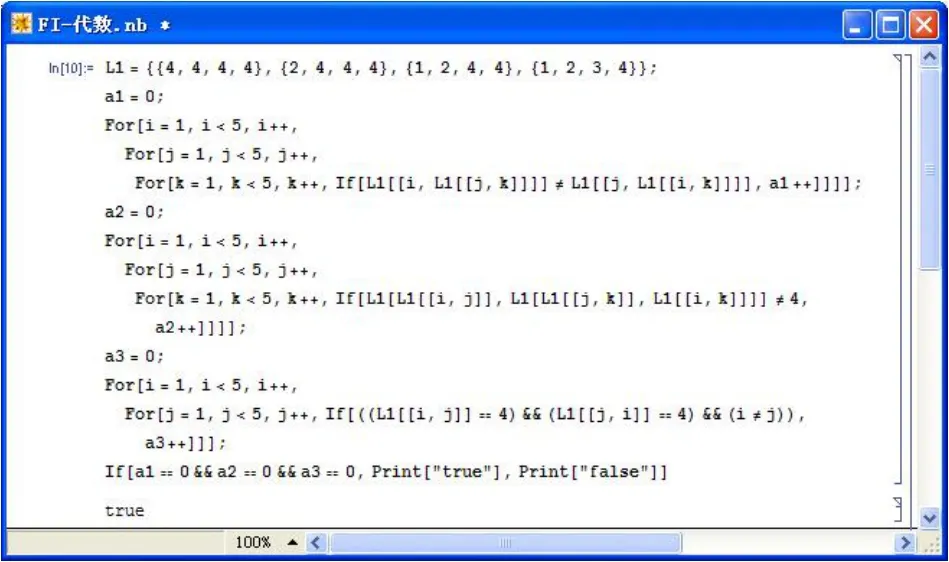
图1 验证FI代数的MATHEMATICA程序

定理2设X为并半格FI代数，则X的非常值模糊MP滤子μ为 X的模糊素MP滤子当且仅当μ(x∨y)= μ(1)蕴涵 μ(x)=μ(1)或 μ(y)=μ(1)，∀x，y∈ X 。

证明设是 X的模糊素 MP滤子，x，y∈X使得μ(x∨y)=μ(1)，则由（FPF2）可知 max{μ(x)，μ(y)}=μ(x∨y)= μ(1)，因此 μ(x)=μ(1)或 μ(y)=μ(1)。

反 之 ，设 μ(x∨y)=μ(1)蕴 涵 μ(x)=μ(1)或 μ(y)= μ(1)。假设 μ(x∨y)＞max{μ(x)，μ(y)}，则 μ(x∨y)＞μ(x)且μ(x∨y)＞μ(y)，因此 当 μ(x∨y)=μ(1)时有 μ(x)＜μ(1)且μ(y)＜μ(1)，这与题设条件矛盾。因此（FPF1）成立，从而μ为X的模糊素MP滤子。

定理3设X为满足条件(S)的并半格FI代数，则X的非常值模糊MP滤子μ为X的模糊素MP滤子当且仅当 Xμ为 X 的素 MP滤子。其中 Xμ={x∈X|μ(x)=μ(1)}。

证明 由 Xμ的定义，显然 Xμ=μμ(1)。因为 μ是 X的非常值模糊 MP 滤子，所以 μ(0)＜μ(1)，从而 0∉Xμ。又由1∈Xμ知 Xμ≠∅，故由定义7得 Xμ为 X的素 MP滤子。

反之，设 Xμ为 X的素MP滤子。则由引理2和引理 3知 ∀x，y∈X，(x∨y)→y=x→y∈Xμ或 (x∨y)→x= y→x∈Xμ。故 μ((x∨y)→y)=μ(1)或 μ((x∨y)→x)=μ(1)。因此由定义 6 可得 μ(x)≥min{μ((x∨y)→x)，μ(x∨y)}= μ(x∨y) 或 μ(y)≥min{μ((x∨y)→x)，μ(x∨y)}=μ(x∨y) 。故 μ(x∨y)≤max{μ(x)，μ(y)}成立，因此 μ 为 X 的模糊素MP滤子。

推论1设X为满足条件(S)的并半格FI代数，则X的非常值模糊MP滤子μ为X的模糊素MP滤子当且仅当对任意 x，y∈X，μ(x→y)=μ(1)或 μ(y→x)=μ(1)。

证明由定理3知μ为X的模糊素MP滤子当且仅当 Xμ为 X的素 MP滤子，而由引理3知这当且仅当x→y∈Xμ或 y→x∈Xμ，再由 Xμ的定义知这当且仅当μ(x→y)=μ(1)或 μ(y→x)=μ(1)。

证明设 F∈FMP(X)为 X的素 MP滤子，则 F≠X，从而 μF不为常值。设 x，y∈X，由条件(S)知(x→y)∨(y→x)=1∈F，所以由引理3知 x→y∈F或 y→x∈F，即 μF(x→y)=α=μF(1)或 μF(y→x)=α=μF(1)。因此由推论1知 μF为 X的模糊素MP滤子。

反之，设μF为 X的模糊素MP滤子，则由定理3知F=XμF为 X的素MP滤子。

推论2设 X为满足条件(S)的并半格FI代数，则F∈FMP(X)为 X的素MP滤子当且仅当 χF为 X的模糊素MP滤子。其中 χF为F的特征函数。

定理5（模糊素MP滤子的扩张定理）设X为满足条件(S)的并半格FI代数，μ和v为 X的两个模糊MP滤子，且满足μ⊂v和 μ(1)=v(1)。如果 μ为 X的模糊素MP滤子，则v也是X的模糊素MP滤子。

证明因为μ为X的模糊素MP滤子，所以由推论1得 μ(x→y)=μ(1)或 μ(y→ x)=μ(1)。若 μ(x→y)=μ(1)，则由 μ⊂v和 μ(1)=v(1)可得 v(1)=μ(1)=μ(x→y)≤v(x→y)，从而可得 v(x→y)=v(1)。类似可证若 μ(y→x)=μ(1)，则v(y→x)=v(1)。因此由推论1便得v也是 X的模糊素MP滤子。

定理6设X为满足条件(S)的并半格FI代数，μ为X的模糊素 MP滤子，k∈[0，μ(1))，则模糊集 μ∨k也是 X的模糊素 MP滤子。其中∀x∈X，(μ∨k)(x)=max{μ(x)，k}。

证明首先证明μ∨k是 X的模糊MP滤子。任取x，y，z∈ X，设x→(y→ z)=1，则由引理7得μ(z)≥ min{μ(x)，μ(y)}，从而

故再由引理7知μ∨k是X的模糊MP滤子。

其次证明μ∨k是X的模糊素MP滤子。因μ为X的模糊素 MP 滤子且 k＜μ(1)，故 (μ∨k)(1)=max{μ(1)，k}= μ(1)≠(μ∨k)(0)，否则 μ(1)=μ(0)，与 μ 非常值矛盾。又因为 ∀x∈X，(μ∨k)(x)=max{μ(x)，k}≥μ(x)，所以 μ⊂(μ∨k)，再注意到 (μ∨k)(1)=μ(1)，由定理5便得 μ∨k是 X 的模糊素MP滤子。

定理7设X为满足条件(S)的并半格FI代数，μ为X的非常值模糊MP滤子且μ(1)≠1。则存在X的模糊素MP滤子v使得 μ⊂v。

证明因为 μ为 X的非常值模糊 MP滤子，所以Xμ∈FMP(X)且 Xμ≠X。从而由引理5知存在 X的一个素MP滤子P使得Xμ⊂P。且由推论2又知 χP为X的模糊素 MP 滤子。令 v=χP∨k，其中 k=max{μ(x)|x∈XP}，则 k≤μ(1)＜1，因此由定理6知v为 X的模糊素 MP滤子且μ⊂v，∀x∈X。从而定理得证。

定理8（模糊素MP滤子定理）设 X为满足条件(S)的并半格FI代数，μ为 X的模糊 MP滤子，v为 X上的满足条件 v(x∨y)=min{v(x)，v(y)}的模糊集，∀k∈[0，μ(1))有 min{μ(x)，v(x)}≤k 。则存在 X 的模糊素 MP滤子 σ 使得 μ⊂σ 且 ∀k∈[0，μ(1))，min{σ(x)，v(x)}≤k。

证明 ∀k∈[0，μ(1))，令 S={x∈X|v(x)＞k}和 F={x∈X|μ(x)＞k} 。若 a，b∈S，则 v(a)＞k 且 v(b)＞k，从 而v(a∨b)=min{v(a)，v(b)}＞k，所以 a∨b∈S，这表明 S 对∨ 关闭。下证 F∈FMP(X)。事实上，由 ∀k∈[0，μ(1))知μ(1)＞k，从而1∈F。设x，x→y∈F，则μ(x)＞k且μ(x→y)＞k，故 min{μ(x)，μ(x→y)}＞k，从而由 μ 为 X 的模糊 MP滤子知 μ(y)＞k，进而 y∈F，故 F∈FMP(X)。又因为由∀k∈[0，μ(1))有 min{μ(x)，v(x)}≤k 可知 S∩F=∅，所以由素MP滤子定理知存在X的素MP滤子P使F⊂P且 P∩S=∅。令σ=χP∨k，则由定理6和推论2知σ为X的模糊素 MP滤子。若 x∈P，则σ(x)=max{1，k}= 1≥μ(x)。若 x∉P，则 x∉F，从而 μ(x)≤k=max{0，k}= σ(x)。因此总有 μ⊂σ。另一方面，若 x∈S，则x∉F，从而 x∉ P，故 σ(x)=max{0，k}=k，于是 min{σ(x)，v(x)}= k。若 x∉S，则 v(x)≤k，从而 min{σ(x)，v(x)}≤v(x)≤k。因此总有 ∀k∈[0，μ(1))，min{σ(x)，v(x)}≤k 。

4 FI代数的模糊超MP滤子

定义8设 X为FI代数，μ为 X的非常值的模糊MP滤子。称μ为 X的模糊超MP滤子，如果对任意的x∈X，μ满足：

（FUF1）μ(x)=μ(1)或 μ(c(x))=μ(1)。

例2 设 X={0，a，b，c，d，1}，定义 X 上二元运算“→2”如表2所示。则利用如图2所示的MATHEMATICA程序可验证(X，→2，0)是一个FI代数。

表2 运算“→2”的定义

在 X上定义模糊集 μ使得 μ(1)=μ(a)=μ(d)=0.7，μ(0)=μ(b)=μ(c)=0.3，则容易验证 μ是 X的一个模糊超MP滤子。

定理9设X为FI代数。则X的非常值的模糊MP滤子μ为X的模糊超MP滤子当且仅当μ满足：

图2 验证FI代数的MATHEMATICA程序

（FUF2）μ(x)≠μ(1)且 μ(y)≠μ(1)蕴涵 μ(x→y)=μ(1)且 μ(y→x)=μ(1)，∀x，y∈X 。

证明（FUF1）⇒（FUF2）：设 μ(x)≠ μ(1)且 μ(y)≠ μ(1)，因为 0≤y，所以 由 FI-（2）得 x→0≤x→y，即 c(x)≤x→y。于是由模糊 MP滤子 μ的保序性和（FUF1）得μ(x→y)≥μ(c(x))=μ(1)，因此 μ(x→y)=μ(1)。类似地，由μ(c(y))=μ(1)得 μ(y→x)=μ(1)。故（FUF2）成立。

（FUF2）⇒（FUF1）：设 μ(x)≠μ(1)，因为 μ为 X 的非常值模糊 MP 滤子，所以 μ(0)≠μ(1)，故由（FUF2）得μ(x→0)=μ(1)，即 μ(c(x))=μ(1)。因此由定义8知 μ 为 X的模糊超MP滤子。

定理10设X为满足条件(S)的并半格FI代数。则X的非常值的模糊集μ为X的模糊超MP滤子当且仅当μ是X的模糊素MP滤子且满足：

（FUF3）μ(x∨c(x))=μ(1)，∀x∈X 。

证明“充分性”：设 μ是 X的模糊素MP滤子且满足（FUF3）。设 x∈X，由注2可得 μ(x∨c(x))=μ(1)= max{μ(x)，μ(c(x))}。若 μ(x)≠μ(1)，因为由定义6知 μ(x)≤μ(1)且μ(c(x))≤ μ(1)，故由 μ(1)=max{μ(x)，μ(c(x))}得μ(c(x))= μ(1)。因此由定义8知μ为X的模糊超MP滤子。

“必要性”：设 μ为 X的模糊超 MP滤子。任取x∈X，因 为 x≤x∨c(x)且 c(x)≤x∨c(x)，故 由 注 1得μ(x)≤μ(x∨c(x))且 μ(c(x))≤μ(x∨c(x))。又由（FUF1）知μ(x)=μ(1)或 μ(c(x))=μ(1)，所以 μ(1)≤μ(x∨c(x))，因此再由定义6便得 μ(x∨c(x))=μ(1)，即（FUF3）成立。

∀x，y∈X，因为x→((x→y)→y)=(x→y)→(x→y)=1且 y→((x→y)→y)=(x→y)→1=1，所以 x≤(x→y)→y且 y≤(x→y)→y，从而 x∨y≤(x→y)→y，因此由 μ的保序性可知 μ(x∨y)≤μ((x→y)→y)。又由 0≤y和FI-（2）得x→0≤x→y，进而(x→y)→y≤(x→0)→y=c(x)→y，因此 μ((x→y)→ y)≤μ(c(x)→ y)，故 μ(x∨y)≤μ(c(x)→ y)。如果 μ(x)=μ(1)，则 μ(x∨y)≤μ(1)=μ(x)≤max{μ(x)，μ(y)}。如果 μ(x)≠μ(1)，则由（FUF1）知 μ(c(x))=μ(1)，所以由定义6可 得 μ(y)≥min{μ(c(x))，μ(c(x)→y)}≥min{μ(1)，μ(c(x)→y)}=μ(c(x)→y)。因此可得 μ(x∨y)≤μ(y)≤max{μ(x)，μ(y)}。故由定义7又知μ是X的模糊素MP滤子。

5 结束语

本文将模糊集的思想和运算方法应用于FI代数的MP滤子理论的研究，引入了FI代数的模糊素MP滤子和模糊超MP滤子概念，并深入讨论了它们的性质特征和相互关系。获得了若干有意义的结论。值得注意的是，诸如MTL代数、R0代数（NM代数）、Heyting代数和MV代数（格蕴涵代数）等都可以看成是FI代数的自然扩张，从而，可以说上述结果是这诸多逻辑代数的共同特征的集中体现。因此，这些结论有助于在把握各种逻辑代数系统的个性特征的同时，也能认识到它们的共性特征和内在联系。

[1] 吴望名.Fuzzy蕴涵代数[J].模糊系统与数学，1990，4（1）：56-64.

[2]李志伟，郑崇友.Heyting代数与Fuzzy蕴涵代数[J].数学杂志，2002，22（2）：237-240.

[3]朱怡权，曹喜望.关于PFI代数与剩余格[J].数学进展，2006，35（2）：223-231.

[4]朱怡权.关于PFI代数的格论性质[J].四川师范大学学报：自然科学版，2007，30（2）：181-184.

[5]代建云，吴洪博.分配的Fuzzy蕴涵代数[J].模糊系统与数学，2008，22（1）：26-32.

[6]刘春辉.Fuzzy蕴涵代数及其拓扑[D].江苏扬州：扬州大学，2008.

[7]刘春辉，徐罗山.Fuzzy蕴涵代数的素MP滤子[J].模糊系统与数学，2011，25（1）：32-37.

[8]裴道武，王三民，杨瑞.模糊蕴涵格理论[J].高校应用数学学报：A辑，2011，26（3）：343-354.

[9]Zadeh L A.Fuzzy sets[J].Information Control，1965，8：338-353.

[10]刘春辉.泛逻辑学中UB代数系统的(∈，∈∨q)-fuzzy滤子[J].计算机工程与应用，2009，45（34）：29-31.

[11]Liu L Z，Li K T.Fuzzy filters of BL-algebras[J].Information Science，2005，173（1/3）：141-154.

[12]Liu L Z，Li K T.Fuzzy implicative and Boolean filters of R0-algebras[J].Information Science，2005，171：61-71.

[13]肖云萍，邹庭荣.泛逻辑学中UB代数系统的滤子与商代数[J].计算机工程与应用，2007，43（35）：90-92.

[14]肖云萍，邹庭荣.泛逻辑学UB代数系统的fuzzy滤子[J].计算机科学与探索，2008，2（2）：212-216.

[15]刘春辉，徐罗山.FI代数的多种Fuzzy滤子[J].模糊系统与数学，2010，24（2）：21-27.

LIU Chunhui

1.Dean’s Office,Chifeng University,Chifeng,Nei Mongol 024001,China
2.College of Mathematics and Statistics,Chifeng University,Chifeng,Nei Mongol 024001,China

It applies the concept of fuzzy sets which introduced by Zadeh to FI-algebras,the notions of fuzzy prime MP filters and fuzzy ultra MP filters of FI-algebras are introduced,their properties and relations are discussed.Some equivalent characterizations of fuzzy prime MP filters in join semi-lattice FI-algebras with certain conditions are given.The fuzzy prime MP filters theorem of join semi-lattice FI-algebras is established.And the sufficient and necessary condition for an fuzzy set to be fuzzy ultra MP filters is obtained.

fuzzy logic;FI-algebra;fuzzy prime MP filter;fuzzy ultra MP filter

将Zadeh提出的模糊集概念应用于FI代数，提出了FI代数的模糊素MP滤子和模糊超MP滤子的概念并研究其性质及相互关系。给出了满足一定条件的并半格FI代数的模糊素MP滤子的若干等价刻画并建立了模糊素MP滤子定理。获得了一个模糊集成为超模糊MP滤子的充要条件。

模糊逻辑；FI代数；模糊素MP滤子；模糊超MP滤子

A

O141.1；O153.1

10.3778/j.issn.1002-8331.1304-0221

LIU Chunhui.Fuzzy prime MP filters and fuzzy ultra MP filters in FI-algebras.Computer Engineering and Applications,2014,50（23）：77-81.

国家自然科学基金（No.10371106，No.60774073）。

刘春辉（1982—），男，讲师，研究领域为非经典数理逻辑、Domain和拓扑学。E-mail：chunhuiliu1982@163.com

2013-04-15

2013-06-03

1002-8331（2014）23-0077-05

CNKI网络优先出版：2013-06-26,http://www.cnki.net/kcms/detail/11.2127.TP.20130626.1542.021.html

◎网络、通信、安全◎