Improving the Performance of Practical Decoy-State Measurement-Device-Independent Quantum Key Distribution with Biased Basis Choice∗

Chun-Hui Zhang(张春辉),Chun-Mei Zhang(张春梅),and Qin Wang(王琴)

Institute of Signal Processing Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China Key Lab of Broadband Wireless Communication and Sensor Network Technology,Nanjing University of Posts and Telecommunications,Ministry of Education,Nanjing 210003,China

AbstractStatistical fluctuations are unavoidable in realistic quantum key distribution(QKD)due to finite-size effect.Based on the four-intensity proposal on measurement-device-independent QKD(MDI-QKD)in[Phys.Rev.A 93(2016)042324],we particularly analyze the scenario that only three intensities are used,namely a three-intensity decoy-state MDI-QKD with biased basis choice.After performing full parameter optimization method,simulations results demonstrate that this scenario can obtain distinct enhancement compared with the conventional unbiased threeintensity decoy-state method,e.g.Xu et al.’s[Phys.Rev.A 89(2014)052333].Furthermore,results also show that it works more efficiently by using HSPS than using WCS at longer transmission distance.

Key words:measurement-device-independent quantum key distribution,statistical fluctuations,biased basis choice

1 Introduction

Based on the laws of quantum mechanics,quantum key distribution(QKD)in principle can possess unconditional security,which permits two legitimate users,usually called Alice and Bob,to share secret keys.[1]To date,many security proofs have been given by established models.[2−10]However,a malicious eavesdropper(Eve)can still make use of loopholes existing in practical QKD devices,launch specific attacks and crack them.[11−14]To solve those problems,various protocols have been put forward,such as the decoy-state method,[15−17]the measurementdevice-independent QKD(MDI-QKD),[18−19]the deviceindependent QKD,[20−21]or the round-robin differential phase shift(RRDPS)protocol,[22−23]etc.Among them,the decoy-state method can close those loopholes caused by imperfect light sources,[24−27]and the MDI-QKD protocol can get rid of all side-channel attacks directed on detecting devices.The combination of the decoy-state method and the MDI-QKD protocol seems to contain the highest level of security within current technology,and thus has been extensively studied.[28−42]

In real-life implementations of decoy-state MDI-QKD,the finite-size effect has to be taken into account due to finite number of pulses used,which significantly depresses the performance of practical QKD.Till today,different approaches have been reported to improve it,[32,34]in which the four-intensity proposal with biased basis choice[34]is the most promising method,significantly improving the performance of MDI-QKD.Here in this paper,we simplified the four-intensity proposal[34]into a biased threeintensity decoy-state MDI-QKD scheme.Moreover,we use two mostly used light sources,e.g.,the weak coherent source(WCS)and the heralded single-photon source(HSPS),as examples and carry out corresponding numerical simulations.After performing full parameter optimization,we demonstrate that,especially with HSPS,this scheme can achieve substantial improvement in both the key generation rate and the secure transmission distance compared with former three-intensity decoy-state MDIQKD.[32]

The article is organized as follows: First,threeintensity decoy-state MDI-QKD with biased basis choice is introduced in Sec.2;Second,corresponding numerical simulations are carried out in Sec.3;Finally,discussions and conclusions are given in Sec.4.

2 The Biased Three-Intensity Decoy-State MDI-QKD

Here,the three-intensity decoy-state method with biased basis choice in MDI-QKD is described as follows:

(i)Alice(Bob)randomly prepares signal state ρµin Z,and X bases with certain probabilities.

(ii)Alice(Bob)prepares decoy state ρvonly in X basis.

(iii)When preparing vacuum state ρo,Alice(Bob)does not choose any basis.

It is different from the normal three-intensity decoystate MDI-QKD protocol,[43]such asXu etal.’s method,[32]as shown in Table 1.In this scheme,the redundancy on preparing states in Z basis for the decoy states is removed.

Table 1 The difference on preparing states between normal 3-intensity decoy-state method and ours in MDI-QKD.The “-” here denotes that Alice(Bob)does not need to choose X basis or Z basis for vacuum state.

In a three-intensity decoy-state MDI-QKD protocol,Alice and Bob individually prepare their light pulses into three different states,i.e.,the vacuum state(ρo=|0⟩⟨0|),the decoy state(ρv)and the signal state(ρµ).In the photon-number space,the vacuum,decoy and signal states of Alice and Bob can be written as

where|n⟩is an n-photon state;the subscript A or B each denotes Alice or Bob;corresponds to the photonnumber distribution of source lA(rB)at Alice’s(Bob’s)side,(l,r=o,v,µ).For any light sources with convex photon-number distribution functions,,and for n>2,they satisfy the condition:[36]

When Alice sends pulses with state ρlAand Bob sends pulses with state ρrB,the average counting rate(Slr)and quantum-bit errors(Tlr=:SlrElr)at the untrustworthy third party(UTP)’s side can be expressed as:

where Yjkand ejkeach denotes the yield and the error rate when Alice sends a j-photon state and Bob sends a k-photon state,Elrcorresponds to the average quantumbit error-rate(QBER),and the notation lr here indicates the two-pulse source when Alice uses source lAand Bob uses source rBto generate a pulse pair.

Evidently,it is hard to give precise estimation for the yield of two-single-photon pulses in Z basis()by employing only the observed data in Z basis,since no decoy pulses have been prepared in Z basis.Interestingly,Ref.[34]has provided a theorem:The yield of two-single-photon pulses in all bases(X and Z)can be tightly lower bounded by using the observed data in the X basis.It has also given a detailed proof for this theorem.Note that Ref.[34]implements four-intensity decoy states,while we need only three different intensities in the simplified scheme.It can not only simplify the complexity of the QKD system,but also reduce the cost of random numbers by using three-intensity decoy-states instead of using four-intensity decoy states in practical QKD system.

To avoid redundancy,hereafter,we just borrow the conclusive result from Ref.[34]and use the observed data in X basis to estimate the lower bound of.Then we can obtain:[31−32]

where

The phase- flip error-rate of the two-single-photon pulses in Z basis can be upper bounded by the quantum-bit errorrate(QBER)of the two-single-photon pulses in X basis,given by:[31−32]

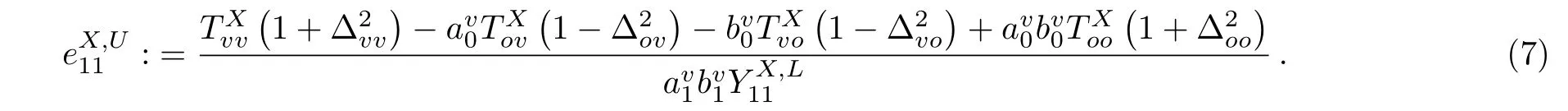
where γ is a constant coefficient depending on the failure probability ε;refers to the number of pulse-pairs when Alice sends state ρlAand Bob sends state ρrBboth in X basis.Here for simplification,we consider the finite-size effect with the standard statistical fluctuations,[28]but it would not in fluence the main conclusion even with other analysis methods,such as the Cherno ffbound method.[44]

With the above formulae,we can calculate the final secure key rate as:[32]

where pµA(pµB)denotes the probability that Alice(Bob)chooses state ρµA(ρµB),and pZ|µA(pZ|µB)corresponds to the probability that Alice(Bob)sends pulses with state ρµA(ρµB)in Z basis;f is the inefficiency of error correction,here we reasonably assume f=1.16;[19,32]H2(p)is the binary Shannon information function,defined as H2(p):=−plog2(p)−(1−p)log2(1−p);andeach denotes the average counting rate and the average QBER in Z basis.

3 Numerical Simulations

In this section,we employ two kinds of light sources,i.e.,the WCS and the HSPS,as examples to investigate the performance of our method and the representative decoy-state MDI-QKD scheme,[32]both carrying out the full parameter optimization method presented in Ref.[32].

As we know,a WCS usually possesses a poissonian photon-number distribution:[28]

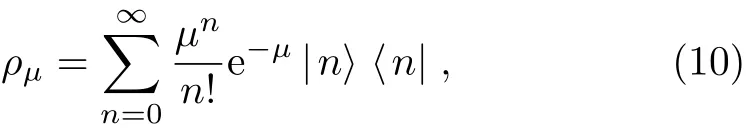
and an HSPS follows a subpossonian photon-number distribution:[30]

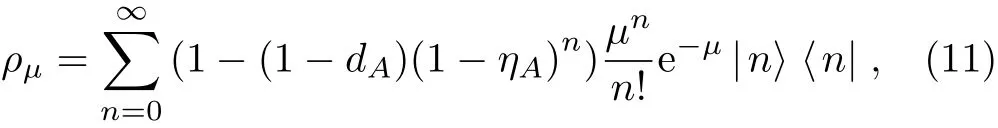
whereµrepresents the average photon number per pulse,|n⟩denotes an n-photon state,ηAand dAeach corresponds to the detection efficiency and dark count rate of Alice(or Bob)’s local detector in HSPS.

To simplify the numerical simulation,here we assume the symmetrical case,i.e.,the UTP is located in the middle between Alice and Bob,and has identical detectors(with the same dark count rates and detection efficiencies).Besides,Alice and Bob possess the same optical and QKD systems.For the case of using HSPS,Alice and Bob own the same local detectors.Then we have,for all n,and pvA=pvB=pv,pµA=pµB=pµ,pZ|µA=pZ|µB=pZ|µ.Moreover,when accounting for statistical fluctuations,we reasonably set the confidence interval as γ=5.3,corresponding to a failure probability of 10−7.[30,32]We use the same experimental parameters as in Ref.[32]in our simulation,as listed in Table 2.

Table 2 The systematic parameters used in our numerical simulations.α represents the loss coefficient of standard commercial single-modefibers;e0denotes the error rate of vacuum pulses;edrefers to the misalignment probability of the whole optical system;ηdand Y0each corresponds to the detection efficiency and the dark count rate of detectors at the UTP’s side; ηAand dAare the detection efficiency and the dark count rate of the commercial silicon detector at Alice(or Bob)’s side when applying HSPS.

In the following,for a fair comparison,we use the same full parameter optimization method presented in Ref.[32],i.e.,the local search algorithm(LSA),for both Xu et al.’s method and our method,which includes the intensities of the signal states(µ)and the decoy states(v),the probabilities of choosing different intensities(pµ,pv)and the probabilities of choosing different bases in corresponding intensities(pX|µ,pX|vin Xu et al.’s method,and pX|µin ours).Corresponding simulation results are displayed out in Figs.1–4.

In order to show the consistence of the scheme with other former work,we calculate the final key generation rate of using this method and Xu et al.’s work[32]when both taking statistical fluctuations into account,while setting the number of pulses with a very large value,e.g.,N=1025.Moreover,we also calculate the key generation rate of using standard three-intensity decoy-state MDI-QKD without considering statistical fluctuations,as shown in Fig.1.We can see from Fig.1(a)that when the number of pulses is very large,e.g.,N=1025,both our method(W2(H2))and Xu et al.’s work(W1(H1))approach very closely to the ideal case of without accounting for statistical fluctuations(W0(H0)).Moreover,in order to illustrate it more clearly,we also display the relative key rate in Fig.1(b).It denotes the ratio of the key rate between using practical three-intensity decoy-state methods and corresponding asymptotic case of using in finite number of pulses,which again verifies the the consistence of our method with Xu et al.’s work.Below we also give analytical explanations on it.

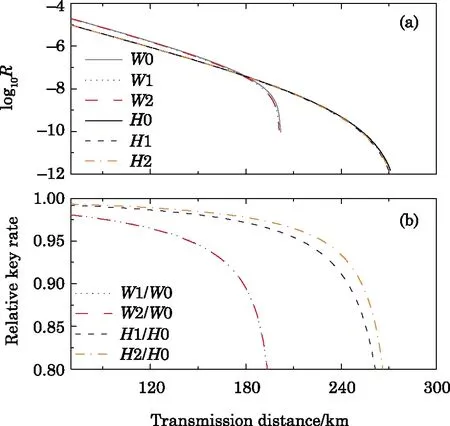
Fig.1 (Color online)Asymptotic comparison of the if nal key generation rate between Xu et al.’s work and our work.(a)The absolute values of the final key rates with logarithm scale:W0(H0)refers to the results of using standard three-intensity decoy-state MDI-QKD with WCS(HSPS)without considering statistical fluctuations;W1(H1)represents the results of employing Xu et al.’s three-intensity decoy-state MDI-QKD with WCS(HSPS)by accounting for statistical fluctuations;W2(H2)corresponds to applying our method with WCS(HSPS)when taking statistical fluctuations into account.(b)The relative values of final key generation rates.We

In the limit N→∞,the density matrices satisfy=,which means the quantum states of twosingle-photon pulses in X basis or Z basis are completely the same.Then,the counting rates of two-single-photon pulses satisfy=.Besides,in Eqs.(4)–(7),→0 and→0.As a result,the key rates of both our method and Xu et al.’s work approach very closely to the ideal case of without accounting for statistical fluctuations.

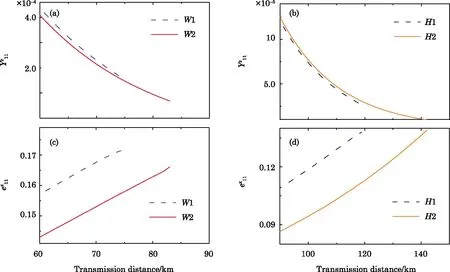
Fig.2 (Color online)Comparisons of the two-single-photon-pulse contributions between Xu et al.’s work and ours.(a)and(c)correspond to the results of using WCS,while(b)and(d)denote using HSPS.W1(H1)refers to implementing Xu et al.’s three-intensity decoy-state method,and W2(H2)represents applying our method.Here we reasonably set the number of pulses as N=1011.

In Fig.2,we do comparison on the contributions of two-single-photon pulses,i.e.,its conditional counting rate()and the phase- flip error-rate()between Xu et al.’s work[32]and our method using either WCS or HSPS.Here the data size of the pulse number is reasonably set as N=1011.We can see from Figs.2(a)and 2(b)that,both methods present comparable values of.While for the values of,our method presents much lower values than the former as shown in Figs.2(c)and 2(d).Obviously,our method can achieve more precise estimation forcompared with Xu et al.’s work.Because we have removed the redundancy on preparing states in Z basis for the decoy states and without in fluencing the security.Then there will be more data in X basis to be applied to estimate the value of.Correspondingly,our method will su ff er less finite-size effect and can thus show significant enhancement in both the key generation rate and the secure transmission distance compared with Xu et al.’s work.[32]

Figure 3 shows comparisons of the final key generation rate between our method and Xu et al.’s method using either WCS or HSPS and considering different data sizes.Figures 3(a)and 3(b)refer to the absolute key generation rates with logarithmic coordinate,while Figs.3(c)and 3(d)correspond to the relative values with linear scale.Obviously,our method can drastically improve the key generation rate compared with Xu et al.’s work using either WCS or HSPS.And the smaller data size,the more distinct enhancement we can achieve.Moreover,our method applying HSPS works more efficiently than using WCS.For example,at the data size of N=1011and at the distance of 100 km,there is no key can be generated by using WCS,while a relative high key rate can still be obtained by applying HSPS.Moreover,when both using HSPS,we can get more than 40%enhancement in the key generation rate at the data size of N=1012,and 300%enhancement at N=1011when compared with Xu et al.’s method.Those enhancements can be attributed to two inherent merits of HSPS:(i)The neglectable dark count rate;(ii)The significantly lower probability for events with two photons presenting on the same side of the beamsplitter during Bell-projection measurements.

Moreover,to demonstrate that the merits of the present scheme will not change even when the Cherno ffbound[44]is applied in analyzing statistical fluctuations,we plot Fig.4 by implementing the Cherno ffbound method on the above two schemes.Here the data size is reasonably set N=1011.The absolute values and the relative values are respectively shown in Figs.4(a)and 4(b).Obviously,we can find the same trends as in Fig.3.

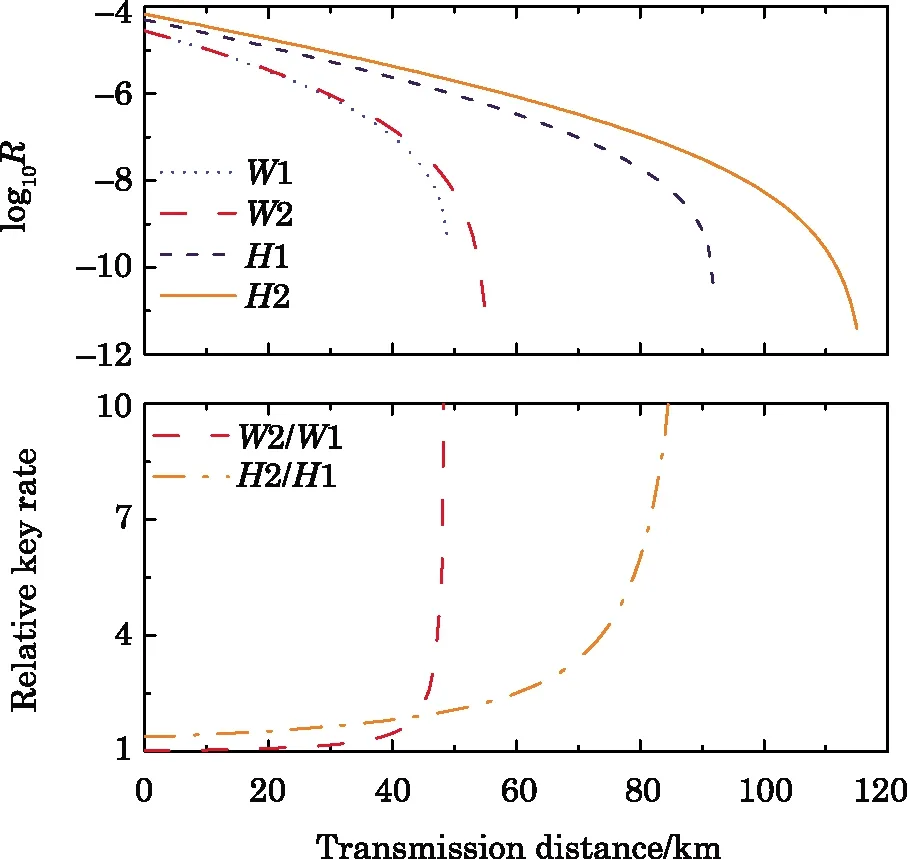
Fig.4 (Color online)Comparisons of the final key generation rate between Xu et al.’s method and ours by applying the Cherno ffbound analysis.(a)displays the absolute key generation rates with logarithmic coordinate,and(b)exhibits the relative values with linear scale.W1(H1)represents the results of Xu et al.’s method,and W2(H2)denotes ours.Here the number of pulses is reasonably set at N=1011.

4 Conclusions

In conclusion,we have applied the idea of biased basis choice in Ref.[34]into the three-intensity decoy-state MDI-QKD scheme and carried out full parameter optimization on it.Compared with Xu et al.’s three-intensity scheme,[34]here the main difference is that the decoy pulses only prepared in X basis,which leads to more data in X basis for estimating the quantum-bit errorrate of two-single-photon pulses accurately.Therefore,this method su ff ers less finite-size effect during parameter estimations and can achieve better performance in the key distillation.Furthermore,numerical simulation results show that this method works more efficiently by using HSPS than using WCS at longer transmission distance.This attributes to the negligible dark count rate in HSPS,and dramatically lower probability for events with two photons presenting on the same side of the beamsplitter in HSPS than in WCS.In addition,this method can be easily realized with current technology,and thus looks very promising in the implementation of the quantum communication.