S变换在中性点不接地系统接地选线中的应用

陶维青 曹红光 余南华 李 林 殷少戈 鲍晓菲

(1.合肥工业大学电气与自动化工程学院，合肥 230009；2.广东电网公司电力科学研究院，广州 510080；3.安徽科大智能电网技术有限公司，合肥 230060)

我国的中低压配电网主要采用小电流接地系统，其中3～10kV电网主要采用中性点不接地系统，35～60kV电网主要采用中性点经消弧线圈接地系统。当发生单相接地故障时，故障电流很小，线电压仍保持平衡，可继续供电一段时间，一般不超过1～2h，但是非故障线路的相电压升高，会对线路的绝缘栅产生影响。

近年来，许多学者就故障选线问题做了大量的研究，提出了基于稳态量和暂态量[1,2]的故障选线方法。如早期的群体比幅、群体比相、群体比幅比相法及首半波法等，但是由于小电流接地系统发生单相接地故障时，故障电流很小，特征不明显，随着变电站的出线越来越多，故障电流与非故障电流的判别越来越困难，这些传统的选线方法在实际运行中总体效果并不理想。由于配电网单相接地故障后会产生丰富的暂态信号，且暂态量的获取不需要太高的采样频率，加之现代信号分析方法的发展(如小波变换等)，基于暂态量的选线方法得到了学者们的广泛关注。但故障选线的准确性和可靠性还远不能满足工程需要，仍需进行理论研究和工程实践。

S变换是在连续小波和短时傅里叶变换的基础上发展来的一种时频分析方法。它集中了短时傅里叶变换和小波变换的优点，与短时傅里叶变换相比，它克服了窗口高度与宽度固定不变的缺陷；与小波变换相比，它在高频部分的分解更加细致。信号经S变换后得到一个复时频矩阵，包含有信号幅值及相位等随时间、频率的分布信息，为提取信号特征提供了基础信息。笔者首先探讨了故障合闸角(故障发生时刻对应相电压的相角大小)、过渡电阻、线路长度及出线个数等因素对传统的一些选线方法的影响。根据传统选线方法的不足，提出了基于S变换故障选线方法。笔者以特征频率下各线路的暂态能量为特征，然后按由大到小排列，提取前3个暂态能量值，以最大的值与后两个值和的关系为判据，判断故障线路，从而达到故障选线的要求，并着重分析了当系统含有噪声干扰，非线性负载及故障合闸角等因素变化时此选线方法的准确性与可靠性。

1 传统选线方法缺点分析①

当某条线路发生单相接地故障时，母线线路的零序电压和各线路零序电流波形如图1所示。从图1中可以看出，在发生单相接地故障后，整个系统出现零序电压和零序电流。各线路产生的零序电流的暂态过程中，故障线路和非故障线路的零序电流均存在高频振荡。故障线路的零序电流幅值较大，且与非故障线路的零序电流的方向相反。

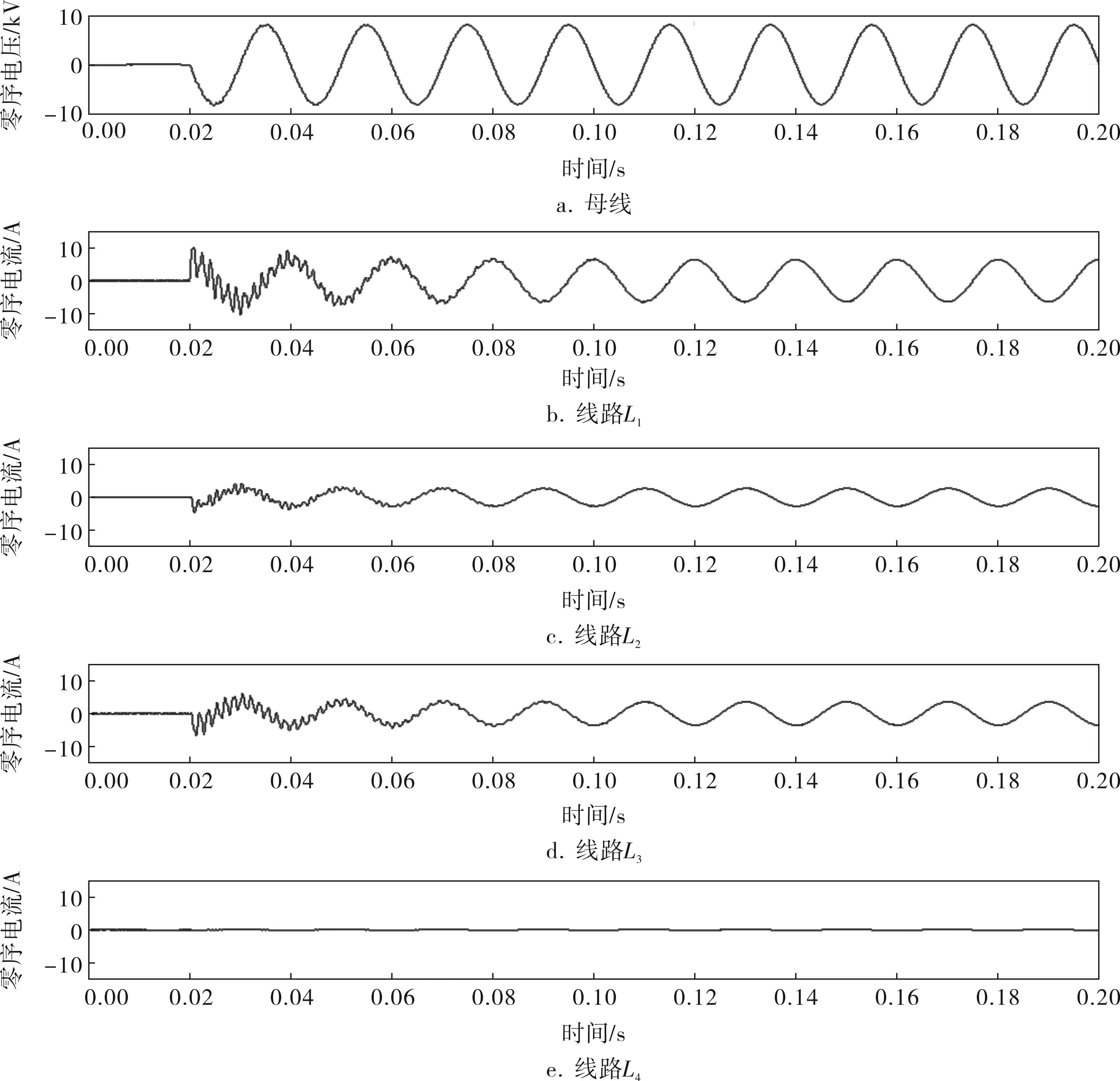
图1 母线零序电压和4条线路零序电流

当过渡电阻和其他因素一定时，随着故障合闸角的增加，故障线路零序电流波形如图2所示。

图2 线路1在故障合闸角为0、90、180°下的零序电流

从图2中可以看出在故障合闸角为90°时，由于相电压在峰值附近，发生单相接地故障时，电容放电，故障线路产生的暂态零序电流幅值较合闸角为0°时大几倍，暂态过程比较强烈且产生的振荡频率较高。故障合闸角为180°时的零序电流的相位与合闸角为0°时的相位相反，但幅值没变。

当故障合闸角等因素一定时，随着过渡电阻的增加，故障线路零序电流波形如图3所示。从图3中可以看出，随着过渡电阻增加，零序电流中含有的高频暂态分量的主谐振频率变高，但不影响工频零序电流的稳态幅值。

图3 不同过渡电阻下的线路1零序电流

1.1 稳态分析

不同长度下提取的稳态工频(50Hz)零序电流的幅值见表1。由表1可知当某条非故障线路的长度很大时，故障线路和非故障线路的工频零序电流幅值的大小很接近。因此，采用提取工频零序电流幅值作为故障特征的方法受到线路长度的影响，当某条非故障线路的出线长度很长时，故障选线过程中可能产生误选。

表1 不同长度下各线路工频零序电流幅值和相位

从由表1可知，故障线路的相位与其他非故障线路的相位相反。但是结合图1知，当出线个数较少，线路较短时，如线路4的长度很小时，产生的零序电流的幅值很小，不易于检测，给选线带来困难。

1.2 暂态分析

采用首半波法进行故障选线的原理是通过比较故障起始后暂态零序电压半波波形与暂态零序电流半波波形的幅值和极性，故障线路和非故障线路的首半波幅值和极性均不相同；极性相同则判为健全线路。结合图2知，当故障合闸角发生在90°附近时，极性关系成立的时间很短，很难被检测出来。所以此方法受到故障合闸角的影响。

根据传统的一些稳态，暂态选线方法的不足，下面提出了一种特征频率下S变换暂态能量的故障选线方法。

2 基于特征频率的S变换暂态能量法

S变换集合了短时傅里叶变换和小波变换的优点，它具备时频局部化特征，并能有效地收集到在每一个频率点处的信号特征。信号x(t)的S变换S(τ,f)定义为：

(1)

(2)

式中f——频率；

ω(τ-t,f)——高斯窗口；

τ——控制高斯窗口在时间轴t的位置参数。

根据文献[3]，一个故障配电网络可分为由三相电压源、馈电线路与负载组成的无故障正常网络和由当故障发生时产生的额外电压源与在故障点处的馈线组成的故障分量网络。因此，故障点的零序能量函数定义为[4]:

(3)

式中N——馈电线路上监测装置的总数；

u0i(t)、i0i(t)——对应的是第i个监测装置监测到的零序电压和零序电流；

Wi(t)——故障发生时第i个监测装置的零序能量函数。

由于用各馈线的故障分量的能量进行比较，而每条线路监测装置监测的零序电压均为母线零序电压，则分析中可略去零序电压。利用S变换提取信号各个频率点的特征，可定义各线路在频率下的暂态能量为：

(4)

式中m，n——S模矩阵的列数和行数，且行对应频率，列对应采样时间点；

Si(m,n)——第i条线路的S模矩阵。

对所有线路在各频率的暂态能量分别求和，可得到在各个频率点处的系统暂态能量和为:

(5)

发生故障时，尽管各条线路的暂态能量存在差异，但是，由于故障线路的暂态能量起着主导作用，因此，系统暂态能量的最大值所对应的频率将与故障线路能量最集中的频率一致，频率下的故障能量特征亦最明显。定义系统暂态能量和最大值对应的频率为故障特征频率fk，在此频率上，故障线路的暂态能量将大于各健全线路的暂态能量，由此可构造故障选线判据。算法的步骤为：

a. 对采样获得的故障后T/4内各条线路的零序电流i0i(t)进行S变换，计算模矩阵Si。

b. 利用式(4)计算各条线路零序电流在各个频率点的暂态能量。

c. 利用式(5)对所有线路在各个频率点处的暂态能量分别求和，可得到在各个频率点处的系统暂态能量和Wn，根据Wn的最大值确定特征频率fk。

d. 提取各条线路在特征频率上的暂态能量Wi，k,i=1,2,…,N。

e. 选出各线路1/4周期特征频率处暂态能量中前三个最大值，按由大到小的顺序排列为Wp_k,Wq_k,Wr_k, 当满足|Wp_k|≤|Wq_k|+|Wr_k|时，判定为母线故障；否则，判定暂态能量最大的线路p为故障线路。

假设当线路1发生故障时，根据上面的步骤，提取各线路零序电流故障后1/4周波的数据，对其进行S变换并求模，得到了一个51×100的S模矩阵。按上述步骤提取各条线路在各个频率点处的暂态能量分布如图4所示。可以看出，1/4周波的零序电流经S变换将暂态能量按51个频率点进行划分，n=1对应信号的直流分量，频率为0,相邻之间的频率间隔定义为fs/N=200Hz。

图4 各线路在各频率点的暂态能量分布

对所有线路在各频率点处的暂态能量分别求和，得到在各个频率点处的系统暂态能量和如图5a所示。可以看出，在n=4的频率点上的值最大，则特征频率为fk=(fs/N)×(n-1)=600Hz。提取特征频率上各条线路的暂态能量，如图5b所示，可以看出，线路1在特征频率下的暂态能量最大，其次是线路3、线路2、线路4。

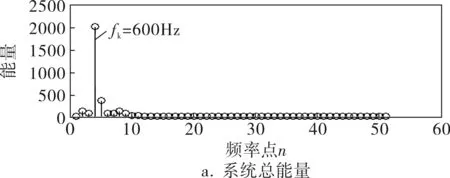
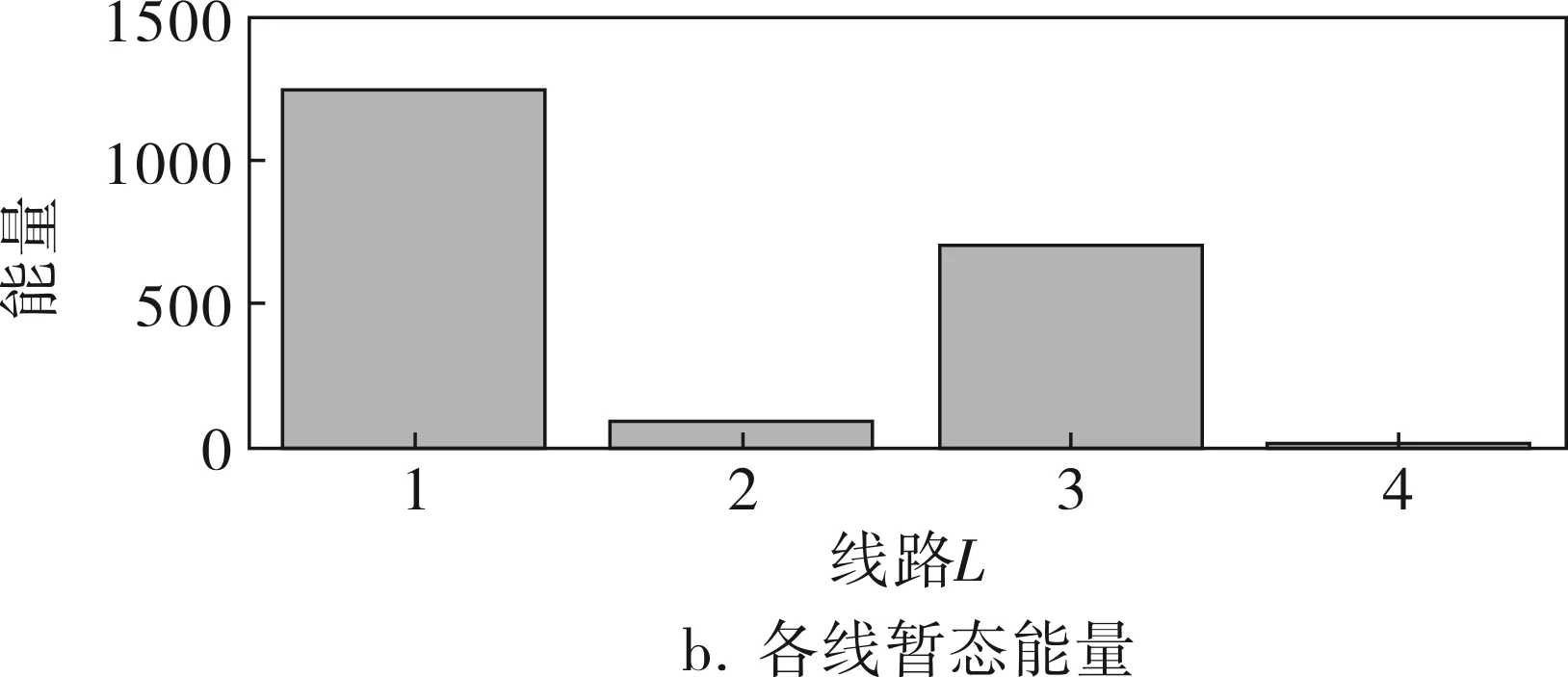
图5 系统总能量及特征频率下各线暂态能量

3 实验仿真及数据分析

按图6所示中性点不接地系统的示意图建立仿真模型。图6是含有4条出线的10kV配电网，接地方式为中性点不接地，线路采用架空线路，线路长度分别为10、15、20、1km。各线路的正序阻抗、感抗、容抗均为0.012 7Ω/km、0.933mH/km、0.12μF/km;零序阻抗、感抗、容抗均为0.368Ω/km、4.126mH/km、 0.07μF/km。假设故障发生在0.02s,过渡电阻为1MΩ。

当故障合闸角改变、线路的长度变化或过渡电阻变化，得到的各线路在特征频率下的暂态能量见表2。

图6 中性点不接地系统的示意图

Liθ(°)RfΩLen/km[L1 L2 L3 L4]noisefkHz暂态能量[W1,W2,W3,W4]选线结果1030[10 15 20 1]-600[601.53,37.19,330.42,0.09]正确9030[10 15 20 1]-600[7.02×104,3.80×103,4.09×104,7.71]正确0500[10 15 20 1]-600[1 199.00,70.85,671.40,0.15]正确030[10 200 20 1]-400[9 308.00,5902.10,359.89,0.49]正确030[10 15 20 1]均值为0,方差为1600[564.53,41.27,327.32,0.97]正确2030[10 15 20 1]-600[9.41,413.31,289.94,0.07]正确

注：fk——对应特征频率；Len——线路长度；Li——第i条线路故障； noise——一个高斯白噪声；Rf——过渡电阻；θ——故障合闸角。

在实际现场，采集到的信号一般会存在很多干扰。限于篇幅的限制，笔者仅对在系统中加入了一个均值为0、方差为1的高斯白噪声信号进行选线验证。

当加入噪声后，得到的线路1的零序电流波形如图7所示。

图7 加入白噪声后线路1的零序电流

通过S变换得到的各线路在各个频率点处的暂态能量和，和特征频率下各线路暂态能量的波形如图8所示。

图8 系统总能量及特征频率下各线暂态能量

由图8可得，特征频率为600Hz，特征频率下各线路的暂态能量分别为W1=1146.20，W2=89.67，W3=680.29，W4=4.32。分析可知,W1>W2+W3，故可判定线路1故障。

4 结束语

当发生单相接地故障时，暂态零序电流受故障合闸角、过渡电阻、线路长度及出线个数等因素的影响。即随着故障合闸角的的增加，暂态零序电流变大，但不影响零序电流的稳态幅值。随过渡电阻的变化，暂态零序电流中高频振荡分量所占比重不同。传统的一些选线方法受到这些因素的影响，即通过提取工频零序电流幅值的方法作为故障特征，受到线路长度的影响，当某条线路的线路长度很长时，仅提取该特征，容易产生误选。当故障线路的长度很短且出线个数很少时，产生的零序电流很小，采用群体比幅比相的方法不易于检测，暂态分析中的首半波法受故障合闸角的影响。

而基于特征频率下S变换的暂态能量法进行故障选线的方法，不仅能够判别支线故障，也能判别母线故障，且选线效果显著。而且，此方法不受系统噪声干扰、故障合闸角、过渡电阻及线路长度等因素的影响。下一步的工作将考虑非线性负载谐波源以及结合新能源(如风能)等对故障选线的影响；且利用S变换和傅里叶变换相结合的分析方法分别对信号进行暂态和稳态分析，以期望达到有效的选线目的。