基于贝叶斯理论的逐次迭代非线性AVA反演方法

代荣获，张繁昌，刘汉卿，李灿灿

中国石油大学(华东)地球科学与技术学院，山东 青岛 266580

基于贝叶斯理论的逐次迭代非线性AVA反演方法

代荣获，张繁昌，刘汉卿，李灿灿

中国石油大学(华东)地球科学与技术学院，山东 青岛 266580

常规AVA三参数反演方法均基于横波速度与纵波速度之比γ为常数这一假设条件，且常被近似地取为0.5。然而在许多情况下γ并不为常数，而是在横向与纵向都渐变。若一概假定γ等于0.5，反演出的岩性参数势必要偏离真实值，因此有必要合理地选择γ。笔者基于贝叶斯理论，提出逐次迭代非线性AVA的反演方法。该方法把γ看成横向与纵向都渐变的反演初始背景，通过给定初始模型计算初始背景γ，并采用逐次迭代的策略求解该反演问题,解决了关于γ的选取问题以及由于引入变γ值而带来的非线性问题，提高了AVA三参数反演结果的精确度。

AVA反演；非线性；变纵横波速度比；逐次迭代；贝叶斯理论

0 引言

基于叠前地震道集的反演技术在油田勘探和开发中起着越来越重要的作用，其理论基础是描述平面波在水平界面上反射与透射的Zoeppritz方程[1]。基于Zoeppritz方程近似公式，常用的叠前地震反演分为两种，一种是弹性阻抗反演[2-3]，另一种是AVA(amplitude variation with incident angle)三参数反演[4-5]。杨培杰等[6]利用Fatti近似式[7]，发展了AVA三参数反演技术，反演出比较稳定的纵波阻抗、横波阻抗和密度岩性参数。由于泊松比是叠前地震反演的重要参数,桂金咏等[8]提出直接用纵波速度、泊松比和密度表示的反射系数近似式。利用该公式可以直接提取泊松比，因此笔者在反演中采用该近似式。

上述叠前反演方法均基于γ(横波速度与纵波速度之比，vS/vP)为常数这一假设条件，把非线性的AVA反演问题线性化，从而提高反演的稳定性与可操作性。然而在实际中，很多情况下γ并不为常数，而是在横向与纵向都逐渐变化。李爱山[9]详细讨论了弹性阻抗方程中γ的选取问题，指出不同的AVA模型具有不同的最优γ值；Alemie[10]详细讨论了γ对AVA反演的影响，指出错误的γ值会导致反演结果偏离真实值，特别是在上下地层岩性参数变化比较大时，会出现较大误差。文中从四类基本AVA模型出发，讨论不同AVA类型在假设γ取0.50时，纵波反射系数的变化情况，并与Zoeppritz方程计算出的反射系数比较，说明若一概假定γ为0.50，反演出的岩性参数势必要偏离真实值，有必要合理地选择γ。为此，笔者提出逐次迭代非线性AVA反演方法:该方法将γ看作随横向与纵向变化的反演初始背景，通过给定初始模型计算初始γ，得到初始背景下的岩性参数；然后采用逐次迭代的反演策略，即将上次迭代的结果作为下次迭代反演的初始模型，重新构建背景γ；如此逐次迭代下去，直到满足停止迭代条件为止，从而使得反演结果充分逼近真实值，并将最后一次迭代结果作为最终反演结果。

1 方法原理

1.1 线性AVA反演

AVA反演大多基于Aki和Richards[11]给出的纵波反射系数近似方程，桂金咏等[8]对该公式重新进行了整理，推导出能够直接反演泊松比的反射系数近似式，可写成如下形式:

(1)

其中：

b(γ,θ)=2(γ2-1)sin2θ；

由式(1)可知，γ、RP、Rσ、Rρ都是待求的未知目标参数。由于γ的存在，式(1)是典型的非线性方程。解这类方程的基本思想是采用非线性反演方法，即给定初始模型，通过不断迭代修正模型参数达到最终反演岩性参数的目的；但这种方法在求解过程中需要求解雅克比矩阵和汉森矩阵，在实际应用中很不方便。因此，最常见的AVA反演是采用线性方法，其基本思想是对γ做出某种近似假设，比如通常取为0.50，这样式(1)所描述的非线性问题被线性化，然后采用最小二乘算法进行反演，达到最终反演岩性参数的目的。

1.2 线性AVA反演的不足

由上节讨论可知，当今应用最广泛的AVA反演方法是线性反演法，其基本假设条件是γ取0.50。然而在实际中，许多情况下γ并不为常数，而是在横向与纵向都渐变。本节从四类典型AVA模型出发，讨论不同模型在假设γ取常数时的纵波反射系数变化情况。

Rutherford和Williams[12]把含气砂岩的AVA异常分为3类。1997年Castagna和Swan[13]在此基础上扩展为4类AVA异常，各类模型的介质参数见表1。对每类AVA模型分别用Zoeppritz方程、γ由真实模型得到、假定γ取0.50和假定γ取0.58(即介质是泊松体)4种方法计算出纵波反射系数曲线，结果如图1所示。从图1中可以看出：对于第一类与第二类AVA模型，γ为常数时计算出的纵波反射系数与用Zoeppritz方程计算出的纵波反射系数之间误差较小；但是对于第三类与第四类AVA模型，γ为常数计算出的反射系数与用Zoeppritz方程计算出的反射系数之间的误差比较明显，在入射角大于20°之后越来越大，特别是在25°之后，误差已不可忽略。在这种情况下，γ取为0.50这一假设条件已不再成立，反演出的岩性参数势必会出现较大误差。

1.3 逐次迭代非线性AVA反演法

由贝叶斯反演理论可知，在给定数据空间d与反射系数模型空间r的似然函数及先验信息时，反射系数的后验概率分布函数为[14]

式中：p(r|d)表示反射系数的后验概率；p(r)表示反射系数先验信息；p(d|r)表示似然函数。

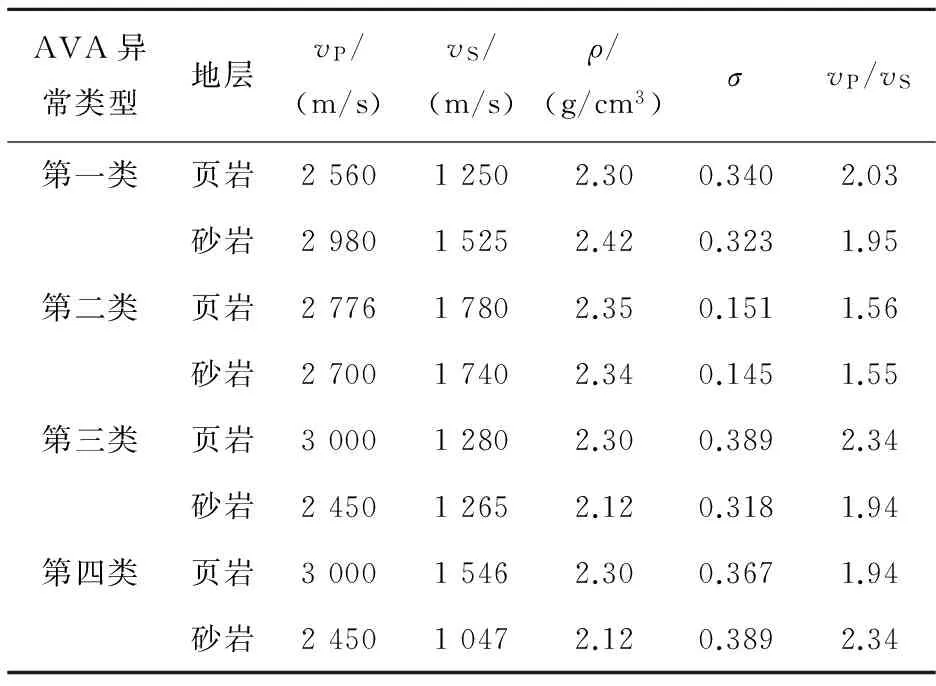
表1 四类AVA界面模型

假设地震数据噪声的均值与均方差分别为0和σS，且服从高斯分布，并采用柯西先验准则[15]，基于贝叶斯理论并以反射系数近似式(1)为正演算子，可建立AVA反演的目标泛函：

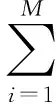
(3)

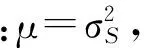
在叠前地震反演中，为合理地选取γ，通常把γ作为一个待反演的未知参数加到反演中，采用非线性方法求解。但这种方法在求解过程中需要求解雅克比矩阵和汉森矩阵，反演结果很不稳定。为此，笔者提出逐次迭代的非线性AVA反演方法，以合理解决该问题，具体方法如下。

把γ看作在横向与纵向都渐变的反演初始背景，而待反演的岩性参数则是背景上的扰动。步骤如下：1)结合基于模型反演方法的思想，通过给定初始模型计算初始γ，并代入到似然函数中，从而把非线性的AVA反演目标函数线性化；2)利用最小二乘算法，获得初始背景下的岩性参数；3)把上次迭代得到的结果作为下次迭代的初始背景模型，重新构建γ，并重新加入到似然函数中，然后利用最小二乘算法得到新背景下的反演结果；4)如此逐次迭代下去，直到第n次迭代的结果与第n+1次的结果充分相关，则停止迭代。反演结果充分逼近真实值，并将最后一次迭代结果作为最终反演结果，这种反演策略称为逐次迭代方法。

2 应用效果分析

2.1 逐次迭代反演与常规反演结果对比

a.第一类；b.第二类；c.第三类；d.第四类。图1 四类AVA模型反射系数曲线Fig.1 Reflection coefficient curves for four classes AVA model

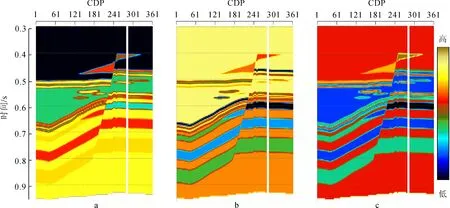
a.纵波速度；b.泊松比；c.密度。图2 二维地层模型Fig.2 2D geological model

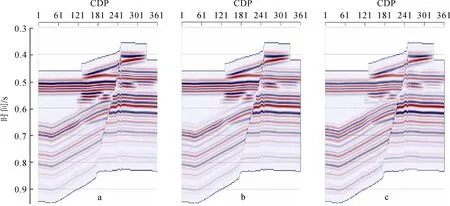
a.5°；b.15°；c.25°。图3 不同入射角地震剖面Fig. 3 Seismic sections of different incident angles

为了说明逐次迭代非线性AVA反演的可行性以及相对于常规AVA反演的优势，采用如图2所示的二维模型进行验证。由Zoeppritz方程正演生成该模型的叠前AVA地震剖面，不同入射角的剖面如图3所示。首先利用图3的地震数据进行常规AVA三参数反演；然后以真实模型平滑100次后的平滑模型作为初始值，利用图3的地震数据进行逐次迭代非线性AVA反演。为分析逐次迭代非线性反演的优势，抽取如模型(图2)中白色线所示的单道进行对比分析，结果如图4所示。对比两种反演结果可以看出，逐次迭代非线性AVA反演结果与真实模型吻合程度更高，特别是在上下地层岩性参数变化比较剧烈的情况时，有着更加明显的优势。分别计算两种反演结果与真实模型的相关系数，结果如表2所示。可以看出，不论是纵波速度还是泊松比与密度，逐次迭代非线性反演结果都具有更高的相关性。以上对比可以说明，逐次迭代AVA反演能够得到与真实模型更加匹配的反演结果。

2.2 逐次迭代反演抗噪性分析

为说明逐次迭代非线性AVA反演的稳定性和优良抗噪性，采用一维单井模型进行测试。由Zoeppritz方程正演生成模型的叠前地震记录，结果如图5a所示；然后对无噪声的合成地震数据加入不同程度的高斯随机噪声，结果如图5b--d所示。

表2 常规反演结果和逐次迭代反演结果与真实模型的相关系数

Table 2 Correlations comparison of conventional inversion with new method

vP相关系数σ相关系数ρ相关系数常规反演结果0.9060450.8892340.839998逐次迭代反演结果0.9863770.9582760.931101

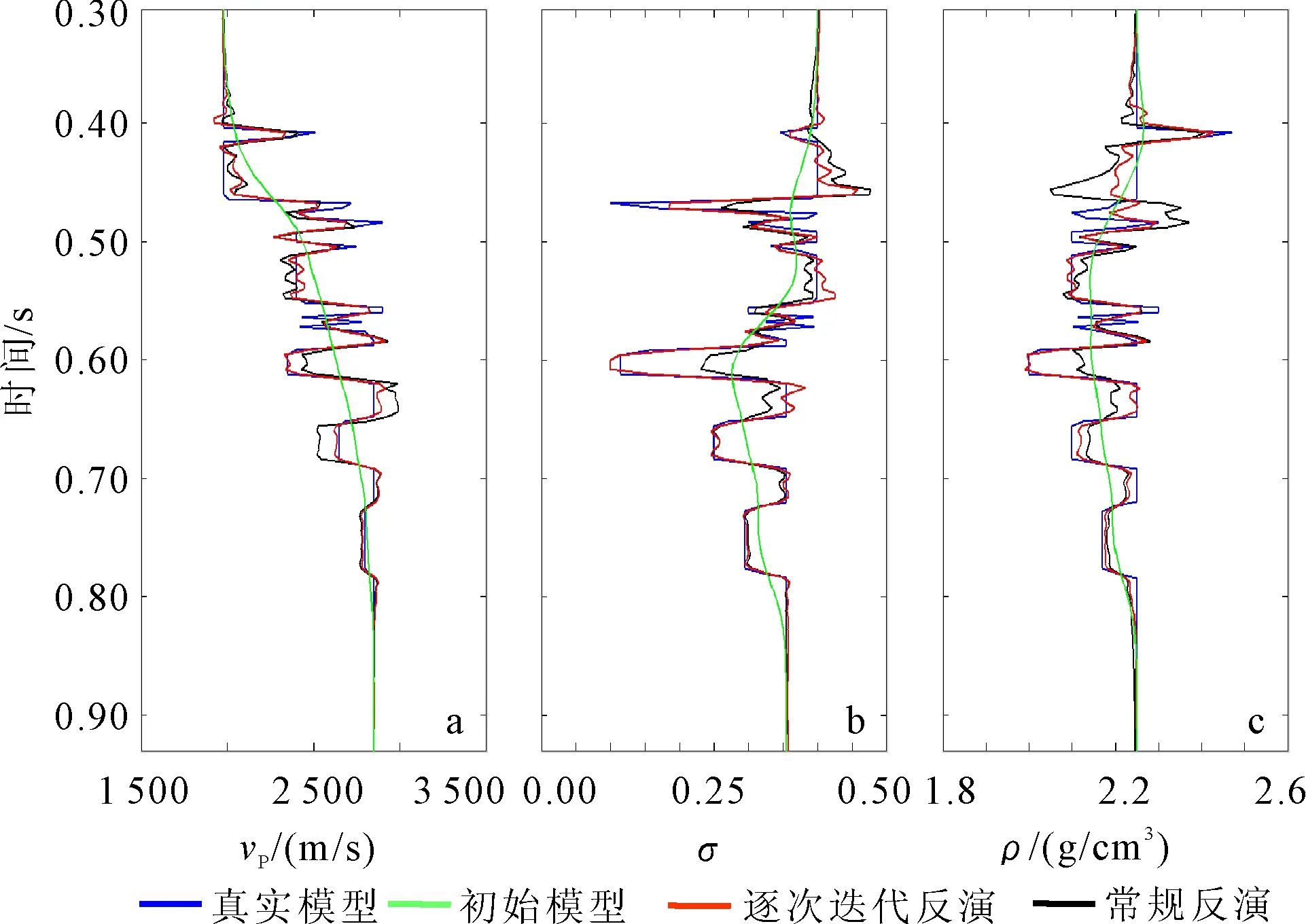
a.纵波速度；b.泊松比；c.密度。图4 常规反演结果与逐次迭代反演结果对比Fig.4 Inversion results comparison of conventional method with the proposed method

a.无噪声；b.信噪比为10∶1；c.信噪比为5∶1；d.信噪比为1∶1。图5 不同信噪比的一维单井模型合成地震道集Fig.5 Synthetic seismic gathers with different S/N for 1D well-log model

以图6中的绿色曲线作为初始值，分别对图5a所示的地震数据进行逐次迭代反演和常规反演，反演结果如图6中的红色曲线和黑色曲线所示。从图6中可以看出：在初始模型非常平滑的条件下，两种反演方法得到的纵波速度、泊松比和密度与真实模型(图6中的蓝色曲线)都基本吻合；但在上下地层岩性参数变化较大时，逐次迭代反演的吻合程度更高。

为进一步验证逐次迭代反演方法的抗噪性，对含噪声的地震数据进行逐次迭代反演与常规反演，反演结果如图7、图8与图9所示。从图7--9中可以看出：当上下地层岩性参数变化比较剧烈时，逐次迭代反演结果与真实模型匹配度更高(如0.15～0.20 s的反演结果)；随着地震数据噪音的加大，在信噪比为1∶1时，两种反演结果都难以得到合理的密度反演结果，但是逐次迭代反演结果仍比常规反演结果更接近真实模型。

a.纵波速度；b.泊松比；c.密度。图6 无噪声时一维模型反演结果Fig.6 Inversion results with free noise for 1D model

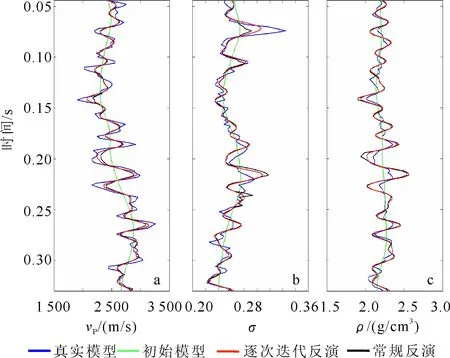
a.纵波速度; b.泊松比; c.密度。图7 信噪比为10∶1时一维模型反演结果Fig.7 Inversion results with S/N equal to 10∶1 for 1D model

a.纵波速度; b.泊松比; c.密度。图8 信噪比为5∶1时一维模型反演结果Fig.8 Inversion results with S/N equal to 5∶1 for 1D model

a.纵波速度; b.泊松比; c.密度。图9 信噪比为1∶1时一维模型反演结果Fig.9 Inversion results with S/N equal to 1∶1 for 1D model

3 结论

1)常规的叠前地震反演，随着入射角的增大，常数背景γ假设条件不再成立，依赖于该假设反演求得的岩性参数势必会出现较大的误差。

2)在常规AVA三参数同步反演的基础上，基于贝叶斯理论，提出了逐次迭代非线性AVA反演方法，克服了常规反演的不足，使得反演结果更充分地逼近真实值。

3)从应用效果及抗噪性能测试结果来看，逐次迭代非线性AVA反演方法突破了常规AVA反演基于常γ值这一假设条件的限制，提高了叠前AVA三参数反演结果的精确度；同时，该方法还具有良好的稳定性和抗噪性。

[1] Zoeppritz K, Erdbebnenwellen V. On the Reflection and Penetration of Seismic Waves Through Unstable Layers[J]. Göttinger Nachrichten, 1919, 1:66-84.

[2] Connolly P. Elastic Impedance[J]. The Leading Edge, 1999, 18(4):438-452.

[3] 李超，印兴耀，张广智，等. 基于入射角的AVO近似弹性阻抗方程及反演[J]. 吉林大学学报：地球科学版，2013, 43(5):1663-1671. Li Chao, Yin Xinyao, Zhang Guangzhi, et al. Elastic Impedance Equation Based on the Incident-Angle AVO Approximation and Inversion[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(5): 1663-1671.

[4] Hampson D P, Russell B H, Brad P B. Simultaneous Inversion of Pre-Stack Seismic Data[C]//75th Annual International Meeting. Houston: SEG, 2005:1633-1638.

[5] 刘财，刘宇巍，冯暄，等. 基于方位相交的纵波AVA数据运用SVD反演HTI介质裂缝密度[J]. 吉林大学学报：地球科学版，2013, 43(5):1655-1662. Liu Cai, Liu Yuwei, Feng Xuan, et al. Invert Crack Density of HTI Media by Using SVD Based on PP-Wave AVA Data from Crossing Seismic Survey Lines[J]. Journal of Jilin University: Earth Science Edition, 2013, 43(5):1655-1662.

[6] 杨培杰，穆星，印兴耀.叠前三参数同步反演方法及其应用[J].石油学报，2009, 30(2): 232-236. Yang Peijie, Mu Xing, Yin Xingyao. Prestack Three-Term Simultaneous Inversion Method and Its Application[J]. Acta Petrolei Sinica, 2009, 30(2):232-236.

[7] Fatti J L, Smith G C, Vail P J, et al. Detection of Gas in Sandstone Reservoirs Using AVO Analysis: A 3-D Seismic Case History Using the Geostack Technique[J]. Geophysics, 1994, 59(9): 362-1376.

[8] 桂金咏，印兴耀，曹丹平. 基于弹性阻抗反演理论的泊松比反演方法研究[J]. 石油物探，2011, 50(5):463-469. Gui Jinyong, Yin Xingyao, Cao Danping. Poisson’s Ratio Inversion Method Based on Elastic Impedance Inversion Theory[J]. Geophysical Prospecting for Petroleum, 2011, 50(5):463-469.

[9] 李爱山. 基于EI的岩石物性参数提取方法研究与应用[D]. 东营:中国石油大学，2008. Li Aishan. The Study on Methods of Rock Physical Properties Extraction from Elastic Impedance and Its Application[D]. Dongying: China University of Petroleum, 2008.

[10] Alemie W M. Regularization of the AVO Inverse Problem by Means of a Multivariate Cauchy Probability Distribution[D]. Edmonton: University of Alberta, 2010.

[11] Aki K,Richards P G.Quantitative Seismology[M].2nd ed. Sausalito: University Science Books, 2002.

[12] Rutherford S R, Williams R H. Amplitude-Versus-Offset Variations in Gas Sands[J]. Geophysics, 1989, 54(6):680-688.

[13] Castagna J P,Swan H W.Principles of AVO Cro-ssploting[J]. The Leading Edge, 1997, 16(4):337-342.

[14] Tarantola A. Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Philadelphia: Society for Industrial Mathematics, 2005.

[15] 张世鑫，印兴耀，张繁昌. 基于三变量柯西分布先验约束的叠前三参数反演方法[J]. 石油地球物理勘探，2011, 46(5):737-743. Zhang Shixin, Yin Xingyao, Zhang Fanchang. Prestack Three Term Inversion Method Based on Trivariate Cauchy Distribution Prior Constraint[J]. Oil Geophysical Prospecting, 2011, 46(5):737-743.

吉林大学学报(地球科学版)

荣获 “第五届中国高校精品科技期刊”称号

由教育部科技司主办、中国高校科技期刊研究会承办的“第五届中国高校精品·优秀·特色科技期刊”评比活动结果日前公布，我刊荣获“第五届中国高校精品科技期刊”称号。这是我刊首次获此殊荣，标志着我刊在提升学术影响力和竞争力，加强期刊的整体实力方面取得了一定的进展。

据了解，全国800多家高校科技期刊参与了此次评比，经专家评审，共评出中国高校精品科技期刊49种，优秀科技期刊108种，特色科技期刊30种。

本刊编辑部

2014-11-20

Non-Linear Pre-Stack Seismic AVA Inversion Based on Bayesian Theory Using Successive Iteration Method

Dai Ronghuo，Zhang Fanchang，Liu Hanqing，Li Cancan

School of Geosciences and Technology, China University of Petroleum, Qingdao 266580, Shandong,China

Conventional three-term AVA inversion methods are based on the assumption thatγ(the ratio of S-wave velocity to P-wave velocity) is a constant value usually considered to be 0.5, whileγis horizontally and vertically varied gradually in many cases. The estimated parameters of the inversion is bound to deviate from its true values withγinvariably being 0.5. and the selectionγneeds to be reasonably. Based on Bayesian theory, we presents a nonlinear pre-stack seismic AVA inversion using successive iterative method, which considered the ratio’s initial background varying horizontally and vertically and being calculated by the-given initial model, and the nonlinear inversion problem was solved by successive iteration. The proposed method gived a reasonable solution for the selection ofγand solved the nonlinear problem caused by variable ratioγ. And the accuracy and stability of the three-term AVA inversion were improved.

AVA inversion; nonlinear problem; variable ratio of S-velocity to P-velocity; successive iteration; Bayesian theory

10.13278/j.cnki.jjuese.201406302.

2014-04-10

国家自然科学基金项目(41374123)；国家“973”计划项目(2013CB228604)

代荣获(1990--)，男，研究生，主要从事地球物理反演的研究，E-mail:daironghuo@yeah.net。

10.13278/j.cnki.jjuese.201406302

P631.4

A

代荣获，张繁昌，刘汉卿，等. 基于贝叶斯理论的逐次迭代非线性AVA反演方法.吉林大学学报:地球科学版,2014,44(6):2026-2033.

Dai Ronghuo，Zhang Fanchang，Liu Hanqing, et al. Non-Linear Pre-Stack Seismic AVA Inversion Based on Bayesian Theory Using Successive Iteration Method.Journal of Jilin University:Earth Science Edition,2014,44(6):2026-2033.doi:10.13278/j.cnki.jjuese.201406302.