非自治的二人微分博弈*

张芬， 王源昌， 雷丹

(云南师范大学 数学学院，云南 昆明 650500)

1 引 言

微分博弈可以分为：自治微分博弈、非自治微分博弈、协调微分博弈、主从微分博弈等.微分博弈策略问题起源于20世纪50年代，由于军事、政治、经济等方面的需要才逐渐的将现代控制理论中的一些概念和原理引入到博弈论中.也因此微分博弈的研究越来越受到广泛的关注.

从微分博弈发展的角度来分析，不难发现运筹学中的博弈论和现代控制理论的最优控制理论对其发展有着极大的推进作用.本文主要研究的是非自治微分博弈问题.对于在一个给定区间内的线性系统以及二次性能支付函数(或非二次性能支付函数)，前人已经做了很多相关的研究[1-4].对于线性二次支付函数一般是结合黎卡提方程来给出最优策略[5-6]，而对于非二次线性支付函数一般是用拟黎卡提方程[7]来给出最优策略.在用拟黎卡提方程求解的时候一般是结合闭环表示定理来给出其最优策略的显示表达式，而本文将通过利用双方极值原理的方法给出最优策略，然后和黎卡提方程相结合.其次本文的主要思路来自于文献[8-12]，尤运程[10]研究的是自治情况下的二人微分博弈，而本文研究的是非自治情况下的二人微分博弈.关于自治和非自治的区别[2]在后面说明.

通过整理可以知道：线性二次最优控制问题是可以解到底的最优控制问题；线性非二次最优控制问题同样很重要，但是大多数情况下都只是考虑自治的情况，而本文将考虑非自治情况.给定状态方程[1-2]：

(1)

非自治和自治的主要区别在于状态方程(1)中A(·)、B(·)、C(·)是否依赖于时间变量t，如果依赖于则称其是非自治的，反之称其是自治的.其中，A(·):[t0,T)→Rn×n，B(·):[t0,T)→Rn×m，C:[t0,T)→Rn×k，y(·)∈C([t0,T];Rn)的解初始状态y0∈Rn，初始时间t0∈[0,+∞)，而u(t)和v(t)分别是取值于Rm和Rk的函数.将X=L2(t0,T;Rn)，Xc=C([t0,T];Rn),U=L2(t0,T;Rk)以及V=L2(t0,T;Rk)定义为所需要的函数空间.任何的{u,v}∈U×V称为可以执行的策略.

其性能指标函数形式如下：

(2)

其中h(·):Rn→R，且h(y(T))定义为C2(Rn)函数，R(t):[t0,T]→Rn×m,且R(t)定义为是m×m的正定矩阵，S:[t0,T]→Rn×k,且S(t)定义为是k×k的负定矩阵.

假设1.1[2]函数A(·),B(·)和C(·)满足：

且控制区域U和V都是非空的.

对于式(1)的状态方程和式(2)的性能指标函数，其中u∈U，是尽可能使性能指标函数J取极小可能值；对于v∈V，是尽可能地使性能指标函数J取极大可能值，亦即寻求最优策略(u*,v*)使：

J(u*,v)≤J(u*,v*)≤J(u,v*)

(3)

如果满足式(3)鞍点条件的(u*(t),v*(t))存在，则称(u*(t),v*(t))为二人零和微分博弈问题的最优对策，且称(u*(t),v*(t))∈U×V是J的鞍点[4]，对于所有的可行策略u∈U和v∈V.

根据最优性能指标函数的定义得：

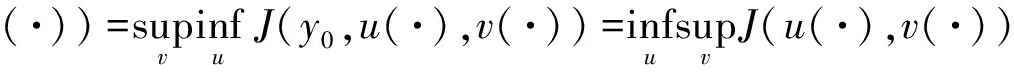
(4)

所以如果满足上式的最优策略存在[5-6]，则称J*=J(y0,u*,v*)为微分博弈的最优指标[5,7-10].

2 用双方极值原理求解最优策略

在状态方程(1)和性能指标函数(2)的基础上，考虑下面的一个微分博弈问题，即将其时间取值于区间[τ,T]上，并且τ∈[t0,T]中的任意值，用(DGP)τ来重新定义状态方程：

(5)

且其性能指标函数为：

(6)

其所要满足的鞍点条件为：

Jτ(u*(t),v(t))≤Jτ(u*(t),v*(t))≤Jτ(u(t),v*(t))

(7)

现在问题转化为寻找一对满足不等式(7)的可行策略{u*,v*}.

假设2.1[10]对于任取的τ∈[t0,T]，由(5),(6)和(7)定义的微分博弈问题存在一对鞍点策略.

从微分博弈问题的描述以及最优策略的定义不难发现，微分博弈问题和最优控制问题之间是紧密相关的，因此两者间的处理方式是类似的.所以考虑用解决最优控制问题的双方极值原理(极大极小值原理)[11]来求解线性非二次微分博弈的最优策略(u*(t),v*(t))∈U×V.

引进哈密尔顿函数H：

H(y,u,v,φ,t)=〈A(t)y(t)+B(t)u(t)+C(t)v(t),φ〉

(8)

利用双极值原理，则可以得到如下形式的共轭方程和横截面条件：

(9)

通过计算可得共轭方程的解如下：

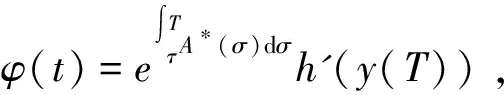
(10)

因为H分别关于u、v是二阶连续可微的，所以分别对H关于u，v求偏微分并且令其等于零，则可以知道最优控制策略{u(t)*,v(t)*}应满足下面的形式，即：

(11)

所以可以得到最优策略对{u(t)*,v(t)*}的形式如下：

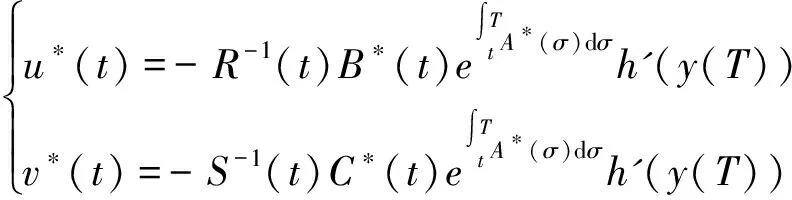
(12)

根据哈密尔顿函数的表达式可知，由上面所给出的u*(t)使哈密尔顿函数尽可能的取最小值；而v*(t)使哈密尔顿函数尽可能的取最大值，即满足下面的等式：

(13)

通过利用常数变易公式给出如下形式的状态轨迹方程：

(14)

在此将所求得的策略代入性能指标函数，通过计算得到其满足鞍点条件，最后将满足鞍点条件的策略{u*(t),v*(t)}代入上面的状态轨迹y(t)中，当t∈[τ,T]便得到下式：

(15)

令(15)中的t=T便可以得到下式：

(16)

3 拟黎卡提方程

结合(15)式给出一个非线性代数方程，其形式如下：

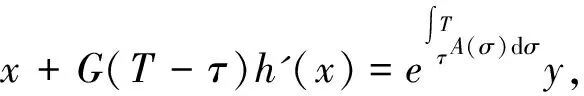
(17)

现假设对于(17)式的左边关于x求导所得到的I+G(T-τ)h''(x)是可逆的，从上式不难发现当x=y(T;y0,τ)=y(T)时就是方程(17)的一个解，对于每一个τ∈[t0,T]，定义一个映射Kτ:Rn→Rn：

Kτ(x)=x+G(T-τ)h'(y(T))

(18)

假设3.1[10]设h是Rn上的解析函数，并且K是一直强制的关于τ，只要‖x‖→∞则‖Kτ(x)‖→∞.

引理3.2[10]在假设5和(17)下，对于每一个τ∈[t0,T]，映射Kτ在Rn上是C1微分同胚映射.

引理3.3[12](隐函数的推广)若：

①映射F(t,y,x)在以点(t0,y0,x(T))为内点的区间内是一阶连续的可微映射；

②F(t0,y0,x)=0；

③映射F(t,y,x)关于t,y,x的偏导存在并且是线性同胚映射；

④映射Fx(t,y,x)≠0；

则在以点(t0,y0)为内点的领域内存在唯一的连续隐射f，使得f(T-t0,y0)=x(T)和F(t,y,f(T-t,y0))≡0，并且x=f(T-t,y)在以点(t0,y0)为内点的领域内存在连续偏导数：ft(T-t,y)，fy(T-t,y)：

ft(T-t,y)=-[Fx(t,y,f(T-t,y))]-1Ft(t,y,f(T-t,y))

(19)

fy(T-t,y)=-[Fx(t,y,f(T-t,y))]-1Fy(t,y,f(T-t,y))

(20)

证明先证隐映射f的存在性和唯一性.在点(t0,y0)附近存在点(t,y)满足下式：

F(t,y,x)=Fx(t0,y0,x(T))(x-x(T))+R(t,y,x)

(21)

其中R(t,y,x)-R(t,y,x')=ο‖x-x'‖，并且(t,y,x)和(t,y,x')都取值于(t0,y0,x(T))附近，现在去寻求在点(t0,y0,x(T))附近的F(t,y,x)=0，因此考虑下面的映射：

(22)

其中At和Ay分别是关于(t,y)在(t0,y0)附近的压缩映射[12]，且其映射到在以x(T)为中心的极小范围内.存在唯一的一个固定点x(T-t,y)关于At(x)和Ay(x)，并且关于x是连续的，所以x(T-t0,y0)=x(T)以及F(t,y,x)=0.因此x(T-t,y)是唯一的一个具有前面四条性质的连续函数，对于任何其他这样的函数必须要有一个固定点(At+Ay)x，因此只要令x(T-t,y)=f(T-t,y)便证得隐映射f是存在且唯一的.

再证(19)、(20)式，首先由于f(T-t,y)满足Lipschitz连续.由假设条件①-④知F(t,y,x)是在点(t0,y0,x(T))附近是一阶可微映射，再加上一个‖h‖足够光滑，则F(t,y,g(T-t,y))=F(t+h,y,g(T-t+h,y))=0关于(t,y,x)在点(t0,y0,x(T))附近成立.因此关于(t,y,g(T-t,y))展开F(t+h,y,g(T-t+h,y))得到：

‖Ft(t,y,f(T-t,y))+Fx(t,y,f(T-t,y))[f(T-t+h,y)-f(T-t,y)]‖

=ο(‖h‖+‖f(T-t+h,y)-f(T-t,y)‖)

(23)

由于Fx(t,y,g(T-t,y))是可逆的并且关于t连续，所以：

‖[Fx(t,y,f(T-t,y)]-1Ft(t,y,f(T-t,y))h+[f(T-t+h,y)-f(T-t,y)]‖

=ο(‖h‖+‖f(T-t+h,y)-f(T-t,y)‖)

(24)

因此存在两个独立的变量，一个常数M和另一个h，使得‖f(T-t+h,y)-f(T-t,y)‖≤M‖h‖.现在由(23)、(24)式可知f(T-t,y)是可微的，所以对F(t,y,f(T-t,y))关于t求偏导可得：

Ft(t,y,f(T-t,y))+Fx(t,y,f(T-t,y))ft(T-t,y)=0

(25)

当Fx(t,y,f(T-t,y))≠0时，由(25)得到：

ft(T-t,y)=-[Fx(t,y,f(T-t,y))]-1Ft(t,y,f(T-t,y))

同理可以用上面的方法证得：

fy(T-t,y)=-[Fx(t,y,f(T-t,y))]-1Fy(t,y,f(T-t,y))

证毕.

将方程(17)式中存在的唯一解x写成是一个关于(t,y)是一阶可微的映射H(T-·,·):[t0,T]×Rn→Rn，即

x=H(T-τ,y),τ∈[t0,T],y∈Rn

(26)

由于在(5)式中的τ是任意的，因此将(17)式中τ用t代替.定义下面的映射：

(27)

根据隐映射的条件可知F(t,y,x)是一个确定的隐映射，现在通过利用式(19)和(20)可以求出Ht、Hy，其中DKτ(x)=I+G(T-τ)h″(x)也是可逆的.

(28)

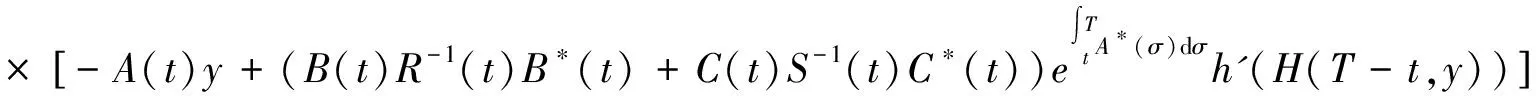
(29)

下面给出拟黎卡提方程[1]：

Pt(t,y)+Py(t,y)A(t)y+A*(t)P(t,y)-Py(t,y)(B(t)R-1(t)B*(t)

+C(t)S-1(t)C*(t))P(t,y)=0

(30)

其中(t,y)∈[0,T]×Rn.

终端条件为：

P(T,y)=h'(y) ，y∈Rn

(31)

(32)

分别对式(32)关于t、y求偏导，然后代入(30)式中，经过计算得到由式(32)所给出的P(t,y)是拟黎卡提方程的解，再由于其证明过程引自文献[10]，所以可知由双方极值原理给出的策略是唯一的最优策略，并且满足鞍点条件.

4 实例分析

例4.1 考虑下面的微分博弈问题，其状态方程为：

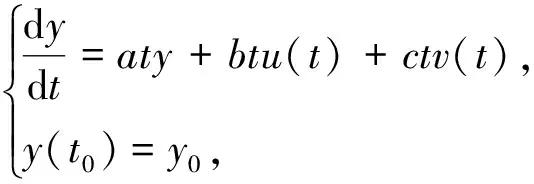
(33)

性能指标函数为：

(34)

式中：m为非零常数，r、s均为正常数，且T是固定的.

现在利用双极值原理来求解线性非二次微分博弈问题(33)、(34)式的最优策略{u*(t),v*(t)}.

首先构造哈密尔顿函数H：

(35)

由双极值原理可得到共轭方程和横截面条件为：

(36)

共轭方程的解为：

(37)

由(12)式可以得到最优策略为：

(38)

将其代入性能指标函数可知，其对应的最优性能指标满足鞍点条件，即：

J(u*(t),v(t))≤J(u*(t),v*(t))≤J(u(t),v*(t))

(39)

故由式(38)所给的策略即为最优策略.

5 结 论

根据最优控制理论给出了非自治的二人微分博弈的线性系统和性能指标.在线性非二次自治微分博弈问题的基础上，来考虑线性非二次微分博弈并时变(即非自治)的情况，然后利用双方极值原理给出非二次微分博弈问题的最优策略，最后利用拟黎卡提方程来检验所得策略是最优策略且满足鞍点条件.

在现有的非二次微分博弈基础上，下一步可以考虑用拟黎卡提方程来求解线性二次微分博弈最优策略和解决多人博弈的最优策略.或者研究更复杂的情况，结合随机因素来解决线性二次微分博弈或者线性非二次微分博弈.

参 考 文 献:

[1] 潘立平.无限维线性-非二次最优控制问题[J].数学年刊，1997,18(A):93-108.

[2] 雍炯敏，楼红卫.最优控制理论简明教程[M].北京：高等教育出版社，2006.

[3] 郭鹏，杨晓琴.博弈论与纳什均衡[J].哈尔滨师范大学：自然科学学报,2006,22(4):25-28.

[4] 朱怀念，张成科，孙佩红，等.鞍点均衡策略在动态投入产出系统中的应用研究[J].系统科学学报，2013，21(2):94-96.

[5] 姜殿玉，刘广智.二人零和连续对策上的判断与最优策略间的关系[J].运筹学学报,2004,8(2):17-23.

[6] 李树荣，张强，雷阳，等.自由时间最优控制问题的一种控制向量参数化方法[J].控制与决策,2011,26(7):1009-1013.

[7] YOU Y C.Quadratic integral games and causal synthesis[J].American Mathematical Society,1999,352(6):2737-2764.

[8] ANTIPIN A.Two-person game with nash equilibrium in optimal control problems[J].Optimal Letters,2012,6(7):1349-1378.

[9]ANTIPIN A.Extra-proximal methods for solving two-person nonzero-sum games[J].Mathematic Programming,sERIAL B,2009,120(1):147-177.

[10]YOU R C.Syntheses of differential games and pseudo-Riccati equations[J].Abstract and Applied Analysis,2002,7(2):61-83.

[11]ARONSSON G.On certain minimax problems and Pontryagin's maximum principle[J].Calculus of Variations,2010,37(1):99-109.

[12]BERGER M S.Nonlinearity and function analysis lectures on nonlinearity problems in mathematical analysis[M].New York:Academic Press,1977.