一类双线性参数化时变时滞系统的自适应迭代学习控制*

余剑平, 孙云平, 贾纳豫

(1.云南师范大学 信息学院,云南 昆明 650092；2.玉溪师范学院 信息技术工程学院，云南 玉溪 653100)

1 引 言

迭代学习控制(ILC)[1-5]自被提出以来就得到迅速发展.近年来,迭代学习控制被广泛地应用于重复跟踪问题,并且在有限时间域内,实现对目标轨迹的精确跟踪.文献[1-3]基于Lyapunov函数与复合能量函数,提出一种新的迭代学习控制方法,替代基于压缩映射的迭代学习控制.文献[4]对一类线性时滞系统提出一种迭代学习控制方法.文献[5]对非线性不确定状态时滞系统,设计基于PID类型的迭代学习控制算法,保证了系统所有信号有界性.

根据系统参数或控制增益是否被估计,迭代学习控制划分为非自适应和自适应两个方向.非自适应是在前次控制输入中增加误差信息来修正当前控制输入.自适应是利用参数或控制增益的估计值计算控制输入.自适应迭代学习控制(AILC)的研究已取得一定的成果[6-10].文献[6]基于Backstepping思想,针对二阶非线性系统的混合参数,设计出一种新型的自适应迭代学习控制算法;文献[7]通过Lyapunov技术,提出了一种全新的自适应迭代学习控制方法;文献[8]针对一类初始条件不确定的目标轨线迭代可变系统,设计出一种离散的自适应迭代学习控制算法.

时滞常常存在于各类工程系统中,造成系统控制性能的低效,甚至损坏系统稳定性，因而对时滞系统控制器和稳定性方面研究就显得尤为重要[11-14].文献[11]考虑一类时变时滞非线性参数化系统,设计一种基于参数分离与信号置换的自适应迭代学习控制算法.时滞项是未知时变[13]情况,又重新设计出新的自适应迭代学习控制策略;时滞项是周期时变[15]情况,利用重构系统方程技术与周期自适应律估计方法,设计了一种自适应学习控制方案.

关于双线性参数化系统的研究成果比较少,而对系统出现时滞问题的研究就更少了.因此,本文研究一类双线性参数化时变时滞系统,主要创新之处概括如下:

1)针对双线性参数化项,采用差分型自适应律对时变参数进行估计,微分-差分耦合型自适应律对时不变参数进行估计.

2)基于信号置换思想和参数重组技术,合并所有的时变时滞项为一个新的时变参数,有效处理了时变时滞影响.

3)设计一种基于Lyapunov-Krasovskii型复合能量函数的自适应迭代学习控制算法,该算法有效地保证了系统稳定性.

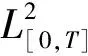
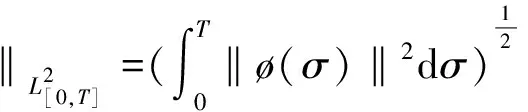
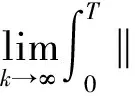
2 问题描述

考虑下述运行在区间[0,T]上的一阶双线性参数化时滞系统

(1)

式中,x、u∈R分别是系统可测状态和控制输入;θ(t)是未知连续时变参数;ω是未知时不变参数,符号已知,不妨令其大于0；b≠0是未知常控制增益,且符号已知,假定大于0.ξ(xk,t)是已知连续函数,且满足局部Lipschitz条件;f(,)是未知连续函数;τ(t)∈C[0,T]是未知时变时滞项,假定存在一个已知常数τmax，使τ(t)≤τmax,∀t∈[0,T].k∈Z+表示系统迭代次数;υ(t)是已知连续函数,表示系统初始条件.

在下文中,ξ(xk,t)记为ξk.针对系统(1)中θ(t)ξkω这一项,虽然可以采用乘法交换律,使得θ(t)与ω结合成新的时变参数,但是这种方式会降低系统的某些性能,比如时不变特性.因而,本文采用微分-差分耦合型自适应律,并用自适应迭代方式对时变和时不变参数进行估计.

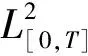
对系统(1)作出如下必要假设,以此实现本文控制目标:

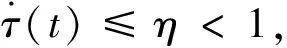
假设2 未知连续函数f(,)满足全局Lipschitz条件,即

|f(xk(t-τ(t)),t)-f(xr(t-τ(t)),t)|≤l|xk(t-τ(t))-xr(t-τ(t))|

式中,l是未知的Lipschitz常数[15-16].

假设3 对于系统(1)而言,满足xk(t)=xr(t),t∈[-τmax,0].显然ek(t)=0,t∈[-τmax,0],∀k∈Z+.

3 构造控制律与参数自适应律

系统(1)在第k次迭代时,其跟踪误差的动态方程表示如下:

=θ(t)ξkω+buk+φ(t)+Λk

(2)

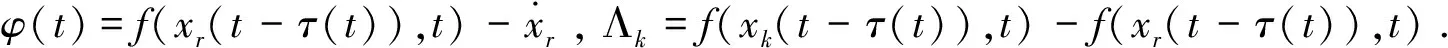
根据假设2易知,Λk满足下述不等式

|Λk|≤l|xk(t-τ(t))-xr(t-τ(t))|≤l|ek(t-τ(t))|

(3)

针对时滞系统(1),设计出了一个Lyapunov泛函,用于处理系统(1)中带有时滞的一项

(4)

对(4)式中的Lyapunov泛函求导,可得

(5)

将(2)式代入(5)式,可得

(6)

根据(3)式,下列不等式恒成立

(7)

(8)

将(8)式代入(6)式,易得

(9)

根据假设1进一步简化(9)式,可得

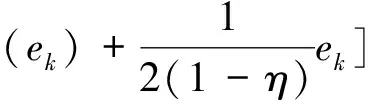
(10)

根据(10)式,设计学习控制律为

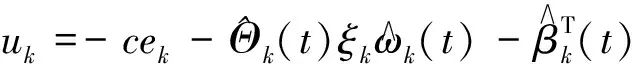
(11)

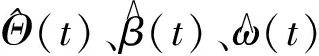
设计时变参数Θ(t)的自适应律为

(12)

设计时变参数β(t)的自适应律为

(13)

设计时不变参数ω的自适应律为

(14)

式中,q1>0、q2>0、q3>0均为可设计的参数常增益.

将(11)式代入到(10)式中,可得

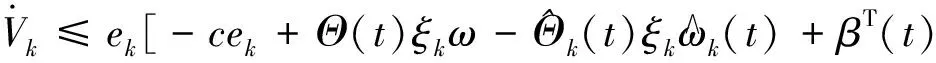
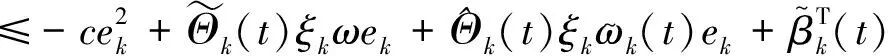
(15)

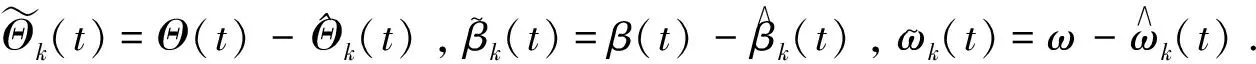
4 收敛性分析

定理系统(1)在假设1-3、学习控制律(11)以及参数自适应律(12)-(14)下,具备如下特性:

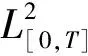
证明第k次迭代时,定义一个Lyapunov-Krasovskii型复合能量函数

(16)

a)计算Ek(t)在第k次与第k-1次迭代时差分

ΔEk(t)=Ek(t)-Ek-1(t)

(17)

根据(4)式与(15)式,以及假设3,计算(17)式右边第一项,可得

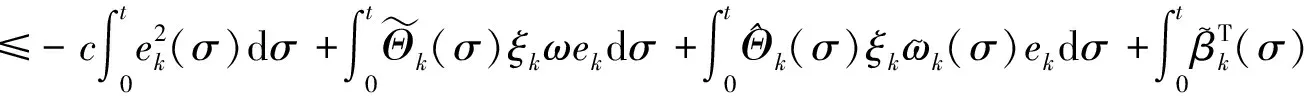
(18)

利用代数关系式(a-b)2-(a-c)2=(c-b)(2(a-b)+(b-c))以及参数自适应律(12)式,计算(17)式右边第三项,可得

(19)

利用恒等式(a-b)T(a-b)-(a-c)T(a-c)=(c-b)T(2(a-b)+(b-c))以及参数自适应律(13)式,计算(17)式右边第四项,可得

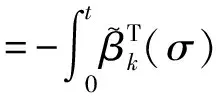
(20)

(21)

将(18)-(21)式代入(17)式,可得

(22)

令t=T,并且利用(4)与(14)式,可得

(23)

b)证明跟踪误差收敛性

根据(23)式,并且反复利用(17)式,可得

(24)

通过(4)式与(16)式可知,E0(t)是关于t的连续函数,根据连续有界性定义可知,E0(t)在区间[0,T]上有界,因此E0(T)是有界的.进而根据(24)式,可知Ek(T)也是有界的.

对(24)式两边求极限,可得

(25)

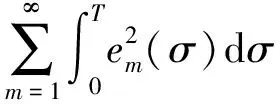
c)证明系统中所有信号有界性

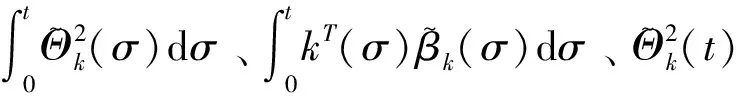
5 仿真实例

考虑以下运行在区间[0,2π]上的一阶双线性参数化时滞系统

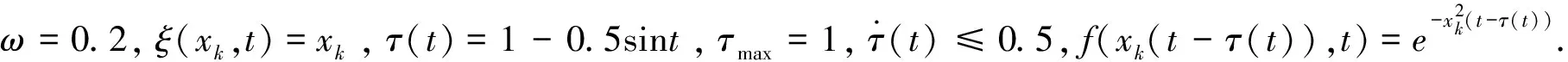
期望轨迹xr(t)=sint,系统中不确定项满足下列不等式

设计控制增益,选取c=0.5,η=0.5,q1=0.5,q2=0.4,q3=0.6,b=0.3.

仿真结果如图1-5.图1表明了跟踪误差的收敛性,图2-5分别给出控制律曲线与参数估计曲线,表明了系统所有信号的有界性.

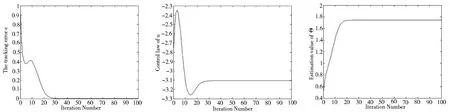
图1 跟踪误差e曲线 图2 控制律u曲线 图3 时变参数Θ(t)估计曲线

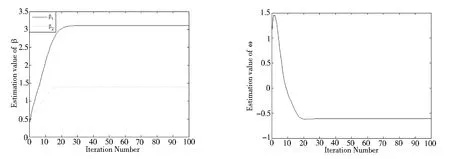
图4 时变参数β(t)估计曲线 图5 时不变参数ω估计曲线

6 结 论

提出了一种基于Lyapunov-Krasovskii型复合能量函数的自适应迭代学习控制方法,并且应用于双线性参数化时变时滞系统中,该方法结合微分-差分耦合型自适应律,信号置换思想,参数重组技术及不等式技巧,使得跟踪误差在固定时间域内渐近收敛到0.最后,利用仿真实例验证了该方法的有效性和可行性.

参 考 文 献:

[1] QU Z H,XU J X.Model based learning control and their comparisons using Lyapunov direct method[J].Asian Journal of Control(Special issue on ILC),2002,4(1):99-110.

[2] XU J X.The frontiers of iterative learning control-part II[J].Journal of Systems Control and Information,2002,45(5):233-243.

[3] XU J X,TAN Y.A composite energy function-based learning control approach for nonlinear systems with time-varying parametric uncertainties[J].IEEE Transactions on Automatic Control,2002,47(4):1940-1945.

[4] PARK K H,BIEN Z,HWANG D H.Design of an iterative learning controller for a class of linear dynamic syste-ms with time delay[J].IEE Proceedings-Control Theory and Applications,1998,145(8):507-512.

[5] CHEN Y,GONG Z,WEN C.Analysis of high-order iterative learning control algorithm for uncertain nonlinear systems with state delays[J].Automatica J.IFAC,1998,34(9):345-353.

[6] 孙云平,李俊民,王元亮.二阶系统非一致目标跟踪混合自适应迭代学习控制[J].工程数学学报,2008,25(1):10-16.

[7] FRENCH M,ROGERS E.Non-linear iterative learning by an adaptive Lyapunov technique[J].International Journal of Control,2000,73(10):840-845.

[8] CHI R H,HOU Z S,XU J X.Adaptive ILC for a class of discrete-time systems with iteration-varying trajectory and random initial condition[J].Automatica,2008,44(8):2207-2213.

[9] CHIEN C J.A combined adaptive law for fuzzy iterative learning control of nonlinear systems with varying control tasks[J].IEEE Transactions on Fuzzy Systems,2008,16(1):40-51.

[10]TAYEBI A,CHIEN C J.A unified adaptive iterative learning control framework for uncertain nonlinear systems[J].IEEE Transactions on Automatic Control,2007,52(10):1907-1913.

[11]李俊民.非线性参数化时变时滞系统自适应迭代学习控制[J].数学物理学报，2011,31A(3):682-690.

[12]李俊民,王元亮,李新民.未知时变时滞非线性参数化系统自适应迭代学习控制[J].控制理论与应用，2011,28(6):861-867.

[13]陈为胜,王元亮,李俊民.周期时变时滞非线性参数化系统自适应学习控制[J].自动化学报，2008,34(12):1556-1560.

[14]郑平安,孙云平,杨昆,等.含有时变延迟的双线性参数化系统的重复学习控制[J].云南师范大学学报：自然科学版，2014,34(1):1-8.

[15]王丽，徐明跃.拟单边Lipschitz非线性系统的自适应观测器设计[J].哈尔滨师范大学学报：自然科学版，2013，29(5)：10-12.

[16]迟于孟，王秋琳，周磊.一类Lipschitz非线性系统观测器设计[J].哈尔滨师范大学学报：自然科学版，2014，30(4)：1-4.