基于小波分析的遥测设备角误差信号降噪研究

庞岳峰， 李 娟， 褚福勇

(酒泉卫星发射中心指挥控制站 酒泉 732750)

基于小波分析的遥测设备角误差信号降噪研究

庞岳峰， 李 娟， 褚福勇

(酒泉卫星发射中心指挥控制站 酒泉 732750)

介绍角跟踪及小波降噪的原理，描述不同的小波基、分解层数以及阈值的选取对遥测角误差信号降噪效果的影响，并给出判断降噪效果的定量标准。采用六种常用小波基在不同阈值和分解层数下对含噪声角误差信号进行降噪处理，并采用MATLAB进行仿真，通过对降噪效果的比较分析得出最佳方案。最后，针对一代小波运算复杂的问题，在设备实现时采用提升小波，并用实测数据对降噪效果进行检验。

角误差； 小波； 仿真； 降噪

引 言

对空中目标的自动跟踪一般通过在方位和俯仰两个平面上进行角跟踪实现，因而需要获得方位和俯仰的角误差信号，为此需要四个馈源振子接收信号，形成四个对称的相互重叠的波束，信号处理后解出角误差的大小和方向。在该工作方式下，伺服系统接收来自接收机的误差信号，经过数字处理、放大后驱动天线朝减小误差的方向移动，完成对目标的自动跟踪。

由于信号在接收过程中会受到设备接收信道噪声、空间背景噪声及各种干扰等随机因素的影响，解调出的角误差信号中不可避免地含有噪声，而含噪角误差信号会影响动态目标自跟踪的准确性并引起天线振荡。对角误差信号进行降噪处理，可以提高设备自跟踪的稳定性和准确度。

小波分解可以把各种频率组成的混合信号按照不同的分辨尺度分解成一系列不同频率的块信号，由此可对特殊频率范围内的噪声进行滤波处理，其灵活滤波的特性是其它方法无法比拟的[1]。目前小波分析在信号降噪、图像增强等方面已经得到广泛研究[2～4]，利用MATLAB软件的小波工具包对信号小波处理效果进行仿真变得非常普遍[5，6]，然而小波分析在航天测控系统应用方面的研究较少。本文将小波分析方法引入航天测控系统遥测设备角误差信号的处理中，通过降低角误差信号中的噪声改善设备的跟踪性能。

1 小波降噪基本原理

1.1 离散小波变换

在实际应用中，尤其是在计算机上实现，连续小波必须加以离散化。这里的离散化都是针对连续的尺度函数a和连续的平移参数b的，而不是针对时间变量t的，与以前习惯的时间离散化不同，需要注意区别[7]。

设ψ(t)是一个基本小波函数，对它进行伸缩和平移变换，如式(1)所示。

为方便起见，在离散化中，总是限制a取正值，这样相容性条件就变为

通常，把连续小波分析中的尺度参数a和平移参数b的离散化公式分别取作a＝aj0、b＝kaj0b0，这里k，j∈Z，扩展步长a0是非1的固定值，为方便起见，总是假定a0＞1，选择一个合适的b0＞0，使得ψ(t-kb0)能覆盖整个时间轴而且信息不会丢失。于是，对应的离散小波函数ψj，k(t)就写作

而离散化小波分析系数则可以表示为

其重构公式为

其中，C是一个与信号无关的常数[1]。

这里，a0和b0的选择是保证重构信号精度的重要因素，为了使小波分析具有可变化的时间和频率分辨率，从而适应待分析信号的非平稳性，需要改变a0和b0的大小，使小波分析具有“变焦距”的功能。在实际应用中采用动态采样网格，而最常用的是二进制的动态采样网格：a0＝2，b0＝1，每个网格点对应的尺度为2j，平移为2jk。由此得到的小波函数

称为二进小波。一般来说，一维信号的降噪处理过程分为以下三个步骤进行[6，8]：

①选择一个小波函数并确定小波分解的层次N，然后对信号S进行N层小波分解；

②从第一层到第N层的每一层高频系数中选择一个阈值进行量化处理；

③根据小波分解的第N层的低频系数和经过量化处理后的第一层到第N层的高频系数，进行一维信号的小波重构。

1.2 多分辨率分析

多分辨率分析从空间的概念上形象地说明了小波的多分辨率特性，它将之前的所有正交小波基的构造法统一起来，给出了正交小波的构造方法以及正交小波分析的快速算法，即Mallat算法[8]。关于多分辨率分析的原理，我们以一个三层的小波分解进行说明，小波分解和重构原理如图1所示。

图1 三层分辨率Mallat小波分解和重构示意图

从图1中可以看出，多分辨率分解只是对低频部分进行一步分解，而高频部分不予考虑。分解的关系为S＝A3+D3+D2+D1。

2 角误差信号小波降噪仿真与分析

2.1 仿真环境及仿真结果判定标准

噪声是不可预测的随机信号，主要在信号的获取和传输中产生。为了模拟含噪角误差信号，首先记录了一段遥测设备跟踪固定信标的角误差数据，在理想状态下，该方位和俯仰的角误差都趋于零。然后采用-0.05～0.05的随机数模拟高斯白噪声进行叠加，加入随机数后角误差信号如图2所示。

选择的软件仿真环境是Windows xp+Matlab 7.7.0.471+Wavelet Toolbox 4.3，构建的模拟角误差信号样本点数为2500。在不同小波函数、分解层数及不同阈值估计方法选择下进行仿真，并对仿真采取软阈值下“Scaled white noise”模型。

为了对仿真效果进行定量比较，我们引入信噪比(SNR)与均方根误差(RMSE)作为判断标准，其定义如下

图2 模拟含噪声的角误差信号

其中，fi为降噪后数据，gi为原始数据，从定义看出信噪比越大，均方根误差则越小，平滑效果越好。

2.2 小波函数对降噪效果的影响

小波分析中应用到的小波函数ψ(x)具有多样性，而不同的小波基分析同一个问题会产生不同的结果，所以在工程应用中小波分析的一个十分重要的问题是最优小波基的选择。在面对某一具体应用时，除了要选择比较各小波基本身的正交性、对称性、正则性、紧支集、消失矩等性能，还要注意具体应用环境的制约。目前主要是通过对仿真结果的比较来判定小波基的好坏，并由此选定最优小波基。

对模拟含噪角误差信号用Db6小波、Sym2小波、Dmey小波、Haar小波、Bior3.3小波以及Rbio6.8小波进行三层分解降噪，采用MATLAB对降噪效果进行仿真，图3～图8为六种小波三层分解固定阈值降噪后效果。

降噪前、后信号的信噪比与均方根误差计算结果见表1。

图3 Sym2小波三层分解固定阈值降噪效果

图4 Haar小波三层分解固定阈值降噪效果

图5 Dmey小波三层分解固定阈值降噪效果

图6 Bior3.3小波三层分解固定阈值降噪效果

图7 Db6小波三层分解固定阈值降噪效果

图8 Rbio6.8小波三层分解固定阈值降噪效果

表1 采用不同小波降噪仿真效果

从表1的角误差信号降噪效果可以看出，Db6小波、Sym2小波和Rbio6.8小波降噪后信号信噪比(SNR)相对较大，均方根误差(RMSE)相对较小，即这三种小波对角误差信号的降噪效果较好，而其中Db6小波降噪效果最好。

2.3 分解层数对降噪效果的影响

分解层数的选取也对信号降噪效果有很大的影响。原始信号不变，分别采用Db6小波、Sym2小波和Rbio6.8小波对原始信号进行降噪处理，从理论上讲，可选取的最大分解层数为，N为信号长度，代表向下取整运算[7]。采用不同分解层数的Db6小波、Sym2小波和Rbio6.8小波进行降噪仿真，降噪效果见表2。

表2 采用不同分解层数三种小波的降噪仿真效果对比

在工程实践中，最大分解尺度J的值没必要取太大，一般取J＝3～5即可。事实上J越大，噪声和信号表现的不同特征越明显，越有利于信噪分离；但另一方面，对重构来讲，分解层数越多，失真越大，即重构误差越大，而且分解层数的增加会导致计算量的增大。表2仿真结果表明，对含噪角误差信号作降噪处理，Db6小波选J＝4最优，Sym2小波选J＝3最优，Rbio6.8小波选J＝4最优。

2.4 阈值选择对降噪效果的影响

可以把阈值理解成刻画信号的小波系数与噪声的小波系数之间的一条分界线，只有选择合适的分界线，才能将原信号与噪声最大限度地区分开来，以达到降噪的目的。如果选择过大的阈值，会去除原信号本身信息，重构后数据失真严重；如果选择过小的阈值，则平滑效果不明显。

固定阈值定义：设含噪声信号f(k)在尺度1～j(1＜j＜J)上通过小波分解得到的小波系数的个数总和为n，附加噪声的标准偏差为σ，则阈值Rigorous SURE是一种基于无偏似然估计原理的自适应阈值选择，Heuristic SURE是最优预测变量阈值[8]，Minimax是一种固定的阈值选择形式，产生的是一个最小均方差的极值，而不是无误差[7]。

对Db6小波四层分解、Sym2小波三层分解和Rbio6.8小波四层分解分别采用不同阈值估计方法进行仿真，降噪效果见表3。

表3 三种小波采用不同阈值估计方法的降噪效果对比

从仿真结果可以看出，不同阈值估计方法对降噪效果的影响明显小于不同小波和不同分解层数对降噪效果的影响。对于不同的小波，最优的阈值是不同的，对文中的数据样本降噪时，Db6小波四层分解阈值采用Heuristic SURE最优，Rbio6.8小波四层分解和Sym2小波三层分解阈值采用固定阈值最优。

3 遥测设备角误差降噪的实现

遥测设备通常采用单通道单脉冲跟踪体制，信道中传输的信号既包含遥测信息也包含跟踪角误差信息，角误差信息是通过调幅形式传输的，跟踪接收机将调制在载波上的幅度信息通过相干解调电路进行同步检波、数字滤波以及斜率修正等一系列工作后得到天线方位、俯仰与飞行目标偏角成正比的误差电压，送天线控制单元完成跟踪。

为了更方便检验所选取小波对角误差信号的降噪效果，结合目前遥测设备特点提出了通过控制和差信号幅度进行角误差信号模拟的方案，实现对角跟踪误差信号的动态模拟。对遥测跟踪接收机和天线控制单元来说，其处理真实目标角误差信号与模拟角跟踪误差信号的过程完全一致，通过模拟角误差检验降噪效果的方法是可行的。

3.1 角误差信号的动态模拟

角误差信号模拟的实现思路如下：

①在基带组合上装订任务理论弹道和设备布站站址，设置触发起飞零点后读取弹道并算出当前天线理想状态的方位、俯仰角进行插值处理，获取天线实时角并作插值处理后与理想状态的方位、俯仰角求差。

②充分利用遥测设备基带组合调制板的上行调制功能，找出向特定内存地址写入的数值与所产生调幅信号的对应关系，通过向内存定时写入数值产生模拟调频和调幅信号。

③基带组合调制板产生1kHz基准信号，供基带接收解调模块解角误差信号使用。

④模拟信号在设备内部闭环，经过上变频、下变频送至基带接收解调单元进行遥测解调和角误差解调，解出角误差信号送天线控制单元驱动天线跟踪。

设备硬件已经具备所需功能，通过在基带组合上开发软件完成角误差信号模拟功能，角误差信号模拟原理如图9所示。

设备天线控制单元发送角度数据的周期是20Hz，程序读取本地理论弹道的速度是1点/秒，对读取的理论弹道进行Lagrange三点二次插值。插值具体计算公式为

插值后形成每秒20点的弹道，再与天线角度数据作差。然后向内存写入与角度差对应的值，实现天线闭环控制，使天线平稳地向理论跟踪方位和俯仰角运行。经测试，内存写入值与所产生的误差电压对应关系如图10。

图9 角误差信号模拟原理

图10 内存写入值与所产生的误差电压对应关系

3.2 小波降噪算法的实现

仿真中所采用的小波是第一代小波，在用Mallat快速算法实现时依赖于傅立叶变换，需要用伸缩、平移一个母函数构成小波基，运算相对复杂。1998年，Daubechies和Sweldens证明任意具有有限冲击响应滤波器的离散小波变换都可以通过一系列简单的多步提升步骤来解决[9]。这一结论建立起了第一代小波变换和第二代小波变换之间的联系，即所有能够用Mallat快速算法实现的离散小波变换都可以用第二代小波方法来实现。第二代小波是一种更为快速有效的小波变换实现方法，它的优势是算法简单，运算速度快，占用内存少，执行效率高，可以分析任意长度的信号。提升算法是构造第二代小波的一种方法，它与用传统小波变换的Mallat算法处理后的信噪比相近，但提升小波算法计算量有所减少，去噪更为快速[10]。

遥测设备的天线控制单元是角误差信号的最终使用终端，其天线控制软件采用C++实现。为便于和设备现有软件统一，在天线控制单元采用C++进行提升小波变换，实现角误差降噪处理。提升算法过程分为分裂、预测和更新三个步骤，文献[10]中详细阐述了提升小波的具体算法，文献[11]论述了提升方案的小波变换原理以及C++实现，用一系列C++类实现了提升方案的小波变换并支持用户自定义的小波。研究表明，在同样的数据长度条件下，采用第二代小波变换方法可将变换速度至少提高1倍以上[9]。因此，可将其用于角误差信号的实时降噪处理。

3.3 角误差降噪效果

对三套遥测设备分别进行了六次实验。前三次被检设备对角误差电压采用传统的处理方式，后三次被检设备在天线控制单元对采集的角误差电压进行了降噪处理，对三套遥测设备的测试数据进行分析比对，三套设备在采用角误差降噪后方位和俯仰的跟踪均方差如表4所示。

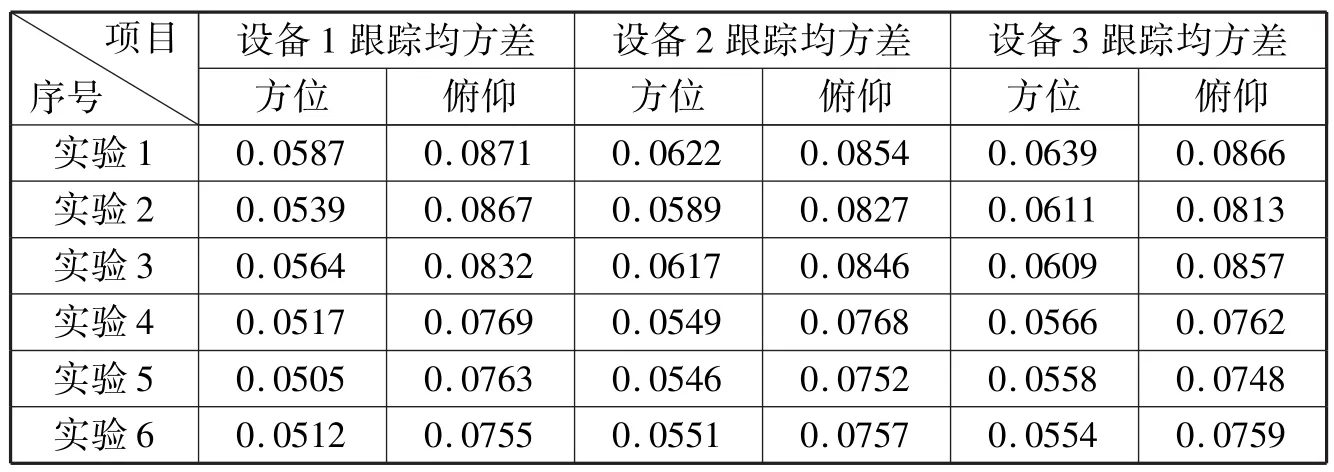
表4 三套设备降噪效果测试情况

经计算，三套设备采取降噪算法后的跟踪方位和俯仰均方差比原均方差分别降低了9.3%、10.6%、10.1%、9.8%、9.3%和10.7%。由于三套设备降噪处理后效果基本相同，本文只取设备1角误差降噪前、后理论跟踪方位/俯仰角与实际跟踪方位/俯仰角差值进行比较，如图11～图14。

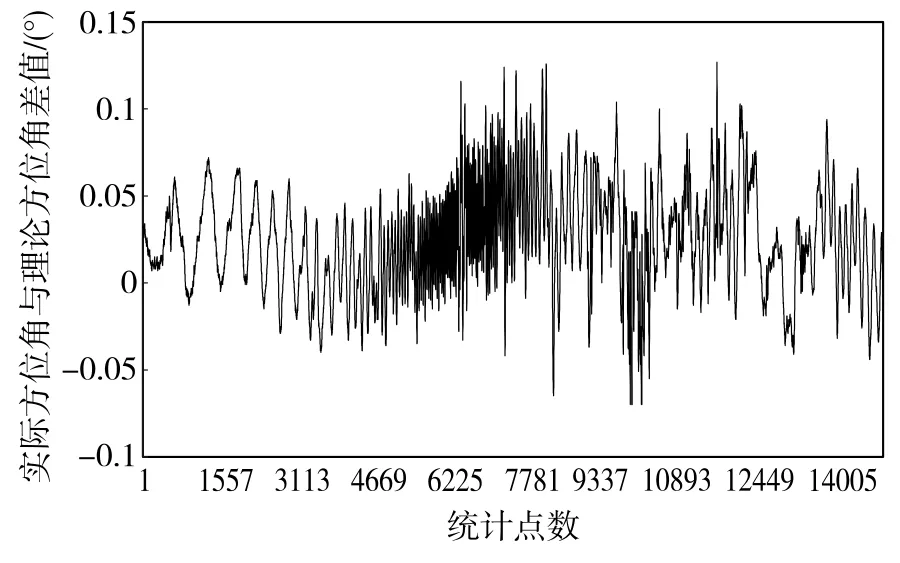
图11 降噪前设备1理论与实际方位角差值

图12 降噪后设备1理论与实际方位角差值

图13 降噪前设备1理论与实际俯仰角差值

图14 降噪后设备1理论与实际俯仰角差值

4 结束语

在处理不同信号时，小波基、阈值和分解层数的选取没有固定不变的数学模型，一般通过大量的试验或经验公式获得。在利用小波函数对角误差信号的降噪平滑中，小波基的选取对角误差信号降噪效果影响最为明显，分解层数的影响次之，阈值选择的影响较小。六种常用小波基中，Db6小波4层分解并采用Heuristic SURE阈值对含噪角误差信号的处理效果最好。

[1]Daubechies Ingrid.小波十讲[M].李建平，杨万年，译.北京：国防工业出版社，2003.

[2]李 媛.小波变换及其工程应用[M].北京：北京邮电大学出版杜，2010.4.

[3]陆 伟.基于提升小波理论的信号降噪方法的研究[D].沈阳：东北大学硕士论文，2009，28.

[4]蒋 鹏.小波理论在信号降噪和数据压缩中的应用研究[D].杭州：浙江大学博士论文，2004：63～64.

[5]赵海英，纪超辉.小波变换降噪技术及其在Matlab中的实现[J].兵工自动化，2006，25(2)：54～55.

[6]周 伟.MATLAB小波分析高级技术[M].西安：西安电子科技大学出版社，2006.

[7]Donoho D L，Johnstone I.Wavelet Shrinkage Asymptopia[J].Jounal of Royal Statistical society series(B)，1995，9 (4)：365～368.

[8]梁学章，等.小波分析[M].北京：国防工业出版社，2005.

[9]Daubechies L，SweldensW.FactoringWavelet Transforms into Lifting Steps[J].Fourier Anal Appl，1998，4(3)：247～269.

[10]张永学，陈丽霞，钟正斌.提升小波变换在信号去噪中的应用[J].石油仪器，2007，21(1)：80～82.

[11]郭景峰，苑炜弢，姜爱群.基于提升方案的小波变换原理与C++实现[J].计算机工程与科学，2004，26(1)：102～105.

Research on Angle Error Signal Denoising in Telemetry Equipment Based on W avelet Analysis

Pang Yuefeng， Li Juan， Chu Fuyong

The principles of angle tracking and wavelet denoising are introduced.The impacts of wavelet basis function，decomposition level and threshold selection on telemetry angle error signal denoising are analyzed.And the standard for denoising effect evaluation is given.Six wavelet basis functions are used to denoise the angle error signal with noise under different decomposition levels and thresholds.Simulations are carried outwith MATLAB to find out the best solution through the comparison of denoising effects.Finally，aiming at the complexity of generation wavelet algorithm，the lifting wavelet is put into practice.And themeasurement data verify the effect of wavelet denoising.

Angle error signal； Wavelet； Simulation； Denoise

TP391.9

A

CN11-1780(2014)06-0038-07

2014-04-21 收修改稿日期：2014-07-21

庞岳峰 1980年生，学士，2002年毕业于重庆大学数学系，工程师，从事信号处理研究工作。

李 娟 1984年生，硕士，2013年毕业于北京航空航天大学，工程师，从事通信工程、无线电技术研究。

褚福勇 1986年生，硕士，2010年毕业于国防科技大学计算机学院，工程师，从事遥测地面站工作。