船载雷达补偿跟踪技术研究及应用

姚熠飞， 李志坚， 常 硕， 郭书明

(中国卫星海上测控部 江阴 214431)

船载雷达补偿跟踪技术研究及应用

姚熠飞， 李志坚， 常 硕， 郭书明

(中国卫星海上测控部 江阴 214431)

一般大型雷达天线的伺服系统，由于机械结构的谐振频率不高，伺服系统带宽受到限制，跟踪动态目标时滞后误差较大。对于二阶无静差系统来说，主要是加速度滞后误差较大。为了解决这个问题，防止丢失目标，提出一种复合控制技术，在系统中采用前馈补偿的方法，可以显著减小跟踪动态滞后。

船载雷达； 补偿； 复合控制

引 言

船载雷达伺服系统是测角系统的重要组成部分，它接收来自接收机的误差信号，经数字处理、放大后送给伺服电机，驱动天线向减少误差的方向运动，从而完成对目标的跟踪。目标角加速度和角加加速度都会导致目标跟踪的动态滞后。为了减小动态滞后误差，要求跟踪环具有高的开环放大倍数和快的动态响应能力[1]。

负反馈系统一般都是靠位置校正网络对误差信号进行变换来改善系统的稳定性和暂态性能[2]。如果要求显著提高系统的精度，同时又具有一定的暂态指标，则采用单一的校正方法很难实现。为解决这个问题，文本提出一种复合控制方法，又称前馈补偿。

1 传统方法

天线控制的根本目的就是实现对目标的快速捕获及精确跟踪，并使之达到系统要求的跟踪性能和跟踪精度。系统采取经典控制理论设计，即环路结构。各个环的信号处理仍将是基于偏差控制，并采用频率域的方法进行设计校正[3]。在控制结构上采用典型的位置环、速度环、电流环三环结构，其中位置环是保证跟踪性能的外环[4]。

传统的单回路系统基本结构如图1所示[5]。

我们可利用系统开环传递函数KW(s)计算系统的动态性能指标。

图1 单回路系统

雷达自动跟踪目标时，目标运动会造成电轴指向与目标真实方向间的差异，具体说就是目标相对于雷达运动的角位移、角速度、角加速度会造成测量误差，称为动态滞后误差。天线自跟踪环路采用二阶无静差系统，动态滞后主要是由目标相对于雷达运动的角速度的变化，即相对角加速度引起的[6]。目标相对于雷达运动的角加速度越大，动态滞后误差越大。实际标校中，可以使雷达自跟踪航路捷点附近目标，此时，目标离雷达距离最近，目标相对于雷达运动的角加速度最大，信噪比最高，接收机热噪声等其它误差较小，误差电压主要是由动态滞后引起的，因而近似地可以用此段路径上的误差电压和角误差灵敏度来表征相应点的动态滞后误差，即

式中，ΔU为误差电压，μ为角误差灵敏度，Δθ为动态滞后空间误差角[7]。

2 前馈补偿方案

基于前馈补偿的复合控制系统基本结构如图2所示。

与传统的单回路系统相比，复合控制系统除了一般的闭环系统之外，还包含一个开环控制部分KcWc(s)。

系统的闭环传递函数为

图2 复合控制系统结构

由式(3)可以看出，只要KcWc(s)中没有不稳定环节，则增加一个开环控制部分，对系统的稳定性没有影响。

要减小误差，就是要使输出与输入相一致。

令θ0(s)＝θi(s)，解得

此时，没有误差，即实现所谓的完全不变性。

对于实际伺服系统，K2W2(s)中含有一个积分环节，即

式中，Tc为滤波时间常数。

因此要实现完全的不变性，不仅困难，而且往往会产生相反的效果，这是因为此时虽然由于目标引起的动态滞后误差减到最小，但KcWc(s)的引入使该支路噪声等干扰直接进入高带伺服内环，而增大了随机误差，导致未必一定能够得到好的总体效果。

为了减小动态滞后误差，同时又不致过多地增大随机误差，复合控制系统提取目标的速度信号，在目标较近时加入KcWc(s)通道，可在低频段近似实现不变性，能显著改善雷达系统的动态跟踪性能。

对于滤波时间常数Tc，若取值过大，则所提取的目标速度信号损失大，前馈效果差，但相应地由此而引入的随机误差较小；若Tc过小，则所提取的目标速度信号损失小，前馈效果好，但相应地由此而引入的随机误差较大，因此Tc需根据系统实际情况进行选择[8]。

3 设计与验证

3.1 总体方案

陀螺稳定环、自跟踪环设计为典型的二阶系统，其校正运算在计算机内完成，同时采用智能算法对大小信号的模型变化及调节器的积分项进行补偿。

伺服系统主要由天线控制单元、天线驱动系统等部分组成，其控制对象为天线座。天线控制单元由计算机系统、A/D、D/A、信号调理、控保系统、显示器等组成。它的主要任务是实现位置闭环，对天线进行位置控制[9]。

复合控制原理如图3所示。复合控制也称为补偿，补偿输入点在陀螺环的指令输入处，补偿功能是通过计算机软件实现的。

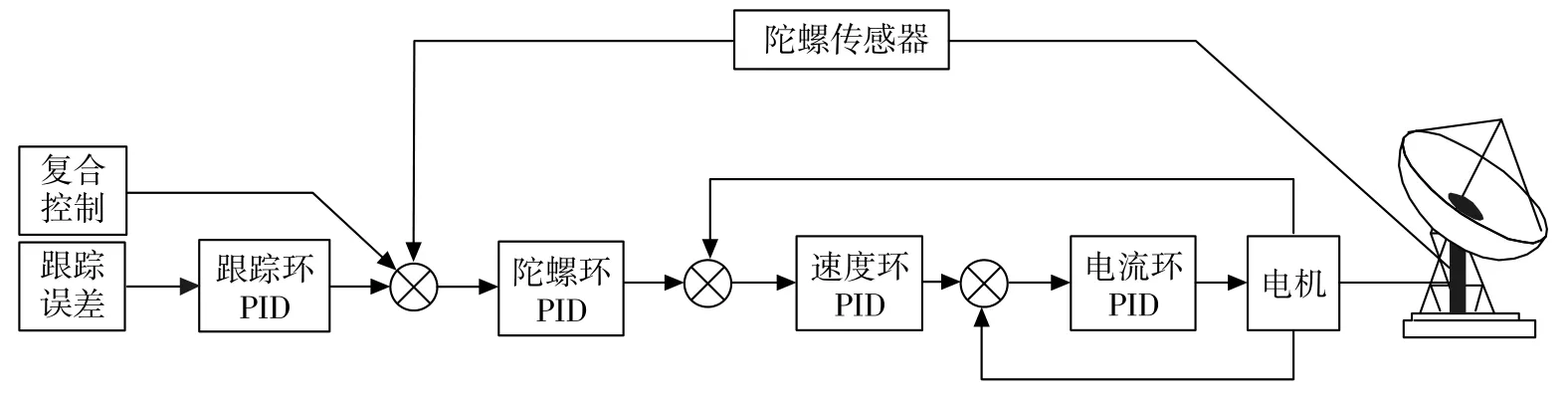
图3 复合控制原理

3.2 软件设计

天线控制单元软件在Win2000环境下，使用DELPHI语言编程。当选择复合控制功能时，将目标前馈变量加入陀螺环前端，前馈效果通过环路作用于电机，驱动天线，达到减小动态滞后误差的目的。程序关键语句如图4所示。

图4 复合控制功能实现程序

在进行设备调试时，需先进行加速度误差常数测试，其软件流程为：由天线控制单元软件自动产生一个匀加速运动指令S＝(1/2)at2，经插值列表后作用于天线伺服系统，程序控制天线运动。计算机自动记录带时标的天线角位置数据，将当时的数据θ实际与理论计算数据θ理论作比较，由计算机自动计算出加速度误差常数。

3.3 试验验证

以某船载雷达系统为例，分别对方位和俯仰无/加补偿状态下的加速度误差常数进行测试，结果如表1所示。加速度误差常数体现了雷达系统跟踪动态快速目标的能力，其数值越大，跟踪性能越佳。

从表1中数据可以看出，加前馈补偿后加速度误差常数得到显著改善，雷达系统稳定跟踪性能更佳，与理论模型分析结果一致。

表1 加速度误差常数测试结果

利用雷达系统跟踪国际空间站等快速运动目标，在不加补偿和加补偿两种状态下分别进行动态滞后误差测试，结果如表2所示。

表2 动态滞后误差测试结果

在两种状态下分别进行测角随机误差统计，结果如表3所示。从表3中数据可以看出，无补偿和加前馈补偿后的测角随机误差基本一致，并未增大。

表3 测角随机误差测试结果

根据上述数据分析，加前馈补偿后，在未增大随机误差的情况下，方位和俯仰动态滞后误差角度明显减小，总体跟踪效果良好。

4 结束语

加速度误差常数的大小直接取决于结构谐振频率的大小，环路调节器的设计只是在有限的范围内作调整，以保证系统满足必要的相位裕度。使用复合控制技术可以大幅提高加速度误差常数，当雷达系统跟踪快速运动目标时，动态滞后误差将显著减小。本文通过试验分析，验证了补偿跟踪技术的实用性和可靠性。

[1]李连升.现代雷达伺服系统[M].北京：国防工业出版社，2003.

[2]江文达.航天测量船[M].北京：国防工业出版社，2002.

[3]胡金辉，黄 坤，李志坚，陈小刚.船载大型测控系统自适应跟踪技术研究[J].科学技术与工程，2012，12(32)：8539～8542.

[4]丁求启.船载雷达天线复合控制技术研究[J].科学技术与工程，2013，13(15).

[5]姚景顺，杨世兴.舰载雷达的动态标校[J].火力与指挥控制，2008，(03)：128～134.

[6]唐瑞春，马华民，赵友刚，翟翌立.带有持续扰动非线性系统的最优跟踪控制[J].系统仿真学报，2006，18(10)：2882～2885.

[7]钟德安，张同双，李晓勇，冯鸿奎.基于标校经纬仪的测量船坞内标校新方法[J].无线电工程，2009，(07)：49～52.

[8]瞿元兴.航天测量船测控通信设备船摇稳定技术[M].北京：国防工业出版社.

[9]韩恩典，李 培，蔡 睿，常 硕.高仰角弧段雷达跟踪不稳定因素分析[J].科学技术与工程，2011，11(24)：5826～5830.

Investigation and App lication of Com pensatory Tracking Technique for Shipborne Radar

Yao Yifei， Li Zhijian， Chang Shuo， Guo Shuming

The bandwidth of servo system for shipborne radar is confined，because of the low resonant frequency.The main factor is the error of acceleration lag for the second-order steady-state zero-error system.The paper puts forward a new technique of complex control to solve this problem and prevent the loss of target.Themethod of feed-forward compensation is adopted，and the dynamic lag decreases obviously.

Shipborne radar； Compensation； Complex control

V556.6

A

CN11-1780(2014)06-0067-04

姚熠飞 1989年生，大学本科，助理工程师，研究方向为船载雷达伺服控制系统。

李志坚 1983年生，大学本科，工程师，研究方向为船载雷达伺服控制系统。

常 硕 1986年生，大学本科，助理工程师，研究方向为船载雷达伺服控制系统。

郭书明 1978年生，大学本科，工程师，研究方向为船载雷达伺服控制系统。

2013-12-17 收修改稿日期：2014-04-15