对 CAPM模型在A股市场有效性的检验

闵梓耕

（东北财经大学 研究生院， 辽宁 大连 116025）

对 CAPM模型在A股市场有效性的检验

闵梓耕

（东北财经大学 研究生院， 辽宁 大连 116025）

本文通过对选取的行业中性的上证A股市场的150只股票的实证分析，检验了CAPM模型在上证A股市场中的有效性.本文的研究方法参考Fama-French（1992）中的方法，将验证过程分为三步，通过将样本分为不同的组合再进行回归，估计其β值，最后一步建立检验模型对CAPM是否在中国股票市场上成立作出检验.检验的结果为在中国当前的A股市场中，CAPM模型很难解释股票的收益，即CAPM模型并不能很好的适用于当前的A股市场.

CAPM模型；上证A股；实证检验

资本资产定价模型(CAPM)可以说是现代金融理论的基石之一.一方面,在市场达到均衡时,资产的合理价格是什么,这是所有市场参与者共同关注的一个焦点,因而也自然成为金融以及经济理论研究的核心.另一方面,它又与市场有效性问题的研究密不可分.正如Fama(1991)所指出的,我们不可能单独检验市场有效性,任何对市场有效性的检验总是与某种资产定价模型结合在一起的,即存在所谓“联合检验”问题.CAPM有两层基本的含义:第一,证券的期望收益率是关于β因子的线性函数;第二,不同证券在期望收益率上的差异仅仅是由于它们的β因子不同,也就是说,与公司特征有关的个别因素不影响证券的期望收益率.自从Sharp、Lintner以及Black提出CAPM以来,国外学者就该模型在西方成熟资本市场尤其是美国资本市场上的适用性问题做了大量实证研究,既有支持该模型的实证结果,也有否定该模型的证据,比如众多反常现象的存在.

1 CAPM模型

CAPM有多种形式.Sharpe-Lintner模型假定投资者能够以无风险资产利率进行借贷,其数学表达式为:

其中 E[Ri]为第 i项资产的期望收益率,E[Rm]为有效市场组合的期望收益率,βi=cov(Ri,Rm)/var(Rm).

Black放松了投资者可以按无风险利率借贷的假设,推导出了零 -βCAPM:

对 CAPM的实检验一般针对 Sharpe-Lintner模型进行,本文也是如此.

CAPM从理论上说明在有效资产组合中,β 描述了一项资产的系统风险,由于非系统风险可以通过同时持有多项资产而消除掉,资产的期望收益仅与该资产的系统风险相关,非系统风险得不到定价.因此,对 CAPM的检验实际上就是验证β是否对资产的期望收益具有完全的解释能力.

CAPM模型的理论假设：

（1）证券市场是有效的,即信息完全对称无风险证券存在，投资者可以自由地按无风险利率借入或贷出资本投资总风险可以用方差或标准差表示，系统风险可用系数表示；

（2）所有的投资者都是理性的，他们均依据马科威茨证券组合模型进行均值方差分；

（3）作出投资决策证券加以不征税，也没有交易成本，证券市场是无摩擦的；

（4）每种证券的收益率分布均服从正态分布，交易成本可以忽略不计，每项资产都是无限可分的，这意味着在投资组合中，投资者可持有某种证券的任何一部分.

（5）数据处理可采用 OLS最小二乘法.

检验方法：

如果 CAPM有效,且真实市场组合可以得到,则对任意资产均有(1)式成立,即有E[Ri]=Rf+βim(E[Rm]-Rf)成 立.由于Rf,E[Rm]-Rf对于各项资产是一样的,这就可以通过各项资产的横截面回归对CAPM进行检验.先进行时间序列回归,计算出β:

之后可以用下列模型进行检验：

其中:Rit代表个股 i在 t时刻的周超额收益率；Rpt表示组合在 t时期的超额收益；βpt代表由（3）式回归所得的各股票或投资组合的 β 值；γ0，γ1为待估计的参数.

2 文献综述

美国经济学家哈里·马科维茨（Markowits）于 1952年创立的资产组合理论最认为最佳投资组合应当是具有风险厌恶特征的投资者的无差异曲线和资产的有效边界线的交点.从 20世纪 60年代初开始，以夏普(w．Sharpe，1964)，林特纳(J．Lintner，1965)和莫辛(J．Mossin，1966)为代表的一些经济学家开始从实证的角度出发，探索证券投资的现实.他们分别提出了单指数模型，并提出以对角线模式来简化方差－协方差矩阵中的非对角线元素.夏普据此建立了资本资产定价模型(CAPM)，指出无风险资产收益率与有效率风险资产组合收益率之间的连线代表了各种风险偏好的投资者组合.

CAPM模型表达简洁，推理严密，但是 CAPM模型仍然是基于各种假设之上的理论模型，这个模型在现实中是否有效一直饱受经济学家的争论.在众多对 CAPM模型的验证中，EF Fama,KR French在 1992年发表的 《The cross‐section of expected stock returns》以清晰的思路，严密的论证建立了对 CAPM的验证模型，此后很多经济学家使用这样的模型或类似的方法针对不同情况下，不同国家不同时间段的股票市场的表现对 CAPM模型进行了验证.

Fama和 Macbeth在其 1992年的实证检验中发现股票平均收益和 β 之间的线性关系在 1963—1990年间消失,即使把β单独作为解释变量也是如此.他们在解释变量中加入了公司规模,账面价值/市场价值,市盈率和两个杠杆变量,账面资产 /市场价值,账面资产 /账面价值.经过回归分析,F ama和 Macbeth发现,公司规模和账面价值 /市场价值包含了股票平均收益中杠杆和市盈率的作用,对平均收益的截面变动有明显的解释能力;β 不论是单独作为解释变量换还是和其它变量一起回归,均不能拒绝其系数显著为零的假设.由此 Fama和 Macbeth得出结论说,CAPM不能说明近50年的平均股票收益.

阮涛、林少宫对上海证券市场40支单个股票进行了CAPM检验,在仅包含β作为解释变量的横截面回归中,β的系数显著为零,R2仅为0.004555;将非系风险加进回归方程,β的系数变为负值仍显著为零,非系统风险系数为正,且在5%的显著性水平上不为零,从而否定了CAPM在上海证券市场的有效性.但由于单支股票检验的误差较大,其结论并不可靠.陈小悦、孙爱军运用Fama和Macbeth(1973)的方法对我国股市作了检验,在控制了股本规模以后,β对收益没有解释能力;在β、股本规模和方差的组合作为解释变量的回归中,均不能拒绝β的系数为零的假设,从而否定了CAPM在我国股票市场有效性.

3 检验方法与过程

我们使用从2011年1月1日到2013年12月31日上证A股市场不同行业的150只股票的复权周收益率作为样本.

检验过程：

首先将样本按照时间跨度分为三组，即 2011年这 150只股票的涨跌幅数据，2012年的数据，2013年的数据分别作为三个步骤中使用的样本.

首先运用第一期的数据，模型如下：

其中 Rit和 Rmt分别是单个股票的超额收益率和市场组合的超额收益率.

通过此次对β的估计，我们可以发现在所有样本中β值的差异较大，从 0.5到 1.5不等，没有明显小于 0的 β 值.

之后按照β的大小将股票分为十五组，每组十只，这样是因为单只股票的非系统风险较大，同时，单只股票的收益数据容易受到停牌等其他因素的影响.因此此后两步的检验将以这十五个组合为研究样本.

第二步将要运用一年 52周的收益数据估计每个组合的β值：

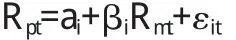
其中 Rpt为组合 p的超额周收益，Rmt为市场组合的超额周收益.

回归结果如下：

组合 组合1 组合2 组合3 组合4 组合5 组合6 β 值 0.54802 0.600292 0.624615 1.001221 0.784233 1.080867组合 组合 7 组合 8 组合 9 组合 10 组合 11 组合 12 β 值 1.176609 1.083724 1.166418 1.069631 1.121748 1.01368组合 组合 13 组合 14 组合 15 β 值 1.25999 1.22434 1.244611

模型 R2值均大于 0.6.最小为 0.62.通过对系数的检验，每次回归系数均显著不为0.说明模型可以较好地体现组合超额收益与市场超额收益间的关系.

第三步将要使用如下的检验模型：

其中 Rpt为组合的超额收益率，εpt为随机扰动项.

我们这里的回归与分析方法是对 Fama-MacBeth (1973)所采用方法的简化.因为我们所取的样本时期比较短,只有第二年的数据用来计算组合的β系数,只有第三年的收益率数据用来与二年的β系数相匹配，其中 是第二步回归的残差的标准差，以此表示组合的非系统风险.

这一步检验主要检验股票市场的现实收益是否能使用CAPM模型解释：

1.资产的期望收益与其系统风险是线性的即有 γ0=0，γ2=0；

2.在一个投资者回避风险的市场，资产的期望收益与其

系统风险正相关，即 γ1>0，且 γ1=E[Rm]-Rf.

回归的结果如下：

系数 γ0 γ1 γ2 模型 R2 模型 F 值 模型 P 值估计值 -0.06652 0.055453 -0.00485 0.004289 0.025844 0.974541 t 值 -0.07344 0.025994 -0.00412 p 值 0.942665 0.97969 0.996782

通过回归结果可以看出回归模型的 R2只有 0.004，说明模型不能很好地解释超额收益与系统风险之间的关系.参数 γ1不显著大于 0，其他三个参数都不是显著非 0.这说明β值和组合的超额收益很可能是非相关的，我们不能得出系统性风险和超额收益之间的线性关系的结论.

同时，通过对组合超额收益的 t检验 （H1=t-test(R3, B2(2),0.05);结果为 H1=1，拒绝原假设），也证明在 5%的显著水平上，t-test的输出结果为拒绝 γ1=E[Rm]-Rf的假设.

以上的检验结果说明：

1.回归结果不能说明存在正的无风险收益.

2.回归结果不能说明市场上系统风险与收益存在正相关，表明系统风险不足以解释股票组合的预期收益,这与C A P M理论假设不相符合,其他风险因素在股票定价中起着重要作用.

4 研究结论

本文的研究结果表明，CAPM模型理论依然不是完全适合沪市目前的发展状况，市场上存在着在较大程度上影响股票收益的其他因素，这些因素无法用系统风险解释，所以当前还无法通过 CAPM对中国 A股市场的股票进行比较准确的定价.

最后，这次检验结果虽然可以在一定程度上说明我国的A股股票市场存在不能被系统风险解释的其他因素，这些因素属于非系统风险并对股票收益率有难以忽视的影响.但是，本次检验的模型本身还有很多值得改进的地方，一个简单的方法是将模型变为：

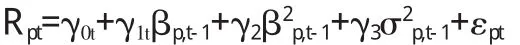
其中，新添入项 σp,t-1为第二期的回归中的残差的标准差，这项可以用来解释一定的非系统风险对 Rpt的影响.如果进一步进行改进，可以参考 Fama-French(1992)中的方法，将此项用 ME（股票的总市值），PB（股票的市净率）代替，变为三因素的模型，这个模型可以更好地解释超额收益与系统风险的关系.

〔1〕Eugene F.Fama,James D.Macbeth,1973, “R isk,Return, Equilibrium:Empirical Tests”,Journal of Political Economy,607-636.

〔2〕Eugene F.Fama,Kenneth French,1992, “The Cross-Section of Expected Stock Returns”,Journal of Finance, 427-465.

〔3〕Richard Roll,Stephen Ross,1994,“On the Cross-Sectional Relation between Expected Returns and Betas”,Journal of Finance,101-121.

〔4〕John Y.Campbell,Andrew W.Lo,A,Craig Mackinlay,1997,“The Econom itrics of Financial Markets”,Princeton University Press.

〔5〕Alan L.Tucker,Kent G.Becker,M ichael J.Isimbabi,Joseph P.Ogden,1994,“Contemporary Portfolio Thoery and R isk Management”,W est Publishing Company.

〔6〕陈浪南,屈文洲.资本资产定价模型的实证研究[J].经济研究,2000(4).

〔7〕陈小悦,孙爱军.CAPM 在中国股市的检验[J].北京大学 学报,2000(4).

〔8〕阮涛,林少宫.CAPM 模型对上海股票市场的检验[J].数理统计与管理,2000(7).

〔9〕Roll,R.,1977,“A Critique of the Asset Pricing Theory′s Tests(Part 1):On Past and Potential Testability of the Theory”,Journal of Financial Econom ics,4,pp.129-176.

〔10〕Shanken,Jay,1985,“Multivariate Tests of the Zero-Beta CAPM”,Journal of Financial Economics,14,327-348.

〔11〕Stambaugh,Robert F.,1982,“On the Exclusion of Assets for Tests of the Two-parameter Model:ASensitivity Analysis”,Journal of Financial Econom ics,10,237-268.

〔12〕Zhou,G.,1991, “Small Sample Tests of Portfolio Efficiency”,Journal of Financial Economics 30,pp.165-191.

〔13〕杨朝军,邢靖.上海股票市场 CAPM 实证检验.上海交通大学学报,1998，32（3）.

〔14〕陈小悦,孙爱军.CAPM 在中国股市的有效性检验.北京大学学报，2000（4）.

F830.91

A

1673-260X（2014）09-0034-03