基于niche的直接T-S模糊自适应控制

郝云力，王茂华

（1.阜阳师范学院 信息工程学院；2.阜阳师范学院 数学与金融学院，安徽 阜阳 236041）

基于niche的直接T-S模糊自适应控制

郝云力1，王茂华2

（1.阜阳师范学院 信息工程学院；2.阜阳师范学院 数学与金融学院，安徽 阜阳 236041）

此提出了一种新型的基于 N iche的直接模糊自适应控制，把含有参数的生态位贴近度作为零阶的 T-S 型后件，采用超稳定理论设计模糊控制器并得到了后件参数的自适应律，体现了生物界个体的自组织、自学习、自适应的能力.该方法简化了控制器设计，不需要监督控制项．同时降低了对最小逼近误差的要求，从而使方案更容易实现．通过对肌型血管疾病的仿真验证了本方法的可行性.

直接自适应；T-S 模糊系统；生态位；贴近度；超稳定理论

1 引言

自从 1985年日本的 Takagi和 Sugeno提出了一种新的模糊模型（T-S）以来，T-S模型成为一些专家学者研究的热点，因为它便于设计以保证系统的稳定性和比 Mamdani型具有更好的逼近性能.文等提出了直接鲁棒自适应控制的方法，在等效控制器的基础上加了监督控制器，但是，它还要求知道估计误差的界，而这在实际中不一定能获得.而利用超稳定理论改进了原有的直接型模糊控制器，给出了新的设计方案，简单化了模糊控制器的规则和结构，放宽了对误差平方可积的条件，提高了直接型模糊控制器的运行效率.

冗余性和稳定性是生态系统具有的特点，生物界的生物个体在具体环境中具有进化适应的功能，与系统环境平衡相处.生态位在此起着重要作用，利用这种特点，将生态系统的生态位与模糊控制相结合，得到了模糊控制器后件参数的自适应律，体现了生物界中生物个体的自适应、自组织、自学习的能力，使模糊控制的背景有了实际的生物意义.最后通过对肌型血管系统模型[4]的实例分析仿真说明此方法的有效性.

2 直接自适应模糊控制器的设计

考虑如下形式的n阶非线性系统：

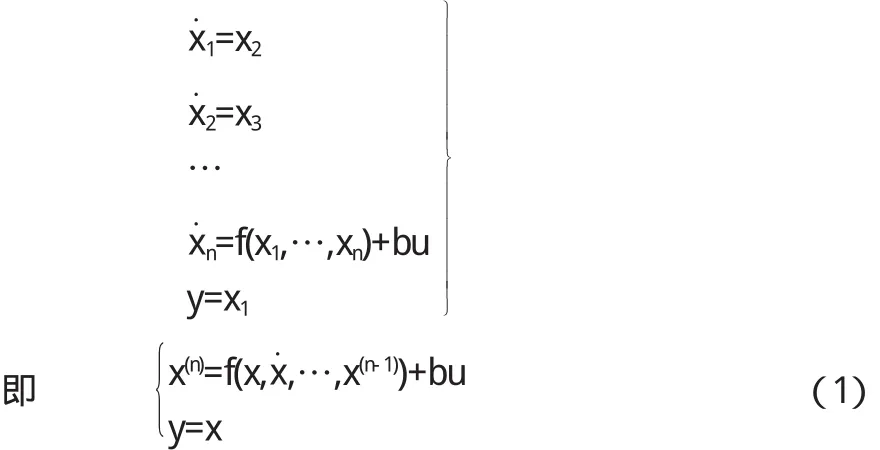
u∈R和∈R分别是输入和输出，x=(x1,…,xn)T=(x,x˙,…,x(n-1))∈R假设是通过量测可以得到的状态向量.如果非线性函数f(x,x˙,…,x(n-1))和 b是已经知 道的，就 选择控制器 u来除去 其非线性性质，选择形式如下的控制器[3]：

Rl：如果 x1是且…且则

这里(x1,x2,…,xn)可看成是生态位的实际生态因子，模糊控制后件代表实际生态位状态与理想生态位状态的大小差异有多少？这种差异是由贴近度函数表示.

有上面贴近度函数可以看出，此后件是一个零阶的 T-S模型.为方便起见，我们用来代替

在达到假设(1)的情况下，采用[5]的方法，则得到基于生态位的模糊子系统表达为如下的形式：

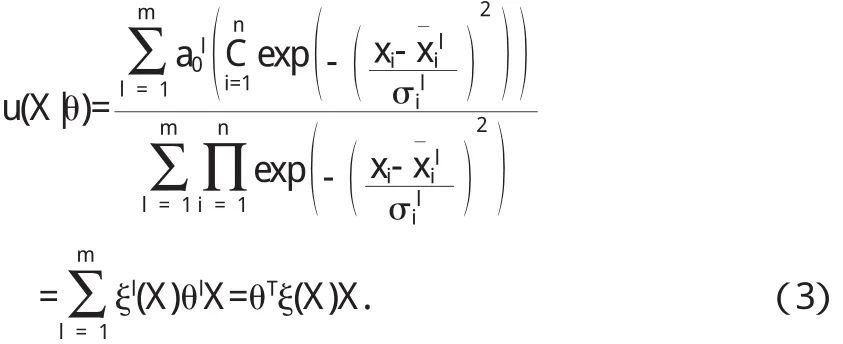
这里

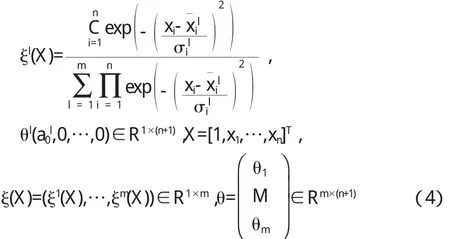
将（3）以及（4）式代入（4-1）式中，整理可得

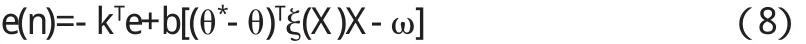
采用文献[7]的方法得到自适应律为

对（9）式关于 t求导，并整理得

(θ)T=αvξ(X)Xdt+θ0，结合 v=De=eTPB，有[7]知，再令 α=Γ可得出

则

进而有贴近度式求得

3 实例仿真

本例对肌型血管疾病进行控制仿真[4].肌型血管的数学模型为：

其中 x是肌型血管内径的变化差,y是肌型血管里面的压力差,τ是和时间成正比的“时间变量”，Ecosωτ血管受到的周期性刺激的干扰，m,n,h为常参数.

在系统（13）第二个式子加上一个控制器 u，则得到：

为了建立输出y与控制器u的直接关系，需要对y求导，令 y=x˙，经过求导后得：

y˙ =(h+mh)(mx+ny)-(h+mh)[-(h+mh)x-(h+nh)y+hx3

则(19)式可以写为：y˙=f(X)+g(X)u

取 m=-0.15，n=-1.7，h=-0.65，E=0.3，ω=1，选择控制器参数

k1=2,k2=1,α=10,β=20,θ0=0，若取 Q=diag(2,2)，则有（9）可求得 d0=1,d1=1.选,取理想的 λ=0,σ=1，则有自适应律：

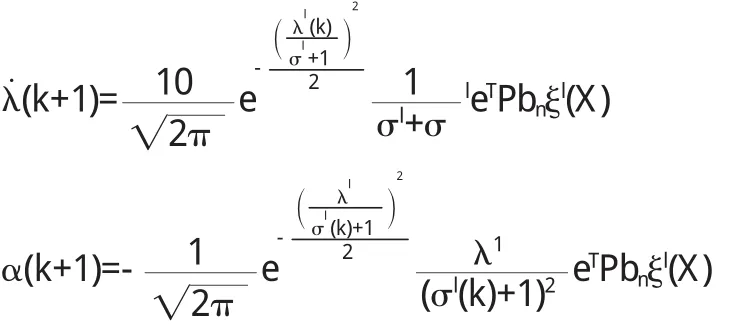
初始状态设为 x(0)=10,y(0)=10，令目标参考信号 ym=1.0,则仿真图为：

图 1 受控系统（18）的系统响应：状态量 x是实线，状态量y是虚线

4 结论

本文将生态位的贴近度作为零阶的 T-S型模糊后件，采用超稳定理论改进了原有的直接型模糊控制器，给出了新的控制方案，简单了控制器的规则和结构，放宽了对误差平方可积的条件，减少模糊推理的规则数，并且不需要考虑监督控制器，使自适应模糊控制器的结构简单化了同时也提高了其运行效率．得到了模糊控制器后件生态位贴近度参数的自适应律，在生物界中体现了生物个体的自适应、自组织、自学习的能力.也使模糊控制的背景有了实际的生物意义.肌型血管系统的仿真验证了本方法的可行性.

〔1〕T.Takagi,M.Sugeno.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Trans. Systems Man Cybernet,1985(15):116–132.

〔2〕S.G.Cao,N.W.Rees,G.Feng.Analysis and design for a class of complex control systems[J].Part II:fuzzy controller design,Automatica,1997(33):1029-1039.

〔3〕张明君，张化 光.一种鲁 棒 直接自适 应 模糊控制 算 法[J].东北大学学报,2006（27）：5-8..

〔4〕张天平.直接鲁棒自适应模糊控制[J].系统工程与电子技术，2002（8）：76-78.

〔5〕王舰.基于超稳定的改进直接自适应模糊控制器[J].哈尔滨理工大学学报,2004（4）：85-88.

TP391.9

A

1673-260X（2014）09-0018-02

国家自然科学基金项目（11226140）；阜阳师范学院自然科学基金项目（2013FSKJ09）资助