Group Twisted Tensor Biproducts over Hopf Group Coalgebras

CHEN Quan-guo,TANG Jian-gang

(School of Mathematics and Statistics,Yili Normal University,Yining 835000,China)

Group Twisted Tensor Biproducts over Hopf Group Coalgebras

CHEN Quan-guo,TANG Jian-gang

(School of Mathematics and Statistics,Yili Normal University,Yining 835000,China)

In this paper,we introduce the concept of a group twisted tensor biproduct and give the necessary and sufficient conditions for the new object to be a Hopf group coalgebra.

Hopf group coalgebra;twisted tensor biproduct;comodule coalgebra

§1.Introduction

As a generalization of ordinary Hopf algebras,Hopf group-algebras appeared in the work of Turaev[1]on homotopy quantum f i eld theories.A purely algebraic study of Hopf groupcoalgebras can be found in the references[29].

As a generalization of Majid’s double cross products,a general product AT⊗RB between two bialgebras A and B connected via a twisted map R:B⊗A→A⊗B and a cotwisted map T:A⊗B→B⊗A was introduced in Caenepeel et al[10].The product construction AT⊗RB is equipped with both smash product constructionand smash coproduct construction A×TB on A⊗B.In particular,the authors derived in Caenepeel et al[10,Theorem4.5]necessary and sufficient conditions for ATRB to be a bialgebra.Recently,by weakening the condition that A is a bialgebra replaced by that A is both an algebra and a coalgebra(but not necessarily bialgebra),Ma Tian shui and Wang Shuan hong[11]introduced a twisted tensor biproduct denoted by ATRB,generalizing Radford’s bismash products in Radford[12].

The aim of this paper is to give a general version of the twisted tensor biproducts(called group twisted tensor biproduct).We give the necessary and sufficient conditions for the new object to be a Hopf group coalgebra.

The article is organized as follows.

In Section 2,we recall the def i nitions and some of the basic properties of Hopf group coalgebras,group(co)module(co)algebras,respectively.

In Section 3,we introduce the group twisted tensor biproduct ARTB={ARTBα}α∈π, where π is a discrete group and B is a semi-Hopf π-coalgebra,A is only an algebra and a coalgebra connected by a twisted map R={Rα:Bα⊗A→A⊗Bα}α∈πand a cotwisted map T={Tα:A⊗Bα→Bα⊗A}.We f i nd the necessary and sufficient conditions for the new object ARTB to be a Hopf π-coalgebra(see Theorem 3.1).

§2.Preliminaries

Throughout,k is a f i xed f i eld and π is a discrete group with unit e.Unless otherwise stated, all vector spaces are over k and all maps are k-linear.

2.1π-Coalgebras

A π-coalgebra is a family of k-spaces B={Bα}α∈πtogether with a family of k-linear maps Δ={Δα,β:Bαβ→Bα⊗Bβ}α,β∈π(called a comultiplication)and a k-linear map ε:Be→k (called a counit)such that Δ is coassociative in the sense that

for any α,β,γ∈π and

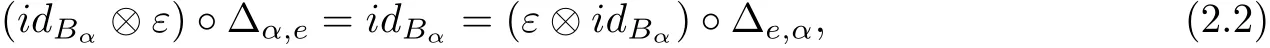
for all α∈π.

Following the Sweedler’s notation for π-coalgebras,for any α,β∈π and b∈Bαβ,one write

2.2Hopf π-Coalgebras

A semi-Hopf π-coalgebra is a π-coalgebra B=({Bα}α∈π,Δ={Δα,β},ε)such that the following datas hold.

Each Bαis an algebra with multiplication mαand unit 1α∈Bα,for all α,β∈π,Δα,βand ε:Be→k are algebra maps.

A semi-Hopf π-coalgebra B=({Bα,mα,1α}α∈π,Δ={Δα,β},ε)is called a Hopf π-coalgebra, if there exists a family of k-linear maps S={Sα:Bα→Bα−1}α∈π(called an antipode)such that

2.3π-B-Comodule Coalgebras

Let B=({Bα}α∈π,Δ={Δα,β},ε)be a π-coalgebra and(V,ΔV,εV)a coalgebra.V is called a left π-comodule coalgebra,if there exists a family of maps ρV={:V→Bα⊗V}α∈π, which will be called a comodulelike structure and denoted by(v)=v(−1,α)⊗v(0,α),satisfying the following conditions

(i)For any α,β∈π and v∈V,we have

(ii)For any α∈π and v∈V,

(ii)V is counitary in the sense that,for any α∈π and v∈V,

2.4π-B-Module Algebras

Let B=({Bα,mα,1α}α∈π,Δ={Δα,β},ε)be a semi-Hopf π-coalgebra and A an algebra with the unit 1A.A is called a left π-B-module algebra,if the following conditions hold

(1)A is a left Bα-module,for each α∈π;

(2)b·(aa′)=(b(1,α)·a)(b(2,β)·a′),for all b∈Bαβand a,a′∈A;

(3)b·1A=ε(b)1A,for all b∈Be.

§3.Group Twisted Tensor Biproducts

In this section,we shall introduce the concept of a group twisted tensor biproducts and give the necessary and sufficient conditions for the new object to be a Hopf π-coalgebra.

3.1Group Twisted Tensor Products

Let A be an algebra with unit 1Aand B={Bα,mα,1α}α∈πa family of algebras.Suppose that R={Rα:Bα⊗A→A⊗Bα}α∈πis a family of linear maps.The A#RB is def i ned to be a family of vector spaces{A⊗Bα}α∈πwith the product given by

where aRα⊗bRα=arα⊗brα=Rα(b⊗a),for all b,b′∈Bαand a,a′∈A.We say that A#RB is a π-twisted tensor product,if each A#RBαis an associative algebra with the unit 1A#1α.In the case,the map R is called a twisted map.

Proposition 3.1With the notation as above.Then A#RB is a π-twisted tensor product if and only if the following conditions hold

for all a,a′∈A,b,b′∈Bα.

ProofStraightforward.

3.2Group Twisted Tensor Coproducts

Let(A,ΔA,εA)be a coalgebra and B=({Bα}α∈π,Δ={Δα,β},ε)a π-coalgebra.Given a family of linear maps T={Tα:A⊗Bα→Bα⊗A}.Then the π-twisted tensor coproduct A×TB={A⊗Bα}α∈πhas the coproduct given by

where bTα⊗aTα=btα⊗atα=Tα(a⊗b),for all b∈Bαand a∈A.We say that A×TB is a π-twisted tensor coproduct,if A×TB is a π-coalgebra with the counit εA⊗ε.The map T is called a cotwisted map.

Proposition 3.2With the notation as above.Then A×TB is a π-twisted tensor coproduct if and only if the following conditions hold,for all α,β∈π

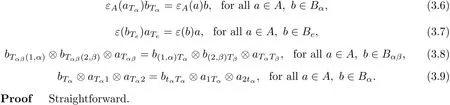
3.3Group Twisted Tensor Biproducts

Theorem 3.1Let B=({Bα,mα,1α}α∈π,Δ={Δα,β},ε,S={Sα})be a Hopf πcoalgebra.Let A be both an algebra and a coalgebra(but not necessarily bialgebra)so that there exists a linear map SA:A→A satisfying SA(a1)a2=1AεA(a)and a1SA(a2)=1AεA(a). Then the following statements are equivalent

1)The conditions(C1)∼(C8)such that,for all a,a′∈A

(C7)aRαβ1⊗bRαβ(1,α)Tα⊗aRαβ2Tα⊗bRαβ(2,β)=a1Rα⊗b(1,α)TαRα1αtα⊗1ATαa2tαrβ⊗b(2,β)rβ,for all a∈A,b∈Bαβ;

(C8)εRe=ε⊗εAand εAis an algebra map. 2)(ATRB={ATRBα}α∈πε¯,S¯)is a Hopf π-coalgebra,where the multiplication,ε¯eandS¯ are given as

In this case,we call ATRB a π-twisted tensor biproduct.

Proof1)⇒2)By(C1),we have that ATRB is a family of associative algebras.By (C2),we know that¯Δ=¯Δα,βis coassociative and¯ε is the counit.

In what follows,we prove thatis an algebra homomorphism.Indeed,let T=t=U= u=s and R=r=P=p,we compute,for all a,a′∈A,b,b′∈Bαβ,

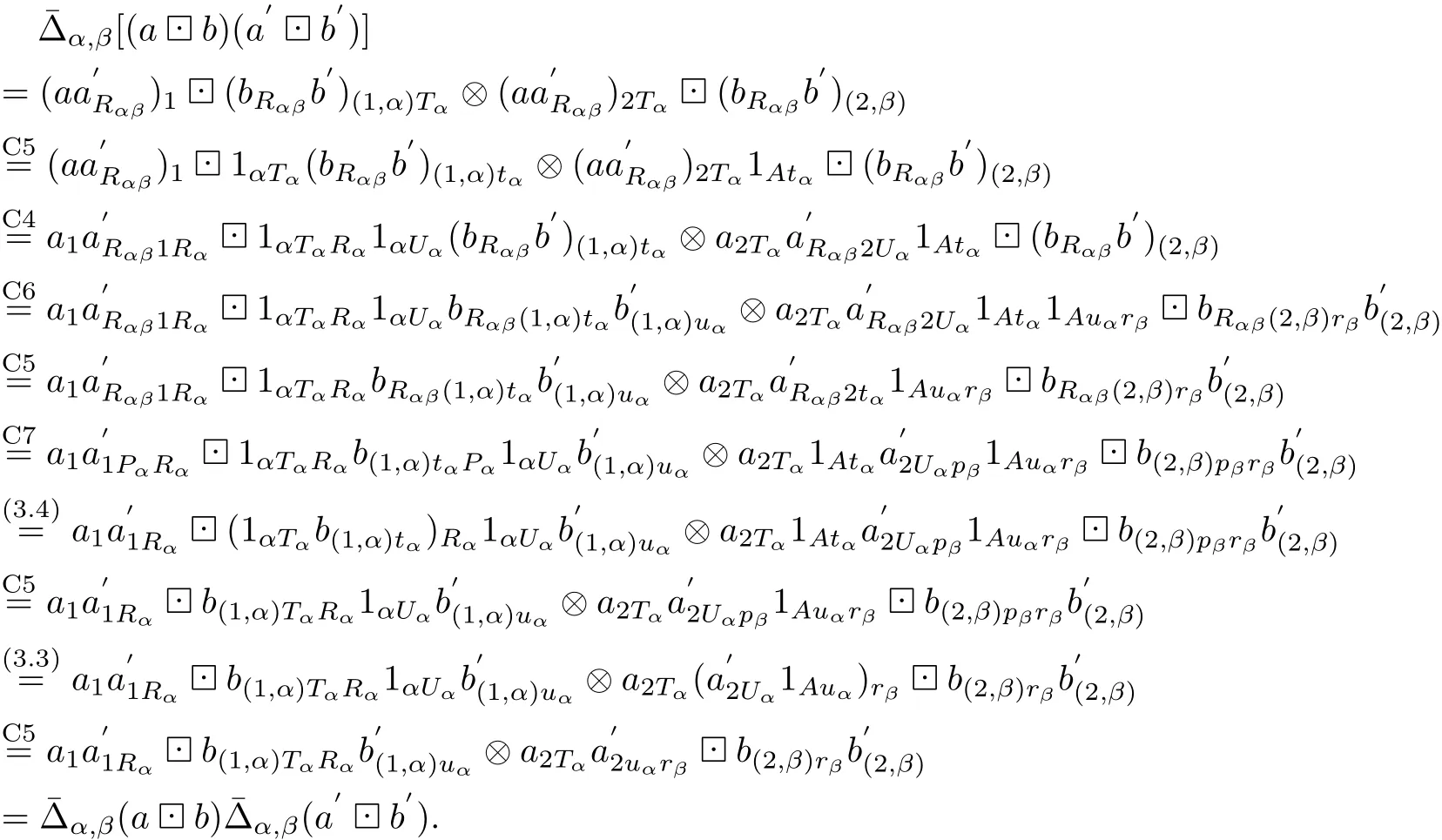
From the condition(C8),we get that¯ε is an algebra homomorphism.For all a∈A,b∈Beand α∈π,we compute

So we prove

Similarly,it follows that

Therefore,we conclude that(ATRB={ATRBα}α∈π,¯Δ,¯ε,¯S)is a Hopf π-coalgebra.

通过加强混凝土养生，可防止混凝土因内外温差而出现开裂情况。在完成混凝土浇筑施工后，须及时修整缓凝土裸露面，并对承台顶面的高程进行复核。待混凝土初凝后可采用双层土工布进行覆盖、洒水，时间至少14d，并安排专人负责，洒水的频率需结合每天的天气情况而定，但需确保土工布具有较大的湿度。

2)⇒1)Straightforward.

Corollary 3.1Let B be a Hopf π-coalgebra.Let A be both an algebra and a coalgebra (but not necessarily bialgebra).Suppose that A is a left π-B-comodule coalgebra.Then the following are equivalent

1)For all a,a′∈A and b∈Bαβ,the conditions(A1)∼(A5)below hold

2)(A#RB,¯Δ,¯ε,¯S)is a Hopf π-coalgebra with the multiplication,the coproduct¯Δ,the counit ¯ε and the antipode¯S given by

ProofLet the cotwisted map T be de fi ned by Tα(a⊗b)=a(−1,α)b⊗a(0,α),for any a∈A and b∈Bα.By Theorem 3.1,we can get the corollary.

Corollary 3.2Let B be a Hopf π-coalgebra.Let A be both an algebra and a coalgebra (but not necessarily bialgebra).Suppose that A is a left π-B-module algebra.Then the following are equivalent

1)(A×TB={A×TBα},={Δ¯α,β},ε¯,S¯={S¯α})is a Hopf π-coalgebra,where the multiplication,,ε¯eandS¯ are given as

2)The conditions(B1)∼(B7)hold

(B1)A×TB is a π-twisted tensor coproduct;

(B2)T(1A⊗1α)=1α⊗1A,Δ(1A)=1A⊗1A;

(B3)(aa′)1⊗1αTα⊗(aa′)2Tα=a1(1αTα(1.e)·a′1)⊗1αTα(2,α)1αtα⊗a2Tαa′2tα;

(B4)bTα⊗aTα=1αTαbtα⊗aTα1Atα,for all a∈A,b∈Bα;

(B5)(b(1,α)b′(1,α))Tα⊗1ATα⊗b(2,β)b′(2,β)=b(1,α)Tαb′(1,α)tα⊗1ATα(b(2,β)(1,e)·1Atα)⊗b(2,β)(2,β)b′(2,β),for all b,b′∈Bαβ;

(B6)(b(1,e)·a)1⊗b(2,αβ)(1,α)Tα⊗(b(1,e)·a)2Tα⊗b(2,αβ)(2,β)=(b(1,α)Tα(1,e)·a1)⊗b(1,α)Tα(2,α)1αtα⊗1ATα(b(2,β)(1,e)·a2tα)⊗b(2,β)(2,β),for all a∈A and b∈Bαβ;

(B7)(εA⊗ε)Re=ε⊗εAand εAis an algebra map. 3)The conditions(C1)∼(C5)hold

(C1)A×TB is a π-twisted tensor coproduct;

(C2)T(1A⊗1α)=1α⊗1A,Δ(1A)=1A⊗1A;

(C3)ΔA(a(b·a′))=a1(b(1,e)Te·a′1)⊗a2Te(b(2,e)·a′2),for all a,a′∈A and b∈Be;

(C4)(b(2,α)b′)Tα⊗(a(b(1,e)·a′))Tα=b(1,α)Tαb′tα⊗aTα(b(2,e)·a′tα),for all a,a′∈A and b,b′∈Bα;

(C5)For all a∈A and b∈Be,εA(b·a)=ε(b)εA(a)and εAis an algebra map.

ProofLet the twisted map R be de fi ned by Rα(b⊗a)=b(1,e)·a⊗b(2,α)for all a∈A and b∈Bα.By Theorem 3.1,it is obvious that 1)⇔2).

2)⇒3)We observe that,from(B3)and(B5),we have the following equations

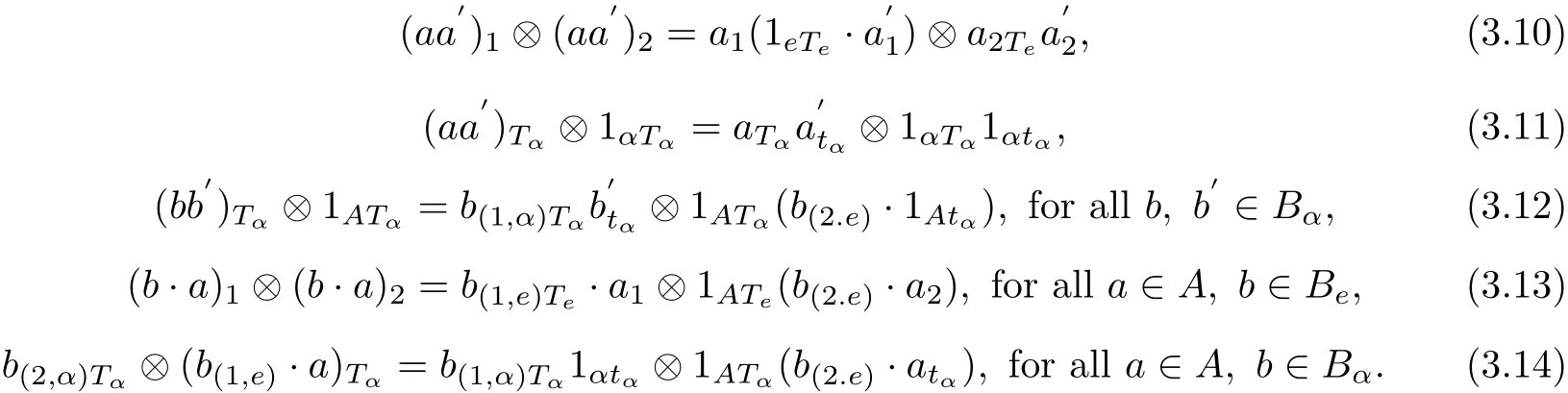
Now we compute

and so the condition(C3)is proved.Also,

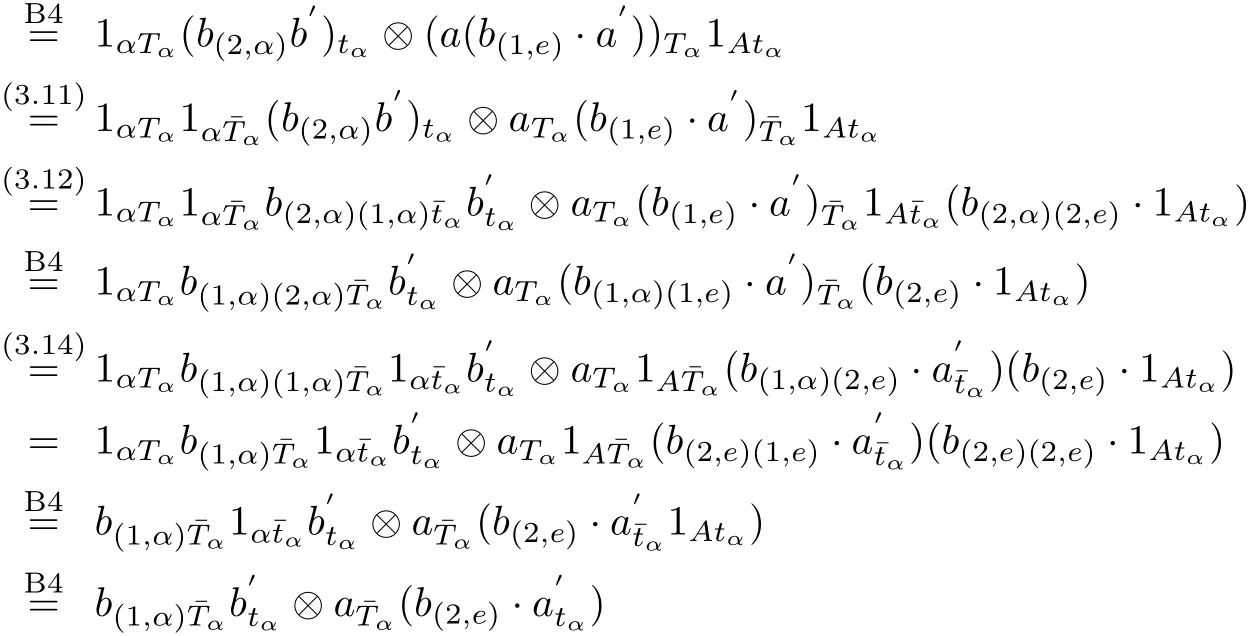
and so we get the condition(C4).

3)⇒2)It is easy to have equations(B4),(B5),Eqs(3.10),(3.11),(3.13)and

Next,we check(B6)as follows,for all b∈Bαβand a∈A,

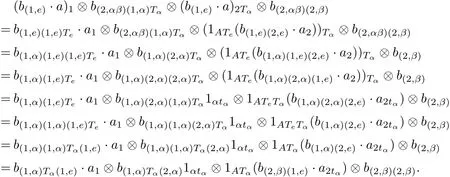
This completes the proof of the corollary.

[References]

[1]TURAEV V G.Homotopy Quantum Field Theory[M].Z¨urich:European Mathematical Society Pubishing House,2010:186-200.

[2]CAENEPEEL S,DE LOMBAERDE M.A categorical approach to Turaev’s Hopf group-coalgebras[J].Comm Algebra,2006,34(7):2631-2657.

[3]VIRELIZIER A.Hopf group-coalgebras[J].J Pure and Applied Algebra,2002,171:75-122.

[4]VIRELIZIER A.Graded quantum groups and quasitriangular Hopf group-coalgebras[J].Comm Algebra, 2005,33(9):3029-3050.

[5]WANG Shuan-hong.Group entwining structures and group coalgebra Galois extensions[J].Comm Algebra, 2004,32(9):3417-3436.

[6]WANG Shuan-hong.Group twisted samsh products and Doi-Hopf modules for T-coalgebras[J].Comm Algebra,2004,32(9):3437-3458.

[7]WANG Shuan-hong.Morita Contexts,π-Galois Extensions for Hopf π-coalgebras[J].Comm Algebra,2006, 34(2):521-546.

[8]ZUNINO M.Double construction for crossed Hopf coalgebra[J].J Algebra,2004,278:43-75.

[9]ZUNINO M.Yetter-Drinfeld modules for crossed structures[J].J Pure and Applied Algebra,2004,193: 313-343.

[10]CAENEPEEL S,ION B,MILITARU G,et al.The factorization problem and the smash biproduct of algebras and coalgebras[J].Algebra Represent Theory,2000,3:19-42.

[11]MA Tian-shui,WANG Shuan-hong.General double quantum groups[J].Comm Algebra,2010,38(2):645-672.

[12]RADFORD D E.The structure of Hopf algebra with a projection[J].J Algebra,1985,92:322-347.

tion:16W30

CLC number:O153.3Document code:A

1002–0462(2014)02–0274–09

date:2012-11-30

Supported by the Fund of the Key Disciplines of Xinjiang Uygur Autonomous Region (2012ZDXK03)

Biography:CHEN Quan-guo(1980-),male,native of Shangqiu,Henan,an associate professor of Yili Normal University,Ph.D.,engages in Hopf algebras.