On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables

WU Yong-feng

(Department of Mathematics and Computer Science,Tongling University,Tongling 244000,China; Center for Financial Engineering and School of Mathematical Sciences,Soochow University,Suzhou 215006,China)

On the Strong Laws for Weighted Sums of m-negatively Associated Random Variables

WU Yong-feng

(Department of Mathematics and Computer Science,Tongling University,Tongling 244000,China; Center for Financial Engineering and School of Mathematical Sciences,Soochow University,Suzhou 215006,China)

In this article,the author establishes the strong laws for linear statistics that are weighted sums of a m-negatively associated(m-NA)random sample.The obtained results extend and improve the result of Qiu and Yang in[1]to m-NA random variables.

Marcinkiewicz-Zygmund strong law;complete convergence;weighted sums; m-negatively associated random variable

§1.Introduction

The concept of negatively associated(NA)was introduced by Joag-Dev and Proschan[2].

Def i nition 1.1A f i nite family of random variables{Xk,1≤k≤n}is said to be NA if for any disjoint subsets A and B of{1,2,···,n}and any real coordinate-wise nondecreasing functions f on RAand g on RB,

whenever the covariance exists.An inf i nite family of random variables is NA if every f i nite subfamily is NA.

Hu et al[3]introduced the following concept of m-negatively associated(m-NA).

Def i nition 1.2Let m≥1 be a f i xed integer.A sequence of random variables{Xn,n≥1} is said to be m-NA if for any n≥2 and any i1,···,insuch that|ik−ij|≥m for all 1≤k/= j≤n,Xi1,···,Xinare NA.

We now provide two examples of sequences of m-NA random variables.

Example 1.1Let{Xn,n≥1}be a sequence of NA random variables and let m≥2. For n≥1,let r≥1 be such that(r−1)m+1≤n≤rm and let Zn=Xr.Then{Zn,n≥1} is a sequence of m-NA random variables.

Example 1.2Let{Xn,n≥1}be a sequence of NA random variables and let{Yij,i≥1,1≤j≤m−1}be an array of independent random variables which is independent of {Xn,n≥1}.Let m≥2.For n≥1,let r≥1 be such that(r−1)m+1≤n≤rm and let

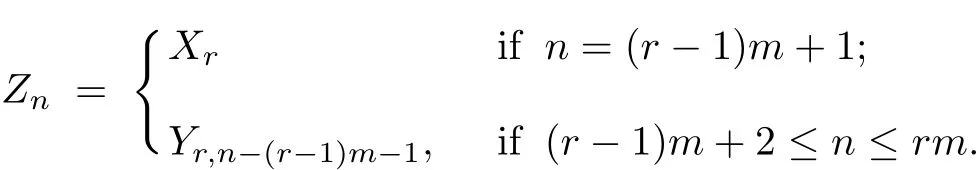
Then{Zn,n≥1}is a sequence of m-NA random variables.

Let{X,Xn,n≥1}be a sequence of random variables and{ani,1≤i≤n,n≥1}be a triangular array of constants.Because the weightedare very important in some linear statistics,the strong convergence for the weighted sums has been studied by many authors(see[1,4-12]).

The concept of the complete convergence was introduced by Hsu and Robbins[13].A sequence of random variables{Un,n≥1}is said to converge completely to a constant θ if

In view of the Borel-Cantelli lemma,the above result implies that Un→θ almost surely. Therefore,the complete convergence is a very important tool in establishing almost sure convergence of summation of random variables as well as weighted sums of random variables.

Recently Qiu and Yang[1]studied the following Marcinkiewicz-Zygmund strong law.

Theorem ASuppose 1/p=1/α+1/β for 1＜α,β＜∞and 1＜p＜2.Let{X,Xn,n≥1}be a sequence of NA random variables with indentical distributions,and let{ani,1≤i≤n,n≥1}be an array of constants satisfying

If E|X|β＜∞and EX=0,then

The purpose of this article is to establish the complete convergence and the Marcinkiewicz-Zygmund strong laws for linear statistics of m-NA sequences of random variables.The obtained results extend and improve the result of Qiu and Yang[1].It is worthy to point out that we obtain the complete convergence result for weighted sums of m-NA random variables under the same conditions of Qiu and Yang[1].

Throughout this paper,the symbol C represents positive constants whose values may change from one place to another.

§2.Preliminaries

A sequence of random variables{Xn,n≥1}is said to be stochastically dominated by a random variable X(write{Xn}≺X)if there exists a constant C＞0 such that

Lemma 2.1Nondecreasing functions def i ned on disjoint subsets of a set of m-NA random variables are m-NA.

Lemma 2.2[1416]Let{Xk,k≥1}be a sequence of NA random variables,EXk=0, E|Xk|q＜∞for some q≥2 and for every k≥1.Then there exists C=C(q)depending only on q,such that

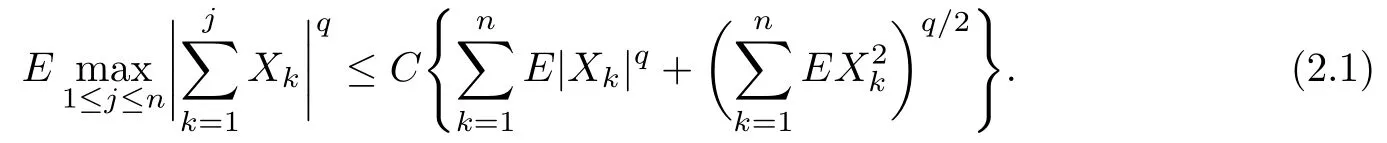
Lemma 2.3Let{Xk,k≥1}be a sequence of m-NA random variables,EXk=0, E|Xk|q＜∞for some q≥2 and for every k≥1.Then there exists C=C(q,m)depending only on q and m,such that(2.1)remains true.

ProofIf n≤m,obviously{Xn,n≥1}is a sequence of NA random variables.Therefore,Def i ne

Lemma 2.4Let{Xn,n≥1}be a sequence of random variables with{Xn}≺X.Then there exists a constant C such that,for all q＞0 and x＞0

(i)E|Xk|qI(|Xk|≤x)≤C{E|X|qI(|X|≤x)+xqP(|X|＞x)};

(ii)E|Xk|qI(|Xk|＞x)≤CE|X|qI(|X|＞x).

§3.Main Results

Theorem 3.1Suppose 1/p=1/α+1/β for 1＜α,β＜∞and 1＜p＜2.Let {Xn,n≥1}be a sequence of m-NA random variables with EXn=0 and{Xn}≺X and let {ani,1≤i≤n,n≥1}be an array of constants satisfying(1.1).If E|X|β＜∞,then

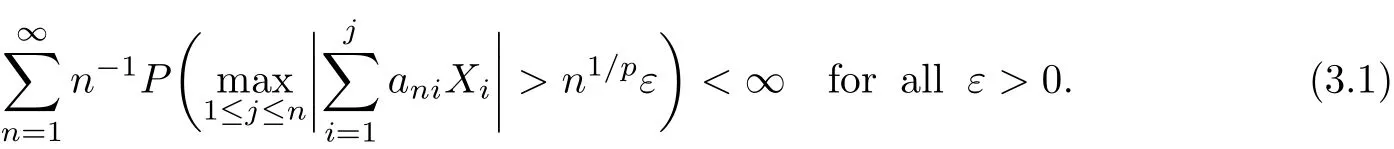
Corollary 3.1Under the conditions of Theorem 3.1,(1.2)holds.

Remark 3.1Corollary 3.1 generalizes the result of Qiu and Yang[1]to m-NA random variables.From the proof of Corollary 3.1,we will fi nd that(3.1)implies(1.2).Therefore, Theorem 3.1 extends and improves Theorem A.

Proof of Theorem 3.1Without loss of generality,we may assume that ani≥0.For fi xed n≥1,de fi ne

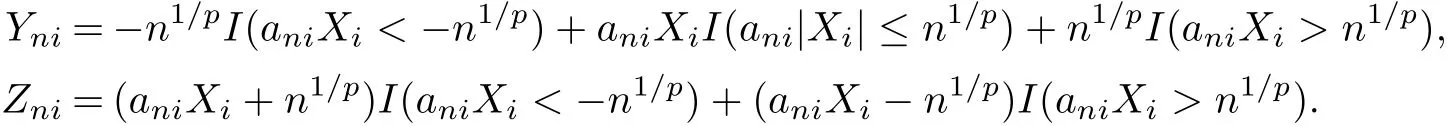
Then Yni+Zni=aniXiand{Yni,i≥1,n≥1}and{Zni,i≥1,n≥1}are both m-NA by Lemma 2.1.Then

From(1.1),without loss of generality,we may assume thatNoting that E|X|β＜Then by 1/p=1/α+1/β,we have

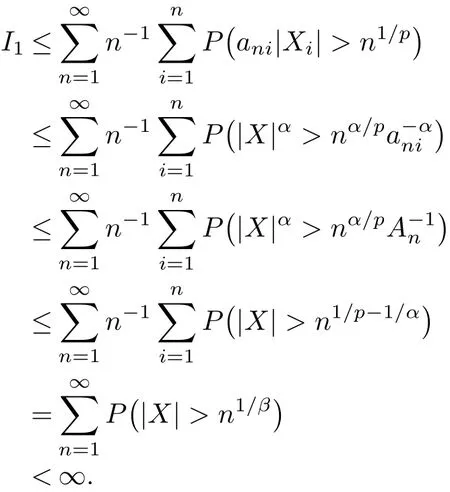
Next we prove I2＜∞.We f i rst show that

It is easily seen that|Zni|≤ani|Xi|I(ani|Xi|＞n1/p).By EXn=0,1/p=1/α+1/β and E|X|β＜∞,we get

From(3.2),it follows that while n is sufficiently large,＜n1/pε/2.Let q＞max{α,β,2}.Then by the Markov inequality and Lemma 2.3,it follows that

By Lemma 2.4,we have

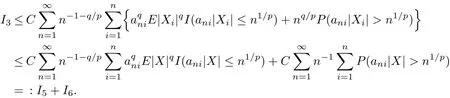
By a similar argument as in the proof of I1＜∞,we can get I6＜∞.Then we prove I5＜∞. If β≥α,by q＞β and(3.4),we have

If β＜α,by q＞β,β＞p and(3.3),we have

Then we prove I4＜∞.By Lemma 2.4 and q＞2,we have

Similar to the proof of I1＜∞,we have

Hence,while n is sufficiently large,＜1 holds.Thus by a similar argument as in the proof of I1＜∞,we can get

Finally we prove I7＜∞.From 1/p=1/α+1/β and 1＜p＜2,we know that α≤2 and β≤2 can not hold simultaneously.Hence we need only to consider the following three cases.

Case 1α＜2≤β.

By(3.4)and 1/p=1/α+1/β,we have

Case 2α≥2,β≥2.

By(3.3)and p＜2,we have

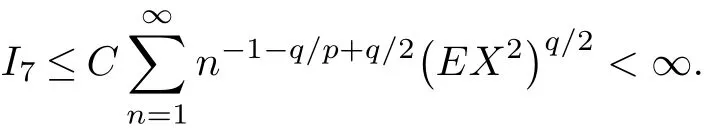
Case 3α≥2,1＜β＜2.

By(3.3)and β＞p,we have

The proof is completed.

By the Borel-Cantelli Lemma,we get

For all positive integers n,there exists a positive integer k0such that 2k0−1≤n＜2k0.By (3.5),we have

Hence,we prove that(1.2)holds.The proof is completed.

[References]

[1]QIU De-hua,YANG Xiang-qun.Strong laws of large numbers for weighted sums of identically distributed NA random variables[J].J Math Research Exposition,2006,26(4):778-784(in Chinese).

[2]JOAG D K,PROSCHAN F.Negative association of random variables with applications[J].Ann Statist, 1983,11(1):286-295.

[3]HU Yi-jun,MING Rui-xing,YANG Wen-quan.Large deviations and moderate deviations for m-negatively associated random variables[J].Acta Math Sci,2007,27B(4):886-896.

[4]CUZICK J.A strong law for weighted sums of i.i.d.random variables[J].J Theor Probab,1995,8(3): 625-641.

[5]WU Wei-biao.On the strong convergence of a weighted sum[J].Statist Probab Lett,1999,44(1):19-22.

[6]SUNG S H.Strong laws for weighted sums of i.i.d.random variables[J].Statist Probab Lett,2001,52(4): 413-419.

[7]CAI Guang-hui.Strong laws for weighted sums of NA random variables[J].Metrika,2008,68(3):323-331.

[8]WU Qun-ying.Complete convergence for weighted sums of sequences of negatively dependent random variables[J].J Probab Stat,2011,Article ID:202015.

[9]ZAREI H,JABBARI H.Complete convergence of weighted sums under negative dependence[J].Stat Papers, 2011,52(2):413-418.

[10]SUNG S H.On the strong convergence for weighted sums of random variables[J].Stat Papers,2011,52(2): 447-454.

[11]ZHOU Xin-cai,TAN Chang-chun,LIN Jin-guan.On the strong laws for weighted sums of ρ∗-mixing random variables[J].J Inequal Appl,doi:10.1155/2011/157816.

[12]SHEN Ai-ting.On the strong convergence rate for weighted sums of arrays of rowwise negatively orthant dependent random variables[J].Rev R Acad Cienc Exactas Fs Nat,Ser(A)Mat(RACSAM),doi:10.1007/s13398-012-0067-5.

[13]HSU P L,ROBBINS H.Complete convergence and the law of large numbers[J].Proc Nat Acad Sciences, 1947,33(2):25-31.

[14]SU Chun,ZHAO Lin-cheng,WANG Yue-bao.Moment inequalities and week convergence for negatively associated sequences[J].Sci China,1997,40A(2):172-182.

[15]SHAO Qi-man.A comparison theorem on maximum inequalities between negatively associated and independent random variables[J].J Theor Probab,2000,13(2):343-356.

[16]YANG Shan-chao.Moment inequalities for the partial sums of random variables[J].Sci China,2001,44A(1): 1-6.

tion:60F15

CLC number:O211.4Document code:A

1002–0462(2014)02–0265–09

date:2012-11-26

Supported by the Humanities and Social Sciences Foundation for the Youth Scholars of Ministry of Education of China(12YJCZH217);Supported by the Natural Science Foundation of Anhui Province(1308085MA03);Supported by the Key Natural Science Foundation of Educational Committe of Anhui Province(KJ2014A255)

Biography:WU Yong-feng(1977-),male,native of Zhongyang,Anhui,an associate professor of Tongling University,M.S.D.,engages in probability limit theory.