滚动轴承的MSE和PNN故障诊断方法
2014-07-27熊国良周继慧
陈 慧,张 磊,熊国良,周继慧
(华东交通大学 机电工程学院,南昌330013)
滚动轴承的MSE和PNN故障诊断方法
陈 慧,张 磊,熊国良,周继慧
(华东交通大学 机电工程学院,南昌330013)
针对滚动轴承不同运行状态振动信号具有不同复杂性的特点,提出一种新的基于多尺度熵(multiscale entropy,MSE)和概率神经网络(probabilistic neural networks,PNN)的滚动轴承故障诊断方法。该方法首先利用MSE方法对滚动轴承振动信号进行特征提取,并将其作为PNN神经网络的输入,再利用PNN自动识别轴承故障类型及故障程度。实验数据包括不同故障类型和不同故障程度样本,结果表明,相比于小波包分解和PNN结合的诊断方法,提出的方法具有更高的诊断精度,能有效实现滚动轴承故障类型及程度的诊断。
振动与波;多尺度熵;概率神经网络;滚动轴承;故障诊断
滚动轴承广泛应用于各类机械设备,起着承受载荷和传递载荷的作用且工作环境恶劣,是机器中最易损坏的零件之一。据统计,在旋转机械的各种故障中,滚动轴承故障约占40%[1,2]。因此有效进行滚动轴承故障诊断具有重要的现实意义,也是近年来国内外机械故障诊断技术的重点。
振动信号是轴承故障信息的载体,滚动轴承故障诊断的关键是从振动信号中提取特征信息。滚动轴承振动信号特别是存在故障时表现出非线性、非平稳特点,因此有效提取相应的非线性非平稳特征是滚动轴承故障诊断关键[3]。随着非线性科学理论的发展,小波分解、近似熵以及样本熵等众多非线性方法和参数已被广泛地应用于机械设备故障诊断领域。相比于小波变换,小波包分解(wavelet packet transform,WPT)不仅对信号的低频部分进行分解,还对信号的高频部分分解,但如果环境噪声过大,小波包分解的效果并不理想[4];而近似熵和样本熵等非线性参数只能反映时间序列在单一尺度上的信息[5,6]。对于振动信号而言,不同的故障类型及不同的故障程度,其信号复杂程度不同,熵值也不同。多尺度熵(muItiscale entropy,MSE)在不同尺度下衡量信号的复杂性[7],可以表征不同故障类型及不同故障程度下轴承动态信号的跨尺度复杂性。因此,MSE可以作为故障特征参数。
鉴于滚动轴承振动信号特别是故障发生时存在的非线性特点以及对轴承故障自动诊断的现实需求,本文提出一种基于MSE和概率神经网络(probabilistic neural networks,PNN)的滚动轴承故障智能诊断方法,并利用实验数据对其诊断性能进行检验。
1 多尺度熵(MSE)
Richman等于2000年提出了样本熵(sample entropy,Samp En)概念并用于度量时间序列复杂性[6],但是Samp En只反映时间序列在单一尺度上的信息。Costa等在Samp En的基础上,提出了MSE用来反映时间序列在不同尺度下的自相似性和复杂性程度。
MSE是基于Samp En的一种时间序列复杂性度量方法。给定长度为N的原始数据Xi={x1,x2,…,xN},其MSE计算步骤如下[7,8]:
(1)粗粒化(coarse-graining)处理。预先给定嵌入维数m和相似容限r,建立新的粗粒向量(coarse grained vector)

τ=(1,2,…,τmax)为正整数,称为尺度因子。尺度τ=1对应的时间序列{y(1)}是原始时间序列。
(2)计算Samp En值。对于尺度τ下的粗粒化子序列{y1(τ),y2(τ),…,yM(τ)},M为子序列长度,其Samp En计算步骤如下[6]:
①给定模式维数m,由原序列组成m维数矢量

式中,i=1,2,…,M-m。
②定义Y(i)与Y(j)之间的距离

③定阈值r,对于每一个i值统计d(i,j)<r的数目(称为模板匹配数)及此数目与距离总数M-m-1的比值,记作Bim(r)
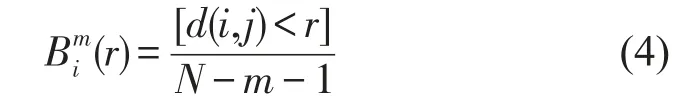
其中1≤j≤N-m,j≠i,求其对所有i的平均值

④再对m+1重复①~③步,得到Bm+1(r);
⑤理论上,此序列的样本熵为

当N取有限值时,取SampEn估计值为
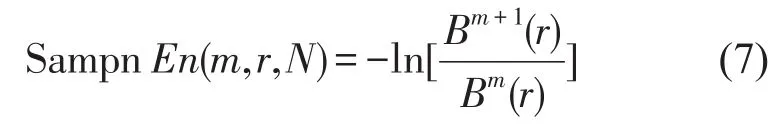
利用式(2)~(7)可计算每一个尺度子序列的Samp En,得到MSE

显然,多尺度熵与尺度因子τ,嵌入维数m和相似维数r这三个参数有关。
2 概率神经网络(PNN)
概率神经网络是D.F.Specht博士于1989年首次提出的一种基于Bayes分类规则和Parzen窗的用于概率密度函数估计的并行算法。PNN结构简单、训练简洁、是应用广泛的一种人工神经网络[9]。在解决分类问题时,其优势是在保持非线性算法的高精度等特性同时以线性学习算法来完成非线性学习算法所做的工作。PNN模型由输入层、模式层、求和层以及输出层组成,基本结构如图1所示。

图1 概率神经网络基本结构图
输入层接收来自训练样本的值,将特征向量传递给网络,其神经元数目和故障特征向量的维数相等。模式层神经元的个数等于各个类别训练样本数之和,其每个模式单元的输出为

式中Wi为输入层与模式层连接权值;δ为平滑因子。
求和层累计样本属于某类的概率,按式(9)计算得到故障模式的概率密度函数估计。输出层神经元是一种竞争神经元,每个神经元分别对应于一个故障类型。
基于PNN神经网络的故障诊断方法可描述为[10]:假设有两种已知的故障模式θA、θB,对于要判断的故障特征样本X=(x1,x2,…,xn):
若hAlAfA(X)>hBlBfB(X),则X∈θA;
若hAlAfA(X)<hBlBfB(X),则X∈θB;
式中hA、hB为故障模式θA和θB的先验概率(hA=NA/ N,hB=NB/N),NA、NB为故障模式θA、θB的训练样本数;N为训练样本总数;lA为将属于θA的故障特征样本X错误地划分到模式θB的代价因子;lB为将本属于θB的故障特征样本X错误地划分到模式θA的代价因子;fA、fB为故障模式θA、θB的概率密度函数(probability density function,PDF),通常PDF不能精确获得,只能根据现有的故障特征样本求其统计值。
Parzen于1962年提出了一种从已知随机样本中估计概率密度函数的方法,估计式如下

式中Xai为故障模式θA的第i个训练向量;m为故障模式θA的训练样本数目;δ为平滑参数,其取值确定了以样本点为中心的钟状曲线的宽度。
3 基于MSE和PNN的智能诊断模型
本文提出的滚动轴承智能故障诊断模型如图2所示,模型分为训练和测试两个步骤。首先从历史数据库或通过试验方式获取各类轴承状态的振动信号样本并提取信号的MSE作为特征向量,用于训练PNN网络。对于后续测取的未知故障类型样本振动信号,提取MSE特征向量后输入到训练好的PNN,便能进行滚动轴承运行状态的自动识别。

图2 基于MSE和PNN的智能诊断模型
4 实验过程
4.1 滚动轴承实验数据
滚动轴承实验数据来自美国Case Western Reserve大学轴承数据中心[11]。如图3所示的试验台由左边功率为1.49 kw的三相感应电机,右边的测功机以及中间连接两者的力矩传感器和联轴节组成。实验轴承为6205深沟球轴承,安装在电机右侧驱动端用于支撑电机轴。通过电火花加工人为制造故障的方式总共模拟了七种轴承状态,包括不同故障类型以及相同故障类型但故障程度不同等情况。表1给出了故障类型和故障程度的具体情况,其中故障程度由(故障直径×故障深度)表示。本文通过MSE特征提取和PNN模式识别进行上述七种轴承状态的自动识别。

图3 滚动轴承故障试验台
实验过程电机转速为1 750 r/min,采样频12 000 Hz,每个样本长度2 000点,各轴承状态采集到60个样本。七种轴承状态的振动信号时域波形如图4所示,可发现不同轴承状态的信号很难区分,因此有必要进行特征提取。

图4 轴承故障信号图

表1 实验数据情况
4.2 滚动轴承MSE特征提取
利用模式识别方法进行轴承故障智能诊断的前提是从动态信号中提取能够有效反映轴承状态信息的特征量。MSE能够挖掘动态信号多尺度上的非线性信息,这也是将其用于轴承故障特征提取的出发点。根据参考文献中的总结[6,7],本文计算MSE时取相似容限r=0.15×SD(SD是原始数据的标准差),m=2,τ=10。对上述滚动轴承的七种不同状态信号,随机取一组MSE如图5所示。从图中可以看出,正常轴承信号的多尺度熵在大部分尺度上较大,而其它故障状态的MSE随着尺度因子的增加而递减。说明无故障状态下振动信号自相似性比故障状态下要高,即无故障状态下振动信号的复杂度更大。显然,滚动轴承各状态下的细节特征通过不同尺度下的Samp En值得到体现,能更好的揭示轴承不同状态故障特征。

图5 滚动轴承7种状态信号的多尺度熵
4.3 MSE+PNN故障诊断效果
每种轴承状态各随机取40组样本用于训练,得到一个40×7=280大小的训练样本集。以训练集训练好PNN网络之后,将未用于训练的20×7=140组样本用于测试分类器的诊断性能。图6和图7分别给出了PNN网络在训练集和测试集上的识别效果。在训练集上,准确率为100%。而在测试集上,仅有一个属于C7(外圈故障)的样本被误诊为C5(内圈故障)。可见,所提出的基于MSE特征提取的滚动轴承PNN网络智能诊断模型能以较高的精度实现轴承状态识别。

图6 MSE+PNN训练效果
4.4 与小波包(WPT)能量特征提取方法对比

图7 MSE+PNN测试效果
为了验证MSE特征提取方法在非线性信息提取方面的优势,本节利用WPT进行轴承振动信号特征提取,再以PNN分类结果衡量WPT特征提取效果。对滚动轴承原始信号进行3层小波包分解(小波基函数为db 3),提取第三层8个频率成分归一化能量作为特征向量[3]。相应地,PNN网络的输入层神经元节点个数为8,输出层神经元节点个数为7,对应于轴承的七种状态。同样从各轴承状态随机抽取40×7=280组信号组成训练集用于PNN网络训练,剩余的140组信号作为测试样本。基于WPT能量特征提取的分类结果如图8所示,分类错误同样发生在C7状态,有一个C7样本误识为C6,三个错误分类为C5。
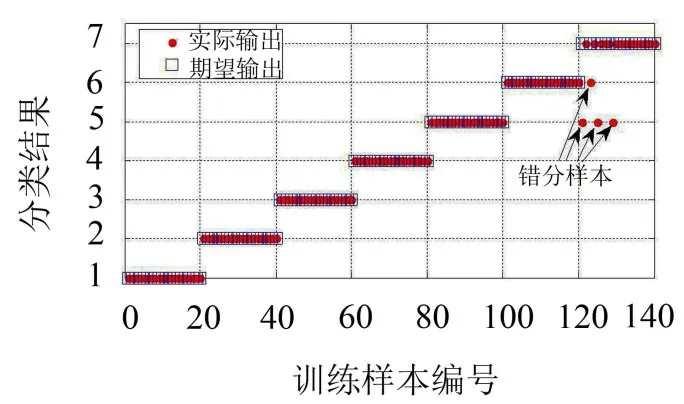
图8 WPT+PNN测试效果
两种特征提取方法的诊断效果比较如表2所示,MSE和WPT特征提取的错误识别都发生在状态C7。但是MSE方法的结果优于WPT,并且对每一类轴承的诊断预测结果比较均衡。

表2 两种特征提取方法对比
5 结语
本文提出了一种基于多尺度熵(MSE)和概率神经网络(PNN)的滚动轴承故障诊断方法。MSE能够有效地从多尺度框架下提取轴承振动信号的非线性特征信息,PNN具有结构简单、学习速度快和识别精度高等优点。实验结果表明,所提出的基于多尺度熵特征提取的滚动轴承故障概率神经网络诊断模型能够以较高地精度识别包含不同故障类型和不同故障程度的轴承运行状态。与小波包特征提取方法的比较结果表明MSE能够以其非线性信息挖掘能力提取到更多的轴承振动信号特征信息。
[1]杨伟新,江亲瑜,王珍,等.EMD与高阶累积量在滚动轴承故障诊断中的应用[J].噪声与振动控制,2011(05):142-145.
[2]佟雨燕,陆森林.信号相关性和EEMD-Hilbert包络在滚动轴承故障诊断中的应用[J].噪声与振动控制,2013,33 (05):144-149.
[3]夏均忠,苏涛,马宗坡,等.基于EMD的滚动轴承故障特征提取方法[J].噪声与振动控制,2013(02):123-127.
[4]张辉,王淑娟,张青森,等.基于小波包变换的滚动轴承故障诊断方法的研究[J].振动与冲击,2004,23(04):127-130.
[5]Pincuss M.Approximate entropy as a measure of system complexity[J].Proc Natl Sci USA,1991(88)∶2297-2301.
[6]Richman J S,Moorman J R.Physiological time series analysis using approximate entropy and sample entropy [J].AmericanJournalofPhysiology-Heartand Circulatory Physiology,2000,278(6)∶H2039-H2094.
[7]Costa M,Goldberger A L,Peng C K.Multiscale entropy analysis of biological signals[J].Physical Review E,2005 (71)∶1-18.
[8]Costa M,Goldberger A L,Peng C K.Multiscale entropy analysis of complex physiologic time series[J].Physical Review Letter,2002,89(6)∶1-18.
[9]Specht D F.Probabilistic neural networks[J].Neural Networks,1990,3(1)∶109-118.
[10]李冬辉,刘浩.基于概率神经网络的故障诊断方法及应用[J].系统工程与电子技术,2004(07):997-999.
[11]Case Western Reserve University.Bearing data center.[EB/OL].http∶//cse groups.case.edu/bearingdatacenter/ pages/welcome-case-western-reserve-university-bearingdata-center-website.2013-12-20.
Fault Diagnosis of Rolling Bearings Using MSE and PNN
CHENHui,ZHANGLei,XIONG Guo-liang,ZHOU Ji-hui
(School of Mechatronics Engineering,East China Jiaotong University,Nanchang 330013,China)
∶Considering different levels of complexity of vibration signals of rolling bearings in different operating conditions,a novel fault diagnosis method has been proposed based on the multiscale entropy(MSE)and probabilistic neural networks(PNN).Fault feature vector is firstly extracted from the vibration signals using MSE and then provided to PNN neural network as the input.The PNN network will identify the bearing fault type and severity level simultaneously.The experimental data are collected from an induction motor bearing involving various fault types and severity levels.The results demonstrate that the proposed method has a higher accuracy in rolling bearing fault diagnosis than the method of the combination of wavelet packet decomposition with PNN.
∶vibration and wave;multiscale entropy;PNN;rolling bearing;fault diagnosis
TH165+.3;TN911.7;TH18< class="emphasis_bold">文献标识码:ADOI编码:
10.3969/j.issn.1006-1335.2014.06.038
1006-1355(2014)06-0169-05
2014-04-21
国家自然科学基金资助项目(51205130、51265010);
江西省教育厅科技项目(GJJ12318);
江西省自然科学基金项目(20132BAB216029)
张磊(1989-),男,湖北孝感人,硕士研究生,主要研究方向:工程信号处理与机械故障诊断。
熊国良,男,博士生导师。
E-mail∶lzhang0712@126.com
